基于动态MIC优化TCN的混凝土坝变形预测模型研究

曾 欣，马 力，戴子卿

(1.水利部水利水电规划设计总院，北京 100120；2.南京市水利规划设计院股份有限公司，江苏 南京 210022；3.中国人民解放军总医院第六医学中心，北京 100037)

0 引 言

水库大坝的结构健康监测一直为国内外学者研究的热点内容之一。由于结构健康监测(Structural health monitoring，SHM)属于多学科交叉领域，涉及大量传感器或仪器自动监测结构对荷载的响应情况，根据采集得到的数据对结构健康进行诊断[1]。SHM的核心部分就是数据，包括数据采集、异常数据处理、数据挖掘和数据建模等方面的相关算法和应用[2]。近年来，随着大型水利工程监测系统与数据科学发展，SHM系统已经广泛应用于水利工程领域。水利工程SHM系统的应用算法经历了3个阶段，从传统回归算法[3]、机器学习算法[4-5]到目前的深度学习算法[6]。其中混凝土大坝作为水工结构中重要的组成部分，大坝的安全始终影响着上下游人民的生命财产、社会的经济的安全[7]。为了监控混凝土大坝的安全，通过大坝的变形、温度、渗流、应力等指标进行监测，其中大坝变形是混凝土大坝安全重要的控制和评价指标。由于大坝变形与影响因子间为非线性关系，前人已经通过各种数学算法模型进行研究预测大坝变形，并得到了工程运用。为了处理变量间映射的非线性问题，人工神经网络[8](Artificial neural network，ANN)应运而生。其发展最初基于数学和阈值逻辑算法[9-10]，神经网络模型的训练拟合过程实质是通过相关学习算法不断逼进损失函数极小值的超高维度的非线性函数拟合过程。目前，神经网络依据不同的研究对象已经发展出多种网络构型[11-12]。其中对于监测、检测数据的分析，卷积神经网络(Convolutional neural network，CNN)的应用最为广泛，包括医学[13]、机械工业[14]、土木工程[15]、教育[16]等领域。在处理大坝变形的离散时间序列的神经网络中，一维CNN适应性较好。而一维CNN由于卷积核的限制，对于数据较大的数据库的处理能力不足，容易出于收敛不稳定和数据爆炸的问题。为了解决上述CNN的存在问题，本文对CNN的因果卷积、膨胀卷积进行约束与残差链接操作而建立时间卷积网络样本训练预测模型。

由于混凝土大坝的变形对外部条件变化的反馈不可能即刻完成，该过程需有一定的时间并且属于复杂的非线性过程。为了实现混凝土大坝变形的因变量与环境量的自变量之间在时序关系上刻画，采用动态MIC进行研究计算。其中MIC在研究水利工程的水位荷载与工程性态的相关性已经得到了较好地应用，如孟庆筱等[17]运用MIC算法研究了三峡蓄水进程中库首区地震活动与库水位的关联性；黄观文等[18]结合MIC算法分析了降雨和库水位与滑坡变形的时滞性并进行了滑坡变形的预测。为解决混凝土坝变形的时滞性问题并提高变形预测的精度，本文提出基于动态MIC优化的时域卷积神经网络的混凝土坝位移预测模型。首先通过动态MIC确定变量间的最佳时滞时间；以环境量因子构建的矩阵作为输入，目标向量为大坝变形测点的变形量，建立时间卷积网络的变形时序模型。并且采用均方根误差、拟合优度和平均绝对百分比误差等指标评价模型的精度和可靠度，以此评价大坝变形的变化趋势。

1 模型理论

1.1 时间卷积神经网络

由前文可知，卷积神经网络CNN是人工神经网络的一种。人工神经网络简称神经网络(neural network，NN)是一种模仿生物神经网络结构和功能的数学模型或计算模型，其本质还是搜寻一种线性空间与非线性空间之间的映射关系的拟合过程[19]，神经网络的求解结构如图1所示。人工神经网络本质是解决两类问题——分类和回归问题。

卷积神经网络求解结构的核心在于“卷”和“积”。如果求解维度是多维的，则网络的卷积计算是一个积分过程，即

(1)

式中，f为网络的表征函数；g为网络的卷积核。

一般地，大坝位移测点为时间序列，属于离散函数，需要进行积分退化处理，求解网络为

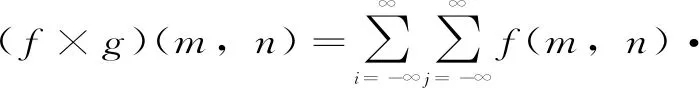
(2)

卷积神经网络中的卷积核又称过滤器(filter)，是按照给定规则随机初始化，然后经过训练得到的。在模型训练过程中，为了提高运算层面上的效率，训练得出的正向存储的过滤器便可以看作是已经翻转的卷积核。卷积算子较卷积网络模型中的卷积操作多了一步对“卷积核”的反转操作，神经网络中的卷积运算其核心是一种互相关运算，而并非严格数学意义上的卷积操作，如图2所示。

对于离散的大坝变形时间序列，1D CNN较之标准CNN的精度更高，其中1D CNN输入矩阵以及卷积核的维度为1，所以更适合用于序列问题的解决，1D CNN具体的卷积操作如图3所示。由于1D CNN受到卷积核尺寸的限制，相对于循环神经网络解决时序数据的能力就显得不足。

为了突破卷积核尺寸的限制，时间卷积网络在普通1D CNN基础上，进行严格时间约束的因果卷积膨胀卷积与残差链接操作，TCN结构如图4所示。该网络可以较好地捕捉数据时序上的前后依赖关系，强化了卷积结构处理时序数据建模任务的能力；在不损失信息的情况下，能够以层数的指数级扩大处理信息的能力。

1.2 时滞相关性

在混凝土大坝的变形监测中，大坝变形与其影响因子存在一定时滞性。准确捕捉时滞时间，可以进一步提高TCN模型训练样本的精度。由于MIC的广泛性和均匀性使之较MI等能够更准确检测两个变量间的线性、非线性或非函数关系，避免产生误导性结论，所以MIC能够覆盖所有的函数关系且无须对数据分布做任何假设。并且只要两变量之间存在某种映射关系，则它们的理论MIC值为1。但MIC只能度量序列时域上对应的数据，对存在多个影响因子的时间序列类型的映射关系的能力可能不强。所以采用时滞互相关的分析思路，将监测序列进行平移处理，计算输入序列和输出序列间的动态MIC值[20]，即

f(t)=fMIC({(x1，y1+t)，…，(xi，yi+t)，…(xN-t，yN)})

(3)

式中，t为滞后步数；X=(x1，x2，…，xN)为样本输入层；Y=(y1，y2，…，yN)为样本输出层，并且两者为等间隔监测序列。

为了保证时序数据样本在模型训练和测试过程中的统一性，采用滑动窗口方式构建，选择特定窗口时长，然后以固定步长滑动，每一个窗口的数据作为模型的训练或测试的一个样本。从而可以得到变形与影响因子间的时滞关系曲线，由关系曲线则可以确实最佳时滞时间。

1.3 模型性能评价指标

为了定量的评价MIC-TCN预测模型的拟合及预测精度，采用评价数学模型常用的3种误差评价指标，分别为均方根误差RMSE(Root Mean Square Error)、拟合优度R(Correlation Coefficient)和平均绝对百分比误差MAPE(Mean Absolute Percentage Error)。RMSE用来表示实测值与计算值之间的偏差，表征计算值的离散程度，如式(4)。R是量化模型拟合值和预测值与实测值之间统计关系的系数，如式(5)。MAPE用来评价计算结果的相对误差，如式(6)。由式(4)～(6)可知，变形预测模型的性能越好，精度越高，则RMSE、MAPE和R的值越小。

(4)

(5)

(6)

2 模型结构及实现步骤

Smith等[21]建议为了提高样本数据的利用率，同时使用较少类型的层次以保持网络简洁，避免在重复卷积池化过程中丢失某些重要特征。因此，在TCN网络的层与层之间本文采用1×1卷积，具体TCN网络结构模型的示意如图5所示。

根据样本的具体情况，确定TCN网络结构的层次和类型之后，则可进行混凝土大坝变形预测模型的构建。基于MIC-TCN的混凝土大坝变形预测模型如6所示。具体步骤为①通过动态MIC，计算训练样本的输入层自变量和输出层因变量之间的动态相关关系，确定环境量(输入层)和位移(输出层)之间的滞后关系。②利用TCN学习拟合训练样本环境量和位移的映射关系，即变形网络模型。③根据变形网络模型，输入预测样本的环境量，得到位移的预测值。④将模型的预测值与实测值进行对比，分析误差，评价模型的精度。

3 案例应用

3.1 工程概况

本文选择某水电站大坝的变形作为研究对象，通过训练模型的结构参数，不断逼近影响因子空间与效应量空间之间的最佳映射关系，将影响因子空间映射到高维的非线性空间，然后再映射到效应量空间上。考虑到数据完整性和代表性，选择2013-01-01～2016-12-31期间的坝体某条倒垂线测点的水平顺河向位移监测数据与环境量监测数据，其中2013-01-01～2015-12-31为训练测试集，2016-01-01～2016-12-31为位移预测集。图7为该变形测点以及库水位和日降雨量的监测时序，位移的正负代表方向。由图7可知，在库水位周期调度和季节性降雨情况下，测点位移出现了较明显的变化，雨季位移正向增加，旱季位移负向增加，并且库水位的调度也会影响位移的变化。

由于该坝体测点是每隔1～2 d的自动化监测，因此数据存在缺失值，直接建模会增大结果误差，因此在构建模型前，采用3阶样条插值法对变形量数据进行升采样处理，重采样结果较原数据量增加约130%。为避免插值和去噪过程对预测结果造成的影响，及时更新模型的输入样本空间，而对测试集未预测样本不进行数据预处理，并采用实际监测日数据与测试样本输出进行对比分析。

由于序列数据在时间上的前后相关性，本文选择文献[22]提出的时间序列预测模型的滚动原点交叉验证(GROE，generalized rolling origin evaluation cross-validation)方法来优化模型参数。根据文献[23]，本文设置GROE交叉验证方法的折数p=5，预测步数H根据模型为单步或多步预测具体设置，最后将5个模型的输出向量平均化处理，以作为该模型结构的最终输出。

3.2 输入时序变量长度的确定

采用动态MIC计算了大坝变形与水位变量之间的时滞关系，关系曲线如图8所示。由图8可知，水位与大坝变形具有很高的相关性，随着时间的增加(前期)，MIC相关性越高，相关性最大的为20 d处，说明大坝变形的变化对水位的反馈具有时滞性。滞后天数在20 d后，相关度开始下降，该大坝的水位最佳滞后时间为20 d。

确定最佳滞后天数，则可以确定TCN模型的视野域的输入序列长度为20 d。序列的输入长度采用滑动时窗方法构建模型样本空间，便于后续模型调参与优化。

3.3 结果与分析

先后输入该坝的监测点的训练样本及预测样本，经过MIC-TCN变形预测模型学习训练及预测计算，则可得到该坝的位移拟合及预测结果，其中2013-01-01～2015-12-31为位移拟合结果，2016-01-01～2016-12-31为位移预测结果，如图9所示。动态MIC-TCN变形预测模型的位移拟合精度如表1所示。由图9和表1可知，动态MIC-TCN变形预测模型具有较高的学习拟合能力和精度。

表1 拟合精度评价指标值

为了更好地评判MIC-TCN大坝变形预测模型地好坏，本文还通过差分自回归滑动平均模型(ARIMA)预测了该坝的位移情况，两者预测的结果如图10所示，两者的误差分析如表2所示。

表2 ARIMA模型与TCN模型预测精度评价指标表

由图5和表2可知，ARIMA和MIC-TCN两个模型在预测反映大坝变形的趋势上都有较好的精度。但在反映和影响大坝性态的测点突跳点的位移预测方面，ARIMA模型没有MIC-TCN模型的预测精度高，并且在RMSE、R2和MAPE的3个误差分析指标上，MIC-TCN模型都好于ARIMA模型。说明基于动态MIC-TCN大坝变形预测模型的整体预测能力较强。

4 结 论

本文基于动态MIC-TCN模型构建了混凝土坝变形预测模型，可以得到以下结论：

(1)通过动态MIC可以计算分析大坝变形与影响因子间的时滞关系，并能确定最佳时滞时间；TCN神经网络可以对大坝测点的样本进行学习训练以及拟合预测，能够适用于大样本的情形。

(2)由案例应用可知，MIC-TCN变形预测模型的拟合及预测精度较高，较之常规ARIMA模型具有更高的训练预测能力，能够较好地预测混凝土大坝的变形情况。说明MIC-TCN变形预测模型具有较高的工程使用价值。

(3)神经网络模型结构往往存在独一性，当处理新任务时，需要重新训练模型结构，效率不高，因此考虑通过迁移学习(Transfer Learning)，将一个训练好的不同特征空间上映射关系进行一定的算子变换，然后应用于类似的任务上。