基于卡尔曼滤波的STFT域回声抵消算法

刘 杨，杨飞然,3，梁兆杰，杨 军,3

(1.中国科学院声学研究所，北京 100190；2.中国科学院大学，北京 100049；3.中科新声（苏州）科技有限公司，江苏 苏州 215163；4.深圳供电局有限公司，广东 深圳 518000)

0 引言

受到新冠疫情全球大流行的影响，在线会议系统得到了快速的发展，语音通信是该系统的核心功能。声音也是人工智能与物联网融合时代最关键的入口之一。近年来，人机交互技术在自动导航系统、智能音箱、语音遥控电视机等一系列产品中获得成功应用。回声抵消是语音通信和人机交互的关键问题之一[1-2]。上述这些技术的快速发展拓展了回声抵消的应用场景并对回声抵消提出了更高的要求。

自适应滤波是回声抵消问题最成熟的解决方案。该方法通过辨识扬声器到近端传声器之间的回声路径来估计近端传声器采集到的回声信号，再用传声器信号减去估计的回声信号得到误差信号，即需要的近端语音信号。声学回声路径通常需要利用几千阶的FIR滤波器来进行建模，因而算法的计算复杂度是首先需要考虑的问题之一。目前，频域自适应滤波算法是声学回声抵消的标准解决方案[3-4]。约束的频域自适应滤波算法利用快速傅里叶变换(Fast Fourier Transformation,FFT)来实现精确的线性卷积和线性相关操作[2]，因而相比直接在时域实现具有更低的复杂度。

还有一类回声抵消方法是在短时傅里叶变换域(Short Time Fourier Transformation,STFT)直接进行的。与上述基于线性卷积的方法不同，短时傅里叶变换域的算法实现的一般不是一个精确的线性卷积[5]，而只是一个逼近的方法。早期的算法[6-10]首先估计出回声信号的功率谱再利用语音增强中常用的维纳滤波来完成回声抑制，但这些算法都忽略了相位信息，因而得到的近端语音质量较差。最近发展的一类算法[11-14]同时估计回声信号的幅度和相位信息，因而近端语音质量得到了保证。文献[11]和[13]的算法没有讨论在双端对讲状态下滤波器的更新问题。文献[12]和[14]的算法分别直接采用卡尔曼滤波和递归最小二乘(Recursive Least Squares,RLS)在每一个频点进行滤波器系数更新，因而复杂度较高。

本文研究了短时傅里叶变换域的单通道线性回声抵消问题。首先给出了标准的卡尔曼滤波更新方程，讨论了过程噪声和观测噪声的估计方法，进一步给出了简化的卡尔曼滤波算法来降低计算复杂度。本文另一个贡献是引入了远端信号更多的临近频点来进一步提高回声抵消的性能。最后通过实验验证了所提算法的有效性。

1 模型

考虑如图1所示的单通道回声抵消模型，传声器接收到的信号可以表示为

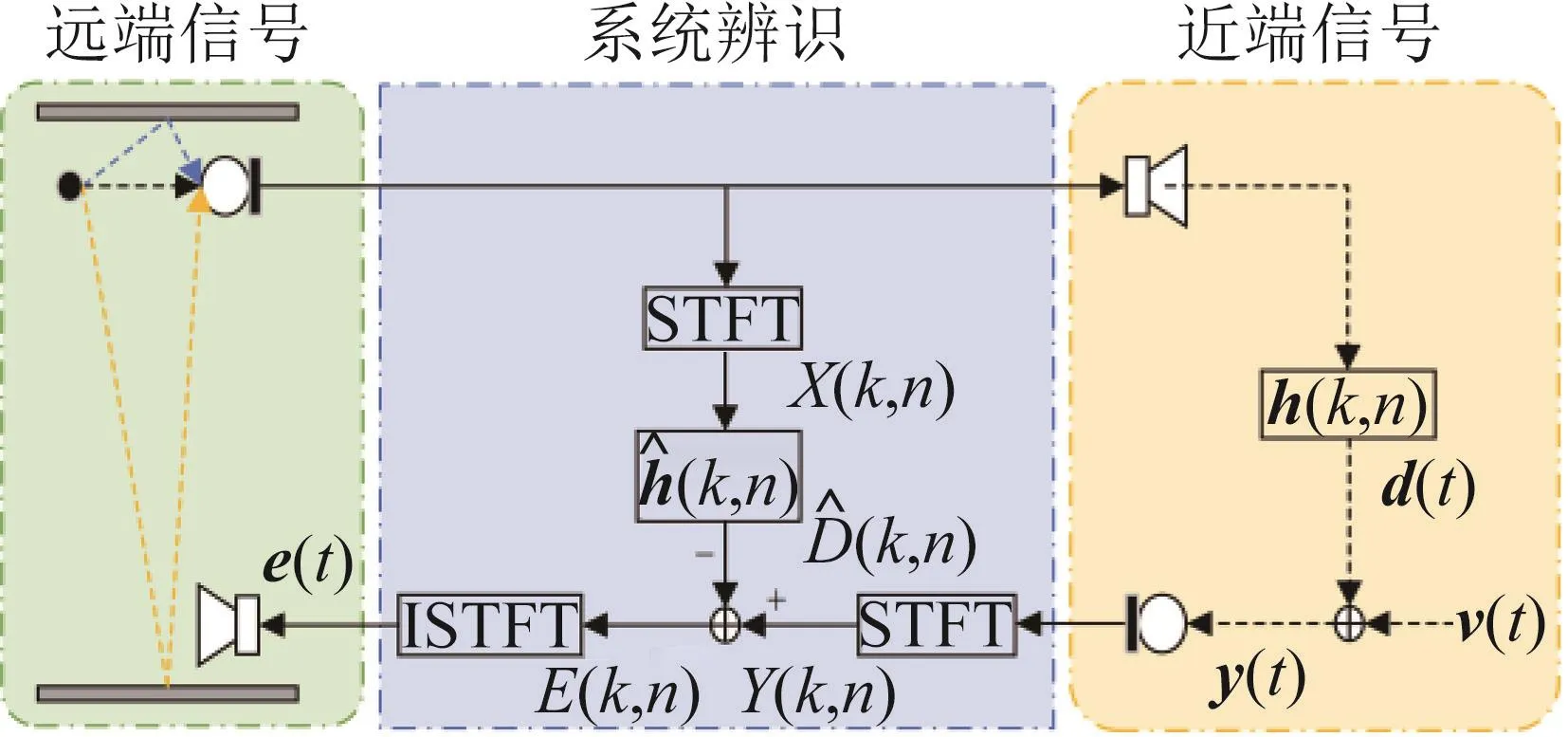
图1 单通道回声抵消模型Fig.1 Single-channel echo cancellation model

其中：回声信号d(t)=h(t)*x(t)是远端参考信号x(t)通过扬声器到传声器的回声路径h(t)后得到的，v(t)包括近端语音s(t)和噪声信号n(t)。传声器接收信号在STFT域可表示为

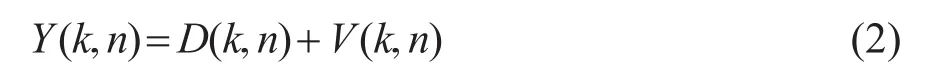
其中：Y(k，n)、D(k，n)和V(k，n)分别表示第n个时间帧和第k个频点的传声器信号、回声信号和近端信号。在STFT域的回声信号可以表示为[14-15]

其中：X(k，n)是第n个时间帧和第k个频率块的远端参考信号，H(k，k＇，l)为频点k和k＇之间的交叉子带滤波器系数，N为傅里叶变换窗长。

直接使用式(3)进行计算复杂度较高，因而是不现实的。下面我们给出几种近似的实现方法。假设STFT分析窗的频率分辨率足够高，则各频率之间信号相互独立，即当 k≠k＇时，H(k，k＇，l)=0。当k=k＇时，可以将H(k，k＇，l)重写为第n个时间帧和第k个频点的第l个时延块的回声路径Hl(k，n)。随着l的增加，Hl(k，n)的值随时延块的衰减越来越快，因而可以只保留L个系数对STFT域回声信号进行近似。从而，STFT域的回声信号可以近似表示为

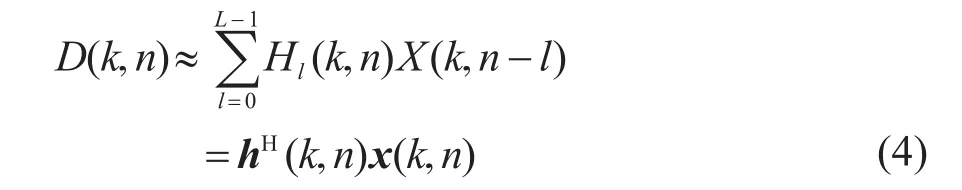
其中：h(k，n)=[H0(k，n)...HL-1(k，n)]T为滤波器系数向量，x(k，n)=[X(k，n)...X(k，n-L+1)]T为输入信号向量。

在实际应用中，STFT分析窗的频率分辨率可能不足以使 k≠k＇时的H(k，k＇，l)=0。此时引进相邻时间帧和频率帧的信息，可以进一步提高算法的回声抵消量[10]。如图2所示是扩充邻近频点信息的两种方式。第一种扩充的远端参考信号向量x(1)(k，n)表示为

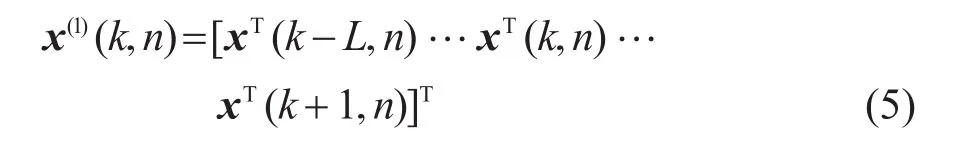
式(5)使用L个时间帧以及每个时间帧当前频点上下各K个频率帧的信息，向量长度为(2K+1)L。第二种扩充的远端参考信号向量x(2)(k，n)表示为

式(6)使用L个时间帧以及当前时频点上下各K个频率帧的信息，向量长度变为L+2K，图2中的箭头是向量元素的填充顺序。远端信号向量进行扩充之后，每个时频点对应的回声路径向量h(k，n)的长度也扩充成相应的长度。

图2 邻近频率帧信息扩充类型Fig.2 Expansion types of adjacent frequency frame information

假设估计的第n个时间帧，第k个频率块的房间回声路径系数向量为，则估计的频域回声信号为

从而可以得到估计的频域近端信号：

2 STFT域卡尔曼滤波

2.1 状态方程和观测方程

在回声抵消问题中，实际要估计的是房间回声路径的频域系数向量h(k，n)。本文采用一阶马尔可夫模型对回声路径的变化进行建模：

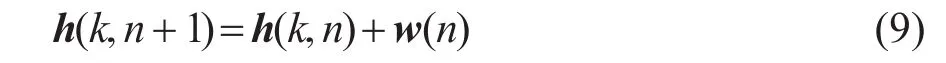
其中：w(n)是体现回声路径变化的状态噪声。假设w(n)服从0均值高斯分布，状态噪声的协方差矩阵为Φw(k，n)=E[w(n)wH(n)]。

利用式(4)，得到STFT域观测方程的表达式：

2.2 卡尔曼滤波器的更新过程

在卡尔曼滤波中，状态向量估计误差的协方差矩阵为

最小化目标函数(11)，得到卡尔曼滤波器的更新过程为[15]

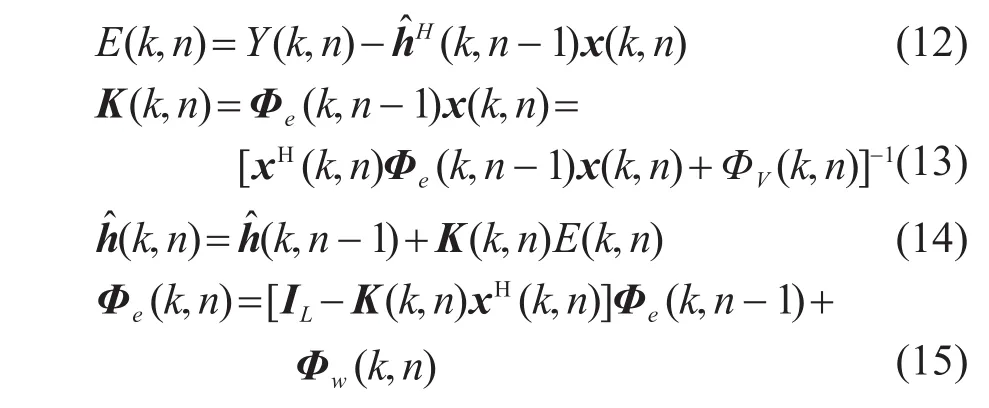
其中：K(k，n)是卡尔曼增益。

2.3 状态噪声和观测噪声的估计

状态噪声协方差Φw(k，n)估计的准确性影响到系统对通道变化的跟踪能力和算法的稳态性能。我们假设w(n)的各个元素之间互不相关，则Φw(k，n)变为对角矩阵 Φw(k，n)=φw(k，n)I。利用下式估计φw(k，n)：

其中：参数c的值越大，算法的稳态收敛误差越小，跟踪能力越差，反之亦然。

观测噪声协方差ΦV(k，n)的估计准确性影响到系统的双端对讲性能。当系统达到稳态时，误差信号近似为近端信号，因而可以直接利用误差信号来估计观测噪声方差：

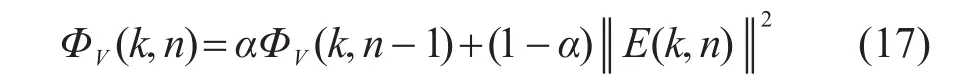
其中：α是遗忘因子。

2.4 低复杂度实现

为了简化卡尔曼滤波的计算复杂度，首先将误差协方差矩阵 Φe(k，n)简化为对角矩阵 Φe(k，n)≈φe(k，n)IL[16]。则卡尔曼增益的更新公式变为[16]

低复杂度STFT域卡尔曼滤波器(Low Complexity STFT-Kalman,LC-STFT-Kalman)更新时，按顺序更新式(12)、(19)、(14)、(20)，其中状态噪声协方差的估计仍然采用式(16)和(17)。

3 计算复杂度

表1列出了STFT域的归一化最小均方误差[11](STFT-NLMS)、STFT-RLS[14]、变步长分块频域自适应滤波[4](VS-PBFDAF)、STFT-Kalman和LC-STFT Kalman5种算法更新每个采样点所需的乘法数。

表1 各算法更新每个采样点所需的乘法数Table 1 Numbers of multiplications required for each output of different algorithms

设定用于估计回声路径的滤波器长度为M，STFT域算法的FFT点数为N，重叠率为R∈[0，1]，即每次帧移N(1-R)个采样点，每个时频点估计的滤波器长度为P=M/[ ]N(1-R)。VS-PBFDAF算法的FFT点数为N，重叠率为50%，即每次帧移N/2点，则主滤波器块数为B=2M/N，阴影滤波器块数为Bb=B/2。已知计算所需要的乘法次数N点FFT(IFFT)所需实数乘法次数为Nlog2N、复数乘法为实数乘法的4倍、开方运算为实数乘法的40倍、除法运算为实数乘法的20倍。

图3给出了5种算法更新每个采样点所需的乘法次数随滤波器长度M的变化，其中短时傅里叶变换点数N=512，重合率R=75%。从图中可以看出，STFT-Kalman和STFT-RLS更新一个采样点所需的乘法次数随着回声路径的长度增加的趋势比其他三种算法快很多，其原因是这两种算法的计算量与每个时频点的滤波器长度的平方成正比。LCSTFT-Kalman的计算量比STFT-NLMS算法大，但比VS-PBFDAF小。

图3 5种算法更新每个采样点所需乘法次数随M的变化Fig.3 The numbers of multiplications required for each output of different algorithms as a function of filter length M

4 实验结果和分析

为了区分回声和近端语音，把TIMIT数据集中截取的英文作为远端信号，汉语普通话识别句表[17]中截取的中文作为近端信号。每段信号的总长度为40 s，采样率为16 kHz。如图4所示，远端信号为持续干净语音，近端信号在20～30 s出现语音，在近端传声器接收信号中加入白噪声，信噪比(Signal to Noise Ratio,SNR)为30 dB。在生成回声时，回声路径采用实际录制的房间脉冲响应并截断至2048点。在混合近端传声器接收信号时，近端信号与回声信号之比(Signal to Echo Ratio,SER)为0 dB。STFT的帧重合率为75%，分析窗和合成窗都采用汉宁窗。采用回声往返损耗增强(Echo Return Loss Enhancement,ERLE)对回声抵消算法的性能进行评估，其计算方法为

图4 实验采用的远端和近端信号Fig.4 Far-end and near-end signals used in the experiment

但ERLE仅能评估回声抵消量，无法体现通过算法后的近端语音失真程度，因此采用感知语音质量评价[18](Perceptual Evaluation of Speech Quality,PESQ)对回声抵消算法收敛后在双讲阶段的性能进行评估。状态转移因子c∈(0，1]，越接近1，算法的稳态收敛误差越小，收敛后的回声抵消性能越好。本文中采用c=0.999 992和α=0.8，状态噪声协方差和观测噪声方差的初值分别为Φw(k，0)=φw(k，0)I=0.05I和ΦV(k，0)=0.05。

图5比较了不扩充邻近频点的卡尔曼滤波算法、STFT-RLS[14]和VS-PBFDAF[6]的性能。设SNR为30 dB，SER为0 dB，将STFT-Kalman和LCSTFT-Kalman的参数都设置成N=512、L=16。STFT-RLS的傅里叶变换点数为512，每个时频点的滤波器长度为16，重叠率为75%。VS-PBFDAF估计的时域滤波器长度为2 048，分成4块，每个子滤波器的长度为512。从图5可以看出，基于STFT域的3种算法都比传统的VS-PBFDAF算法具有更快的收敛速度，这主要是由于前者在每个频点需要更新的系数较少。算法达到稳态后，VS-PBFDAF的ERLE最大，简化后的卡尔曼滤波算法LC-STFT Kalman比原来的精确实现形式性能有所下降。STFT-RLS、 STFT-Kalman、 LC-STFT-Kalman 和VS-PBFDAF等4种算法更新每个采样点所需的乘法数目分别为5 732、4 776、744、1 028。

图5 4种不同算法的回声往返损耗增强(ERLE)随时间变化曲线Fig.5 Variations of ERLE with time for different algorithms

图6比较了不同的远端频段扩充方式对回声抵消性能ERLE的影响。图6(a)为N=512，L=16的LC-STFT-Kalman算法的ERLE与扩充方式、扩充频点数的关系。从收敛速度来看，第一种扩充(type1)随着扩充频点的增加收敛速度明显变慢，第二种扩充(type2)对收敛速度的影响不大。这是由于采用第一种扩充方式后每个频点需要更新的滤波器系数明显增加。从算法收敛后的ERLE来看，第一种扩充收敛后的回声抵消量整体比未扩充时的高，K=1时效果最好。第二种扩充对回声抵消量的增加并不明显。图6(b)为N=2 048,L=4的LC-STFT Kalman算法的ERLE与扩充方式、扩充频点数的关系，其收敛规律与图6(a)相同。

图6 扩充频点对ERLE的影响Fig.6 Influence of expanded frequency points on ERLE

表2中给出了各算法收敛后双讲阶段的PESQ。对比表2和图5，VS-PBFDAF因其回声抵消量最大，且收敛后对语音的损伤最小，在双讲阶段的PESQ是最大的。LC-STFT-Kalman使用第一种扩充的PESQ更高，且N=2 048，L=4时的双讲稳定性比N=512，L=16时好，算法的PSEQ整体更高。

表2 各算法双讲阶段的感知语音质量评价(PSEQ)对比Table 2 Comparison of PESQ in the double-talk phase of the algorithms

表3给出了不同扩充方式和不同邻近频点数K对算法计算复杂度的影响。从表3中可以看出，N=512，L=16的组合要比N=2 048，L=4的计算复杂度高很多。同一种组合中，在上下扩充频点数K相同时，第二种扩充方式滤波器长度增加比第一种方式要少得多，因而其计算复杂度也小很多。

表3 更新单个采样点的计算复杂度随扩充方式和K的变化Table 3 Variation of the computational complexity of updating a single sample point with expansion mode and K

5 结论

本文提出了用于单通道回声抵消的STFT域的卡尔曼滤波算法，并给出了其快速实现方法。本文还在简化模型的基础上应用两种扩充临近频点提高回声抵消性能的方式，使得扩充频点后的简化卡尔曼滤波算法的回声抵消量性能有了显著提升。使用K=1的第一种扩充频点方式，可以使得LC-STFTKalman的回声抵消量达到40 dB，比精确实现的STFT-Kalman高5 dB。所提算法不需要双讲检测，具有比传统的频域自适应滤波算法更低的复杂度和更快的收敛速度，在很多场景下均具有较好应用前景。