变刚度曲筋结构表征和等几何分析与智能设计研究

郝 鹏，张坤鹏，王 博，王 群，石玉红

（1. 大连理工大学工业装备结构分析国家重点实验室，大连，116024；2. 辽宁省工业装备数字孪生重点实验室，大连，116024；3. 北京宇航系统工程研究所，北京，100076）

0 引 言

加筋薄壁结构由蒙皮和筋条组成，具有较高的比刚度和比强度，常用作航天运载器的主要承力结构，约占舱段干重的80%以上[1]。在传统的薄壁结构设计中，多为材料分布均匀的直线型常刚度加筋构型，如正置正交、等三角、Kagome加筋等。然而，直线构型本身就可视为对结构布局的强制约束，致使设计空间严重受限。同时，这种具有单一力学性能的常刚度设计，难以满足新一代装备的轻质高承载设计需求。

作为一种极具潜力的新型承力结构，国外学者[2～4]最近提出了整体型曲线加筋壁板的设计概念。采用电子束自由成形技术、激光精密金属沉积工艺、3D打印等技术可以选择性地沉积材料[2]，即结构从下至上“生长”，如图1a所示。这种新型结构最早由Kapania教授团队开展系统研究[3,4]，表明曲线加筋设计可调控无限小直筋的方向、间距、位置等特征，提供更大的设计空间。在与NASA兰利研究中心和洛克希德·马丁公司联合设计中，制造了曲线加筋的平板样件（见图1c）[3]，试验证明此类结构的承载优势。

图1 曲筋的制造和试验 Fig.1 Manufacture and Experimentation of Curvilinear Stiffener

相较于直筋，曲筋带有更复杂的结构特征，目前研究尚未形成统一的表征形式。Slemp等[3]采用NURBS函数描述曲线加筋路径。王丹等利用角度线性变化函数[5]和流线函数[6]定义曲线加筋路径。根据结构的开口类型，郝鹏等分别利用幂指数函数[7]和贝塞尔函数[8]表征曲线加筋路径。除了加筋路径，加筋布局和截面形貌的改变同样能够实现薄壁结构的变刚度设计[9]。郝鹏等[11]借助PCHIP函数对加筋非均匀布局和截面形貌进行统一表征。近年来，基于拓扑优化设计理念，形成一系列新颖的曲筋构型。张卫红[12]提出了一种加筋设计新方法：几何背景网格法，实现了三维曲面薄壁结构的加筋设计。王博等[13]为拓扑优化过程加入Helmholtz各向异性过滤约束，对异形喷管结构进行曲筋增强设计，并基于渐进均匀化技术提出了曲筋生成式方法[14]。褚晟等[15]利用水平集函数开展曲筋布局和形状的同步优化。李威等[16]根据结构主应力线直接生成曲筋路径。

曲线加筋结构给现有的数值分析方法带来了巨大挑战。与传统加筋构型不同，曲线筋条具有变曲率几何特征，无法实现自动结构化网格划分，且难以保证筋条与蒙皮网格共节点，这对于以多项式有限元方法为基础的商业软件来说，分析效率和精度都受到极大的限制。因此开发精度、效率更高的数值方法，对曲线加筋结构的设计具有重要的意义。Kapania等[17]使用插值算法来实现筋条单元和壳体单元自由度之间的耦合，该算法首先在无网格分析[18]中实现，进一步扩展到标准有限元分析[19]和等几何分析[20]。Saeedi等[21]使用相同的耦合方法，研究了不同参数对加筋板屈曲和弯曲行为的影响，如弯曲刚度、相对质量、横截面和筋条形状。郝鹏等[22]提出了一种NURBS样条加筋单元，针对曲线加筋结构中NURBS投影算法收敛困难的问题，对传统的投影算法进行了改进，改进的方法具有更高的鲁棒性，此外，基于筋条样条单元的加筋结构等几何分析方法在精度和效率方面均领先于有限元商业软件。

与传统直线加筋构型相比，复杂曲筋结构的梯度难以直接求解，王丹等[5]利用有限差分法获得结构的灵敏度信息，进一步结合移动渐近线方法开展曲筋路径的优化设计。为避免陷入局部最优解，郝鹏等[8]利用多岛遗传算法对开口筒壳进行了曲筋补强设计，并开展了复杂曲线网格加筋结构路径、布局及截面形貌的协同设计[11]。近年来，为了降低数值计算成本，数据驱动的代理模型和深度学习智能优化方法迅速发展。Li等[23]提出了图像驱动的板料成形智能优化算法，可节省90%的成形时间。Singh等[24]搭建了预测曲筋结构屈曲响应的深度神经网络，显著提升了结构优化效率。

复杂曲筋的高精度高效设计需要分别从分析模型和优化算法这两个方面入手。Kapania等[17]针对曲筋建立了高精度的壳单元分析模型，通过多项式代理模型[2]减少优化中的数值分析次数，并为NASA开发了曲筋专用设计软件EBF3PanelOpt[4]，考虑到过多设计变量对优化效率的影响，建议最多优化曲筋数目为6条。郝鹏等[22]建立了基于新型样条加筋单元和几何投影算法的曲筋结构等几何分析方法，并利用深度学习模型提出了曲筋布局的智能设计方法[10]，开发了结构变刚度智能设计优化软件平台，突破了传统设计参数优化的维度局限，可实现几十根曲筋的同步设计。

为推动变刚度曲线加筋结构在工程中的进一步应用，分别从该类结构的表征、等几何分析、优化层面对相关文献进行了梳理，对各方法的特点与适用性展开讨论，并总结了研究面临的挑战及未来发展趋势。

1 变刚度曲线加筋结构的表征

相较常刚度结构，设计变刚度曲线加筋结构的核心在于引入更丰富的结构特征。表1为曲线加筋结构的表征[11]，本章将分别对曲线加筋结构几何显式和隐式表征进行介绍。

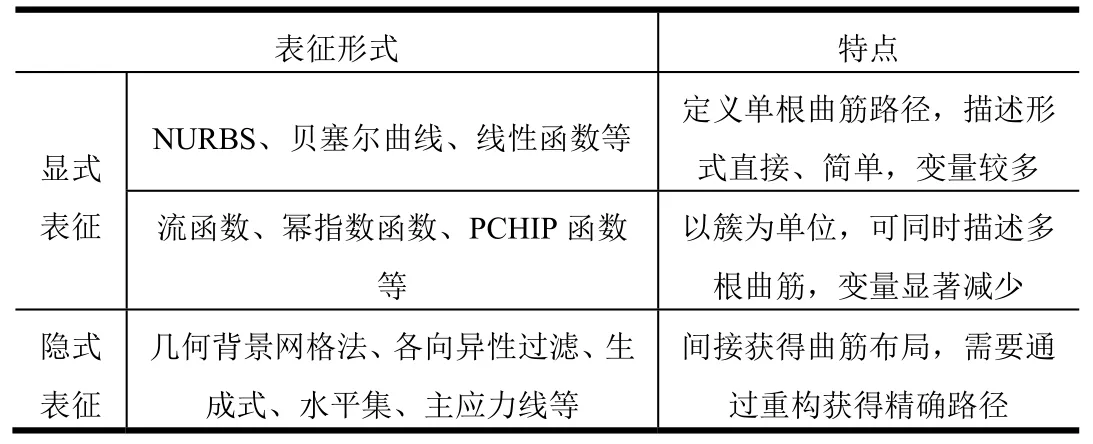
表1 曲线加筋结构的表征 Tab.1 Characterization of Curvilinearly Stiffened Structures

1.1 曲线加筋结构的显式表征

a）贝塞尔曲线：样条函数是表征曲线的最直接方式[8]。该函数由3个控制点控制，起点Ps，中点Pm，终点Pe。在归一化的设计空间中，曲筋路径被定义为

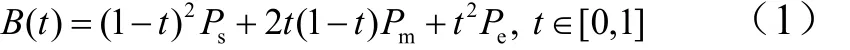
b）NURBS曲线：作为更加复杂的样条函数，Slemp等[3]利用NURBS函数对曲筋路径进行表征：

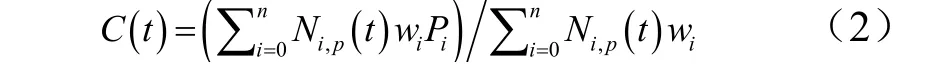
式中Ni,p为非周期节点矢量上的p次B样条基函数；Pi为控制点；wi为控制点的权因子。因此，可以通过控制点位置和权因子的变化，实现比贝塞尔曲线更为精确的曲筋路径控制。

c）线性函数：基于曲筋路径角度线性变化函数，王丹等[5]在长为l的方形设计区域中，定义一条通过原点的参考路径：

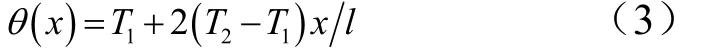
式中θ为路径的夹角；T1和T2分别为在路径起点和终点处的角度，如图2a所示。

d）流函数：利用描述流体运动的流函数，王丹等[6]在整个设计区域中定义了多根筋条路径的布局：

通过c的改变可以获得不同的流场。在流场中，将相同函数值的点进行投影，获得清晰的流线加筋路径，并且在同一流场中的路径彼此不相交。

e）幂指数函数：对于更加复杂的网格加筋壁板，通过幂指数函数的变化可以调控整体曲线加筋布局[7]。如图2b所示，曲筋的起点和终点沿矩形设计域边界移动，曲筋的中点位置由幂指数函数控制：

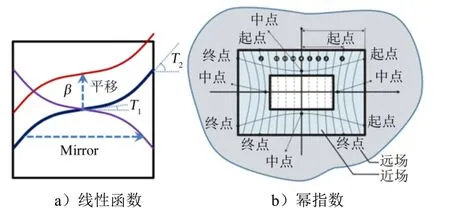
图2 线性函数和幂指数函数的表征 Fig.2 Characterization of Power Function and Linear Function

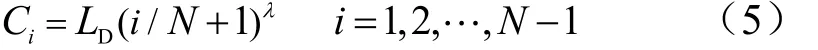
式中λ为布局参数；N为筋条数目；DL为设计域宽度。当λ=1时，路径间距相等；当λ＞1时，设计域中部的筋条比两侧更密集；当λ＜1时，情况相反。

f）PCHIP函数：针对多根筋条的位置分布特征，刘大川等[11]基于PCHIP函数提出了非均匀布局的调控方法。通过将参考路径移动不同距离di，获得含有N根筋条的一簇曲筋结构，表示为数组［d1,d2,…,dN］：

式中dmax和dmin分别为平移最大和最小距离。在坐标系中，直线表示筋条的均匀分布，当直线变为曲线时，筋条分布变为非均匀。图3为5种典型加筋布局[11]。

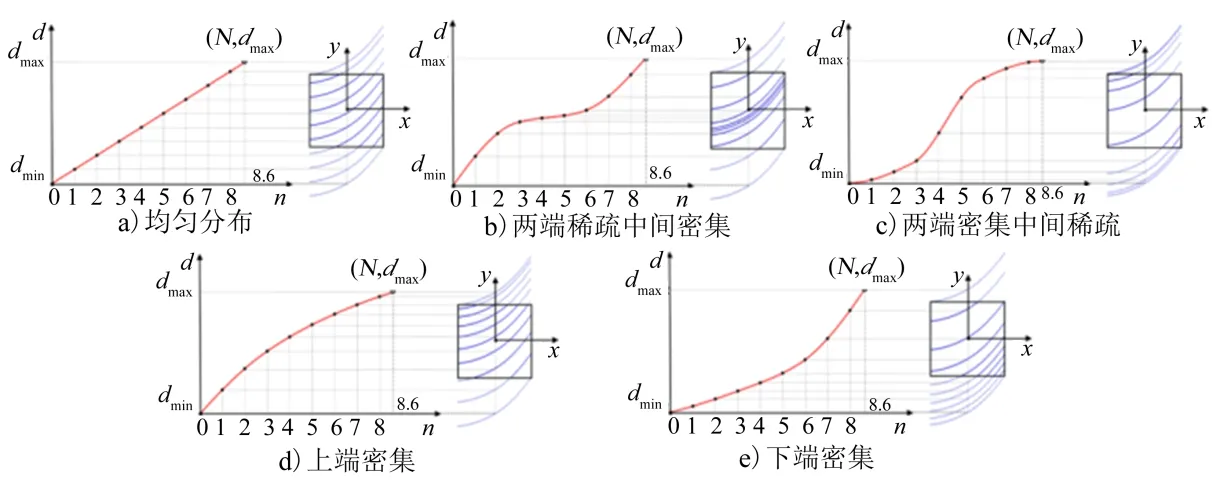
图3 曲线加筋布局的PCHIP表征 Fig.3 Curvilinearly Stiffened Layouts Characterized by PCHIP

1.2 曲线加筋结构的隐式表征

a）基于Helmholtz各向异性过滤的拓扑优化：基于结构拓扑优化设计理念，王博等[13]利用隐式Helmholtz偏微分方程定义了各向异性滤波器：

式中ρ为区域 Ω设计变量；ρ为过滤后的密度；c为三维基向量。在拓扑优化过程中，通过施加各向异性的过滤挤压约束，获得垂直于异形喷管曲面的加筋结构。

b） 基于渐进均匀化方法的曲筋生成式方法：马祥涛等[14]基于渐进均匀化技术提出了曲线加筋的生成式方法。首先定义了不同方向加筋单元，并利用等效方法获得各向异性的材料，再对材料分布进行拓扑优化，最后通过流线函数重构获得清晰的曲线加筋路径。

c）基于主应力线的曲筋布局方法：针对含有任意曲面的复杂壳体结构，李威等[16]提出基于主应力线的曲筋布局方法。如图4所示，根据主应力场获取多条初始加筋结构，通过对每根筋条的应变能进行排序，去除对结构承载没有贡献的筋条，并对剩下的筋条进行局部位置优化，最终获得高承载的新型曲线加筋结构。

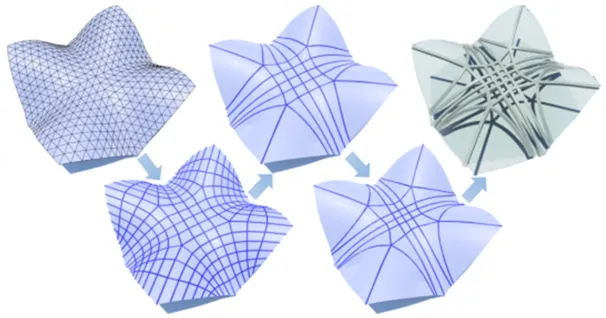
图4 基于主应力线的加筋布局方法[16] Fig.4 Stiffened Layout Method based on Principal Stress Lines

2 变刚度曲线加筋结构的等几何分析

曲线加筋薄壁结构的设计过程对分析方法的效率、鲁棒性和网格自动化提出了挑战。目前，基于板壳理论的商用有限元软件（ANSYS、ABAQUS等）已经能够解决大部分的加筋结构分析。然而，具有复杂几何特征的蒙皮-筋条结构给有限元软件的分析带来了两个难点：a）每次设计迭代之后，整体的网格都需要重新划分，对自动网格划分技术提出了很高的要求；b）几何近似精度是标准有限元分析在处理复杂几何时面临的瓶颈问题，复杂几何意味着精细网格，即规模更大的计算模型，如图5所示。模型复杂度和分析复杂度的增加不利于结构优化[26]。因此，曲线加筋结构分析需要更先进的数值方法。2005年美国Hughes[27]首次提出了基于NURBS基函数的等几何分析方法，并证明等几何分析方法可以有效解决标准有限元网格构建中的高成本、耗时和几何误差等问题。此外，等几何分析方法实现了CAD与CAE的无缝连接，使结构设计过程的自动化更加方便，并被国际公认为“一种替代标准多项式有限元分析的数值方法”。

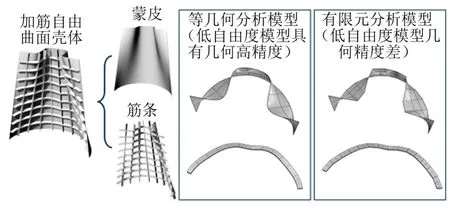
图5 有限元模型与等几何模型的对比 Fig.5 Comparison of the FEA Model and the IGA Model

2.1 基于壳模型的加筋结构等几何分析

筋条是加筋板壳的一个子结构，可通过壳单元建模[28]。由于NURBS张量积造成了四边拓扑限制，单个NURBS片无法表示复杂模型。对于曲筋板壳，必须考虑多片样条几何的等几何分析。多片样条几何的等几何耦合算法包括：罚函数法、拉格朗日乘子法和Nitsche法。耦合方法的鲁棒性对于加筋板壳的设计尤为重要。

2.2 基于梁壳耦合模型的加筋结构等几何分析

对于网格加筋结构，使用壳模型对筋条进行建模的成本极高。使用梁单元可以有效地减少分析变量，且这一优势会随着筋条数量的增加而扩大。因此，基于梁模型的加筋板壳分析方法得到了广泛的研究。为了实现与退化壳单元的耦合，郝鹏等[22]提出了一种NURBS样条加筋单元，该单元基于三维空间退化梁单元，利用NURBS可以精确获取筋条的局部坐标系，筋条单元与蒙皮单元之间的关系如图6a所示。

通过大量的算例验证了该单元对于各类加筋结构的分析具有较高的鲁棒性，特别地，对于复杂曲面蒙皮和变曲率筋条模型，该方法在分析效率和求解精度方法均高于基于有限元方法的商业软件，如图6b所示的一个曲线加筋平板，受到如图6c所示的载荷工况，通过不同分析方法的对比，如图6d和6e所示的等几何分析和ABAQUS分析结果对比，可以明显观察到，等几何分析方法在稀疏网格下就收敛到了商业软件密集网格下的结果。此外，通过改进NURBS投影算法，使其更加适用于曲线加筋结构，大幅提升了曲线加筋结构几何建模的效率和鲁棒性。

图6 基于梁-壳耦合的加筋模型[22] Fig.6 Stiffened Model based on Beam-shell Coupling

3 变刚度曲线加筋结构的优化设计

相较传统常刚度结构，具有更大设计空间的曲线加筋结构增加了优化设计的难度，本节将分别对梯度类、演化类和智能优化方法进行介绍，不同优化方法的对比如表2所示[11]。

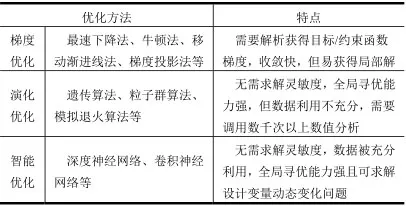
表2 不同优化方法的对比 Tab.2 Comparison of Different Optimization Methods

3.1 梯度类优化

在开展结构的梯度类优化过程中，由于具有明确的寻优方向，往往经过较少次数的数值分析就能获得优化解，因此被广泛地应用到工程结构设计中。

然而，梯度类优化在寻优过程中容易陷入局部最优解。针对NURBS函数表征的曲线加筋结构，Slemp等[3]开展结构轻量化设计，以最小化蒙皮和筋条质量为优化目标。将不同参数的导数进行比较：

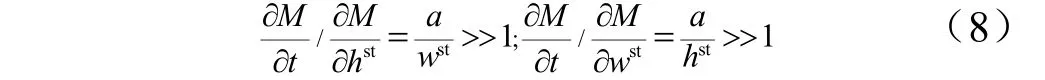
式中a，t分别为平板长度和厚度；hst，wst分别为筋条高度和厚度。其中，设计参数对总质量的不同影响导致梯度优化过程出现收敛速度慢、解不稳定的病态问题。通过对设计变量缩放、移动处理，可以克服此类问题。

针对流函数表征的曲筋布局，王丹等[6]通过均匀化方法获得无加筋平板模型，减少了复杂曲筋结构的建模和分析耗时。以屈曲值λ的倒数为优化目标，等效材料刚度Ce作为中间变量，利用链式法则，获得响应的梯度信息。结果表明，相较的直线加筋构型，流线型曲筋使结构抗屈曲性能提升了50.9%，如图7所示[6]。

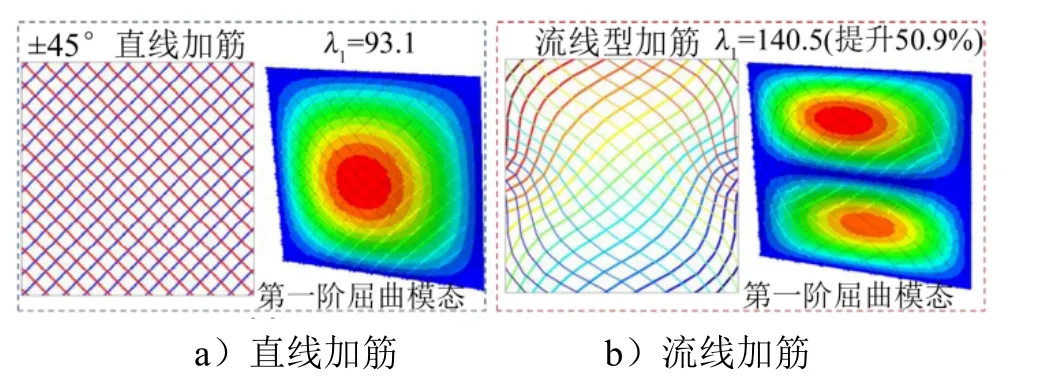
图7 直线和流线加筋布局的对比 Fig.7 Comparison of Straight and Streamlined Stiffened Layout

在曲线加筋的隐式表征中，以数目众多的离散单元作为变量，增加了梯度类优化的求解难度，并且获得的筋条路径连续性差。马祥涛等[14]基于渐进均匀化方法获得无加筋的平板，以最小化应变能作为优化目标，并利用移动渐近线方法开展拓扑优化，经过重构获得清晰的曲筋路径。结果表明，相较于直线加筋构型，曲筋设计使得结构整体刚度提升17%。

3.2 演化类优化

由于演化类优化算法同时对设计空间中的多个解进行评估，减少陷入局部最优解的风险，并且适应度函数不受连续可微的约束，其定义域可以任意设定，这些特点扩大了演化类优化算法的应用范围。

基于PCHIP插值函数，刘大川[11]等利用多岛遗传算法建立了曲线网格加筋结构的一体化设计框架。如表3所示，相较于直筋-均匀分布的设计，曲筋-非均匀分布的优化效率更高，进一步考虑筋条高度和厚度的截面特征，开展曲筋-非均匀-变截面的优化设计，使结构的承载性能进一步提高。

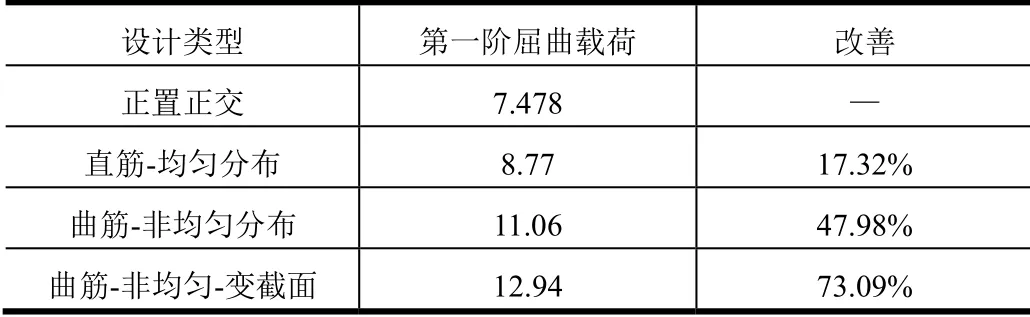
表3 几种加筋类型的优化结果对比 Tab.3 Comparison of Optimized Results for Several Stiffened Types

3.3 智能优化

近年来，人工智能技术迅速发展，在大量数据的驱动下，形成了逼近局部或全局的智能优化机制，为解决复杂结构设计提供了一种极具潜力的优化策略。

Mulani和Joshi等[2,4]建立的响应面代理模型对于结构质量的预测误差小于±1%，代替高保真的数值求解，加快了变刚度曲筋的设计过程。另外，搭建了曲筋设计的专用软件平台：EBF3PanelOpt[4]，可在多种工况下，实现薄板或薄壳的直线、曲线及叶片型加筋设计。

为了加速曲筋的优化过程，Singh等[24]建立了DNNs学习模型，对结构屈曲响应的预测精度达到95%，将优化效率提高了近200倍，但是训练过程需要5万个数据。为了减少数据，Singh等[25]建立了自适应机器学习模型，节约了70%的有限元数值分析计算。

对于贝塞尔函数表征的曲线加筋路径，如图8所示，郝鹏等[10]基于深度学习方法提出了曲筋布局的智能优化框架。由于设计过程中包含众多的连续-离散类型变量，传统代理模型（RBF、Kriging）对于结构响应预测误差%RMSE约为15%，而深度学习模型有效识别曲筋图像特征，预测误差降至5%，大幅度改善模型预测精度。基于该优化框架形成结构变刚度设计软件，为新型曲线加筋结构研究提供一种高效优化工具。

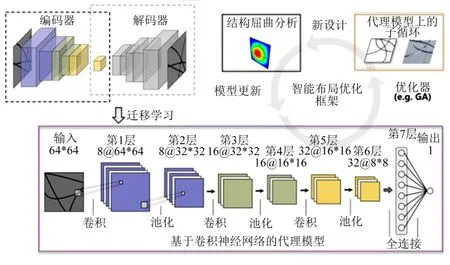
图8 基于深度学习的智能布局设计 Fig.8 Intelligent Layout Design based on Deep Learning

4 结论与展望

基于变刚度曲线加筋结构的全流程设计，本文分别从表征、等几何分析与智能优化3个角度进行了归纳总结。面临的关键技术挑战主要为：a）复杂、不规则的变刚度结构特征的精确调控、建模及分析困难；b）结构细节的激增，为传统优化技术带来了巨大挑战。

为了应对以上技术挑战，进一步的研究方向包括：a）建立基于层次样条的设计-分析-优化一体化模型，突破几何数据结构无法统一、复杂边界收敛性振荡等瓶颈问题；b）建立物理机制引导的领域神经网络和优化框架，实现该类结构的高效、高稳健性设计。