支持控制参数在线优化的气动参数实时辨识方法

钟鸿豪，曹玉腾，郑总准，白文艳，钟 声

（北京航天自动控制研究所，北京100854）

0 引 言

?

目前，飞行器动力学模型的参数大多采用离线辨识方法获得，为设计过程中的控制器设计、系统动态分析及仿真等提供依据。这样的飞行器动力学模型并不完全准确，存在一定的误差，因为在实际飞行过程中，随着飞行条件的改变、飞行器质量的变化、飞行器发生故障或战损导致飞行能力的改变，某些模型参数会产生较大变化。因此，有必要采取在线辨识的方法，实时地获取飞行器模型的各个参数，为飞行控制参数的在线更新、飞行能力在线评估以及飞行器故障检测等提供更加准确的模型[1]。系统辨识的方法主要有方程误差法、输出误差法、滤波误差法等，其中常用的在线辨识算法有递推最小二乘方法（RLS算法）、递推极大似然法、卡尔曼滤波方法等[2]。递推极大似然法对线性和非线性模型都可进行辨识，而递推最小二乘法适用于线性模型。飞行器模型具有高度的耦合性，导致模型阶次较高、未知参数较多，因此飞行器气动参数的辨识比较复杂。

本文提出了一种支持控制参数在线优化的气动参数实时辨识方法。本文对飞行器动力学模型进行了简化，略去耦合因素，选取纵向小扰动线性化模型和纵向非线性模型；在经典的递推最小二乘法的基础上，利用噪声方差的在线估计值对协方差矩阵在线修改，保证递推最小二乘法的收敛速度和辨识精度，实现在线高精度辨识。通过仿真验证了该算法应用于飞行器气动参数辨识的有效性，并对其算法要求、优缺点进行了分析总结。

1 飞行器参数在线辨识模型

1.1 纵向小扰动线性运动模型

考虑一般飞行器的纵向模型的数学表达式[3]如下：

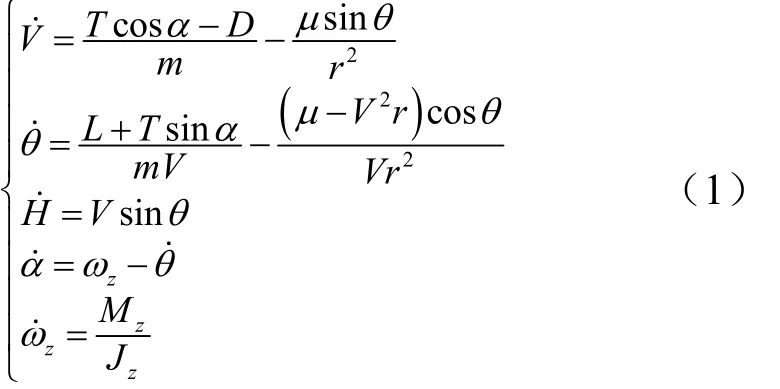
式中V为速度；T为推力；D为阻力；L为升力；m为飞行器质量；μ为地球引力系数；θ为弹道倾角；r为飞行器质心与地心的距离；α为攻角；H为飞行器离地面的高度；ωz为飞行器绕机体Z轴的旋转角速度；Mz为绕机体Z轴的总力矩；Jz为绕机体Z轴的转动惯量。

基于建立纵向运动方程的假设，忽略二阶及三阶小量，同时采用基本假设[4]，将纵向扰动运动方程组在马赫数为15，高度为46 000 m，θ=0°，ωz=0（°）/s的平衡飞行状态下进行小扰动线性化。

利用偏导数的简略表示法，并考虑实际攻角α的数值均比较小，cosα≈ 1,sinα≈α,可得纵向小扰动运动方程组如下：

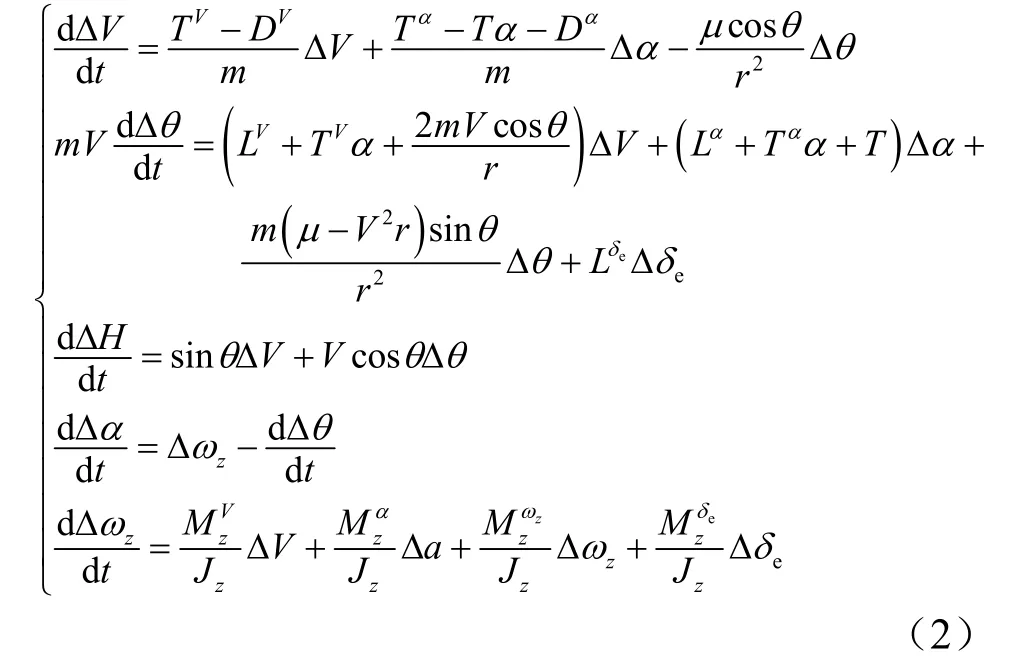
式中 参数的右上角标，表示对该参数的偏导数，如TV表示推力对速度的偏导数。

仅考虑飞行器平飞且速度不变（弹道倾角θ=0，ΔV=0）的飞行过程，整理可得飞行器纵向小扰动线性化模型为

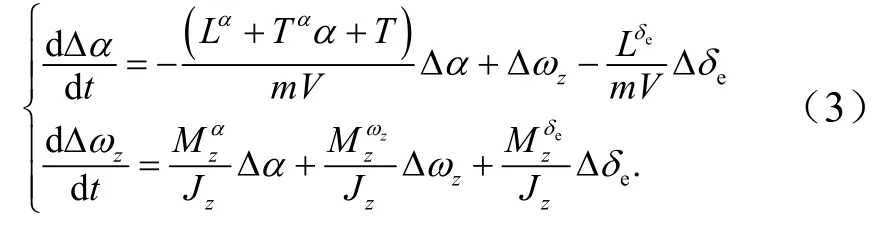
为了便于实现控制参数的在线优化，考虑攻角作为输出量，并将式（3）改写为状态空间表达式的形式：

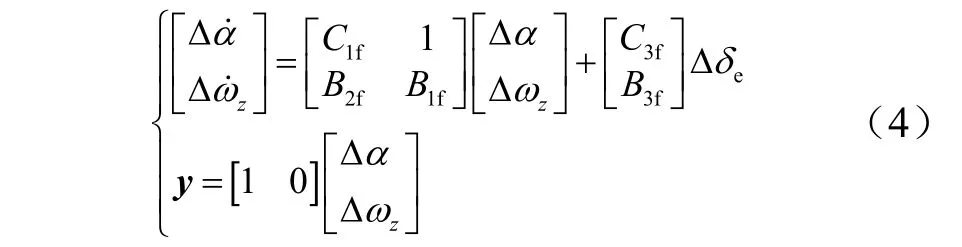
因此，可以得到飞行器纵向模型的小偏差线性化传递函数为

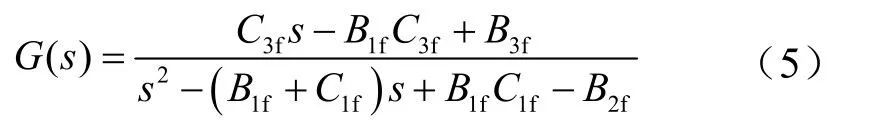
1.2 系统闭环模型

令舵机伺服特性为S(s)，惯组特性为I(s)，控制律为C(s)，舵偏控制指令为δφc，舵偏附加的激励信号为δφs，系统框图见图1，其中，

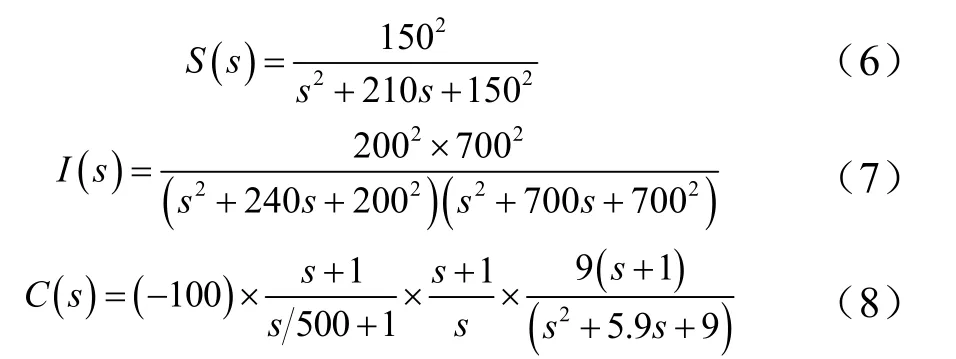
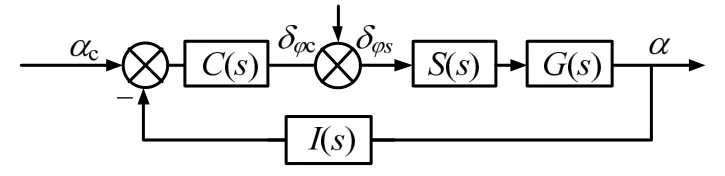
图1 飞行器控制系统框图 Fig.1 Aircraft Control System Block Diagram

1.3 气动参数辨识模型

考虑控制参数对B2f和B3f的依赖较大，选取待辨识参数为B2f和B3f，选取待辨识子系统为

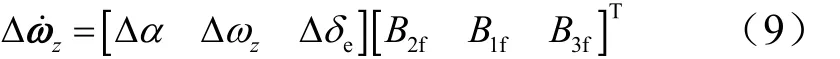
测量方程：

式中Vt为测量噪声。

2 支持控制参数在线优化的气动参数实时辨识算法设计

2.1 带遗忘因子的最小二乘算法

为了实现气动参数的在线辨识，可采用改进的带遗忘因子的最小二乘算法。其中一般的带遗忘因子的最小二乘算法公式如下[2]：

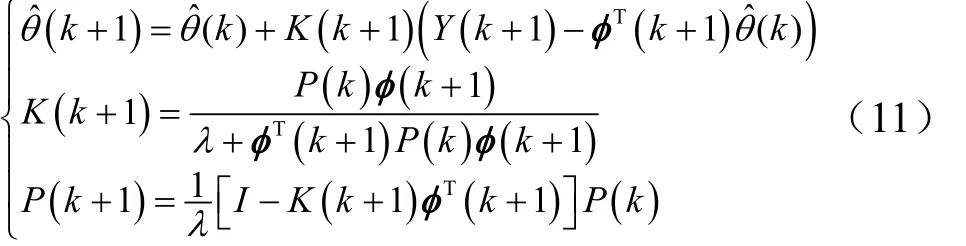
对于第3节得到的飞行器气动参数辨识模型，在k+1时刻，Y(k+1)即为k+1时刻通过惯性测量器件计算得到的角加速度，满足Y(k+1) =Δωz'(k+1) +Vt(k+1)，φ(k+1)为攻角、角速度和俯仰舵偏测量信息，满足：

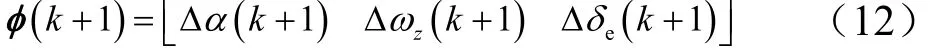
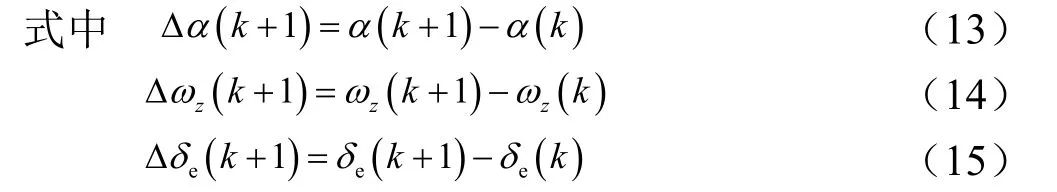
待辨识参数为

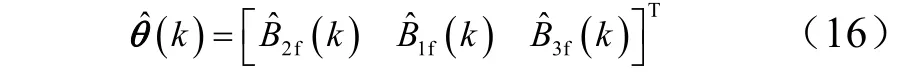
2.2 可变遗忘因子的指数遗忘

为了使遗忘因子λ与当前的状况相匹配，通过监测后验误差控制它的大小。如果e(k)很小，则估计模型与过程匹配得很好，或过程没有被激励。在这两种情况下，应该选择λ(k)≈1。另一方面，如果误差很大，则应该减小λ(k)，以适应模型系数的快速变化，以便跟踪过程特性。

令后验误差加权和为

为使得后验误差的加权和保持恒定，即：

λ(k)选择为

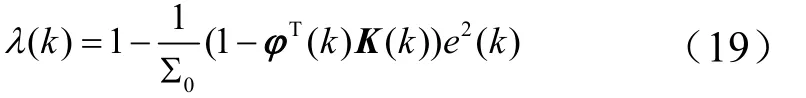
取 Σ0=σ2N0，其中，σ2为噪声方差，可以通过后面的方法估计得到，N0为误差控制因子，且初值满足：

较小的N0值会导致敏感的估计（λ0小），因此可以快速适应参数变化，反之亦然。

2.3 方差的估计

方差2σ的估计，通过下面的递推式子来实现

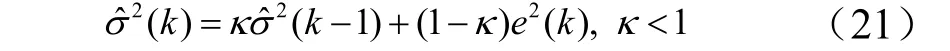
式中κ为方差迭代因子。

得到方差估计值后，可以通过判断相邻时刻方差估计值的变化量来判断待辨识参数的变化情况。

通过设置方差估计值的变化量的阈值来改变，遗忘因子λ的变化范围，从而调整辨识参数和保持辨识结果两种辨识状态，保证辨识结果的准确性。

2.4 协方差矩阵的调整

基于调整遗忘因子λ的估计方法只对缓慢的参数变化过程非常适用，因为校正向量K(k)依赖于只是缓慢变化的协方差阵P(k)。而对于参数快速变化的情况，K(k)和P(k)也必须快速变化，这可以通过为P(k)增加一个矩阵R(k)来实现。

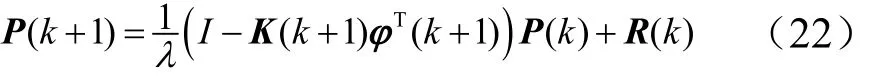
增大协方差阵的元素比仅改变遗忘因子会使参数变化更快，考虑引入如下关系：

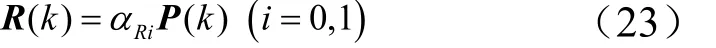
R(k)的值与P(k)的当前变化值关联。αR1＞1的每种情况可以视为一种重启，αR1可取为10或100等大于1的数。

此处需要设置一个判断，防止由于参数变化过快导致()kP不断变大，从而导致辨识结果发散。

采用的方式为，判断新计算出来的(1)k+P行列式的模和(1)k-P行列式的模的比值大小，如果大于所设定 的αR1，则 令 此 时 的αR1=0。即 如 果， 则αR1= 0，

3 仿真验证

针对1.3小节推导的气动参数辨识模型，采用第二节所设计的改进递推最小二乘法，对气动参数进行在线辨识算法仿真。仿真中采样时间为0.005 s， 0.7κ=，参数估计初值取为。根据系统频带特点，不失一般的，激励信号取为

激励之前系统处于稳态，在10～20 s时，施加幅值为1°的激励信号

50 s前气动参数的真值为：C1f=-0 .0017，C3f= 1.6915 ×10-5，B2f=-0 .0317，B1f=-0 .0275，B3f= 0.0225。

50 s时，执行机构突然出现故障，控制能力下降70%，即此时B3f= 0.00675，其他条件不变（试验中，传统最小二乘法，遗忘因子选取为0.95，由于实际飞行中B1f参数值较为准确，辨识中将其当作已知量，仅对B2f、B3f进行辨识）。在无噪声及噪声条件下，分别得到传统恒定遗忘因子辨识方法与本文改进最小二乘方法的辨识结果如下。

3.1 无噪声下仿真结果

针对前面所提到的仿真条件，本文所设计的改进递推最小二乘法与恒定遗忘因子的递推最小二乘法辨识结果，对比见图2。

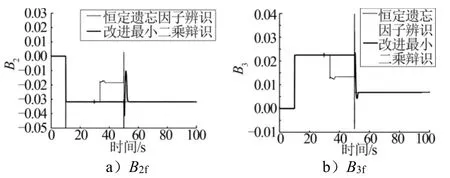
图2 无噪声情况下气动参数的辨识结果 Fig.2 Identification Results of Aerodynamic Parameter without Noise

由无噪声的辨识结果可以看出，当系统处于稳态时（0～10 s），两种辨识方法均无法得到参数的准确辨识结果，在外加激励的时间段（10～20 s），两种方法辨识结果精度均较高，达到95%以上。但是当激励消失时，本文提出的改进最小二乘算法，利用对协方差的估计，可以很好地判断出辨识结果的有效性，不更新精度低的辨识结果，而将上一拍较为准确的辨识结果保留，而恒定遗忘因子的递推最小二乘法，无法对辨识结果进行评估，激励消失后，辨识结果逐渐变差；另一方面，当突发激励（控制能力突然下降）时，改进最小二乘算法仍能较为迅速地辨识得到准确的气动参数值。

3.2 噪声下仿真结果

为了验证方法的抗噪声能力，同样的仿真条件下，在测量的舵偏信号中加入方差为 6.7 ×1 0-9的白噪声，同样可以得到两种方法的辨识结果见图3。

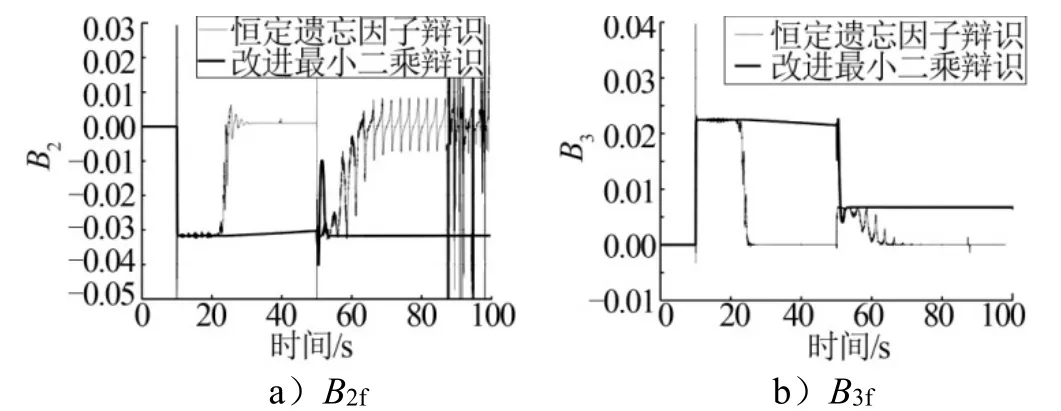
图3 噪声情况下气动参数的辨识结果 Fig.4 Identification Results of Aerodynamic Parameter with Noise

由噪声下的辨识结果可以看出，当系统处于稳态时（0～10 s），两种辨识方法均无法得到参数的准确辨识结果，在外加激励的时间段（10～20 s），两种方法辨识结果精度均较高，达到95%以上。但是当激励消失时，本文提出的改进最小二乘算法，在噪声情况下，仍能利用对协方差的估计，很好地判断出辨识结果的有效性，不更新精度低的辨识结果，而将上一拍较为准确的辨识结果保留，而恒定遗忘因子的递推最小二乘法，无法对辨识结果进行评估，激励消失后，辨识结果迅速变差，辨识结果失效；另一方面，当突发激励（控制能力突然下降）时，同样由于缺乏对于激励信号的捕捉功能，传统恒定遗忘因子的递推最小二乘法，辨识结果较差，而改进最小二乘算法仍能较为迅速地辨识得到准确的气动参数值，并在激励消失时，将其保持，辨识精度达到95%以上，可以满足需求。

4 结 论

本文设计了一种支持控制参数在线优化的气动参数实时辨识方法，根据噪声方差的估计值，在存在激励时快速辨识并收敛，在不存在激励时，将辨识结果保留，保证了辨识结果的有效性。通过仿真试验，本文验证了辨识方法的快速性和准确性，在存在较大噪声的情况下，仍具有较好的辨识性能，该方法辨识结果可直接用于控制参数的在线优化，若应用于工程实践，能减小控制器设计的保守性，提升控制性能，有较强的工程应用价值。