基于粒子群优化算法的高空风弹道修正技术

程光辉，荆武兴，许元男，叶家铭

（1. 哈尔滨工业大学航天学院，哈尔滨，150000；2. 中国运载火箭技术研究院，北京，100076）

0 引 言

导弹在稠密大气层中，由于风干扰影响会产生附加气流攻角。大动压区的风干扰会导致弹体法向的气动载荷增大，引发姿态不稳定[1]。在设计标准轨迹时，为了改善飞行条件，需要考虑由风引起的气流攻角对气动载荷的影响。

余梦伦针对CZ-2E火箭，提出了火箭高空风弹道修正的方法，介绍了高空风修正的原理和方法以及相关的计算模型，达到了改善火箭飞行环境的目的[2]。宋征宇使用基于弹道修正的被动控制技术，以动压q和总攻角η的乘积q η×表示法向风载，通过火箭型号飞行的实际数据，表明了风修正技术能够明显提高飞行的可靠性[3]。Guanghui Cheng改进了高空风弹道修正技术，针对可重复使用火箭大气层内返回段，将统计风场的风速均值和风向均值引入到标准轨迹设计中，并将法向风载q η×当作一个优化指标，基于粒子群优化算法设计标准轨迹，提高了可重复使用火箭的飞行可靠性[4]。在太阳帆的轨迹规划研究领域，传统的根据太阳风平均特性进行电动太阳帆轨迹修正的方法与高空风弹道修正技术原理相同，Caruso基于太阳风动压的实时测量值改进了传统方法，部分抵消了太阳风不确定性对太阳帆的影响[5]。

Eberhart通过模仿鸟群觅食行为，建立了初始的粒子群优化算法[6]。粒子群优化算法由于具有易于收敛和方便操作的特点，已广泛应用于工程实践中[7]，用以解决多变量优化问题。然而，初始的粒子群优化算法易陷入局部极小值陷阱。学者们从3个方面改善粒子群优化算法的搜索能力：a）设计新的拓扑结构；b）引入新的策略或技术；c）与其他算法组合使用[8]。李晶基于动态权重改进的粒子群优化算法设计了惯性稳定平台自适应分数阶参数寻优方法，改善了系统的动态性能和抗干扰能力[9]。将本文的轨迹规划问题转化为一个多变量优化问题，把较弱的风场当作已知信息，利用改进的粒子群优化算法，可以方便地对该优化问题进行求解。

为降低法向风载，改善导弹的飞行条件，本文分析了水平风场模型对弹体运动的影响，给出飞行时序，提出了一种降低法向风载的高空风弹道修正技术，并基于改进的粒子群优化算法，规划了多种工况下的标准轨迹，提高了飞行稳定性。

1 动力学模型与风场模型

1.1 动力学模型

针对导弹的轨迹规划问题，建立质心平动动力学方程：

式中r为质心到参考坐标系原点的位置矢量；v为速度矢量；P为发动机的推力矢量；Q为气动力矢量；m为弹体质量；g为考虑J2项摄动的重力加速度矢量；Isp为发动机比冲。

本文将式（1）中的动力学模型投影到地面发射惯性系下进行仿真分析。地面发射惯性系的原点是发射点O，Ox指向初始瞄准方向，Oy垂直向上，Oxyz构成右手直角坐标系。在导弹发射后，该参考坐标系在惯性空间保持不变。

1.2 水平风的影响

有风时，空气流对弹体有附加速度。地面发射坐标系与发射惯性系的定义相近，不同之处在于地面发射坐标系相对于地面静止不动，因此地面发射坐标系是一个随地球转动的动坐标系。将风速矢量在地面发射坐标系下表示为

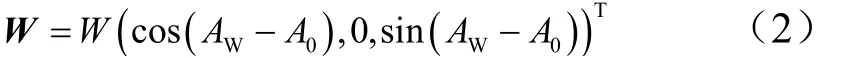
式中W为按高度插值的风速大小；AW为与射向角定义方式相同的风向；A0为发射点处的射向角。

迎风速度矢量为

式中V为导弹在发射系下的速度矢量。

弹体坐标系的原点为弹体质心Ob，Obxb沿弹体外壳的对称轴指向弹头，Obyb在弹体的主对称平面内且垂直于Obxb，Obxbybzb构成右手直角坐标系。地面发射坐标系到弹体系的转换矩阵如下：

式中γ为滚转角，在设计标准轨迹时，设 0γ=；ψ为偏航角；φ为俯仰角。

M1,M2,M3分别为绕x,y,z轴转动的基变换矩阵。

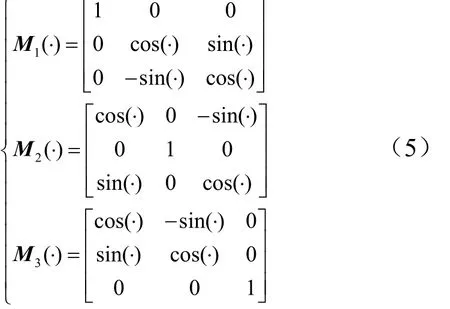
将式（3）中的迎风速度矢量从发射系投影到弹体系上，可得：

速度坐标系的原点为弹体质心Ob，Obxv指向导弹的速度方向，Obyv在弹体主对称面内且垂直于Obxv，Obxv y v zv构成右手直角坐标系。考虑风的影响后，速度坐标系到弹体坐标系的转换矩阵如下：

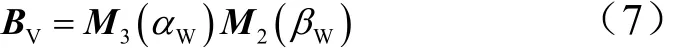
式中αW为风影响下的攻角；βW为风影响下的侧滑角。 将速度矢量由速度系投影到弹体系上，可得：

联立式（6）和式（8），可得风影响下的侧滑角和攻角为

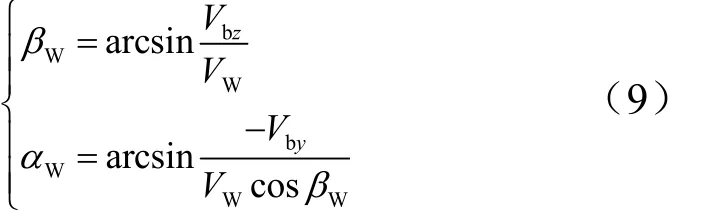
总攻角定义为

法向风载定义为

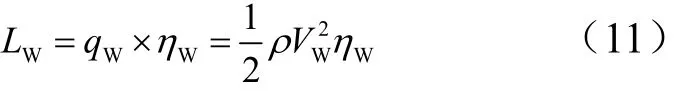
式中ρ为大气密度，其值随高度变化。

1.3 风场模型

1.3.1 基于统计数据的风场模型

相对打击目标处，发射场附近的高空风数据获取难度较低，根据过往的风场观测数据，可以给出某地在某季节按高度节点符合正态分布的风场数据。在射前进行蒙特卡洛打靶仿真飞行实验时，一般采用如表1所示的符合正态分布的风场数据。

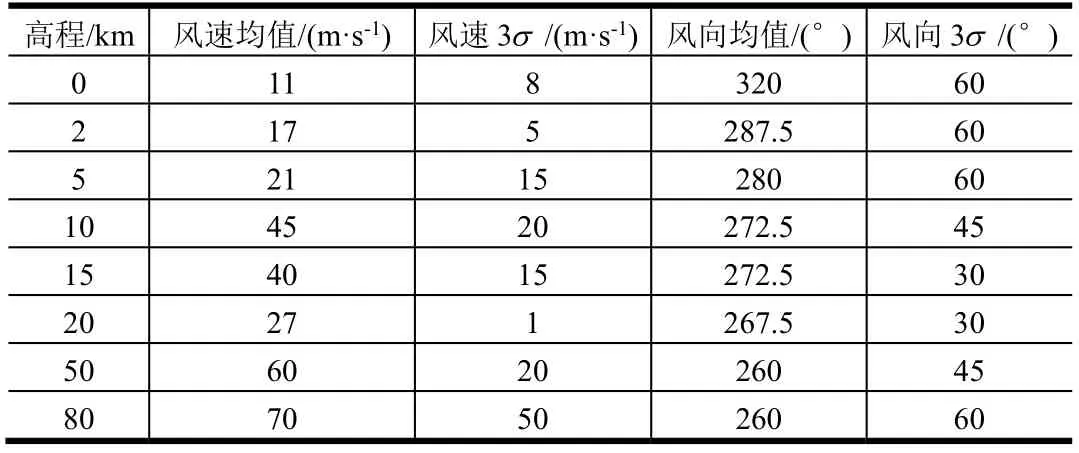
表1 符合正态分布的风场数据 Tab.1 Data of the Wind Field According with Normal Distribution

1.3.2 考虑风切变的风场模型

在极限拉偏仿真时，一般采用考虑风切变的风场模型。平稳风相对于时间和高度变化缓慢。切变风的速度大小随高度急剧增大，然后急剧减小，一般以三角波的形式，在一定高度范围内加入切变风。风剖面如图1所示。

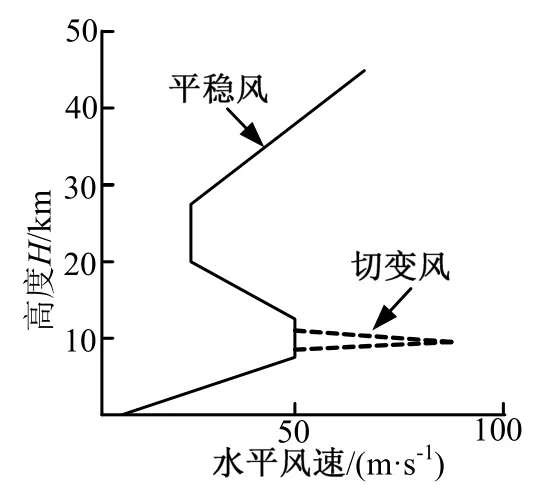
图1 风剖面 Fig.1 Wind Profile Figure

考虑风切变的水平风场数据如表2所示，平稳风风速稍大于表1中的风速均值。

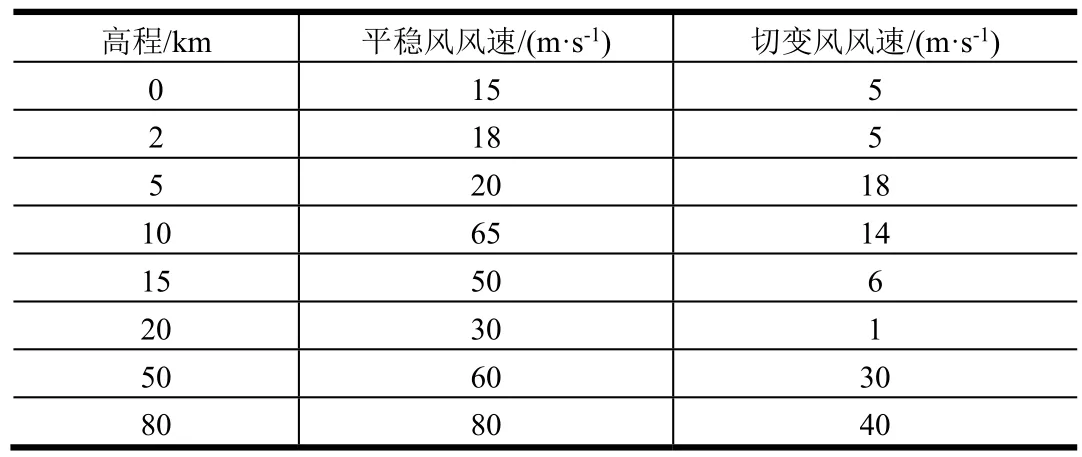
表2 考虑风切变的风场数据 Tab.2 Data of Wind Field with Shear Wind

2 弹道修正技术

在设计标准轨迹时引入预置风场，选择合适的指令攻角变化律，基于粒子群优化算法，将风载最大值通过罚函数法转化为优化指标，可降低法向风载最大值，改善飞行器的抗干扰性能。

2.1 飞行时序

参考文献[10]，制定表3所示的飞行时序。由于本文关注法向风载对飞行轨迹的影响，采用了以指令攻角和侧滑角为主的飞行时序设计思路。

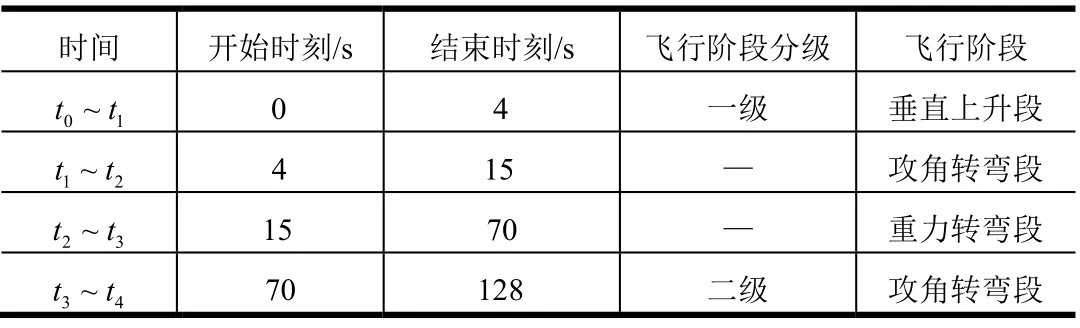
表3 飞行时序 Tab.3 Flight Profile

在一级垂直上升段，指令俯仰角为90°，指令偏航角为0°。

在一级攻角转弯段，无风干扰的情况下，指令攻角的变化规律为

式中t为飞行时间；αm1为一级攻角转弯段指令攻角最大值；tm1为指令攻角达到最大值的时刻。

在一级重力转弯段，无风干扰的情况下，指令攻角与指令侧滑角均为0。在设计标准轨迹时，为避免气动载荷对弹体运动产生较大的影响，本阶段需包括跨音速段和动压最大值点。

在二级攻角转弯段，无风干扰的情况下，指令攻角变化律如式（13）所示。

式中αm2为二级攻角转弯段指令攻角最大值；tm31为指令攻角达到最大值的时刻；tm32为指令攻角由最大值开始减小的时刻，即在tm31～tm32时段内，指令攻角保持最大值αm2。

2.2 高空风弹道修正技术

传统的高空风弹道修正技术要求在跨音速段和最大动压段的气流攻角为零，即弹体纵轴与迎风速度矢量共线。为避免指令攻角因为引入风场而发生突变，将风速与一个随时间变化的“梯形系数”相乘，使得风速由0开始增加至预置风速，经过一段时间，再缓慢减小至0。设在规划标准轨迹时引入的风速大小为Wsm，各飞行阶段实际使用的预置风场的风速大小为Ws，则有：

随时间变化的“梯形系数”KW（t）见表4。一级重力转弯段包含跨音速点和最大动压点，是风干扰影响最大的阶段，系数KW（t）设为1。

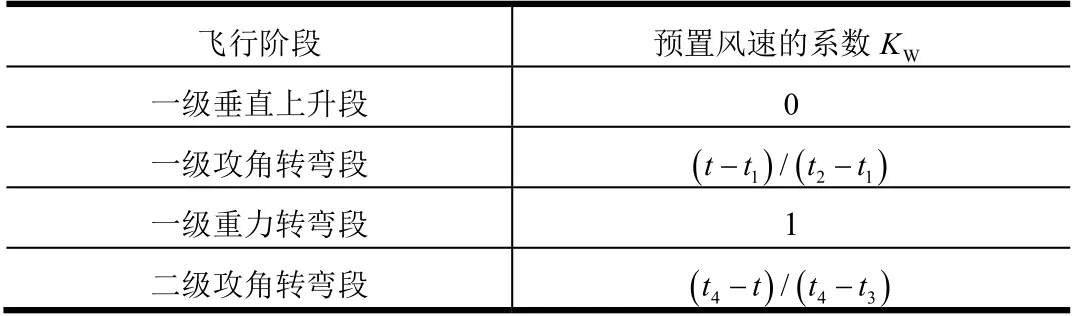
表4 预置风速的梯形系数 Tab.4 Trapezoidal Coefficients for the Preset Wind Speed

一般基于工程经验或气象统计资料给定预置风场的风速与风向数据。本文中预置风场的风速有2种来源：a）统计风场平均风速，见表1，设 smW为0.25倍的风速平均值；b）平稳风，见表2，设 smW为0.25倍的平稳风风速。预置风场的风向有2种来源：a）不随高度变化的恒定风向，范围为[0,360)° °；b）统计风场中随高度变化的风向平均值。对于不同区域的发射需求，需要根据当地气象统计资料，确定多条用于设计标准轨迹的预置风场数据，在气象部门给出当前风场预测结果后，选取最为接近的预置风场对应的诸元进行装订。

若引入与弹道平面存在夹角的风场，会使得轨迹在偏航方向产生偏差，则需在二级飞行阶段引入非零的指令侧滑角，对飞行轨迹在偏航方向的偏差进行修正。二级飞行阶段指令侧滑角的变化规律与式（13）中指令攻角的变化规律相近，为

基于式（9）和无风干扰时指令攻角和指令侧滑角的变化规律，风影响下的攻角和侧滑角增量为

将式（16）中风攻角和侧滑角增量与不考虑风干扰的指令攻角和指令侧滑角相结合，使得标准轨迹中指令攻角和指令侧滑角按照式（17）进行修正。式（17）为本文提出的“引入风攻角增量进行弹道修正”的方法。

式中Kalf为攻角修正系数。

综上所述，在使用高空风弹道修正技术设计标准轨迹时，需要优化的变量有：

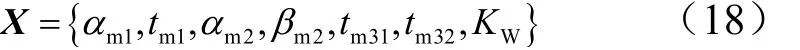
“引入风攻角增量进行弹道修正”的方法比较依赖于当地气象统计资料。若将式（11）定义的法向风载引入到优化指标中，在无风工况下，亦能优化出法向风载较小的飞行轨迹，即是“引入法向风载最大值作为优化指标”的方法。

以飞行终点即头体分离处的状态为约束，将式（11）定义的法向风载引入到优化指标中，基于罚函数法设计如下优化指标：

式中 下角标f，E分别表示实际和期望的终端状态；h为飞行高度，km；θ为速度倾角；σ速度偏角，rad；Kh，Kθ，Kσ，KL分别为对应的罚函数系数，Kh=1，Kθ= 57.30，Kσ= 57.30，KL=1 × 10-3。KL越大，降低法向风载最大值的效果越明显。

式（19）中，除法向风载LW外，其他优化指标可根据实际工程需要进行选取。

基于式（18）和式（19），本文所定义的轨迹优化问题为

优化指标F的值越小，对应的解越优。

3 粒子群优化算法

粒子群优化算法通过粒子群内部信息交换的方式解决优化问题。在式（18）构成的N维解空间中，设有M个粒子。第i个粒子在第t次迭代中的位置和速度矢量为

式中d为区间[1,N]内的正整数。

优化变量的位置和速度边界如下：

式中

第i个粒子的历史最优解记作pi，所有粒子的最优解记作pg。第i个粒子的速度矢量vi和位置矢量xi更新公式如下

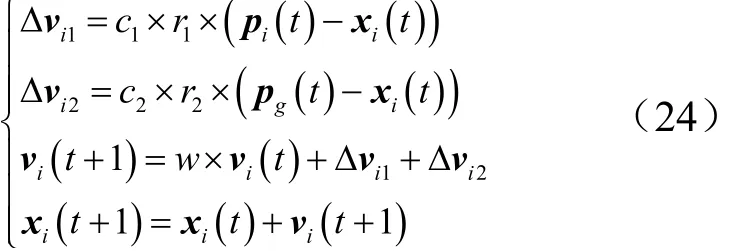
式中r1和r2为[0,1]内的均匀分布随机数。

惯性权重w较小时，粒子群优化算法的局部搜索能力较强，w较大时，粒子群优化算法的全局搜索能力较强。惯性权重随迭代次数线性下降的变化规律[11]如下：

式中 惯性权重最大值wmax= 0.9；惯性权重最小值wmin=0.2；tmax为最大迭代次数。

时变的加速因子c1和c2有利于改善粒子群优化算法的搜索效率，加速因子随迭代次数线性变化的规律[12]如下

式中 时变加速因子的最大值为cmax=2.5，最小值为cmin=0.2。

为赋予粒子群优化算法跳出局部极小值的能力，当某个粒子靠近当前最优粒子且速度极小时，重新初始化该粒子的速度矢量。设置“重新初始化”规则[4]为

式中ε为一个较小的正数，本文取为 1 × 10-5。

式（27）中归一化后的距离Dxi和速度Dvi为

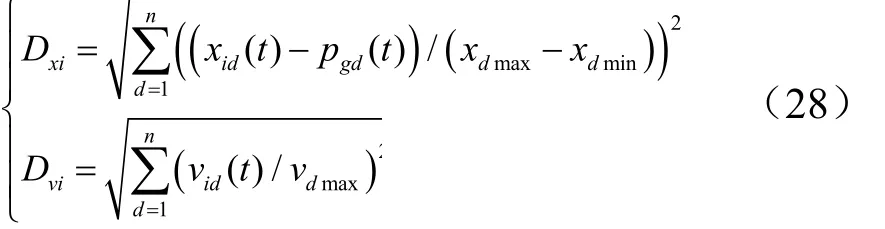
即当D xi≤ε且D vi≤ε时，使用均匀分布随机数重新初始化第i个粒子的速度矢量。

粒子群优化算法的流程如图2所示。

图2 粒子群优化算法流程 Fig.2 The Flow Chart of the Particle Swarm Optimization Algorithm

4 仿真分析

本文瞄准头体分离点终端约束，设计多种工况下的标准轨迹，验证本文提出的高空风弹道修正技术的有效性。

4.1 仿真参数

发射系原点的大地纬度和大地经度均为0°，发射方位角为270°，海平面高度为0。采用冷发射模式，初始高度为50 m，初始速度为15 m/s。制导周期为 0.1 s。

头体分离点约束中，高度为147.3556 km，地面发射惯性系下的速度倾角为43.1525°，速度偏角为0°。

飞行参数见表5。

表5 飞行参数 Tab.5 Flight parameters

式（18）中优化变量的范围见表6。为限制转弯时的法向过载值，基于表3中的飞行时序，选取了合适的时间变量范围。

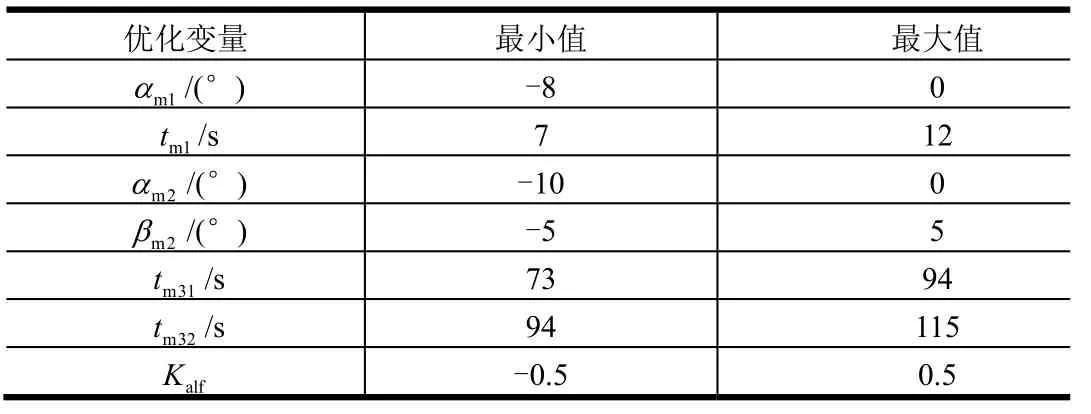
表6 优化变量的范围 Tab.6 Ranges of Optimized Variables

4.2 仿真结果与分析

为验证本文提出的改进弹道修正技术在多种工况下的有效性，本节选取了5种仿真场景：a）工况1，预置风场的风速Wsm为0；b）工况2，预置风场取自表，即风速Wsm为0.25倍的风速均值，风向为风向平均值；c）工况3，预置风场取自表，即风速Wsm为0.25倍的风速均值，风向为风向平均值偏转90 °；d）工况4，预置风场取自表，即风速Wsm为0.25倍的平稳风风速，风向为270 °；e）预置风场取自表，即风速Wsm为0.25倍的平稳风风速，风向为360 deg。

将式（17）中“引入风攻角增量进行弹道修正”作为变量1，将式（19）中“引入法向风载最大值作为优化指标”视作变量2。变量1与变量2共同组成了本文提出的改进高空风弹道修正法。将引入2种变量的操作进行组合，得到如表7所示的标准轨迹分组。

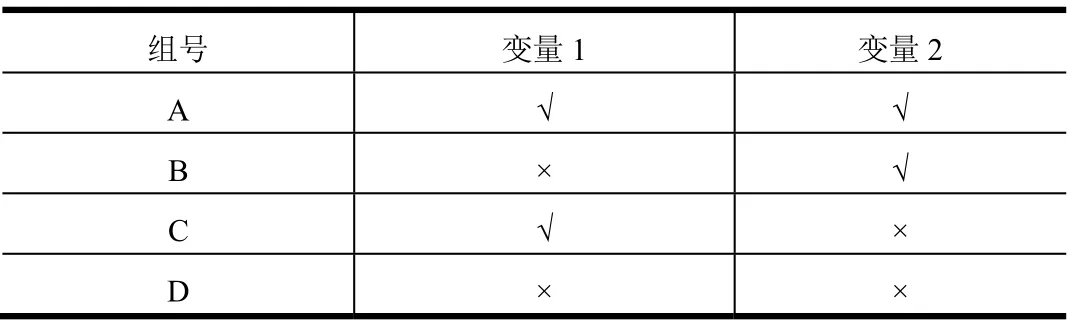
表7 标准轨迹分组 Tab.7 Groups of the Standard Trajectories

工况1（无风工况）的各组法向风载随时间变化曲线见图3。图中法向风载的变化趋势与总攻角的变化趋势相近。

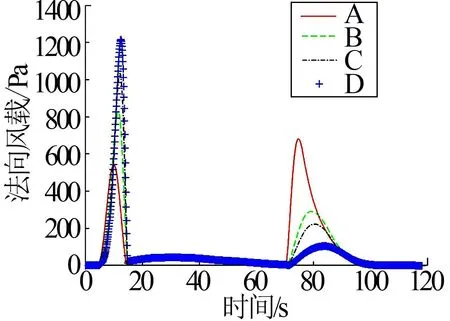
图3 法向风载随时间变化曲线（工况1） Fig.3 Normal Wind Load Curve Concerning Time (Scenario 1)

工况2的各组法向风载随时间变化曲线见图4。由于引入了预置风场，在不使用弹道修正技术的D组，一级重力转弯段法向风载最大值为1482.6 Pa。在使用了改进弹道修正技术的A组，法向风载最大值减小为981.1 Pa。

图4 法向风载随时间变化曲线（工况2） Fig.4 Normal Wind Load Curve Concerning Time (Scenario 2)

工况3的各组法向风载随时间变化曲线见图5。

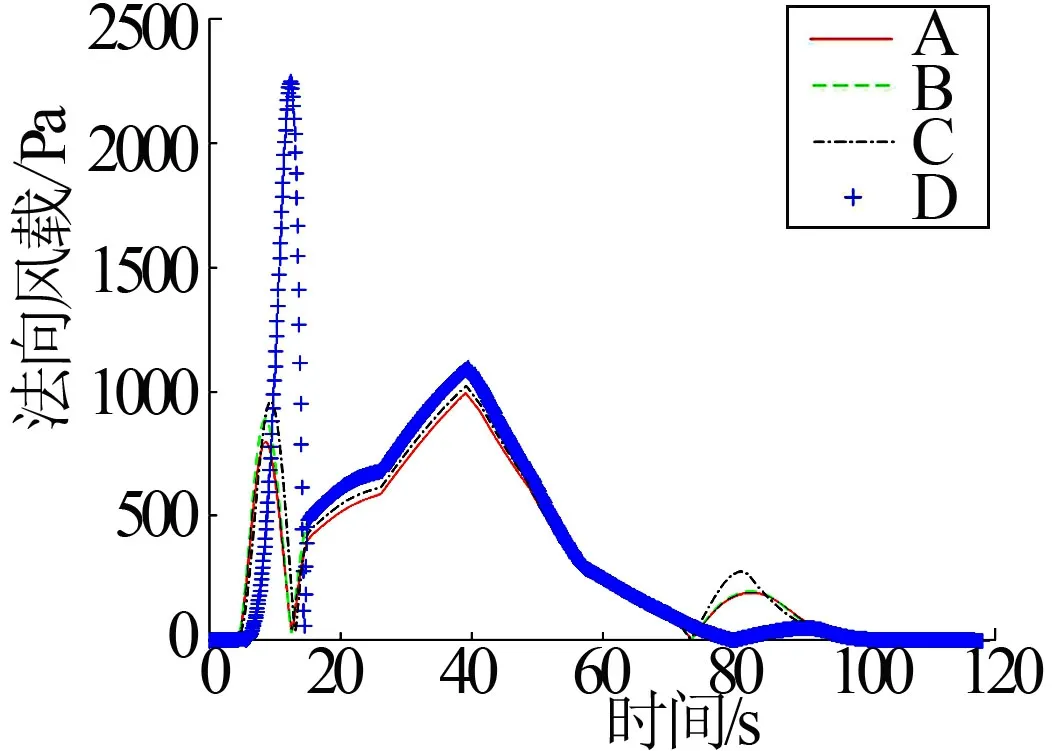
图5 法向风载随时间变化曲线（工况3） Fig.5 Normal Wind Load Curve Concerning Time (Scenario 3)

工况4的各组法向风载随时间变化曲线见图6。考虑风切变的风场模型中，平稳风的风速稍大于统计风场的平稳风速，因此图6中一级重力转弯段的法向风载值大于图4和图5。

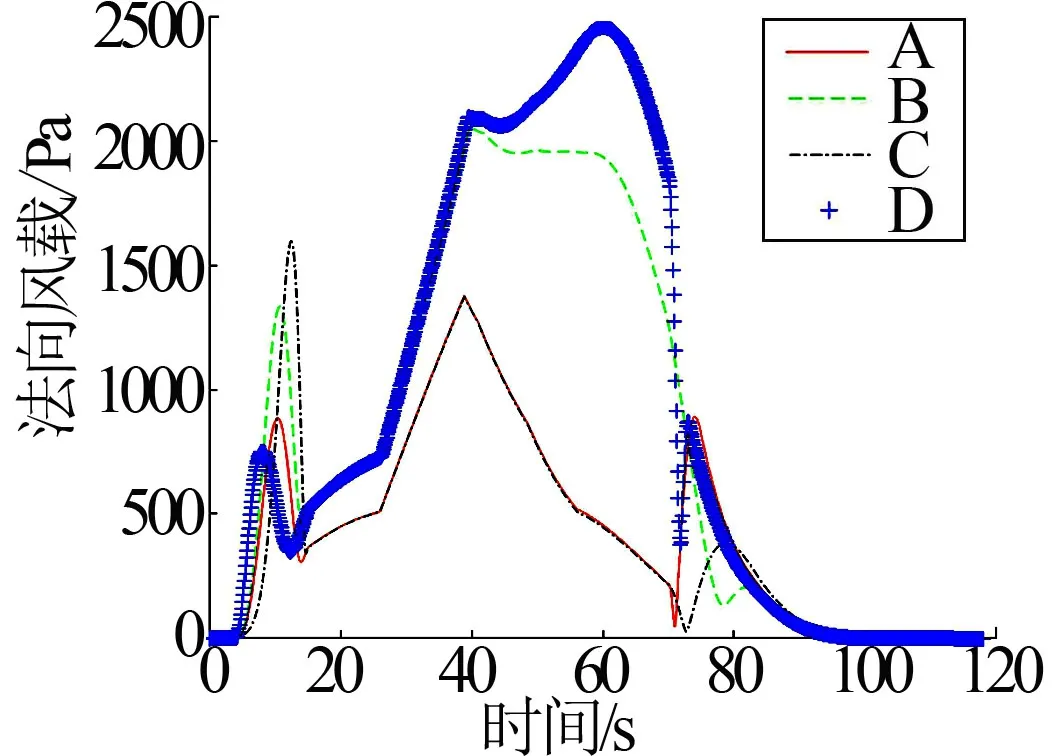
图6 法向风载随时间变化曲线（工况4） Fig.6 Normal Wind Load Curve Concerning Time (Scenario 4)

工况5的各组法向风载随时间变化曲线见图7。

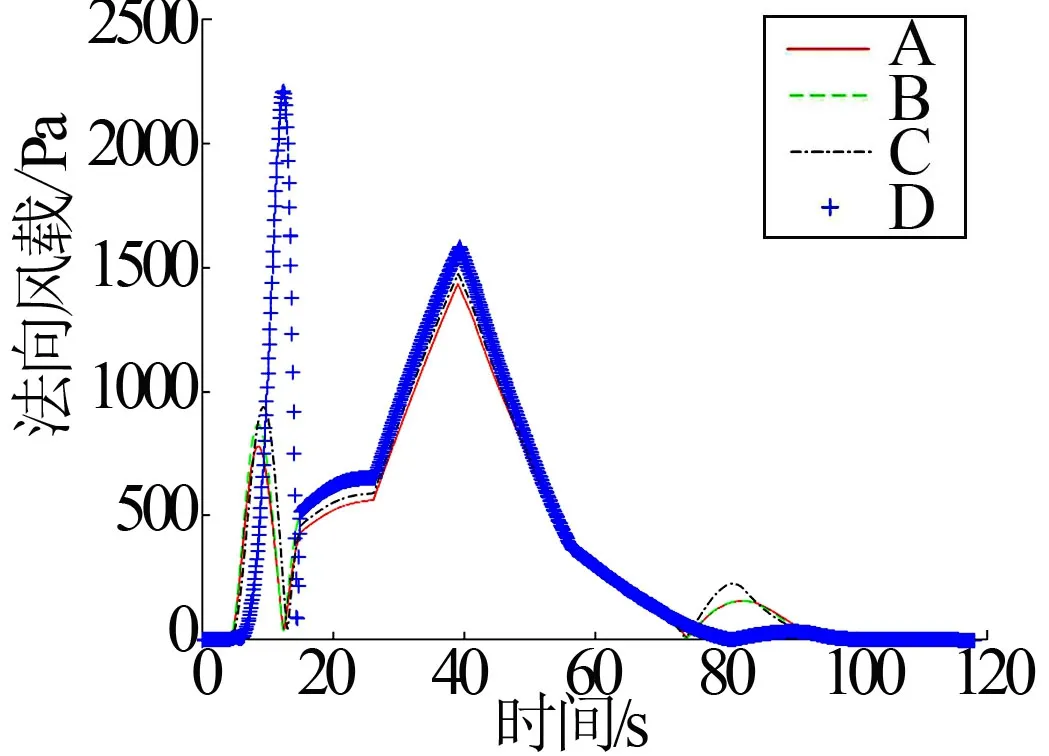
图7 法向风载随时间变化曲线（工况5） Fig.7 Normal Wind Load Curve Concerning Time (Scenario 5)

各工况下的法向风载最大值见表8。采用“引入风攻角增量进行弹道修正”和“引入法向风载最大值作为优化指标”的A组相对于D组，法向风载最大值分别减小了43.91%、33.83%、55.77%、43.98%和35.10%。仅使用“引入法向风载最大值作为优化指标”的B组相对于D组，法向风载最大值分别减小了31.87%、1.83%、50.98%、16.21%和28.07%。

表8 法向风载最大值 Tab.8 Maximum Values of Normal Wind Load

5 结 论

本文为了降低法向风载，提高导弹的飞行稳定性，提出了一种改进的高空风弹道修正法。以动压与总攻角的乘积表示法向风载，在规划标准轨迹时引入预置风场，计算风攻角和风侧滑角增量，并引入攻角修正系数，修正了指令攻角和指令侧滑角，将法向风载最大值当作优化指标，基于改进粒子群优化算法，规划标准轨迹。仿真结果表明，相对于不使用高空风弹道修正法的案例，改进的弹道修正法使得法向风载最大值减小了33.83%～55.77%，能够提高飞行稳定性。