基于正演模拟的高速底砾岩振幅屏蔽特性分析及补偿

明 君,彭 刚,王建立

(中海石油(中国)有限公司天津分公司,天津300459)

在许多油气储量丰富的海上探区,地下地层中存在着不稳定分布的底砾岩。由于底砾岩速度、密度等物理性质远高于周围地层,因此形成了强反射界面,对地震波场产生了极强的屏蔽作用,导致底砾岩下伏地层地震资料品质差。在含底砾岩探区的实际地震资料的处理和解释过程中,发现底砾岩下伏地层成像时出现明显的“能量阴影”,均方根振幅(root mean square,RMS)属性能量分布不均匀,强弱变化较快,这种现象通常被称为强振幅屏蔽,对构造和储层的精细研究以及储量的准确估算造成了极大的挑战。

前人已经开展过大量地震勘探中强振幅屏蔽的研究。吴志强等[1]、王建花等[2]根据地震波能量定量计算的结果,认为界面上、下地层速度比越大,屏蔽作用越强;郭树祥[3]通过建立不同类型的火成岩模型,分析了正演模拟单炮的屏蔽效应;刘立民等[4]将逆时偏移技术应用于振幅屏蔽区域,其成像效果明显优于Kirchhoff叠前深度偏移的结果;王志等[5]对强振幅屏蔽下弱反射界面的广角反射法进行了反射特征及影响因素的研究;张军华等[6]对声波测井以及录井资料进行了正演模拟,分析了受强振幅屏蔽影响地层的地球物理机制;还有一些学者对底砾岩等高速屏蔽层的物性特征、地质形态进行了大量的研究[7-10]。这些研究成果有助于我们认识振幅屏蔽效应的特征。为实现强振幅屏蔽补偿,目前常用的一种思路是从强反射界面的剥离或压制的角度出发,突出强反射界面下伏屏蔽层的能量。江馀等[11]应用优化后的模态分解技术,剥离了强反射界面的能量,从而增强了下伏屏蔽层的能量强度;朱博华等[12]采用匹配追踪法分离了油页岩强反射界面;顾雯等[13]利用地震波形的横向变化信息替代变差函数,完成了高频信息的井震联合反演,削弱了强反射界面的影响;张宪旭[14]采用了基于模型驱动的煤层强反射能量衰减方法压制实际煤层反射,取得了良好的效果。强振幅屏蔽通常是多种影响因素共同作用的结果,从剥离或压制强反射界面的角度提出的许多针对强屏蔽层的振幅补偿技术不具有普适性,难以从根源上解决屏蔽问题。因此从理论分析的角度进一步加强对强振幅屏蔽的研究,并且提出合理补偿方案,对于海上含底砾岩探区的高精度成像和油气储量预测具有重要的意义。

实测地震数据中的强振幅屏蔽受到地下介质等多种因素的综合影响,各种因素的影响程度难以区分和量化。正演模拟可以基于控制单一变量的原则,逐个对影响因素进行模拟分析,分别得到它们对强振幅屏蔽的影响程度,有助于更准确地认识强振幅屏蔽的特征,排除其它地下介质因素的干扰。本文首先针对不同形态特征及物性参数的底砾岩,建立了不同的正演模型,利用弹性波动方程对正演模拟数据进行了逆时偏移处理;其次对正演地震数据的逆时偏移(reverse time migration,RTM)成像剖面进行了沿层振幅统计,计算出了屏蔽比例系数,对不同形态的底砾岩所造成的强振幅屏蔽进行了量化分析,得出了不同因素导致的屏蔽效应的强弱关系;最后根据前人的研究成果以及生产过程中积累的经验,分别从地震数据采集和处理两个方面提出了削弱强振幅屏蔽影响以及能量补偿的方案,并将其应用于正演地震数据和实际地震数据的能量补偿,以验证方法的有效性。

1 弹性波能量分配原理

当弹性纵波传播到介质分界面上时,一部分能量继续透过界面向下传播,称为透射波;另一部分能量反传回界面上覆介质中,称为反射波。地震观测系统可以接收到传播到地面的部分能量,该部分能量反映了该界面在地震剖面中能量的强弱。为了描述上述反射透射关系,佐普里兹在1919年推导出了Zoeppritz方程[15]。

假设在由两种半无限弹性介质形成的分界面上,该界面上覆介质称为介质1,下伏介质称为介质2,传播至该界面的平面简谐纵波产生反射纵波、反射横波、透射纵波、透射横波4种波场。α为入射纵波的入射角和反射纵波的反射角,β为反射横波的反射角,α′为透射纵波的透射角,β′为透射横波的透射角。纵、横波的反射和透射系数均可用如下的Zoeppritz方程表示:

(1)

式中:ρ1和ρ2分别表示介质1和介质2的密度;vP1,vP2分别表示介质1和介质2的纵波传播速度;vS1,vS2分别表示介质1和介质2中的横波传播速度;RPP表示反射纵波的反射系数;RPS表示反射横波的反射系数;TPP表示透射纵波的透射系数;TPS表示透射横波的透射系数。利用上述方程,我们可以根据地震波的入射角以及地层的弹性参数,计算出反射系数的值,进而可以推算出反射波的能量。

Zoeppritz方程非常复杂,难以推导出其解析解。为此,许多学者进行了大量简化Zoeppritz方程解析解的研究[16-18]。其中,应用最为广泛的是SHUEY在1985年提出的Zoeppritz方程近似公式——Shuey公式,该公式的使用前提是界面两侧介质的弹性系数变化小,具体公式如下:

(2)

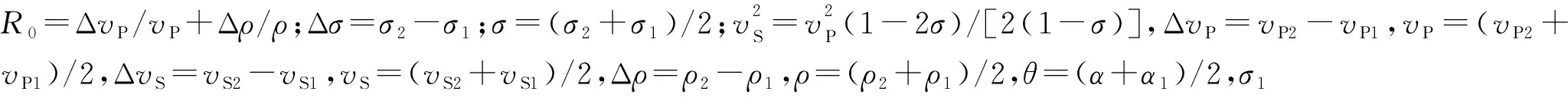
2 强屏蔽层正演模拟及成像分析

通过前文对Shuey公式的分析可知,地下岩性突变的异常介质会对振幅产生显著影响,本文的研究目标底砾岩为地下一种典型的岩性突变介质。围绕底砾岩的物理性质及展布特点进行正演,主要考虑受强振幅屏蔽影响的地层深度、底砾岩的长度、厚度、层数及速度5个因素,并分析其对强振幅屏蔽的影响程度。图1为含底砾岩的基础速度模型,模型长3000m,深1000m,图中仅显示局部,共有6套水平层位及多套底砾岩,其具体参数见表1。后续章节所采用的正演速度模型都是以此模型的物性参数为基本框架,通过修改前述的某一物性参数(如地层深度、底砾岩长度等)衍生而成。修改的参数值会在文中特别说明,其他未作说明的参数值与此基础速度模型一致。对底砾岩下伏的三个反射界面由浅至深分别标记为R1、R2、R3,由于反射界面R2相邻的上下两层介质的波阻抗与反射界面R2的波阻抗差异较小(具体数值见表1),导致R2产生的反射波振幅也远小于R3产生的反射波振幅。为便于对试验结果的分析和描述,后续章节所述正演模型继续沿用此标号。本节所述各种速度模型皆采用同一观测系统进行正演模拟,炮间距为25.0m,道间距为12.5m,每炮80道接收。正演模拟的子波为主频25Hz的雷克子波,算法为弹性波有限差分方法,共80个炮集。对模拟数据没有应用振幅补偿等技术,从而保证处理所得成像剖面的保幅性和后续振幅分析的准确性。

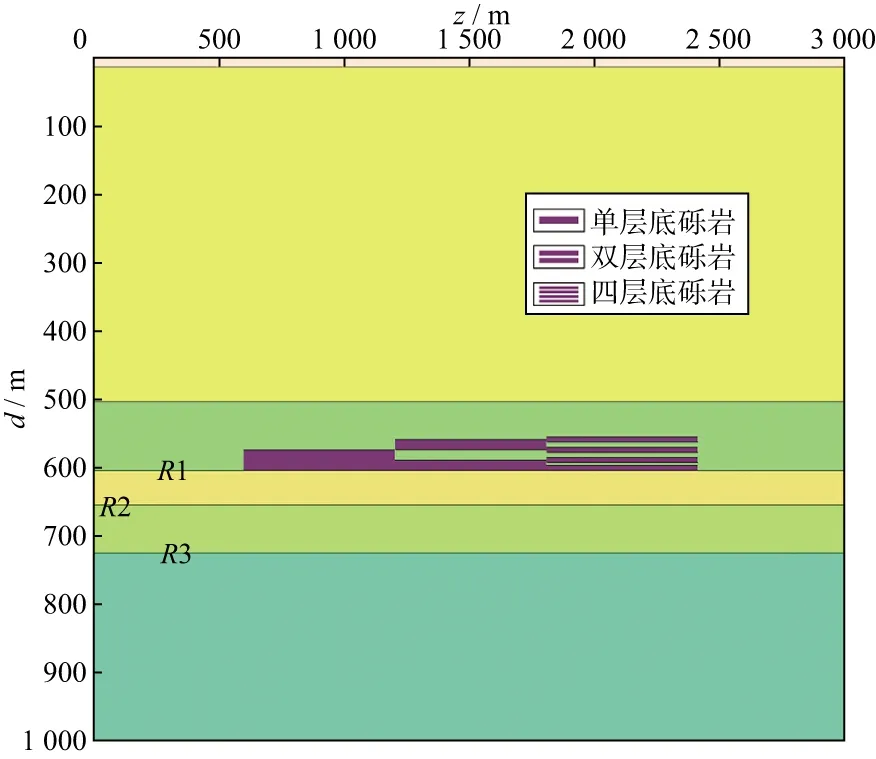
图1 含底砾岩的基础速度模型

表1 正演速度模型层状介质弹性参数

2.1 不同反射界面深度

图2为3种不同深度反射界面的RTM成像剖面(图左)及其速度模型(图右),其中图2a,图2b和图2c对应反射界面R3的深度分别为700,800,900m,用于分析研究不同地层深度受强振幅屏蔽的影响程度。

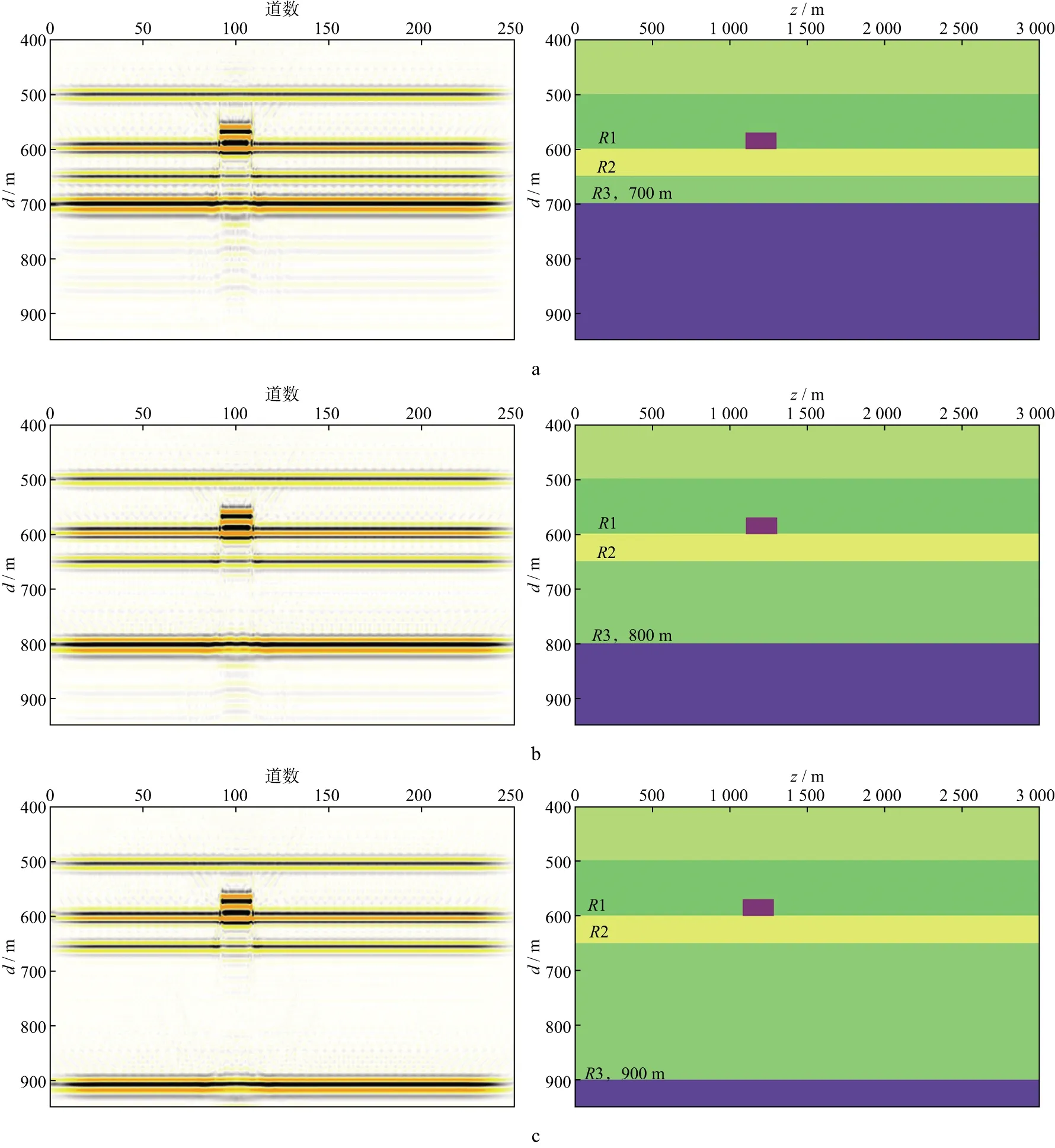
图2 不同深度反射界面的RTM成像剖面(左)及其对应的速度模型(右)a 700m; b 800m; c 900m

图3为不同深度反射界面的RTM成像剖面沿层统计的振幅曲线,分别对应图2中RTM成像剖面同相轴R1,R2,R3的振幅强度。其中图3a至图3c 分别对应的反射界面R3的深度为700,800,900m。由振幅曲线可以看出,由于3种模型的R1,R2相关参数全部相同,其曲线的形态也保持一致,其中反射界面R1的振幅曲线在底砾岩区域表现出振幅增强的特性,而其下方的反射界面R2的振幅曲线在底砾岩区出现明显的振幅减弱,即振幅屏蔽现象;随着3种模型中的反射界面R3深度的增加,振幅屏蔽的强度逐渐减小(图3a至图3c所示的R3界面),但整体对振幅的影响程度较小,通常小于10%。

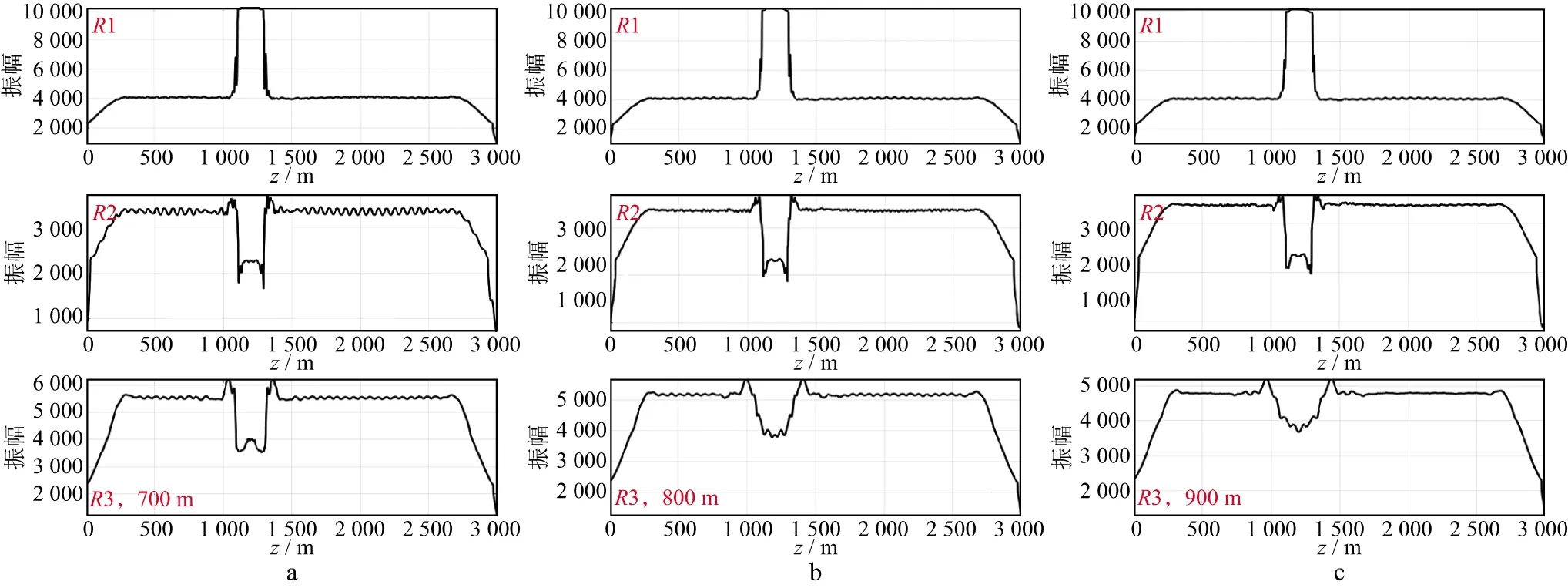
图3 不同深度反射界面的RTM成像剖面沿层统计的振幅曲线a 700m; b 800m; c 900m

2.2 不同底砾岩长度

图4为含有不同长度底砾岩的RTM深度剖面及其相应的速度模型,3块底砾岩的其它参数相同,长度从左到右依次为200,400,600m,通过长度的变化,研究其对振幅屏蔽的影响程度。

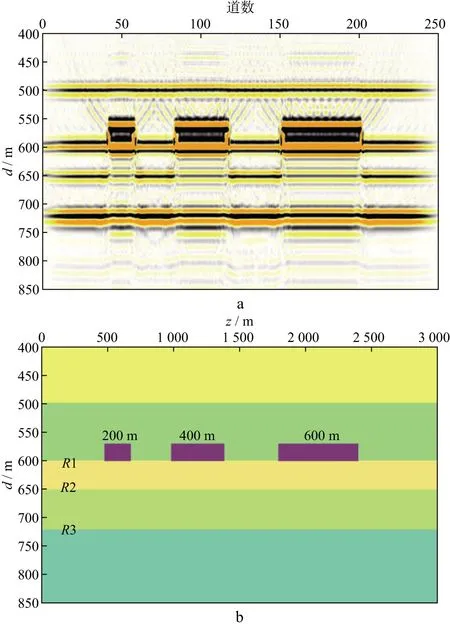
图4 含不同长度底砾岩的RTM深度剖面(a)及其对应的速度模型(b)

图5为对图4a中含不同长度底砾岩的RTM深度剖面沿层统计的振幅曲线,图5a至图5c分别为反射界面R1,R2,R3的沿层统计的振幅曲线。可以看出,反射界面R1的振幅曲线中出现3个振幅增强的区域,即反射界面R1的振幅曲线在底砾岩区域会表现出强振幅的特性,振幅增强的幅度一致,但范围随着底砾岩长度的增加而增加;在底砾岩下方的反射界面R2,R3的振幅曲线中,出现了3个振幅减弱的区域,即存在振幅屏蔽现象,同一层不同长度的底砾岩的屏蔽的幅度相同,但屏蔽的范围随着底砾岩长度的增加而增大。

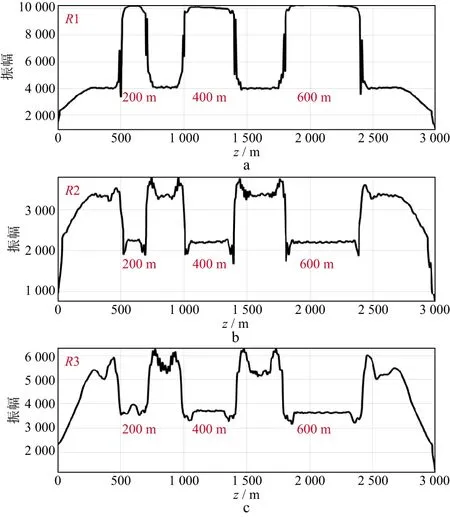
图5 对图4a中含不同长度底砾岩的RTM深度剖面沿层统计的振幅曲线a R1; b R2; c R3

2.3 不同底砾岩厚度

图6为含有不同厚度底砾岩的RTM深度剖面及其对应的速度模型,在3组底砾岩的其它参数相同的条件下,厚度从左到右依次增大,分别为7.5,15.0,30.0m,通过改变底砾岩的厚度,量化分析该参数对振幅屏蔽强度的影响。

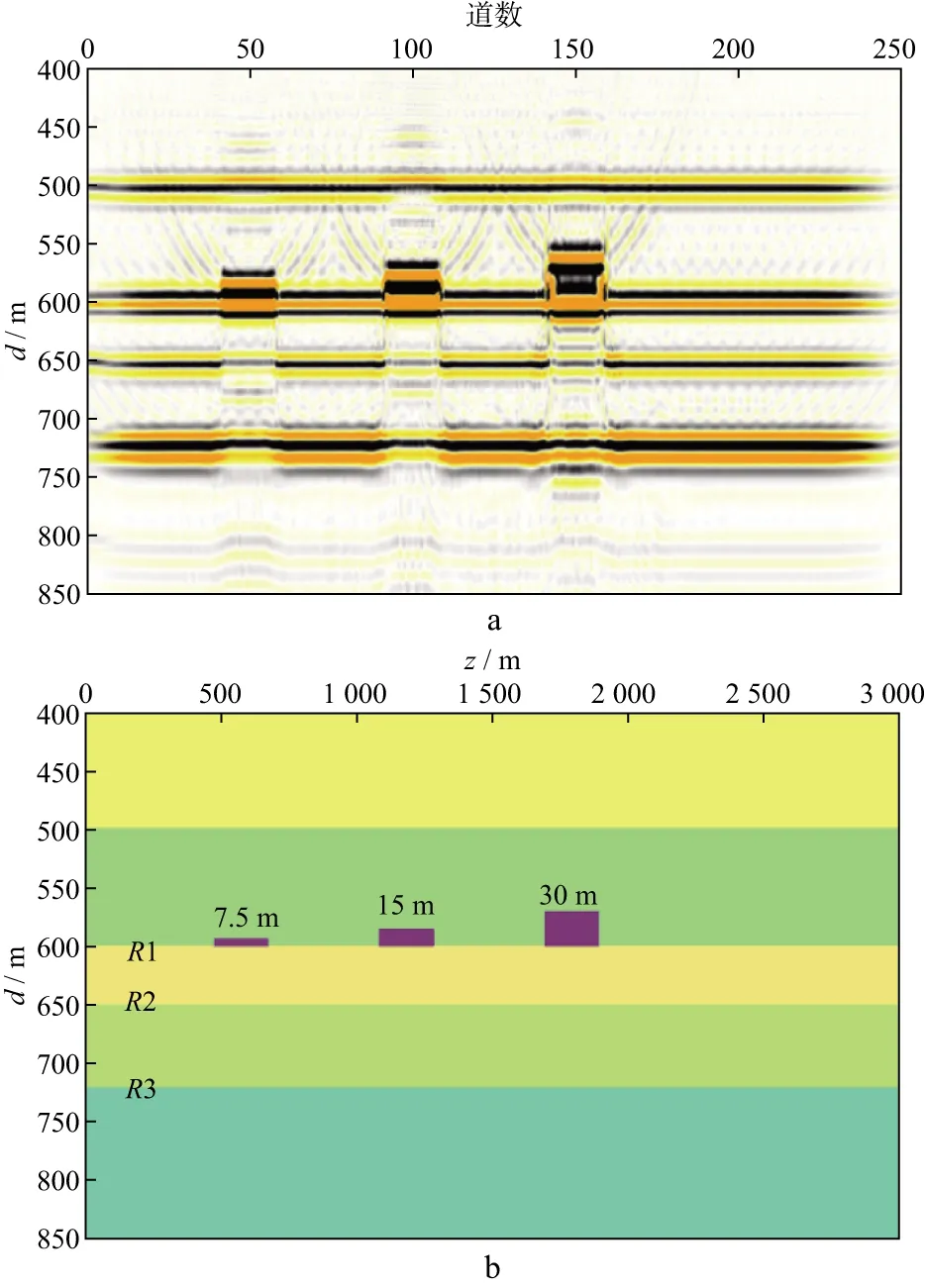
图6 含不同厚度底砾岩的RTM深度剖面(a)及其对应的速度模型(b)

图7为对图6a中含不同厚度底砾岩的RTM深度剖面沿层统计的振幅曲线,图7a至图7c分别为反射界面R1,R2,R3的沿层统计的振幅曲线。分析振幅曲线可知,反射界面R1在底砾岩区域出现了强振幅特征;在底砾岩下方的反射界面R2,R3的振幅曲线中出现了3个振幅屏蔽的区域,其屏蔽强度与厚度呈正相关,同一反射界面屏蔽的幅度随着底砾岩厚度的增加而增大,最大可达35%。

图7 对图6a中含不同厚度底砾岩的RTM深度剖面沿层统计的振幅曲线a R1; b R2; c R3

2.4 不同底砾岩层数

图8为含不同层数底砾岩的RTM深度剖面及其对应的速度模型,3组底砾岩的其它参素相同,层数从左到右依次为1层、2层、4层,通过改变底砾岩的层数研究其对振幅屏蔽的影响程度。

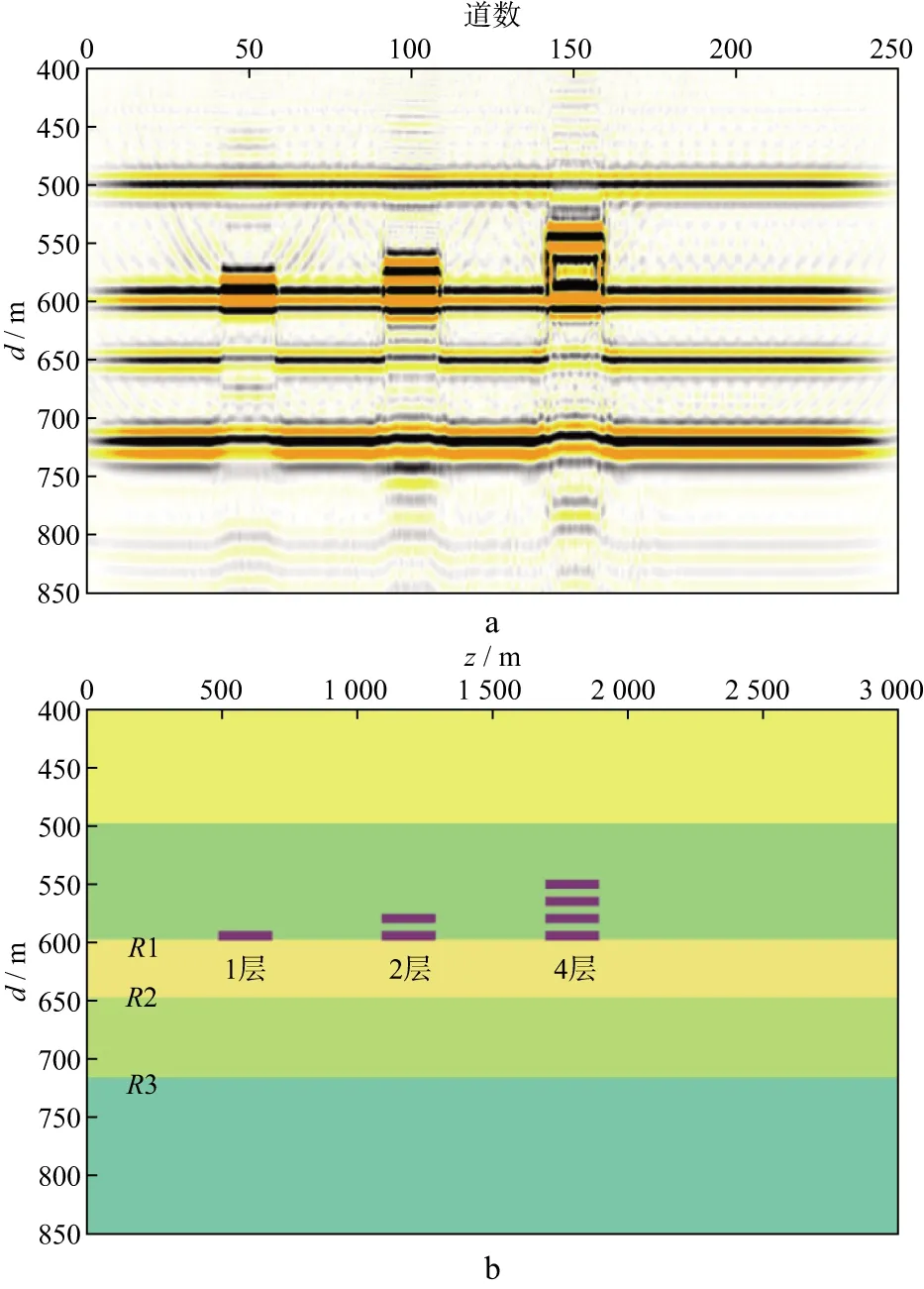
图8 含不同层数底砾岩的RTM深度剖面(a)及其对应的速度模型(b)

图9为对图8a中含不同层数底砾岩的RTM深度剖面沿层统计的振幅曲线,图9a至图9c分别为反射界面R1,R2,R3的沿层统计的振幅曲线。分析振幅曲线的形态可知,R1振幅曲线上出现的3个振幅增强的区域为反射界面R1在底砾岩区域的强振幅响应,其振幅增强的幅度和范围相同;在底砾岩下方的反射界面R2,R3的振幅曲线中,分别出现3个振幅减弱的区域,沿层统计振幅可知,同一反射界面屏蔽的幅度随着层数的增加而增大,对下伏地层振幅的屏蔽程度最高可达75%。

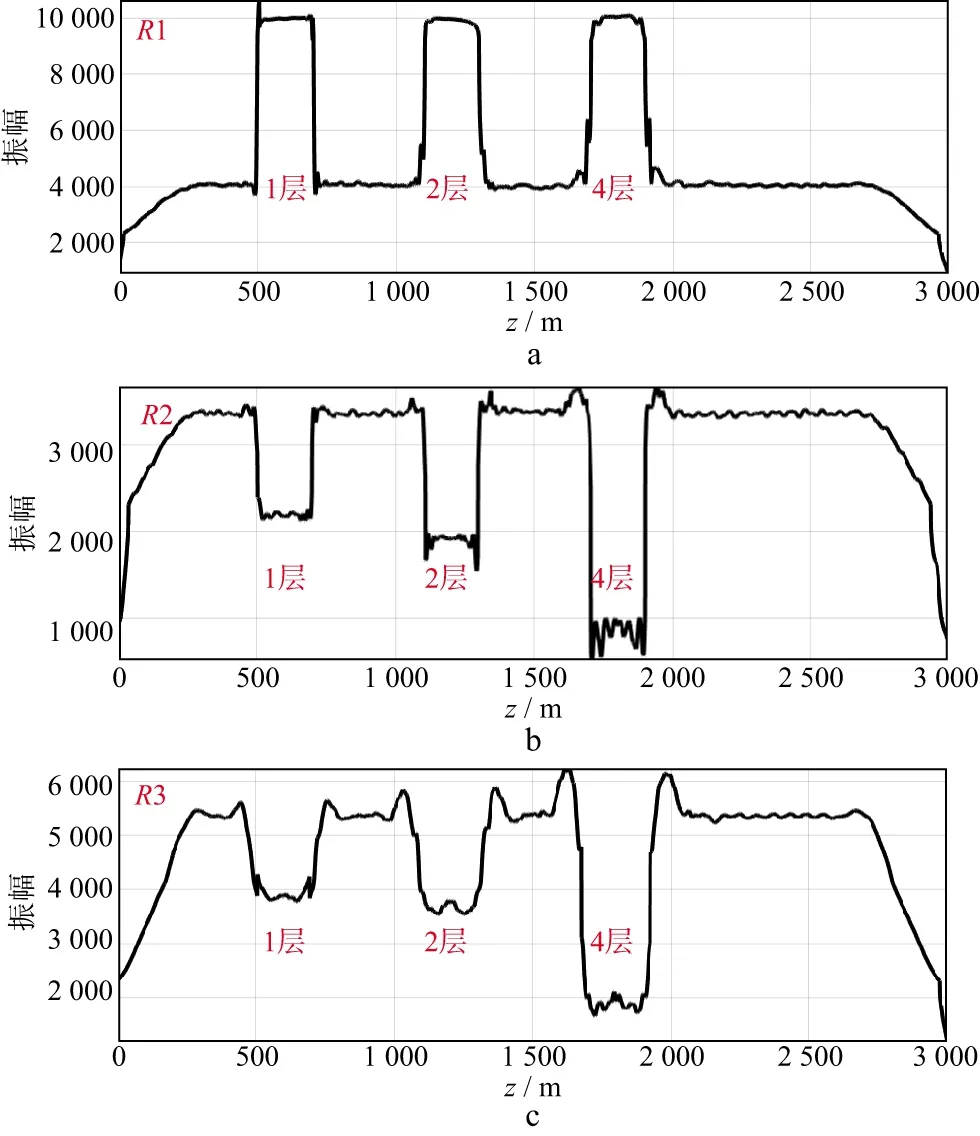
图9 对图8a中含不同层数底砾岩的RTM深度剖面沿层统计的振幅曲线a R1; b R2; c R3

2.5 不同底砾岩速度

图10为含有不同速度底砾岩的RTM深度剖面及其对应的速度模型,3组底砾岩的其它参数相同,速度从左到右依次为3500,4500,5500m/s,通过改变底砾岩的速度,研究其对振幅屏蔽的影响程度。

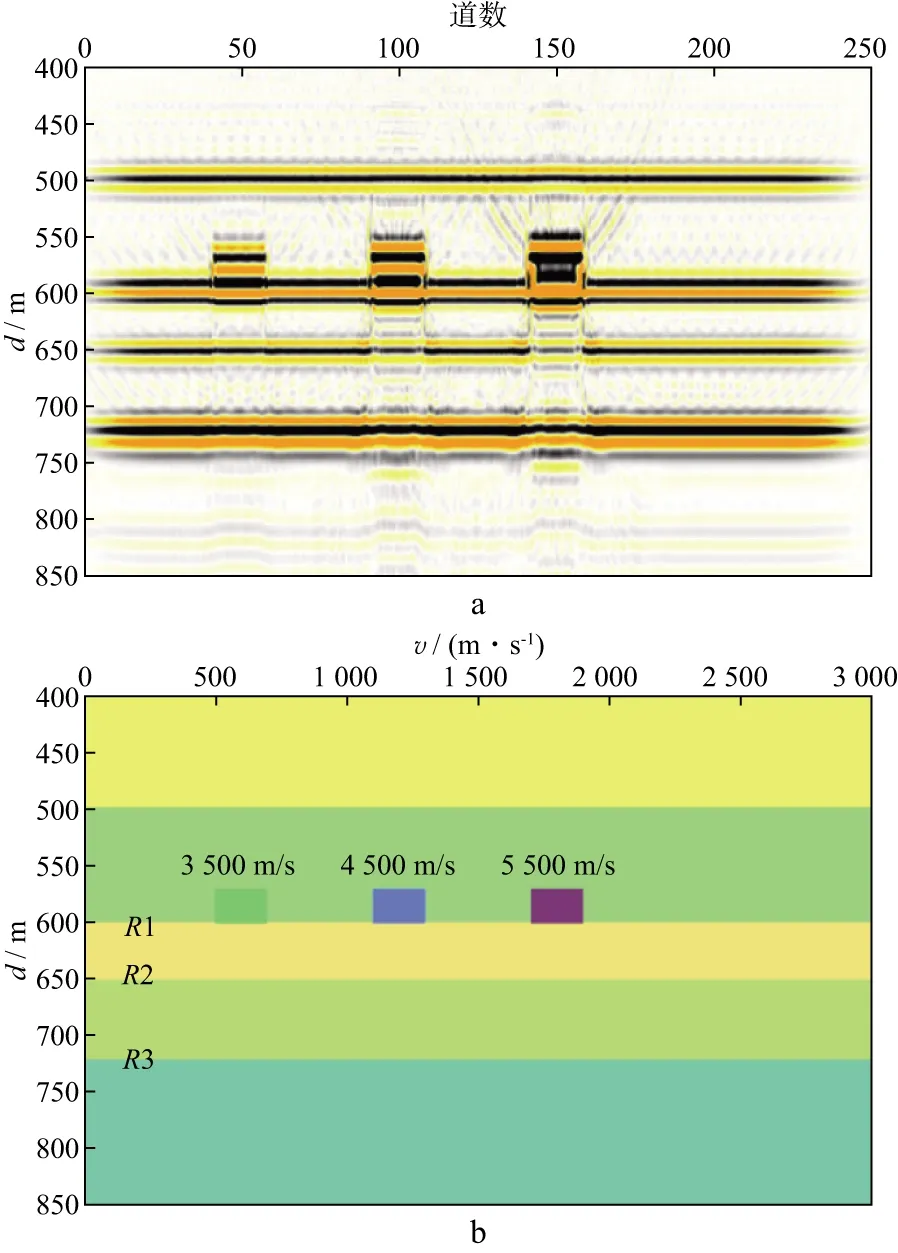
图10 含不同速度底砾岩的RTM深度剖面(a)及其对应的速度模型(b)

图11为对图10a中含不同速度底砾岩的RTM深度剖面沿层统计的振幅曲线,图11a至图11c分别为反射界面R1,R2,R3的沿层统计的振幅曲线。分析可知,R1振幅曲线上的3个振幅增强的区域为反射界面R1在底砾岩区域的强振幅响应,振幅增强的范围相同但增强的幅度与底砾岩速度呈正相关;在底砾岩下方的反射界面R2,R3振幅曲线中,由于受到振幅屏蔽作用的影响出现了3个振幅低值区域,从振幅统计值可以看出,屏蔽的幅度随着速度的增加而变大,屏蔽强度最高可达60%。

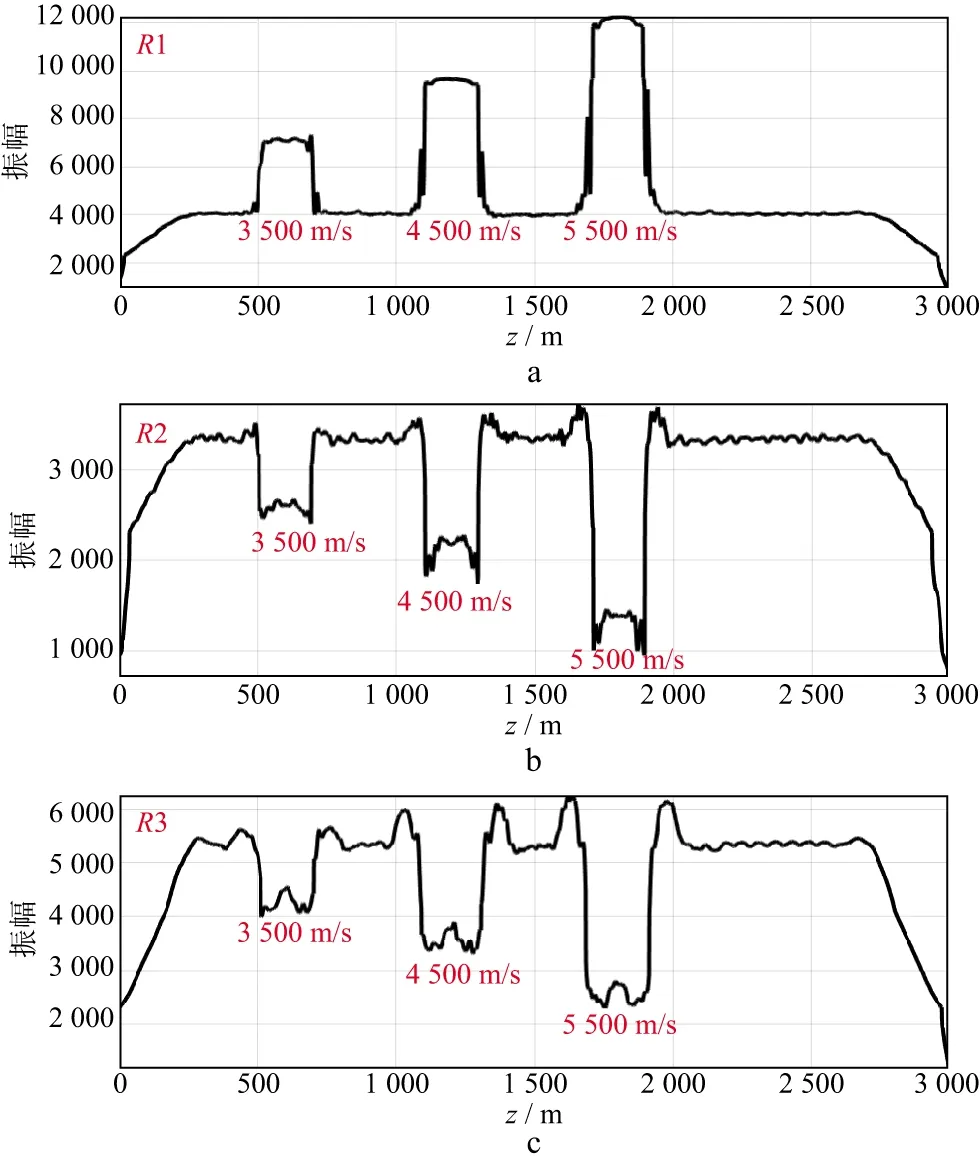
图11 对图10a中含不同速度底砾岩的RTM深度剖面沿层统计的振幅曲线a R1; b R2; c R3

3 强振幅屏蔽补偿方案及应用

3.1 扩大照明范围

研究发现地震反射波能量在入射角接近临界角处突然增强[19],采用大偏移距接收地震波场,可有效削弱屏蔽效应的影响,从而达到提高屏蔽层下反射波能量的目的。如图12所示的正演速度模型,长6000m,深1000m,除底砾岩外,其它地层参数与表1所示相同。中部含有4层长为200m,厚为7.5m的多层底砾岩构造,其速度为5500m/s。采用短、中、长3种不同的排列长度进行正演观测,其中炮间距和道间距均为25m;保持3种排列检波点数量相同,检波点布设范围为0～6000m,每炮均有241个接收点接收。短、中、长3种排列的不同点在于:炮点数分别为51炮、101炮、151炮,炮点布设范围分别为2375～3625,1750～4250,1125～4875m,最大偏移距分别为3625,4250,4875m。排列的照明范围随着偏移距的增大而增大,因此短、中、长3种排列的照明范围逐渐增大,其中反射界面R1,R2,R3分别为高速底砾岩下伏由浅到深的3个反射界面。对上述模型正演得到的炮集数据进行逆时偏移成像处理,得到RTM深度剖面。图13为不同排列长度正演数据的RTM深度剖面,图13a至图13c分别为51炮激发的短排列、101炮激发的中排列、151炮激发的长排列RTM深度剖面。对图13中3种排列长度下得到的RTM深度剖面中的同相轴R3(具体位置见图13中标注)进行沿层振幅统计,经过归一化处理后,可得如图14 所示的R3沿层统计的振幅曲线,其中黑、红、蓝3种颜色曲线分别表示51炮短排列、101炮中排列、151炮长排列的沿层振幅曲线。综合分析图13和图14 可以看出,随着照明范围的增加高速底砾岩下几套受强振幅屏蔽影响的反射轴振幅得到了提升,整个反射界面的能量也随着照明范围的增加变得更加均匀。对不同照明度下得到的结果进行正演及分析,可以得出如下结论:在地震采集过程中,扩大观测系统的照明范围,并采用大偏移距的采集方式,可以在一定程度上降低底砾岩对下伏地层的振幅屏蔽作用。

图12 含底砾岩正演速度模型及观测系统满覆盖范围分布

图13 不同排列长度正演数据的RTM深度剖面a 51炮短排列; b 101炮中排列; c 151炮长排列

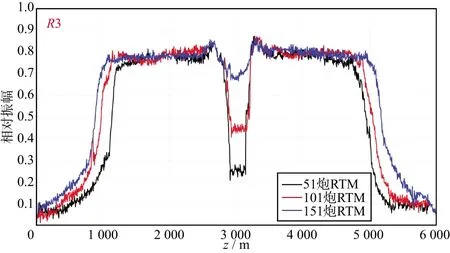
图14 不同排列长度RTM深度剖面中R3沿层统计的振幅曲线

3.2 Q-RTM成像技术

基于波动方程的逆时偏移(Qreverse time migration,Q-RTM)技术作为一种“保幅偏移”技术,能够更加精确对地下介质进行成像[20]。图15为图12 中所示不同排列长度正演数据的Q-RTM深度剖面。对图15中3种排列长度的Q-RTM剖面中的同相轴R3(具体位置见图15中标注)进行沿层振幅统计,可得如图16所示的R3沿层统计的振幅曲线,其中黑、红、蓝3种颜色曲线分别表示51炮短排列、101炮中排列、151炮长排列的沿层振幅曲线。将三种不同排列下的Q-RTM成像剖面(图15)与RTM成像剖面(图13)进行对比分析可知,根据剖面中底砾岩下伏地层所呈现的波组特征,可以看到在相同排列下,Q-RTM成像结果比RTM成像结果受振幅屏蔽的影响更小,底砾岩下伏地层能量也更加均匀。定量对比分析Q-RTM深度剖面的沿层统计的振幅曲线(图16)和RTM深度剖面的沿层统计的振幅曲线(图14)可知,在相同排列下,Q-RTM深度剖面中屏蔽区域的同相轴振幅被屏蔽掉的能量弱于相应位置处的RTM结果,其中短排列振幅屏蔽比例降低33%,中排列降低26%,短排列降低9%。

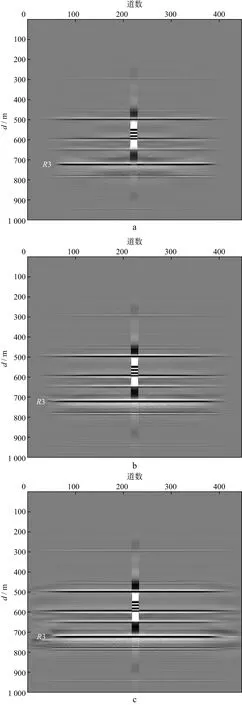
图15 不同排列长度正演数据的Q-RTM深度剖面a 51炮短排列; b 101炮中排列; c 151炮长排列

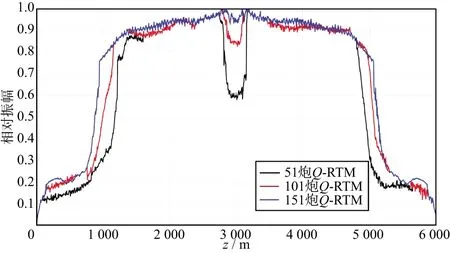
图16 对图15中3种排列长度Q-RTM偏移剖面R3沿层统计的振幅曲线

在正演模拟分析结果的指导下,将Q-RTM技术应用于海上某工区实测地震数据的处理,较好地解决了高速底砾岩对下伏地层振幅的屏蔽作用。图17a为实测地震数据经过深度域层析反演得到的速度模型,黑色箭头为底砾岩赋存位置,反演结果显示其速度约为3500m/s,与围岩速度(2500m/s)差异较大,呈现为典型的高速异常体特征。图17b为实测地震数据反演得到的Q模型,其反演过程如下:拾取叠后地震资料的目的层,结合频谱分析结果,利用多道加权频谱比法估算层Q值,建立初始Q值模型。在初始Q值模型的基础上,利用基于道集频谱一致性的Q值层析反演方法,进一步建立了如图17b所示的更为精细的Q模型。

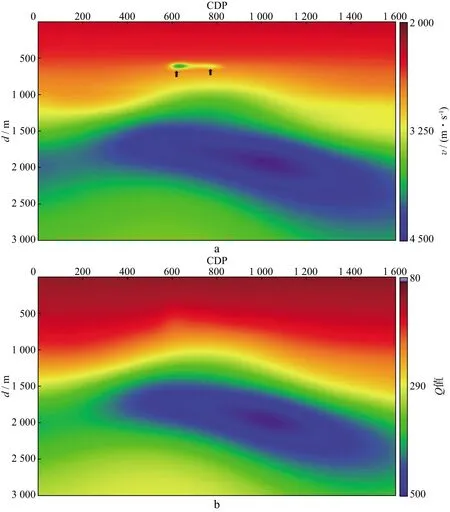
图17 实测地震数据经过深度域层析反演得到的速度模型(a)及Q模型(b)

依据图17a所示的速度模型,对实测地震数据进行RTM偏移,选取CDP600～800范围内的局部偏移成像结果(图18a)。同时,基于速度模型和Q模型,对相同的地震数据进行Q-RTM,选取相同范围偏移结果(图18b)。如图18a中RTM剖面所示,黑色箭头处呈现高速底砾岩的强反射特征;红色箭头处出现其下伏地层受到振幅屏蔽以后呈现出的弱振幅及不连续的反射特征。在图18b中红色箭头所示的受屏蔽效应影响的位置,其下伏地层振幅强度及同相轴的连续性都得到了明显的改善,振幅屏蔽效应得到了有效削弱,为后续的地震资料解释工作提供了更为合理的数据。

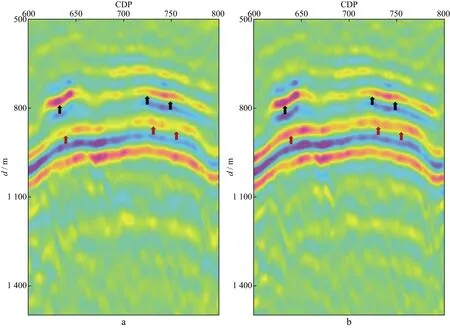
图18 底砾岩屏蔽区RTM(a)及Q-RTM深度偏移(b)剖面

4 结论及认识

根据本文正演模拟数据的分析结果及相关处理技术的应用结果,得到以下结论。

1) 底砾岩的厚度、层数、速度与强振幅屏蔽呈正相关,参数值越高屏蔽强度越大;下伏地层随着深度的增加受强振幅屏蔽影响减弱;底砾岩自身长度对强振幅屏蔽程度无明显影响,但随着长度的增加,其屏蔽范围会随之增加。通过对以上因素的分析可知,底砾岩对下伏地层振幅影响程度的因素由大到小排序分别为:速度、层数、厚度、埋深和长度。

2) 通过增大地震观测系统排列长度,从而增加底砾岩下伏地层的照明强度,从地震数据采集的角度,解决高速底砾岩对下伏地层的“振幅屏蔽”效应。

3) 采用Q-RTM技术,在一定程度上可以对受到“振幅屏蔽”影响的地层进行振幅补偿。

在实际地震勘探中,底砾岩自身物性特征及分布规律较为复杂,导致影响振幅屏蔽效应强弱的因素也需要进行综合评估,同时在振幅补偿方面,单一的补偿技术并不能较好地解决振幅屏蔽的影响,应从采集、处理、解释等不同角度,采用综合性的补偿方法。后续应加强振幅屏蔽理论方面的研究,尤其是基于非均匀介质和复杂底砾岩构造下的波场传播及反射特征研究,从根源上为强振幅屏蔽补偿技术的研发提供理论支撑。