灰狼与郊狼混合优化算法及其聚类优化
张新明 姜云 刘尚旺 刘国奇 窦智 刘艳
在现实世界中,无时无处无不面临着优化问题.随着社会的发展,急需处理的优化问题越来越多样化并越来越复杂.而诸如牛顿法、梯度下降法等传统的方法不能够很好地处理这些急需解决的优化问题.因此,许多研究者建立了各种仿生类的智能计算模型,提出了许多智能优化算法.群智能优化算法(Swarm intelligence optimization algorithm,SIOA)是模拟自然界社会群体集体行为的一种智能优化方法[1],包括粒子群优化(Particle swarm optimization,PSO)算法[2]、灰狼优化算法(Grey wolf optimizer,GWO)[3]、郊狼优化算法(Coyote optimization algorithm,COA)[4]等.SIOA 具有易于实现、能有效处理全局优化和大规模优化问题等优势,广泛应用于多目标优化、数据聚类以及模式识别等诸多领域[5].但根据无免费午餐定理[6],没有任何一种SIOA 能独立地解决所有的优化问题,每种SIOA 都有自身的优势和局限性.因此许多学者提出了大量新奇和改进的SIOA,其中包括算法的混合改进.两种或多种算法的混合可以达到优势互补,以获得最佳的优化性能[7].
GWO 是由Mirjalili等[3]于2014 年提出的一种新颖的SIOA,具有原理简单、开采能力强、可调参数少等优点,但存在易陷入局部最优、解决复杂优化问题性能差等缺点.因此许多学者对其进行了研究和改进,其中包括混合改进.例如张新明等[7]提出一种GWO 与人工蜂群算法的混合算法,其中在人工蜂群观察蜂阶段自适应融合GWO,以便增强开采能力和提高优化效率.Zhang等[8]提出一种基于生物地理学优化算法和GWO的混合算法,将改进的基于生物地理学优化算法和基于反向学习的GWO 混合,使得优化性能最大化.Teng等[9]提出一种PSO 与GWO 结合的混合算法,该算法具有更好的寻优能力和更强的鲁棒性.Arora等[10]提出一种乌鸦搜索算法与GWO的混合算法,更有效地实现了全局优化.
COA 是由Pierezan等[4]于2018 年提出的一种模拟郊狼群居生活、成长、生死等现象的新型SIOA.COA 具有独特的搜索模型和结构以及出色的优化能力,尤其在解决复杂优化问题优势明显,但仍存在搜索效率低、可操作性不强以及收敛速度慢等缺陷,且由于COA 提出的时间较短,需改进和完善并拓展其应用领域.鉴于GWO 和COA 各有优势和不足,本文将两种算法分别进行改进和简化,得到改进的COA (Improved COA,ICOA)和简化的GWO (Simplified GWO,SGWO),然后通过正弦交叉策略将ICOA 和SGWO 有机融合在一起,从而获得了一种性能优越且高效的混合COA (Hybrid COA with GWO,HCOAG).另外,混合算法的研究一直是优化领域的热点,因此研究GWO 与COA的混合是一项较有意义的工作.
1 灰狼优化算法
GWO 模拟了自然界中灰狼种群严格的社会等级制度和群体捕食行为.在其社会等级制度中,灰狼从高到低依次为α,β,δ,ω狼.其捕食行为是追踪和接近猎物、追捕和包围猎物、攻击和捕杀猎物.GWO 将狼群中的α,β,δ,ω狼的位置分别代表第一最优解、第二最优解、第三最优解和候选解.灰狼包围行为的数学模型为
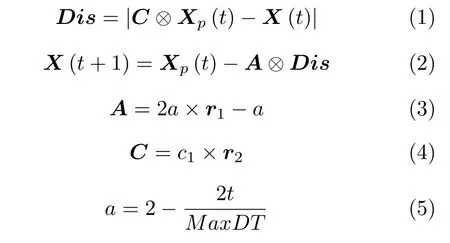
其中,Dis是灰狼与猎物间的距离,t是当前迭代次数,Xp是猎物的位置向量,X是灰狼的位置向量.A和C是系数向量.系数a在迭代过程中从2线性递减到0,MaxDT是最大迭代次数,r1和r2是[0,1]中的均匀分布随机向量,c1为可调参数[11],⊗表示两个向量各个对应的分量相乘.狩猎行为的数学模型为
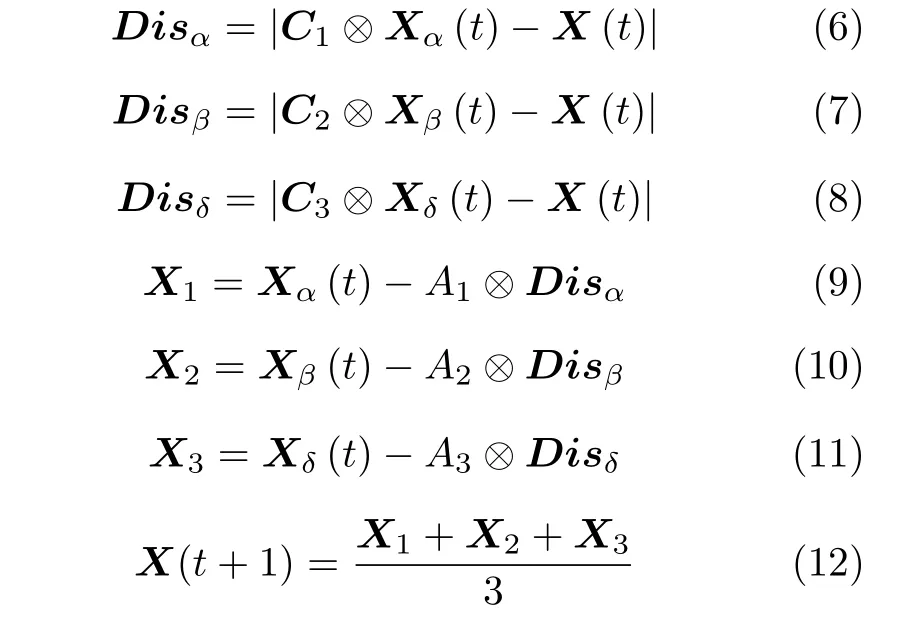
其中,Disα,Disβ和Disδ分别表示当前狼与3 头最优灰狼间的距离.式(12)代表ω狼在α,β和δ狼的引导下移动的新位置,即GWO 产生的新解.GWO的流程图见图1.
从上述描述和图1 可知,与PSO 等经典的SIOA 相比,GWO的主要特点有:1)GWO 采用3 头最优狼(最优解)引导ω狼围猎,有较强的局部搜索能力,但在解决复杂优化问题时,容易陷入局部最优;2)GWO 仅有两个参数a和c1,前者采用动态调整方式,后者c1常取常数2,调整的参数少,故可操作性强;3)原理简单、易于实现,但更新是基于维的计算,需计算式(6)~(12),故计算复杂度较高;4)目标函数采用并行计算方式,故运行速度较快.
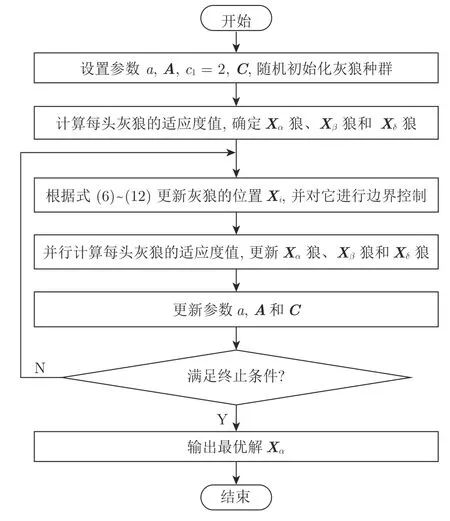
图1 GWO的流程图Fig.1 Flow chart of GWO
2 郊狼优化算法
COA 包含初始化参数和狼群、组内郊狼成长、郊狼生与死和被组驱离与接纳[4]等4 个主要步骤.
2.1 参数初始化和随机初始化郊狼群组
首先设置参数,如郊狼群规模N,郊狼组数Np,组内郊狼数Nc和MaxDT等,其中,N=Nc×Np.然后随机初始化郊狼群组,第p组第c个郊狼第j维的随机化操作如式(13).最后计算每头郊狼soc的社会适应度值fit,如式(14).
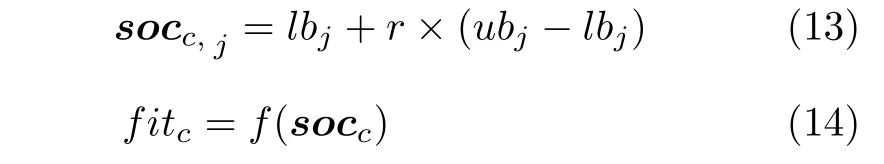
其中,lbj和ubj分别表示郊狼第j维社会状态因子的下界和上界,j=1,2,···,D,D为搜索空间的维度,r为[0,1]内均匀分布的随机数,f表示适应度函数.
2.2 组内郊狼成长
组内最优狼alpha、组文化趋势cult以及随机选取的两头郊狼cr1和cr2影响组内郊狼的成长过程,即组内郊狼成长受δ1和δ2的影响.其中cult的计算如式(15)所示,即其每一个因素是组内所有郊狼对应社会因子的中位数(O为排名后的社会因子序列),故cult又称中值郊狼.δ1和δ2计算见式(16)和式(17),郊狼的成长方式见式(18).
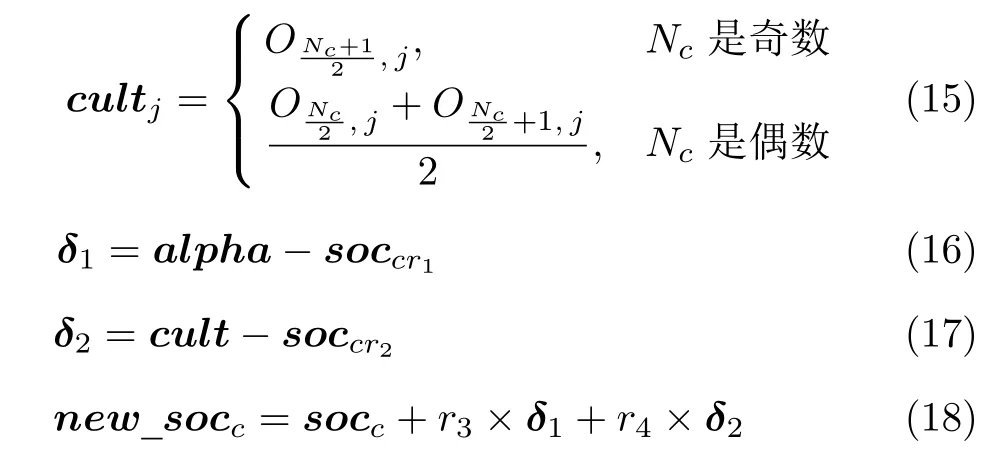
其中,new_socc是组内第c头郊狼成长获得的新解,r3和r4是[0,1]内均匀分布的随机数.组内的郊狼成长后评估其社会适应能力如式(19)所示,new_fitc为新适应度值.
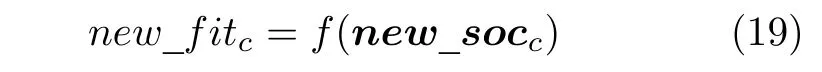
最后采用迭代贪心算法进行优胜劣汰(式(20)),如此新产生的更优郊狼参与组内其余郊狼成长以加快收敛速度.

2.3 郊狼生与死
幼郊狼 (pup)的诞生受随机选择父母郊狼的遗传基因和环境因素的影响,见式(21)所示.

其中,rj是均匀分布在[0,1]内的随机数;j1和j2是两个随机选择的维度标号,以确保两个父郊狼的基因能够遗传给幼狼;Rj是在第j维决策变量范围内随机产生的变异值;Ps和Pa分别是分散概率和关联概率,它们决定着幼狼被遗传和变异的情况,如式(22)和式(23)所示.
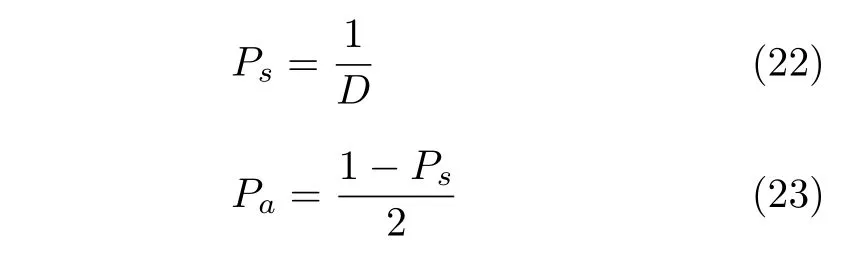
幼狼出生后,评估其社会适应能力,并依照其能力决定生与死,具体描述如下:在社会适应能力上,1)组内只有一个郊狼比幼狼差时,则此郊狼死亡,幼狼存活,并设它的年龄为0,即age=0;2)组内有多个郊狼比幼狼差时,能力差且年龄最大的郊狼死亡,幼狼存活,并设age=0;3)组内所有郊狼都比幼狼强时,幼狼死亡.
2.4 郊狼被驱离和接纳
在COA 中,郊狼以Pe的概率被组驱离和接纳.郊狼初始被随机分配到组群中,但有时某些郊狼会离开它所在组群而加入另一组群,这种随机驱离和接纳用来保证组内郊狼的多样性和组间信息共享,Pe的计算方式为

COA的伪代码如算法1 所示.
算法1.COA 算法

从以上描述可知,与PSO 等经典的SIOA 相比,COA的主要优势有:1)具有很好的搜索框架,即多组结构,郊狼随机被组驱离和接纳等使郊狼群具有多样性,有较强的探索能力,能够更好地解决复杂优化问题[12];2)组内最优郊狼和组内文化趋势引导组内每个郊狼的成长,增强了局部搜索能力;3)郊狼组内的生与死受随机选择父郊狼的遗传因子和环境变异因子影响,郊狼生与死算子使得COA具有一定的全局搜索能力.其主要不足有:1)结构复杂,计算复杂度高;2)采用迭代贪心算法,稳定性差,效率低;3)需调整的参数多,如Pe,Np和Nc等需调整,可操作性差;4)多组结构等虽然增强了探索能力,但组与组之间信息共享不足,导致搜索后期收敛速度慢.
3 灰狼与郊狼混合优化算法
3.1 提出HCOAG的动机
COA 与GWO 虽然同属狼群算法,但二者有许多不同.如在搜索方式上,前者模拟郊狼的成长、生与死,而后者模拟灰狼的等级制度和狩猎模式;在引导上,前者仅仅使用一头最好的狼来引导其它狼成长,而后者使用3 头最优狼来引导其它狼搜索;在结构上,前者复杂,后者简单;在产生新解方式上,前者有两种方式,后者只有一种方式等等.因此,COA 和GWO 各有优势和不足.为了弥补二者不足,本文将COA 和GWO 两种狼群算法经过改进后进行了有机结合,从而获得一种性能优越且高效的混合算法(HCOAG).
3.2 改进的郊狼优化算法
ICOA 主要包括高斯全局趋优成长算子和动态调整组内郊狼数方案.
3.2.1 高斯全局趋优成长算子
为了提高郊狼成长后的社会适应能力、组与组之间的信息共享程度及算法收敛速度,受Omran等[13]提出的全局最优和声搜索算法中趋优策略及高斯分布的启发,对其组内郊狼成长方式进行改进,提出一种高斯全局趋优成长算子.全局趋优算子充分利用郊狼种群当前全局最优郊狼的状态信息,使郊狼成长向当前全局最优郊狼趋近,提高开采能力,也使得组内信息经全局最优解达到组间共享.高斯分布又称为正态分布,与COA的均匀随机分布[0,1]相比,可以增加搜索范围,在一定程度上增强全局搜索能力.
在组内郊狼成长过程中,在式(18)中引入趋优算子和高斯分布随机因子,具体见式(25)和式(26).
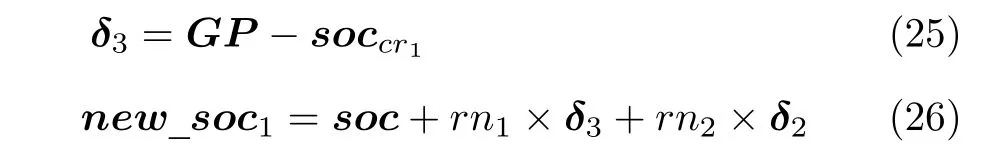
式(25)中,GP为当前全局最优郊狼的状态,δ3表示组内随机选取的一个郊狼状态 (cr1)与GP的差值.式(26)中,rn1和rn2是均值为0、方差为1的高斯(正态)分布产生的随机数,new_soc1表示每头郊狼在δ2和δ3的共同作用下成长产生的新状态(新解).
从式(25)和式(26)可以看出,与COA 相比,在搜索前期,个体间差异大,缩放因子(高斯随机数)变化范围大,故增强了探索能力.在搜索后期,虽然还是采用高斯随机数,但个体间差异小,δ2和δ3的值变小,故搜索范围变小,强化开采能力.且由于采用全局最优解引导,故更增强了开采能力,同时上一组获得的全局最优解,会作用于下一组的郊狼成长,如此形成一种信息共享的正反馈作用,大幅度加快了收敛速度.另外,所有组内郊狼成长后并行计算它们的适应度值和优胜劣汰,提高了运行速度和稳定性.
3.2.2 动态调整组内郊狼数方案
如上文所述,COA 有多个参数需要调整,可操作性差.对于以上改进的COA,主要有两个参数Nc和Np对优化性能影响较大.在N固定下,如果Nc确定,则Np=N/Nc,即Np越大,Nc越少,成长操作少,但全局解的作用逐组增强,开采强;反之,成长操作多,Np少,全局解的作用减弱,开采弱.为了提高COA的可操作性,本文对Np和Nc参数进行动态调整.设N=100,则Np和Nc必须为100的因子,依据文献[4],每组郊狼数不能超过14,所以Nc只能为4、5 和10.由于Nc不能少于3,这是因为组内郊狼成长至少需要3 头郊狼,包括随机选取的两头郊狼和组内最优郊狼.当Nc=4 时可选郊狼范围受限制,所以Nc最可能的取值为5 和10,故具体的分配方式如图2 所示,动态调整参数方案如算法2 所示.
图2 组数 N p 与组内郊狼数 N c的分配图Fig.2 Disposition graph of two parameters N c andNp
算法2.动态调整参数Nc和Np

在搜索后期,Nc=5,则Np=20,组数多,增强全局解的正反馈作用,局部搜索能力增强;在搜索前期,Nc=10,则Np=10,组数少,减弱全局解的正反馈作用,全局搜索能力增强.因此,动态调整组内郊狼数参数不仅提高了可操作性,而且可以更好地平衡探索与开采能力.另外,在动态调整参数之后,随机分组,如此可以省去郊狼被组驱离与接纳这个过程,从而不需要调整参数Pe,因此提高了可操作性.
3.3 简化的灰狼优化算法
为了进一步解决COA 存在搜索效率低和易陷入局部最优的问题,本文引入GWO 搜索方式.首先提出一种精简的GWO 搜索方式,即将式(6)~(11)与COA 组内郊狼进行融合并简化,具体如式(27)~(29).

其中,tempc表示当前组第c个郊狼的状态.NX1,NX2和NX3表示组内郊狼分别在GP,alpha和cult的引导下获得成长的情况.从式(27)~(29)可以看出,这3 个式子去掉了式(6)~(8)中的可调参数向量C,保留GWO的优势并克服其不足,即在SGWO 中,去掉C,无需调整c1,也省略了向量C的相关计算.所以,这种简化的GWO 在保证其有较强开采能力的同时,提高了可操作性并降低了计算复杂度.为了更进一步简化计算,SGWO 直接采用COA 中的当前全局最优郊狼、组内最优郊狼和中值郊狼(组内文化趋势)的引导寻找最优解,无需寻找组内的第二和第三最优郊狼,如此SGWO 与COA 达到了一种高效融合.为方便理解SGWO,关于GWO 中的灰狼等级情况与SGWO 中的等级情况的对比见图3 所示.
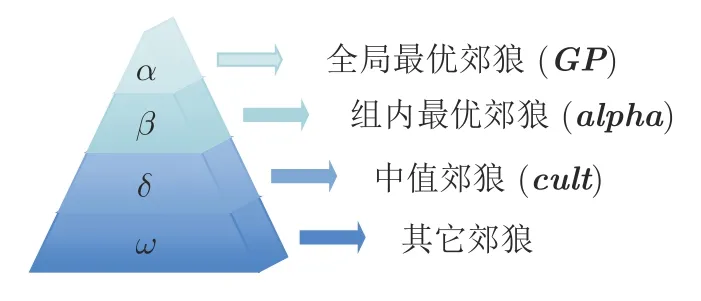
图3 GWO 与SGWO的等级情况对比Fig.3 Comparison of hierarchies of GWO and SGWO
3.4 正弦交叉混合策略
为了平衡COA 组内郊狼成长的探索与开采能力,本文采用正弦交叉策略将ICOA 与SGWO 有机混合.其中交叉策略是指在一定概率的情况下,两个解进行交叉得到一个新解.当概率为零时,两个解的维值不交换;当概率为1 时,两个解的维值全部交换,这两种情况都不能产生新解.因此只有概率为一个适当的值时,两个解的交叉效果才会达到最好.其中使用正弦函数概率模型使得探索和开采都有良好的表现,即使用正弦函数自适应控制交叉概率CR(在0.5 附近前期小幅度波动,后期大幅度跳动)可以兼顾组内郊狼的多样性和收敛性[14],其计算式为

本文采用的正弦交叉策略见算法3 所示,在rand<CR的概率下,组内第c个郊狼D维中一些维的值采用SGWO 搜索方式获取;反之,组郊狼的第c个郊狼D维中的其余维值采用高斯全局趋优成长算子获取.这种交叉策略具有如下特点:1)增强了组内各类郊狼的信息交流;2)交叉两个新解,二者的信息融合获得有别二者的新解,增强了新解的多样性,降低陷入局部最优的概率;3)前期在CR为0.5的附近小幅度波动,高斯全局趋优操作和GWO 操作以近似等概率的方式产生新解,多样性强,强化探索能力;后期在CR为0.5的附近大幅度跳动,如此产生的新解以其中一种操作为主,多样性降低,强化了开采能力.
算法3.正弦交叉策略

正弦交叉策略有机融合了两种搜索方式,很好地平衡了成长过程的探索与开采能力.HCOAG的流程图见图4.
从图4 可以看出,与COA 相比,HCOAG 主要有如下不同:1)成长方式采用正弦交叉策略融合高斯全局趋优方式和SGWO 方式;2)组内郊狼的适应度值采用并行计算;3)动态调整参数方案;4)丢弃了郊狼被组驱离与接纳的过程.

图4 HCOAG 流程图Fig.4 Flow chart of HCOAG
4 函数优化实验结果与分析
4.1 实验环境配置及参数设置
为验证HCOAG的有效性,本文采用经典基准函数和来自CEC2017的复杂函数进行优化实验.CEC2017 包括单峰函数(F1~F3)、多峰函数(F4~F10)、混合函数(F11~F20)和复合函数(F21~F30),详细情况见文献[15].实验环境采用主频3.00 GHz的Inter(R)Core(TM)i5-7400 CPU 和内存8 GB的PC 机,操作系统采用64 位的Windows 10,编程语言采用MATLAB2017A.选取的对比算法包括GWO[3]、COA[4]、MEGWO (Multi-strategy ensemble GWO)[16]、DEBBO (Differential evolution and biogeography-based optimization)[17]、HFPSO(Hybrid firefly with PSO)[18]、SaDE (DE with strategy adaptation)[19]、SE04 (Spherical evolution)[20]、FWA (Fireworks algorithm)[21]和TLBO(Teaching-learning based optimization)[22].MEGWO 是最近提出的GWO 改进算法,文献[16]表明它优于GWO 及其改进版以及其他的SIOA.DEBBO是DE 与BBO的混合算法,文献[17]表明它优于DE 和BBO 及其他优秀的SIOA.HFPSO 是PSO和FA的混合算法,文献[18]表明它优于PSO 和FA 等SIOA.SaDE 具有显著优秀性能,文献[19]表明SaDE 优于DE 等SIOA.SE04 是球形进化算法的变体之一,文献[20]表明SE04 显著优于GWO等算法.FWA 和TLBO 也是目前较为新型算法的代表.总之,这些对比算法具有较强的竞争性.
为公平起见,所有算法的公共参数设置相同.在CEC2017 上,依据文献[15]的参数最佳推荐,D=30,最大函数评价次数10 000 ×D,独立运行51 次.在经典函数的D=10 和D=30 上,MaxDT分别为100 和500,独立运行30 次.依据文献[4]的推荐,COA的最佳参数设置为:N=100,Nc=5,Np=20. HCOAG的N也设置为100,Np和Nc无需调整,算法其他参数采用相应文献中推荐的最佳设置.
一般单峰函数用来考察一个算法的局部搜索能力,多峰函数考察其全局搜索能力,混合和复合函数考察其处理复杂问题的能力.本文采用均值(Mean)和方差(Std)分别评估一个算法的优化性能和稳定性.在解决极小值问题中,均值越小表示算法性能越好,方差越小表示算法稳定性越好.另外,还采用了排名(Rank)方法.其评价标准是先比较算法获得的均值,均值越小算法名次越好;在均值相同的情况下,再比较方差,方差越小算法名次越好.结果表中的“Count”表示排名为第一的总次数,“Ave rank”表示平均排名情况,“Total rank”表示在“Ave rank”基础上的总排名情况,最优者用加粗字体表示.
4.2 与不完全算法的对比分析
为验证每个改进对HCOAG 优化性能的贡献,将HCOAG 与其不完全算法HCOAG5(Nc=5和Np=20的HCOAG)、HCOAG10(Nc=10和Np=10的HCOAG)、ICOA、SGWO、GWO 和COA 在CEC2017的30 维函数上进行实验,实验结果如表1 所示.
从表1 中可以看出,HCOAG5在单峰函数上获得最好的结果次数最多,表明Np增大,在提高郊狼生与死的全局搜索能力的同时,大幅度提高了COA的开采能力,即HCOAG5中高斯趋优成长和GWO 搜索都采用当前全局最优郊狼引导,不仅获得更好的全局最优解,这种全局最优解又作用于下一组郊狼的成长过程,如此形成正反馈机制:Np越大,开采越强,收敛速度越快.但容易陷入局部最优,如在多峰函数上的表现不尽人意.HCOAG10在多峰函数上表现出了良好的优化性能,表明Np变少,在提高组内郊狼成长的局部搜索能力的同时,正反馈减弱,开采能力降低,即陷入局部最优的概率也降低了.ICOA 中没有精简的GWO,整体来说优于COA,表明对COA的改进是有效的.SGWO在整体上优于GWO,表明SGWO 提高了GWO搜索能力.与GWO 相比,COA的优化性能更好,即COA 能更好地处理复杂优化问题.在7 个算法中,HCOAG的平均排名为2.20,COA、GWO、HCOAG5、HCOAG10、ICOA 和SGWO的平均排名分别为5.23、6.87、3.10、2.60、3.07 和4.93,总排名的名次分别为6、7、4、2、3 和5.在HCOAG 与6 种对比算法中,HCOAG 获得了最好的优化性能,这也说明本文提出的算法是有效的.
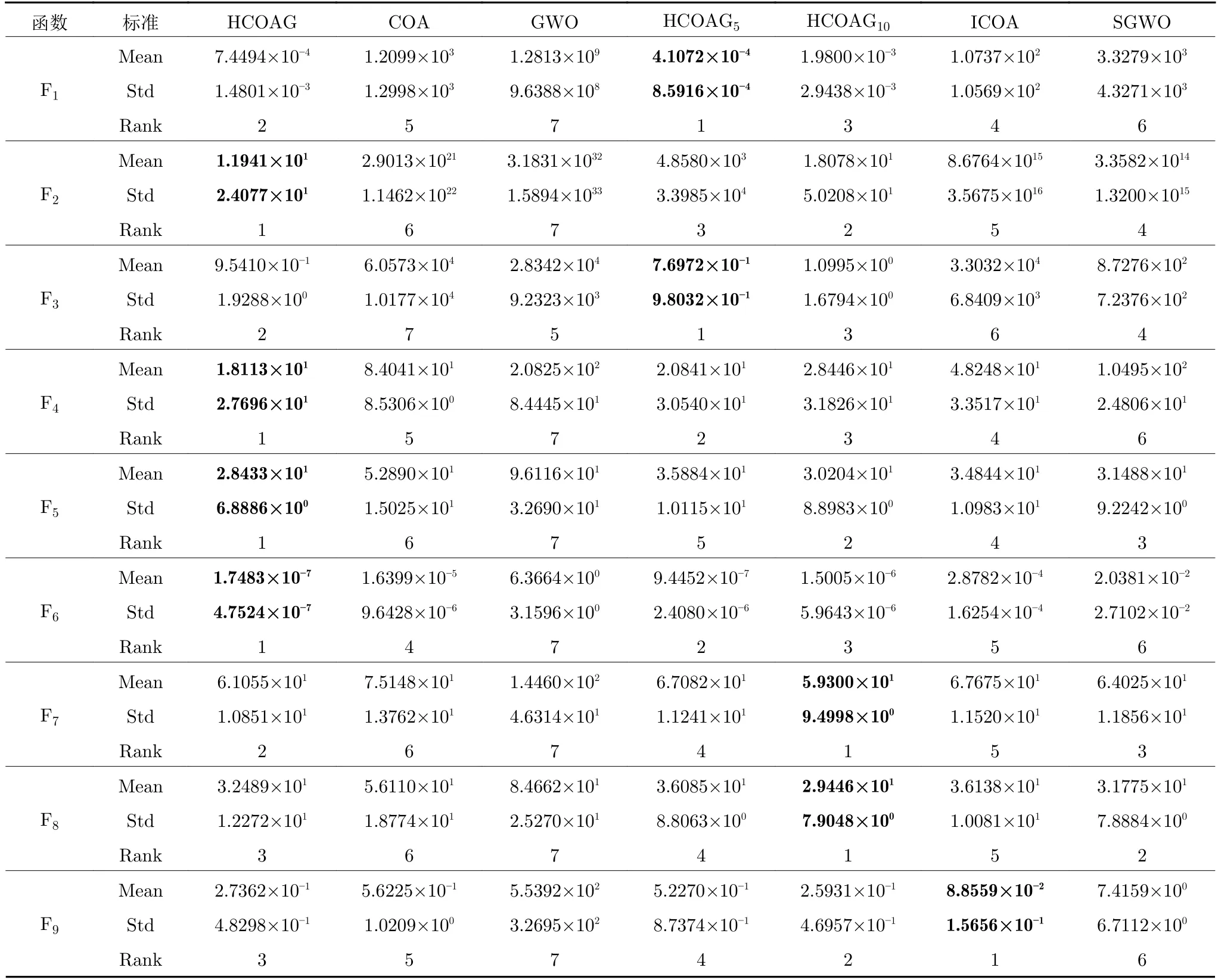
表1 HCOAG 与其不完全算法的结果对比Table 1 Comparison results of HCOAG and its incomplete algorithms
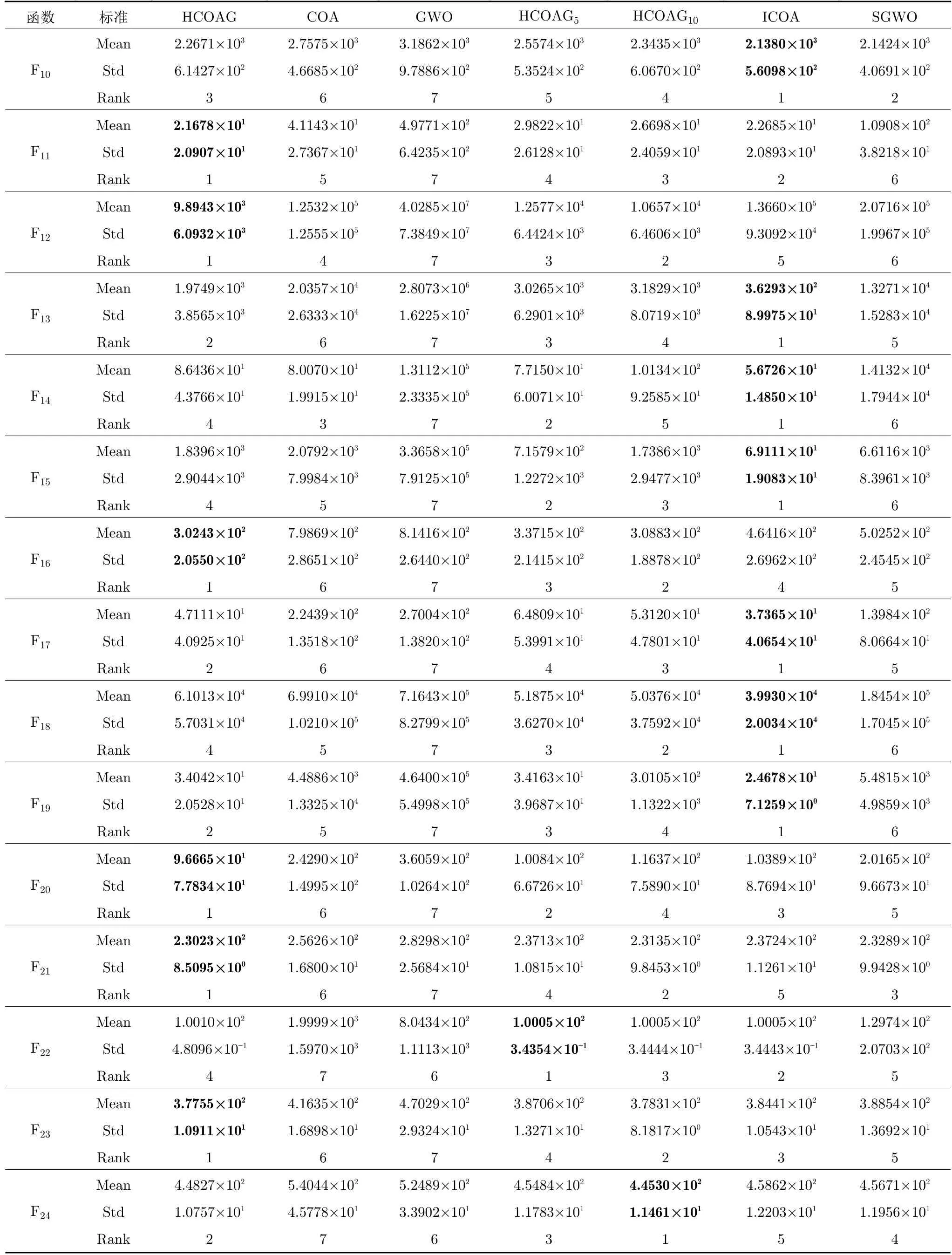
表1 HCOAG 与其不完全算法的结果对比 (续表)Table 1 Comparison results of HCOAG and its incomplete algorithms (continued table)
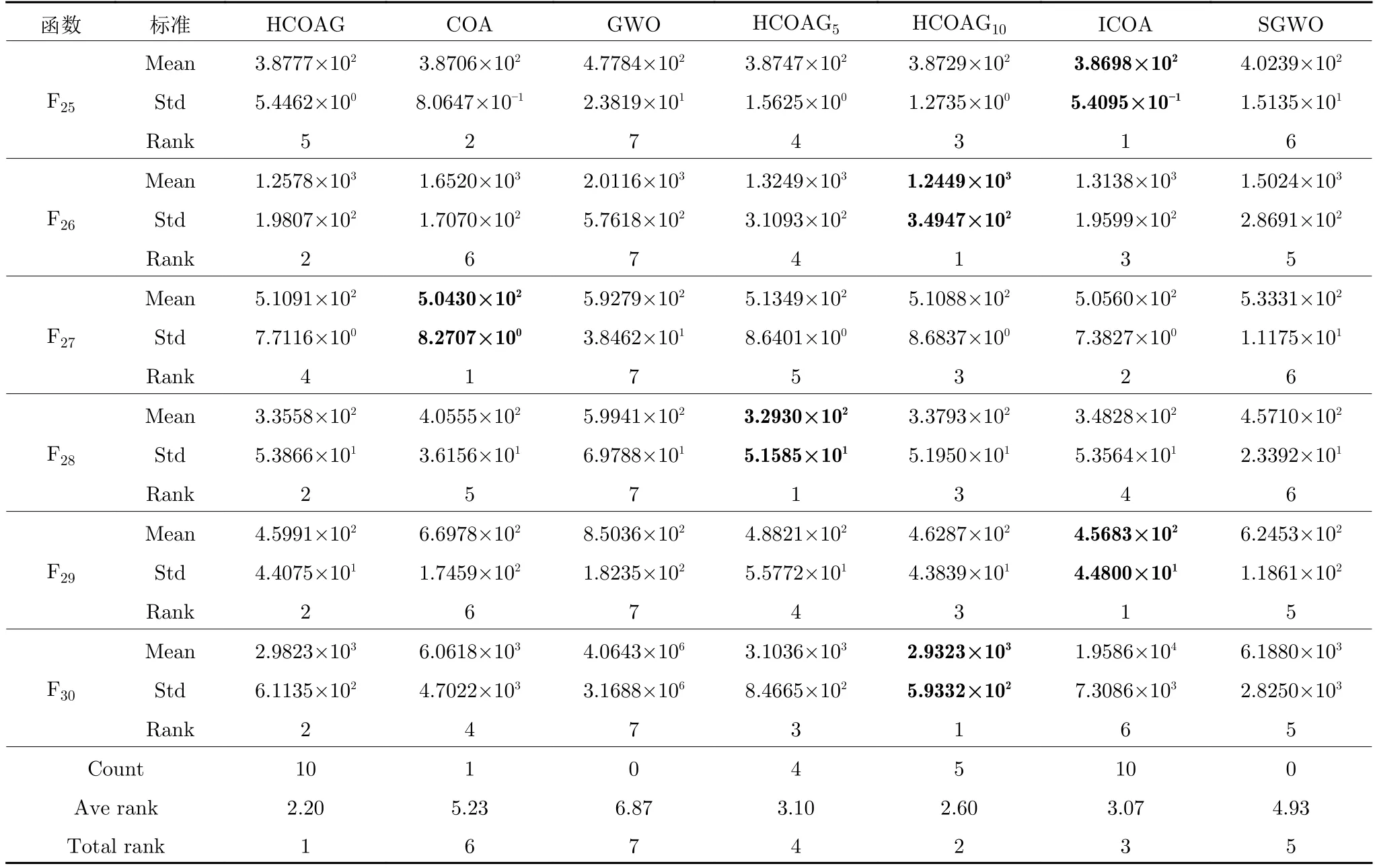
表1 HCOAG 与其不完全算法的结果对比 (续表)Table 1 Comparison results of HCOAG and its incomplete algorithms (continued table)
4.3 在经典函数上的优化性能对比
为验证HCOAG的性能,首先将其用于经典函数的优化实验,并将其结果与COA、GWO、HFPSO和DEBBO的结果进行对比,实验结果见表2.
为了能说明问题,选择6 个经典的、具有代表性的基准函数的实验结果作为示例进行分析和讨论,这6 个函数的信息如表3 所示,其中f1~f3和f4~f6分别作为单峰函数和多峰函数的代表.在此实验中,由于HCOAG 是COA 和GWO的混合算法,故选择COA 和GWO 作为对比算法.HFPSO和DEBBO 是目前两种较为优秀的混合算法,故选为HCOAG的对比算法.
从表2 可以看出,在D=10和D=30 上,COA无论是在单峰还是在多峰函数上优化性能最差,说明COA 在处理这些经典函数优化问题上无优势.在单峰函数的均值和方差上,除了f3外,GWO 均优于HCOAG 以及其他3 种对比算法,证明了GWO具有较好的开采能力.在多峰函数上,HCOAG的性能最佳,说明GWO 与全局搜索能力强的COA混合有效.

表2 在6 个经典函数上的实验结果对比Table 2 Comparison results on the 6 classic functions

表3 6 个经典函数的情况Table 3 Details of 6 classical benchmark functions
从整体上看,在D=10和D=30 上,HCO-AG的总体平均排名为1.33,其他算法的平均排名依次为:HFPSO (2.50)、GWO (2.75)、DEBBO(2.92)和COA (5.00).这些结果表明,HCOAG 不是对所有优化问题都有绝对优势,在单峰函数上优化性能稍差.而GWO 在单峰函数上具有优势,对HCOAG的性能具有一定的贡献.从整体上看,HCOAG 在经典函数上具有较好的优化性能.
为直观显示HCOAG、COA、GWO、HFPSO和DEBBO的收敛性能,给出了这5 个算法的收敛图.限于篇幅,本节在D=30 上选取2 个单峰函数(f1和f2)和2 个多峰函数(f5和f6),如图5 所示.在单峰函数上,与HCOAG、COA、HFPSO 和DEBBO算法相比,GWO 收敛速度更快,表现出更好的收敛性能.在多峰函数上,与COA、GWO、HFPSO和DEBBO 算法相比,HCOAG 表现出了更好的收敛性能.综上所述,表2 和图5 说明了GWO 具有较好的局部搜索能力和收敛性能,也部分证明了利用GWO 局部搜索能力强的优势对COA的混合改进是必要和可行的.

图5 HCOAG 与对比算法在4 个经典函数上的收敛图Fig.5 Convergence curves of HCOAG and the comparison algorithms on the 4 classical benchmark functions
4.4 在CEC2017 复杂函数上的优化性能对比
为了进一步验证HCOAG的搜索能力,将其用在CEC2017 复杂函数上实验,并将其结果与9 个代表性的先进算法COA、GWO、MEGWO、HFPSO、DEBBO、SaDE、SE04、FWA 和TLBO的实验结果进行比较,其结果见表4,其中SaDE和SE04的实验数据直接来自文献[20].
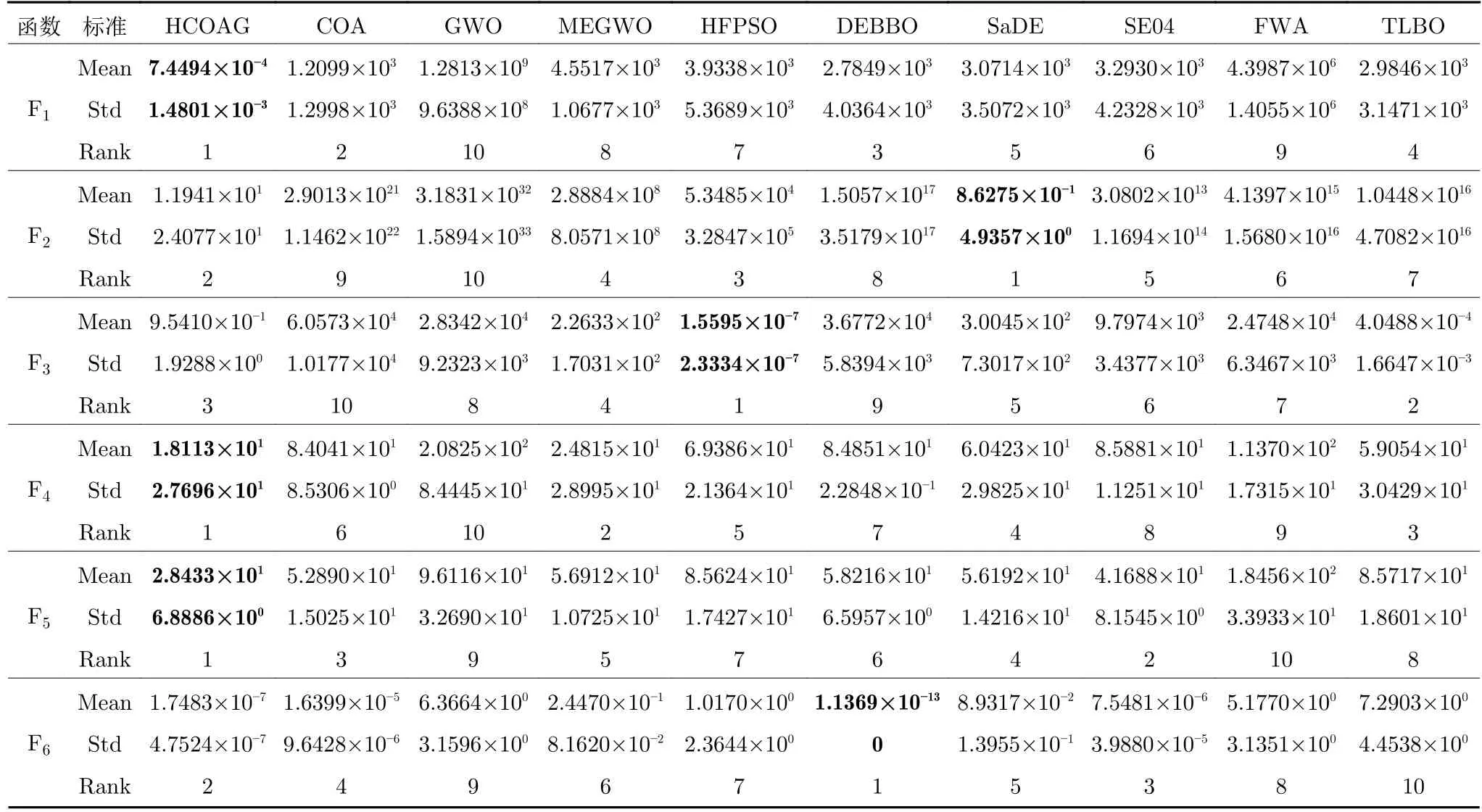
表4 在30 维CEC2017 复杂函数上的优化结果对比Table 4 Comparison results on the 30-dimensional complex functions from CEC2017
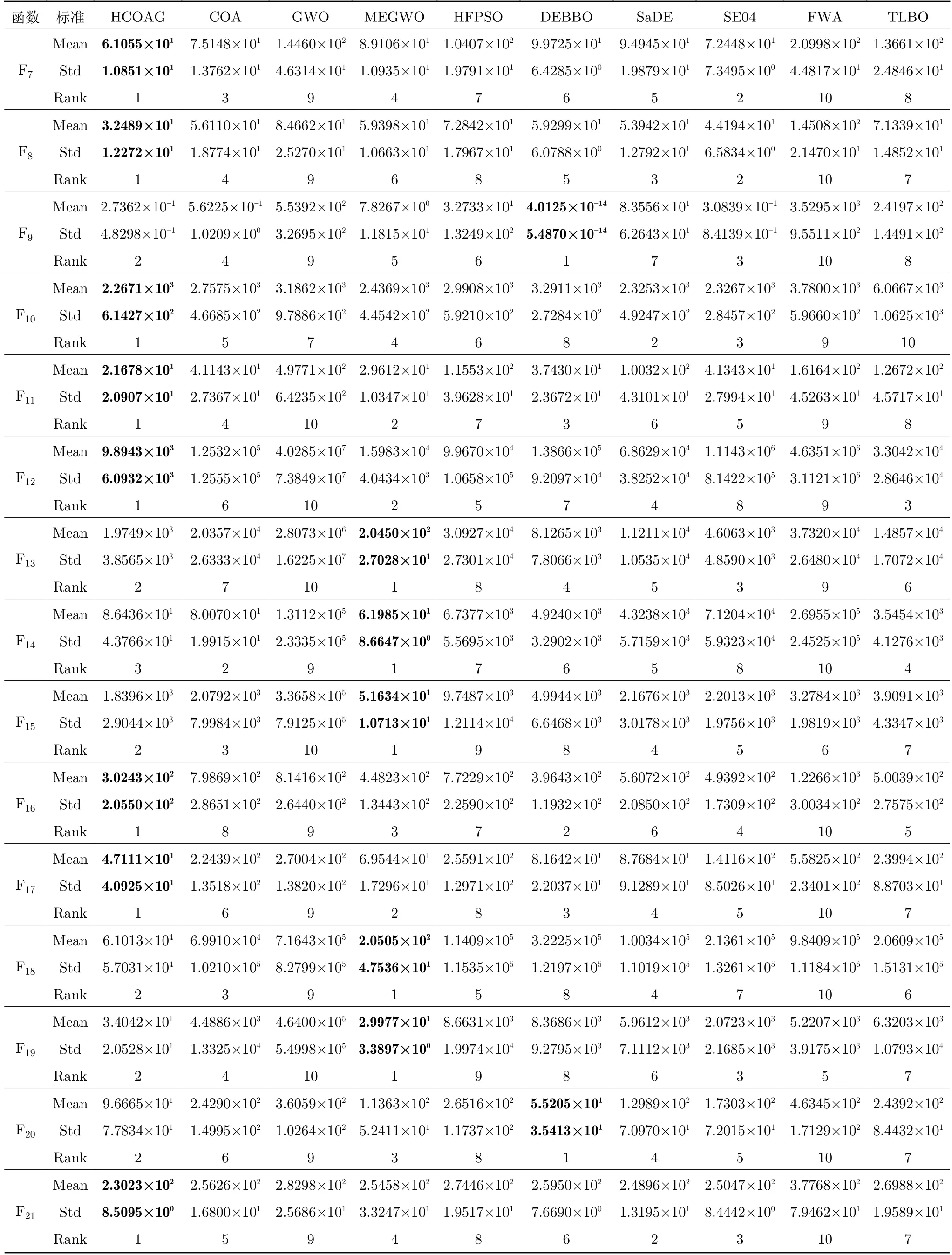
表4 在30 维CEC2017 复杂函数上的优化结果对比 (续表)Table 4 Comparison results on the 30-dimensional complex functions from CEC2017 (continued table)

表4 在30 维CEC2017 复杂函数上的优化结果对比 (续表)Table 4 Comparison results on the 30-dimensional complex functions from CEC2017 (continued table)
在均值和方差上,与MEGWO 相比,HCOAG 优于23 次.与同为混合算法的HFPSO 和DEBBO 相比,HCOAG 分别优于29 次和23 次.与SaDE 和SE04 相比,HCOAG 分别优于28 次和29 次.与FWA 和TLBO 相比,HCOAG 分别优于30 次和29 次.在总排名上,HCOAG 排名第一,接下来依次为MEGWO、DEBBO、SaDE、SE04、COA、TLBO、HFPSO、FWA、GWO.因此,HCOAG的性能优于9 个先进对比算法的性能.
4.5 收敛性能分析
为了验证HCOAG的收敛性能,给出HCOAG与COA、MEGWO、DEBBO、TLBO 和HFPSO在CEC2017 测试集中30 维函数的收敛图.受篇幅所限,本文仅选取有代表性的函数作为示例进行对比分析.在F1~F3中选取1 个单峰函数,即F1,在F4~F10中选取F5,F7,F8这3 个多峰函数,在F11~F20中选取F11,F12,F16,F17这4 个混合函数,在F21~F30中选取F21,F23,F24,F29这4 个复合函数,其收敛图见图6.
从图6 中可以看出,在3 个函数F1,F5和F8上,随着函数评价次数的增加,在收敛速度上,HCOAG 较对比算法要快得多,优势明显.在其余9 个函数上,虽然HCOAG的收敛速度优势不是很明显,但在收敛性能上也优于其他对比算法.总之,无论在单峰函数和多峰函数上,还是在混合函数和复合函数上,HCOAG的收敛速度都比其他对比算法的收敛速度快,表明HCOAG 具有更优秀的收敛性能.这些都说明,本文提出的高斯全局趋优成长算子、动态调整组内郊狼数方案以及简化操作的GWO 搜索算子等的采用都为收敛速度的提升做出了贡献,这些策略的融合使用是有效可行的.
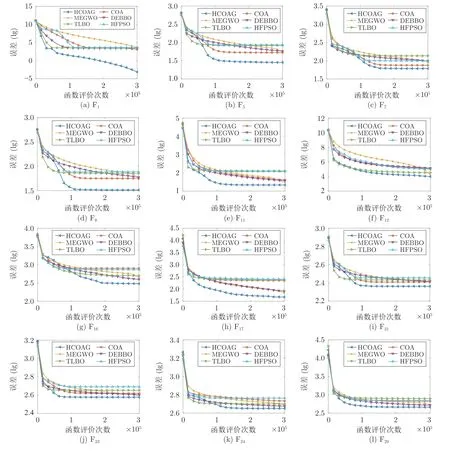
图6 HCOAG、COA、MEGWO、DEBBO、TLBO 和HFPSO的收敛图Fig.6 Convergence curves of HCOAG,COA,MEGWO,DEBBO,TLBO,and HFPSO
4.6 时间对比分析
为了考察HCOAG的运行时间,直接采用第4.4 节的实验.因为HCOAG 是COA 和GWO的混合算法,故仅记录HCOAG、COA 和GWO 在30 维CEC2017 函数上的耗时,它们在独立运行30次获得不同函数类型的平均耗时结果见图7.横坐标为不同的函数类型,纵坐标为平均时间(s).
从图7 可以看出,在单峰函数上,HCOAG 耗时(2.4443 s)是COA 耗时(2.9988 s)的81.51%,GWO 耗时(2.4222 s)是HCOAG 耗时(2.4443 s)的99.10%;在多峰函数上,HCOAG 耗时(2.9211 s)分别是COA(3.5503 s)和GWO(2.9233 s)耗时的84.25%和99.92%;在混合函数上,HCOAG 耗时(3.6246 s)是COA 耗时(4.2034 s)的86.23%,GWO 耗时(3.4981 s)是HCOAG 耗时(3.6246 s)的96.51%;在复合函数上,HCOAG 耗时(6.1480 s)是COA 耗时(7.0897 s)的86.72%,GWO 耗时(6.0822 s)是HCOAG 耗时(6.1480 s)的98.93%.故无论是单峰函数和多峰函数,还是混合函数和复合函数,HCOAG的耗时都与GWO 耗时大致持平.其主要原因是:1)HCOAG 与GWO 都采用并行计算模式,但GWO 结构简单,而其产生新解的计算复杂度(见式(12))较高;2)HCOAG 虽然采用精简GWO,但需要分组并在组内寻优,结构复杂,故二者耗时大致持平(HCOAG 耗时稍多于GWO的耗时).在耗时上,HCOAG 较COA 少,主要原因是:1)在成长过程的目标函数评价上,后者采用串行计算,前者采用并行计算减少了运行时间;2)虽然在成长过程中嵌入了GWO 搜索,但采用精简的GWO 搜索方式并未增加多少计算成本;3)前者没有郊狼被驱离和接纳操作,节省了运行时间;4)动态调整方案减少了生与死操作次数.
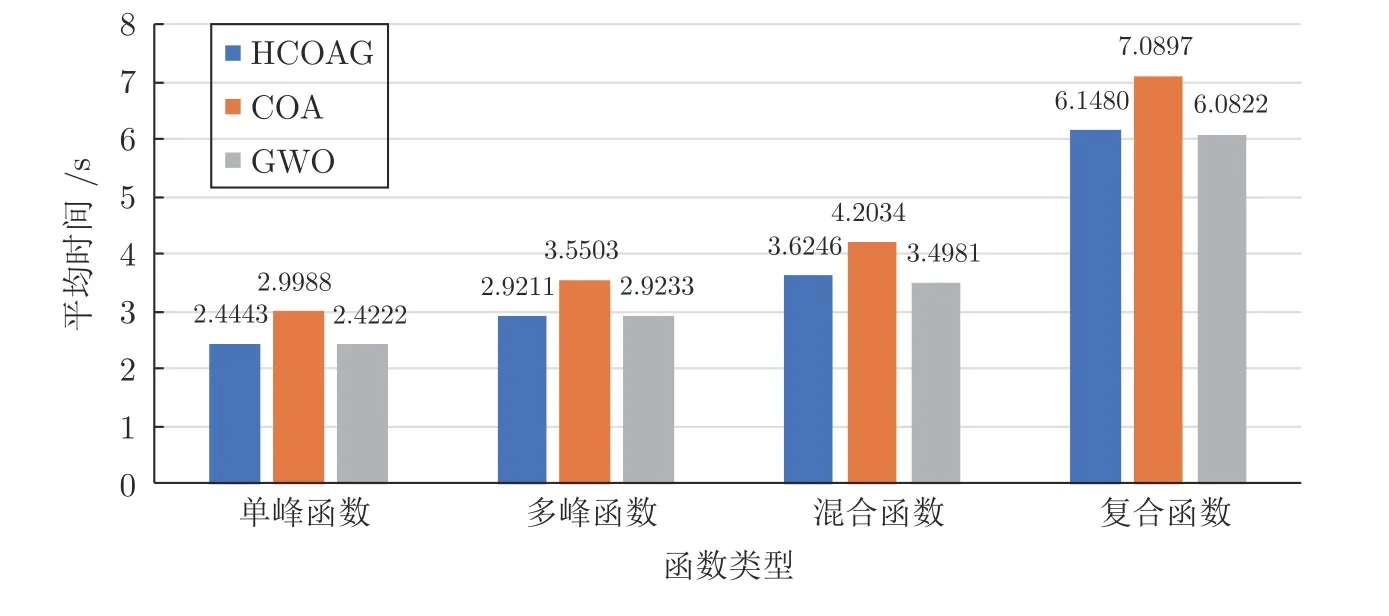
图7 HCOAG 与COA、GWO 在不同类别函数上的平均时间对比图Fig.7 Comparison bars of average time of HCOAG,COA,and GWO on different kinds of functions
综合第4.3~4.6 节,HCOAG 在较短的时间内能获得最好的优化性能,说明了其优化效率高.
4.7 上下界分析
为了能够更充分地评价HCOAG的性能,本节对其进行上下界分析,即在一个优化问题上,独立运行一定次数后考察其最坏结果和最优结果.
因为本文将HCOAG 应用于CEC2017 复杂函数集上,此函数集有30 个不同的优化问题,其全局最优解对应的最优值不同,故其获得的上下界也不同.限于篇幅,在CEC2017 四类函数上分别选取了同样的一个函数(F1,F5,F11,F29)进行上下界讨论,即在51 次的运行结果中选择最好值和最差值分别作为本文提出算法在该函数上的上下界,并与对比算法中结果最好的算法(在F1和F5上选用COA;在F11和F29上选用DEBBO)获得的上下界进行对比.
为了直观和方便对比,对3 个算法获得的结果进行了统一的处理:即将每个算法每次独立运行结果减去理想的最优函数值作为最终结果,让每个函数的理想最优值为0.在4 个函数上的上下界结果见表5.
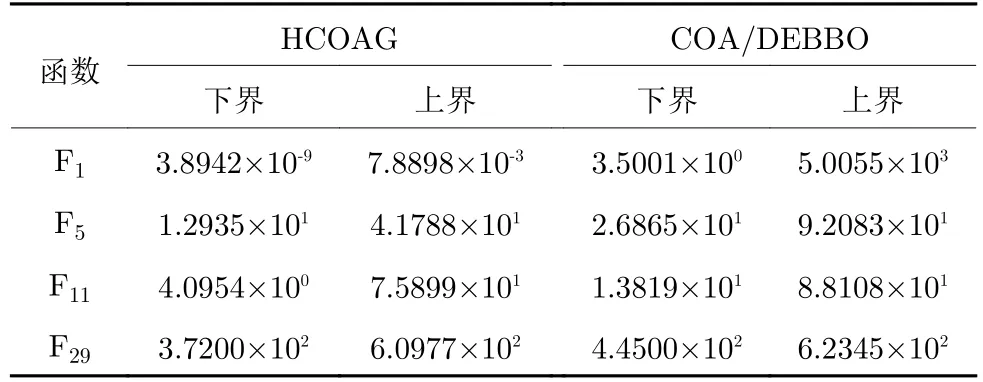
表5 在30 维CEC2017 复杂函数上的上下界结果对比Table 5 Comparison of upper and lower bounds on the 30-dimensional complex functions from CEC2017
从表5 可以看出,在4 个函数上,无论上界还是下界,HCOAG 都比对比算法小,说明本文提出的算法比对比算法好,也证明了本文提出算法的有效性.
4.8 渐进收敛性分析
依据文献[23]的随机泛函分析方法原理,本节对HCOAG的收敛性进行分析.从算法3的描述和HCOAG 流程图(图4)可以看出,HCOAG 由3个算子完成新解的产生,即高斯全局趋优成长算子、简化GWO 搜索算子以及生与死算子.高斯全局趋优成长算子类似DE (Differential evolution)中的DE/rand-to-best/1/bin 变异算子;简化GWO 搜索算子类似DE 中的DE/best/1/bin 变异算子;生与死算子相当于遗传算法中的变异算子.3 个算子产生的新解都采用贪心算法严格基于优胜劣汰策略,通过淘汰新解与原解中较差者产生更优的新一代个体.故对于最小优化问题,HCOAG 评价函数序列为单调非递增序列.为了证明HCOAG的渐近收敛性,首先做如下定义.
定义1.设Q(t)表示X(t)的中间群体,Vc,j(t+1)∈Q(t+1),则HCOAG 搜索算子定义如下:
高斯全局趋优成长与简化GWO 搜索混合算子定义为
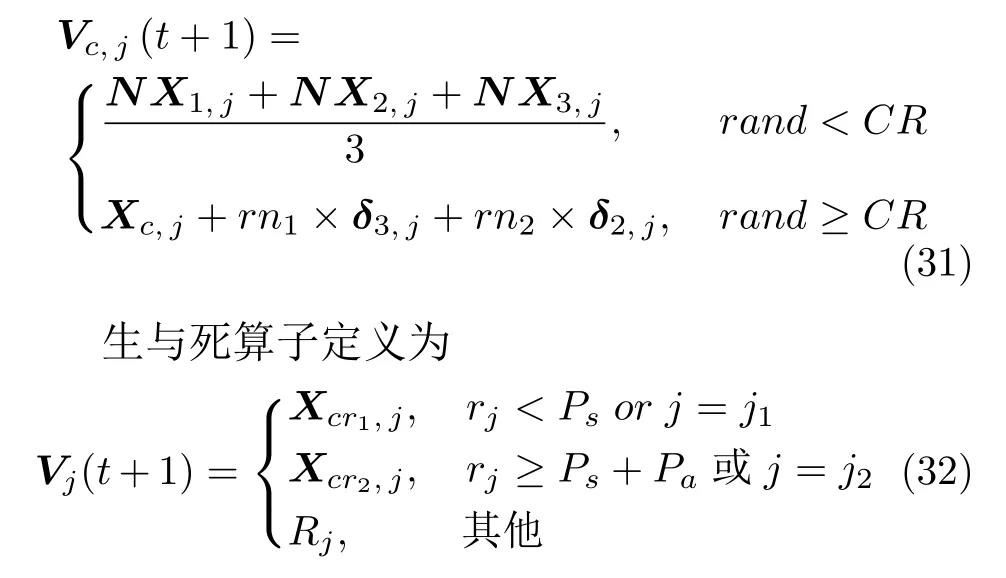
假设f(X)为 最小优化函数,解空间S=X|X={x1,x2,···,xD}且Lj ≤xj ≤Uj,j=1,2,···,D}为D维欧氏空间 RD的有界子空间.为了在进行数值计算时不受计算精度的限制,设定HCOAG的计算精度保留到小数点后第k位数字.
定义2.两种算子的混合策略是一种按照概率CR/D和(1-CR/D)对群体中个体向量的每一维分量分别采用简化GWO 搜索算子和高斯全局趋优成长算子以及在每一组中最差郊狼上采用生与死算子进行重组变换的过程,它是解空间上的一种随机映射ψ:Ω×S→S2,可定义为

定理1.HCOAG的一次迭代所形成的随机映射ψ′是一个随机压缩算子.
再依据文献[23]引理2,即可得到HCOAG 渐进收敛的结论,即定理2.
定理2.设ψ′为HCOAG 形成的随机压缩算子,则ψ′具有唯一的随机不动点,即HCOAG 是渐进收敛的.
4.9 Wilcoxon 符号秩检验和Friedman 检验
Wilcoxon 符号秩检验方法[24]是一种非参数统计性检验方法,目的在于检验两个样本均值之间的显著差异.其中p值由R+和R-计算可得,R+表示正秩总和,R-表示负秩总和,具体见式(34)和式(35),di为两种算法在n个问题中第i个问题上的性能分数的差值.当HCOAG 算法与对比算法性能相同时,对应的秩平分给R+和R-.为检验HCOAG 与表4 中对比算法的显著性差异,在软件IBM SPSS Statistics 24 上实现Wilcoxon 检验,结果如表6 所示.表6 中,n/w/t/l表示在n个函数上HCOAG分别优于对比算法w次,与对比算法相等t次,劣于对比算法l次.
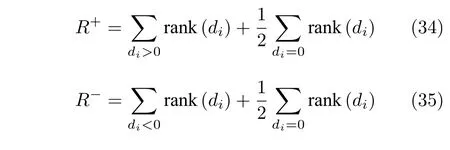
从表6 可以看出,与COA 和GWO 相比,p值分别为1.3039×10-7和1.8626×10-9,均小于0.05,表明HCOAG 显著优于COA 和GWO,再一次说明COA 和GWO 二者的改进与混合是有效的.HCOAG 与MEGWO、HFPSO、DEBBO、SaDE、SE04、FWA 和TLBO 相比的p值均小于0.05,表明HCOAG 也显著优于这些对比算法.

表6 Wilcoxon 符号秩检验结果Table 6 Wilcoxon sign rank test results
Friedman 检验是一种非参数双向方差分析方法[24],目的在于检测两个或多个观测数据之间的显著性差异.具体实现过程分为3 步:1)收集每个算法或者问题的观测结果;2)对于每个问题i的从1(最好结果)到k(最差结果)的排名值,定义为(1 ≤j≤k);3)在所有问题中求出每个算法的平均排名,得到最后排名在零假设下所有算法的行为相似(它们的秩Rj相等),Friedman统计值Ff的计算方式如式(36),当n和k足够大时(根据经验n> 10,k> 5),它是按照k-1 自由度的x2分布的.为了再次验证HCOAG的显著性,依据表4 对HCOAG 和对比算法在软件IBMSPSS Statistics 24 上实现Friedman 检验,其结果如表7 所示.
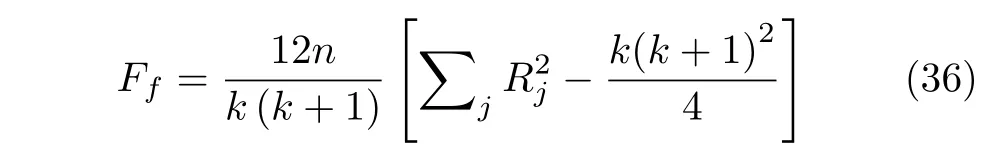
从表7 可以看出,在30 维复杂函数上,通过Friedman 检验获得的渐进显著性p值为6.3128×10-31,由于得到的渐进显著性小于0.01,所以在30维上HCOAG 与对比算法之间存在显著性的差异.HCOAG 算法的秩均值(1.73)最小,随后依次是MEGWO、DEBBO、SaDE、SE04、COA、TLBO、HFPSO、FWA 和GWO,表明HCOAG的优化性能最好.结合Wilcoxon 符号秩检验和Friedman 检验结果可以得出,HCOAG 总体上明显优于先进的对比算法.

表7 Friedman 检验结果Table 7 Friedman test results
5 HCOAG 在K-Means 聚类优化上的应用
聚类在数据挖掘领域发挥着十分重要的作用,通过对聚类的数据分析可以得到数据的具体分布情况以及掌握数据类型的特点[25].其中,最常用的聚类方法是K-Means 方法[26],其在n个样本数据中的具体实现过程如下:首先随机产生K个初始聚类中心,然后计算每个样本与各聚类中心的距离,接着将样本与距离最近的聚类中心划分到一个组内,形成K个组,最后重新计算每个组内所有样本的均值作为新聚类中心并进行下一次划分,如此迭代执行划分过程直到满足终止条件为止.K-Means 方法具有原理简单、可伸缩性好以及效率高等优势,但存在对初始点敏感和易陷于局部最优等问题.目前已有研究将SIOA 运用到K-Means 聚类中,很好地解决了K-Means 算法存在的一些问题[25,27].本节采用HCOAG 优化K-Means 聚类以解决其对初始点敏感等问题,其中,目标函数的定义为

其中,E是数据集中所有数据点到所属聚类的聚类中心的距离和,K是聚类中心个数,ck是第k个聚类中心位置,Ck是第k个聚类簇,xi是聚类族Ck中第i个数据点.将HCOAG 应用到K-Means上,首先假设每头郊狼由k个聚类中心组成,则解向量的维数应等于k× 数据样本的特征数,目标函数采用式(37);接着执行HCOAG,直到满足算法的终止条件,输出最优聚类中心.
实验采用UCI 数据库(http://archive.ics.uci.edu/ml/datasets.php)中7 个标准数据集(见表8 第1 列)来验证HCOAG 在K-Means 聚类优化上的有效性,数据集名称后的括号内的数字为样本数、属性数和聚类数.选取的5 个对比算法包括:COA、MEGWO、HFPSO、擅长聚类优化的改进的粒子群优化算法(Improved PSO,IPSO)和改进的遗传算法(Improved genetic algorithm,IGA).其中,IPSO 和IGA 来自“http://yarpizcom/64/ypml101-evolutionary-clustering”.所有算法的公共参数设置相同:N=50,MaxDT=200,Num=30.表8是6 种算法独立运行30 次获得的均值、方差和排名结果.
从表8 可知,HCOAG 在7 个数据集上的均值和方差得到排名第一5 次,其次是HFPSO 和IPSO 均为1 次,COA、MEGWO 和IGA 均获得0次第一.HCOAG的平均排名为1.43,其他算法的平均排名顺序依次为:IPSO、IGA、MEGWO、HFPSO 和COA.以上结果都表明HCOAG 在KMeans 聚类上的优化性能最好.总之,HCOAG 在K-Means 聚类优化中获得竞争性的优化性能,能够更好地处理聚类优化问题.

表8 6 种算法在K-Means 聚类优化上的结果对比Table 8 Comparison results of the 6 algorithms on K-Means clustering optimization
6 结束语
针对COA 存在的不足,本文提出了一种COA与GWO的混合算法(HCOAG).首先,改进COA(ICOA).1)在成长过程中,提出一种高斯全局趋优成长算子,提高了搜索能力;2)提出一种动态调整组数方案,搜索前期采用较少组数,减弱全局最优解的正反馈作用,强化探索能力,后期采用较多组数,增强全局最优解的正反馈作用,强化开采能力,并提高可操作性.然后,对GWO 进行改进,提出了一种精简的GWO (SGWO),在发挥其局部搜索能力强的优势同时,提高了可操作性.最后,采用正弦交叉策略将ICOA 与SGWO 有机融合,很好地平衡了组内郊狼的探索与开采能力,从而获得了最佳优化性能.大量经典函数与CEC2017复杂函数优化的实验结果表明,在经典函数上,COA不及GWO;在复杂函数上,GWO 不及COA;而HCOAG 在两类优化问题上都有更好的性能,说明二者混合有必要和有效;与其他先进的对比算法相比,HCOAG具有更好的优化性能.K-Means 聚类优化结果表明,与对比算法相比,HCOAG 获得了竞争性的优化性能.
总之,与COA 相比,HCOAG 具有如下优势:1)普适性强,经典函数和复杂函数优化以及聚类优化3 组实验结果表明,HCOAG 都有更好的表现;2)耗时少,因此有更好的搜索效率;3)更好的收敛质量;4)更强的稳定性和鲁棒性,5)可操作性更强.
COA 是最近提出的一种SIOA,尚有许多地方需要探讨和完善,本文仅是一种混合改进研究的尝试.未来将进一步改进COA,对其进行深入的理论研究,并拓展其应用领域.

