淮南深地重力观测的环境噪声评估与慢地震探测潜力

王振宇，王赟，徐如刚，刘泰，付广裕*，孙和平

1 中国地震局地震预测研究所，北京 100036 2 中国地质大学（北京）地球物理与信息技术学院，北京 100083 3 安徽省地震局，合肥 230031 4 中国科学院精密测量科学与科技创新研究院大地测量与地球动力学国家重点实验室，武汉 430077

0 引言

早在20世纪50年代，美国等发达国家就开始利用废旧矿井和山体中的隧道空间建设地下实验室，并主要开展基础物理、高能粒子与暗物质等天体物理和宇宙学研究，兼有部分地球科学、力学、生物医学等学科的探索（贺永胜等,2018）.截至目前仍在运行的以美国的Soudan和DUSEL、意大利的Gran Sasso、加拿大的SNO、日本的Kamioka、韩国的Y2L、法国的Modane和LSBB、英国的Boulby、西班牙的Canfranc、俄罗斯的Baksan、比利时的Membach、卢森堡的Walferdange等地下实验室最为著名，其在引力波、中微子、暗物质、超纯材料制造、高精度检测装备技术等方面取得了突出的成果.

地下实验室对于地球物理观测具有非常积极的意义.重力观测是了解地球动力学过程的重要地球物理方法之一，扣除了潮汐、极移、气压等已知信号的重力残差蕴含地球内部活动的重要信息.重力残差受仪器自身漂移、热噪声和环境噪声影响，地下实验室为降低外部环境影响提供了理想的观测条件：Rosat和Hinderer（2018）对法国LSBB低噪声地下实验室的超导重力仪观测数据进行了分析，认为其地震噪声水平与目前公认的最安静重力观测站（德国BFO测站，Rosat and Hinderer,2011）相当，LSBB测站与BFO测站的次地震频段功率谱密度也十分接近；Francis（2021）在卢森堡的WULG实验室对CG-5型弹簧重力仪和CG-6型弹簧重力仪进行了性能测试，发现二者的长期漂移分别低至63.27×10-9m·s-2/h和-13.79×10-9m·s-2/h，明显低于地表观测的结果.此外，地下重力观测还对深部结构十分敏感：Tanaka等（2013）将一台gPhone型重力仪在日本的瑞浪地下实验室和地表分别观测一段时间，他们发现将地下与地表记录叠加可以有效地消除降水的影响，且放大来源于深部的信号；Tanaka和Honda（2018）利用瑞浪实验室的3台重力仪组成的垂向台阵，进一步研究了地下水位和深部结构对重力的影响.综上所述，地下实验室重力观测相比于地表观测具有低环境噪声和探测深部信号方面的优势.

淮南深地实验室是我国首先开展地下多物理场观测实验研究的地下实验室，深达地下871 m，由潘一东矿井下巷道改建而成.该深地实验室地处华北块体南部，东邻郯庐断裂带次级断裂张八岭断裂的固镇—怀远段，南抵大别山余脉八公山（图1），紧邻苏鲁—大别超高压变质带，适于探索华北块体与华南块体之间的相互作用，以及揭示太平洋板块向西俯冲远场效应的重力观测与研究.淮南深地实验室具有4个大口径直立竖井和2个深达地下-848 m和-1042 m的水平巷道，为各种高精度观测提供了良好的观测条件.张苗苗等（2021）在此实验室进行过先期重力观测，其噪声分析结果表明地下噪声水平显著低于地表，可为高精度重力观测提供超静的环境支持.

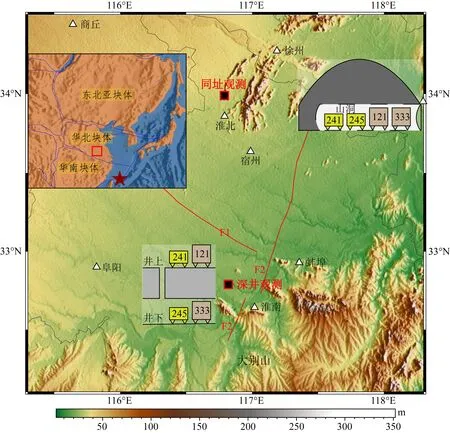
图1 重力观测点位置图图中红色实线表示断裂，F1：涡河断裂，F2：郯庐断裂带固镇—怀远段；仪器241和245为CG-6型重力仪，仪器121和333为CG-5型重力仪；左侧子图红框表示研究区域在东亚地区的位置，蓝线为主要块体边界，五角星表示冲绳海沟地震位置.Fig.1 Location map of the gravity observation stationRed lines denote faults,F1:Wohe fault,F2:Guzhen-Huaiyuan segment of Tanlu fault zone.No.241 and No.245 are CG-6 gravimeters.No.121 and No.333 are CG-5 gravimeters.The subfigure on the left side shows the position of the study area in East Asia.Blue lines denote main block boundaries and red star denotes Okinawa Trench earthquake.

本研究利用淮南深地实验室地下-848 m巷道，联合地表观测建立立体式重力观测台阵，开展静态连续重力对比观测；结合山洞内部静态漂移观测实验结果，进行潮汐分析并对比噪声水平的差异，再次探索深地环境对于高精度重力观测的重要价值.

1 数据与预处理

本研究的数据采集由4台相对重力仪分两期完成.4台仪器包括2台CG-5型弹簧重力仪（编号分别为121和333）和2台CG-6型弹簧重力仪（编号分别为241和245），仪器部分主要参数见表1.一期观测为4台仪器的同址观测，观测时间为2020年12月29日至2021年1月7日，观测地址为中国大陆构造环境监测网络淮北连续重力站（简称淮北重力站）山洞内（图1），观测目的是对4台重力仪的观测性能进行初略评估.重力观测室距离洞口60 m，设置有4套密封船舱门，洞内温度恒定为15.5 ℃，日温差小于0.05 ℃，年温差小于0.1 ℃.二期观测为淮南深地实验室地表与井下巷道同步观测，观测时间为2021年4月14日至2021年4月23日；地表观测由CG-5型121号和CG-6型241号重力仪完成，井下巷道观测由CG-5型333号和CG-6型245号重力仪完成.两期观测的采样率均为1 min.

表1 不同仪器性能参数Table 1 Parameters of CG-5 gravimeter and CG-6 gravimeter

为了去除原始观测数据中包含的电压突变和地震等干扰，本研究利用Tsoft软件对原始数据进行预处理（Van Camp and Vauterin,2005）.去除干扰后对观测信号进行一次函数拟合以去除长期线性漂移，线性漂移改正的结果如图2和图3所示.不同型号仪器间的线性漂移有显著的差异，CG-6型重力仪的观测信号中有清晰的周期性潮汐信号，而在CG-5型重力仪的结果中此类信号被较大的线性漂移所掩盖.在淮北重力站实验中，CG-5型121号、333号和CG-6型241号、245号重力仪的漂移分别为0.7847 mGal·d-1、0.7080 mGal·d-1、-0.0233 mGal·d-1和-0.0219 mGal·d-1，可见CG-6型重力仪的线性漂移比CG-5型重力仪小一个数量级，而同类型仪器的漂移率基本一致.

在淮南深地实验中，CG-5型121号、333号和CG-6型241号、245号重力仪的漂移分别为0.6502 mGal·d-1、0.4701 mGal·d-1、-0.0184 mGal·d-1和-0.0080 mGal·d-1.与淮北重力站的线性漂移改正结果类似，淮南深地实验的结果也表明不同类型仪器的性能差异显著.值得注意的是即便仪器型号相同，井下深部地下巷道2台仪器的漂移也要小于地表的2台仪器，减小量达到1/3至1/2.鉴于淮北重力站的同址观测中同类型仪器表现出了接近的漂移结果，这种漂移的减小可以归结为井下巷道低噪声环境导致的.Francis（2021）的WULG地下实验室研究表明：CG-5型008号重力仪的漂移约为0.1519 mGal·d-1，远低于本次深地实验室的观测结果，这是由于该仪器长期安置于地下实验室，而本次观测所用的2台CG-5型仪器日常多用于野外流动观测，仪器损耗程度不同；CG-6型003号重力仪的漂移约为0.0331 mGal·d-1，略大于淮南井下观测的结果，也高于淮北重力站实验中CG-6型241号的-0.0233 mGal·d-1、245号的-0.0219 mGal·d-1的漂移结果，造成此现象的原因需要后续长期观测来解释.

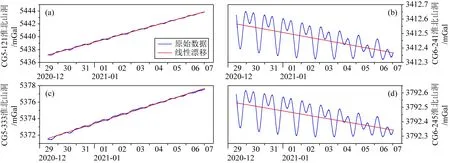
图2 淮北重力站各重力仪线性漂移改正结果（a） CG-5型121号仪器；（b） CG-6型241号仪器；（c） CG-5型333号仪器；（d） CG-6型245号仪器.图中蓝线表示原始观测数据，红线表示一次函数拟合结果.Fig.2 Linear drift correction on gravity observation at Huaibei cave（a） No.121 CG-5 gravimeter;（b） No.241 CG-6 gravimeter;（c） No.333 CG-5 gravimeter;（d） No.245 CG-6 gravimeter.Blue and red lines denote original observation and one-degree fitting,respectively.

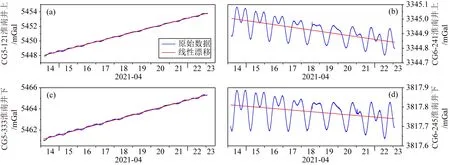
图3 淮南深地实验各重力仪线性漂移改正结果（a） CG-5型121号仪器；（b） CG-6型241号仪器；（c） CG-5型333号仪器；（d） CG-6型245号仪器.图中蓝线表示原始观测数据，红线表示一次函数拟合结果.Fig.3 Linear drift correction on gravity observation at Huainan mine（a） No.121 CG-5 gravimeter;（b） No.241 CG-6 gravimeter;（c） No.333 CG-5 gravimeter;（d） No.245 CG-6 gravimeter.Blue and red lines denote original observation and one-degree fitting,respectively.

经过线性漂移改正后，还需要扣除海潮负荷响应、气压响应、极移等效应的影响（Rosat et al.,2018;Sun et al.,2019）.本研究所用海潮模型为NAO99b（Matsumoto et al.,2000，可自http:∥holt.oso.chalmers.se/loading/网站下载），气压、极移以及非海潮水文负荷效应由法国斯特拉斯堡大学地球科学观测学院负荷服务平台（EOST/IPGS,http:∥loading.u-strasbg.fr）计算.由于山洞内和井下巷道气压影响很小，气压改正只应用于地表观测数据.预处理的线性漂移、气压响应等效应也可以通过第2节介绍的潮汐分析校正，但为了确保这些干扰被剔除，本研究仍在预处理过程中进行单独处理.

2 潮汐分析与噪声分析方法

经预处理的重力观测结果gi如图4a和图5a所示，根据Tamura等（1991），观测重力信号gi可解耦为潮汐信号ti、气压响应ri、非线性项（包含非线性漂移和趋势项）di和随机噪声（不规则项）ei，即：

gi=ti+ri+di+ei，

（1）

i表示时间序列，调和分析方法可将潮汐信号ti分解为若干个潮波信号的组合，在假设各个波群的振幅和相位恒定的条件下，ti的展开形式为：

（2）

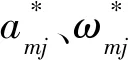
（3）

Vmj为引潮位的振幅系数，g和r分别为观测点的重力加速度和地球半径.获取潮汐因子am和相位φm等参数的过程即潮汐分析.

由公式（1）可知，准确提取各潮汐分量的前提是完整地扣除其他信号.由于已进行了气压改正，响应信号ri无需考虑；随机噪声ei通常比其他信号小1到2个数量级，可认为是扣除了其他信号的残差，因此潮汐分析的关键在于获取非线性漂移项di.如果非线性漂移像简正模一样可确定，则可以用多项式或其他简单函数的组合对其拟合并扣除（Banka and Crossley,1999）.但通常漂移包含了重力仪内部组件的随机运动，是不确定的.Ishiguro等（1998）提出使用更复杂的随机游走模型来表示漂移：

di=2di-1-di-2+ui，

（4）

其中ui为白噪声序列.于是潮汐分析的目标函数JB可写作：

（5）

v2为ABIC（Akaike′s Bayesian Information Criterion，赤池贝叶斯信息准则）非线性拟合的权重超参数（Akaike,1998）.本研究使用基于上述方法开发的BAYTAP-G软件（Tamura et al.,1991）进行潮汐分析.该软件自开发以来，在重力、应变和倾斜潮汐分析中有广泛应用（Lu and Wen,2017;Kitagawa et al.,2020;Yukutake et al.,2022）.陈晓东和孙和平（2002）与佘雅文等（2015）的研究表明，BAYTAP-G软件与Eterna软件（Wenzel,1996）具有一致的潮汐分析精度.

经潮汐分析后，需对重力残差进行功率谱密度（PSD）分析.目前主要有两种处理流程：（1）对扣除了潮汐信号的残差进行9阶多项式拟合和扣除，再对观测时段内最平静的5天数据进行功率谱密度分析（Banka and Crossley,1999）；（2）直接对潮汐信号ti、非线性项di和不规则项ei计算功率谱密度.在第一种流程中，利用9阶多项式对重力数据进行拟合和扣除可以去除仪器非线性漂移和残存的潮汐信号，目前在Tsoft等重力数据处理软件中都有实现该功能的函数，但同时也会将由物质迁移导致的重力变化信号一并扣除.李航等（2020）的研究表明扣除9阶多项式会导致残差数据中包含大量噪声能量.另外，由于本研究的观测时间较短，噪声水平随时间并无明显变化，很难筛选出最平静时段.综上，本研究采用第二种功率谱分析流程.具体计算方法为采用Welch平均功率图法（Welch,1967），窗函数选取汉宁窗，窗长为12 h，滑动步长为6 h（Berger et al.,2004;Rosat et al.,2018）.由于未进行最平静时段筛选，导致本研究的噪声水平略高于长期观测的研究（Rosat et al.,2018），但并不影响山洞、地表和井下巷道的观测结果对比.

3 结果与分析

3.1 潮汐分析

用上述方法分离的重力信号如图4和图5所示.在淮北重力站实验中，CG-5型333号仪器的观测结果具有明显的异常，其非线性项di的变化范围达到-120 μGal至60 μGal，远超过其他3台仪器的变化范围（图4c，CG-6型2台仪器均为-5 μGal至10 μGal，CG-5型121号仪器为-15 μGal至10 μGal）.非线性项di包含非线性漂移和由物质迁移导致的微小重力变化，考虑到观测时段较短，且观测期间淮南地区未发生强震，也无大规模降雨事件发生，这意味着地震活动或局部水负荷变化导致的重力变化可以忽略，因此CG-5型333号仪器记录的异常现象应该是由其自身仪器性能较差所致.更关键的是，其他3台仪器的观测数据无论是形态还是幅度均没有类似的重力变化，因此可以判定CG-5型333号仪器非线性漂移过大，对其数据gi产生影响（图4a）.4台仪器的不规则项变化幅度均小于1 μGal，说明各仪器的重力残差基本一致.尽管受到了非线性项过大的影响，但是CG-5型333号仪器记录的潮汐信号与其他仪器差别不大，即全部仪器均有较好的潮汐观测能力.

相比于淮北重力站的观测结果，淮南矿井实验的井下巷道观测数据在非线性项di方面有很大提升，CG-6型245号仪器的变化范围缩减至-5 μGal至5 μGal，而CG-5型333号仪器的变化范围缩减至-20 μGal至15 μGal，地表观测组的观测结果则没有明显变化.这说明深地井下巷道观测可以有效地降低重力观测仪器的非线性漂移量，并且对于不同类型仪器的效果存在差异.对于同类型仪器，CG-6型井下巷道地下实验室的245号仪器非线性项曲线在形态上比地表的241号更平滑，幅值也更小（减小1/3左右）.CG-5型333号仪器的情况比较特殊，其非线性漂移比山洞内减小了3/4左右.考虑到CG-5型重力仪的观测结果受弹簧松弛、倾斜和外部温度影响（Francis,2021），弹簧倾斜可以手动校正，而山洞内温度基本恒定，因此可以推断井下巷道观测主要改善了弹簧松弛效应.尽管CG-5型333号仪器在井下巷道地下实验室的表现优于在山洞的表现，但总体来说其非线性漂移依然是4台仪器中最大的.从不规则项ei和潮汐信号ti来看，淮南矿井与淮北重力站的结果类似，4台仪器的结果相差不大.图5d中，4台仪器观测的潮汐信号曲线几乎重合，这说明尽管高程上相差接近1 km，但地表和井下巷道的潮汐信号基本相同.需要注意的是，重力潮汐观测信号是观测时间与观测地点的函数，淮南和淮北的纬度不同，观测时间也不一样，因此图4d和图5d不具备可比性.

根据公式（2）提取的主要潮汐重力因子如图6和表2、3所示，对应的理论潮汐因子可以用来检验提取结果的正确性（周江存等,2009）.理论固体潮模型为DDW99模型（Dehant et al.,1999）.海潮模型与真实海潮的差异和局部横向不均匀效应会导致理论值与实测值之间的微小偏差，当理论值在实测值的误差范围内，即可认为二者符合较好.图6a所示的淮北重力站实验中除了M3因子，各仪器的其他因子均非常接近理论值.虽然各仪器的M3因子相差较大，但理论值与观测值之间的差异并未超出观测误差的范围.这说明山洞的观测环境非常理想，实测值与理论值偏差很小.图6b所示的淮南矿井实验结果表明，非同址观测的4台仪器观测结果产生了明显的差异，观测环境的变化对潮汐因子实测值产生了影响.除了M2和S2因子，其他潮汐因子的实测值均比较离散，地表的CG-6型241仪器的K1因子即便考虑误差范围也与理论值相差较大.无论是山洞实验还是深地实验，各仪器的M3因子的差别都是最明显的，尤其是两台CG-5型仪器.Francis（2021）的研究也表明即便在地下实验室，由于M3因子的幅度较小，CG-5型重力仪的观测结果并不可靠.

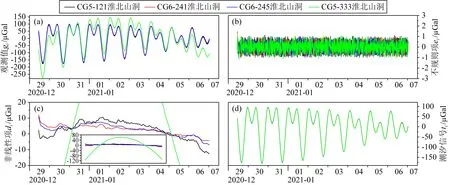
图4 淮北重力站各重力仪数据潮汐分析结果（a） 扣除线性漂移、海潮、气压、极移信号的重力观测值gi；（b） 不规则项ei；（c） 非线性项di，子图展示CG-5型333号重力仪完整结果；（d） 潮汐信号ti.黑线、红线、蓝线和绿线分别表示CG-5型121号、CG-6型241号、CG-6型245号和CG-5型333号仪器的结果.Fig.4 Tidal analysis of gravity observation at Huaibei cave（a） Gravity observation gi with linear drift,ocean tide,atmospheric pressure,and polar motion effects removed;（b） Irregular term ei;（c） Non-linear term di,the subfigure shows the complete range of No.333 CG-5 gravimeter;（d） Tidal signal ti.Black,red, blue,and green lines denote No.121 CG-5,No.241 CG-6,No.245 CG-6,and No.333 CG-5 gravimeters,respectively.

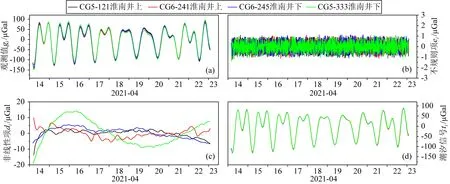
图5 淮南深地实验室各重力仪数据潮汐分析结果（a） 扣除线性漂移、海潮、气压、极移信号的重力观测值gi；（b） 不规则项ei；（c） 非线性项di；（d） 潮汐信号ti.黑线、红线、蓝线和绿线分别表示CG-5型121号、CG-6型241号、CG-6型245号和CG-5型333号仪器的结果.Fig.5 Tidal analysis of gravity observation at Huainan mine（a） Gravity observation gi with linear drift,ocean tide,atmospheric pressure,and polar motion effects removed;（b） Irregular term ei;（c） Non-linear term di;（d） Tidal signal ti.Black,red,blue,and green lines denote No.121 CG-5,No.241 CG-6,No.245 CG-6,and No.333 CG-5 gravimeters,respectively.

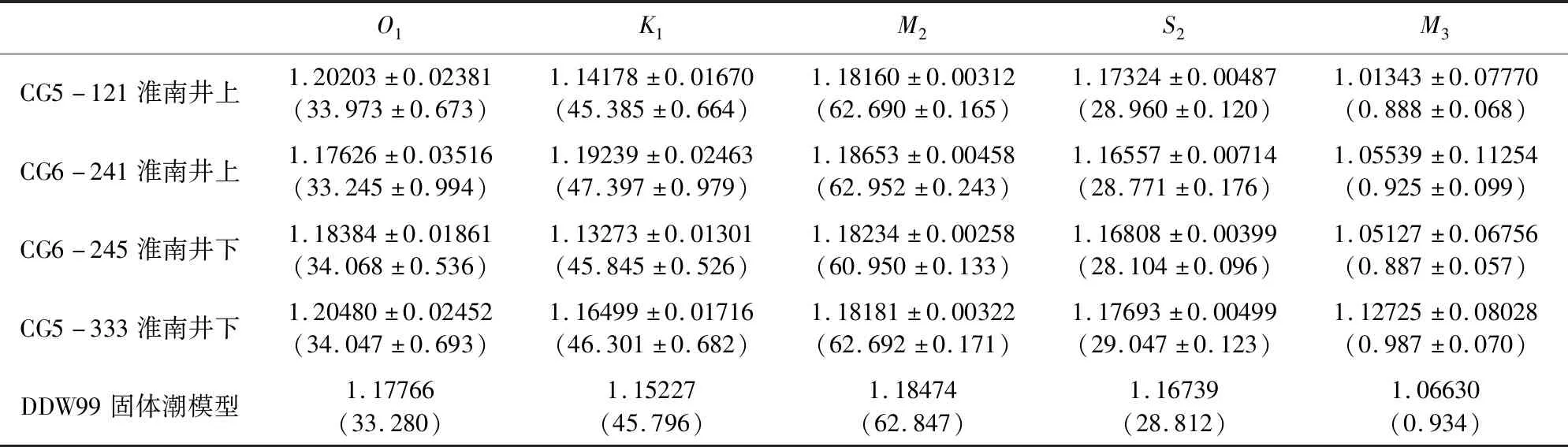
表3 淮南矿井潮汐重力因子观测结果Table 3 Observed tidal gravimetric factor results at Huainan mine

此外，潮汐重力因子的结果表明井下巷道观测的精度更高.以振幅最大、信噪比最高的M2潮波为例（Wang et al.,2021），在淮北重力站实验中，CG-6型241号和245号的M2因子观测精度分别为0.00294和0.00293（图6a子图），二者非常接近，说明在相同的观测环境下这两台仪器的观测性能是一致的.而在淮南矿井实验中，地表的241号和井下巷道深地实验室的245号仪器的观测精度分别为0.00458和0.00258（图6b子图），地表观测的精度明显低于井下巷道深地观测.潮汐信号是重力变化信号最主要的组成部分之一，通常来讲，重力仪记录的重力信号越稳定，提取的潮汐因子精度越高，因此潮汐因子的精度可视为重力观测信号质量的评判标准之一（Francis,2021）.本研究的潮汐因子精度结果说明深地实验室观测条件最好，地表观测条件最差，山洞的观测条件介于地表观测和深地观测之间.高精度潮汐因子的成功探测对于正确认识区域地壳精细结构与地幔黏滞特性均具有重要的意义.

3.2 功率谱密度

功率谱密度是表征噪声水平的有效手段，被广泛应用于仪器性能检测（Banka and Crossley,1999）.通常将1 h周期作为频段分界，小于此周期至2 min周期称为地震频段或简正模频段，大于此周期至24 h周期称为次地震频段（Rosat and Hinderer,2011）.潮汐信号主要集中在10-5Hz至10-4Hz的频段.为了评估仪器的观测能力和实验场地的噪声水平，Peterson（1993）提出了低噪声模型（Normal Low Noise Model,NLNM）表征全球最先进的地震仪在最安静环境观测的噪声功率谱密度（Rosat and Hinderer,2018）.重力仪的噪声一般在地震频段高于NLNM，而在次地震频段，一些高精度重力仪（如超导重力仪）的噪声水平可以低于NLNM（张苗苗等,2021）.本研究主要探讨各重力仪在不同实验场地的次地震频段功率谱密度.

本研究以指数坐标系表示功率谱密度，因此潮汐、非线性项和不规则项这3种信号功率谱密度曲线的上包络线可视作重力信号gi的功率谱密度.无论是淮北重力站实验（图7）还是淮南地下实验（图8），各仪器的重力功率谱密度曲线均与Rosat等（2018）的观测结果非常接近，整体上随频率的增大功率谱密度逐渐减小，在24 h、12 h和8 h周期处各有1个波峰.这3个波峰的能量主要来自潮汐信号ti，分别对应周日波、半日波和三分之一日波，这些信号的能量占重力信号总能量的90%左右（Fores et al.,2017）.重力仪噪声分析主要是对扣除了潮汐的重力信号进行功率谱密度分析，本研究的非线性项和不规则项曲线的上包络线称为非潮汐项功率谱密度，在潮汐频段以外可以近似地看作噪声功率谱密度.但由于本研究并未进行9阶多项式扣除，因此非潮汐项功率谱密度在潮汐频段高于噪声功率谱密度.需注意的是，潮汐信号的扣除是目前尚未完全解决的难题，无论是调和分析方法还是合成潮方法，残差在24 h、12 h和8 h周期附近依然会保留些许波峰（Imanishi et al.,2004;Rosat et al.,2018）.本研究在潮汐分析过程中利用随机游走模型拟合非线性项，而非直接进行9阶多项式扣除，但非线性项依然在一定程度上残留了周日、半日和三分之一日的波峰.这种潮汐信号的残留与仪器观测水平有关，CG-6型重力仪残留的波峰形态比CG-5型明显，而观测性能更好的超导重力仪不仅波峰形态比本研究的两种弹簧重力仪更明显，而且波峰的宽度更窄，能量更集中（Rosat et al.,2018）.即优先根据主要潮波残余信号的幅值判断潮汐扣除效果，再根据残余信号的形态判断剩余信号中是否仍包含具有能量集中的信号.

非线性项能量是否集中在24 h、12 h和8 h周期也反映了仪器的噪声水平.以CG-5型333号仪器为例，其非线性项功率谱密度在24 h和12 h周期之间有一个较大的波峰，在淮北重力站实验中该波峰超过了潮汐信号（图7c），其非线性项的幅值也非常大（图4c）；在淮南深地实验中该波峰与潮汐信号基本一致（图8c），该仪器的非线性项幅值也大幅缩小（图5c）.可见功率谱密度分析的结果也表明重力仪在井下巷道深地环境的观测性能优于山洞.各仪器的非常规项在形态上与非线性项均非常一致，只是量级上存在较大差异，这是因为本研究的非常规项是由重力信号扣除潮汐信号和非线性项得到的，因此非常规项和非线性具有很强的相关性.尽管非常规项由数学模型得到，不具有物理意义，但其功率谱密度在形态和量级上都与张苗苗等（2021）的噪声非常接近.本研究主要以非线性项作为噪声水平的研究对象，因为非线性项包含了非线性漂移这一能够衡量观测性能的信号.

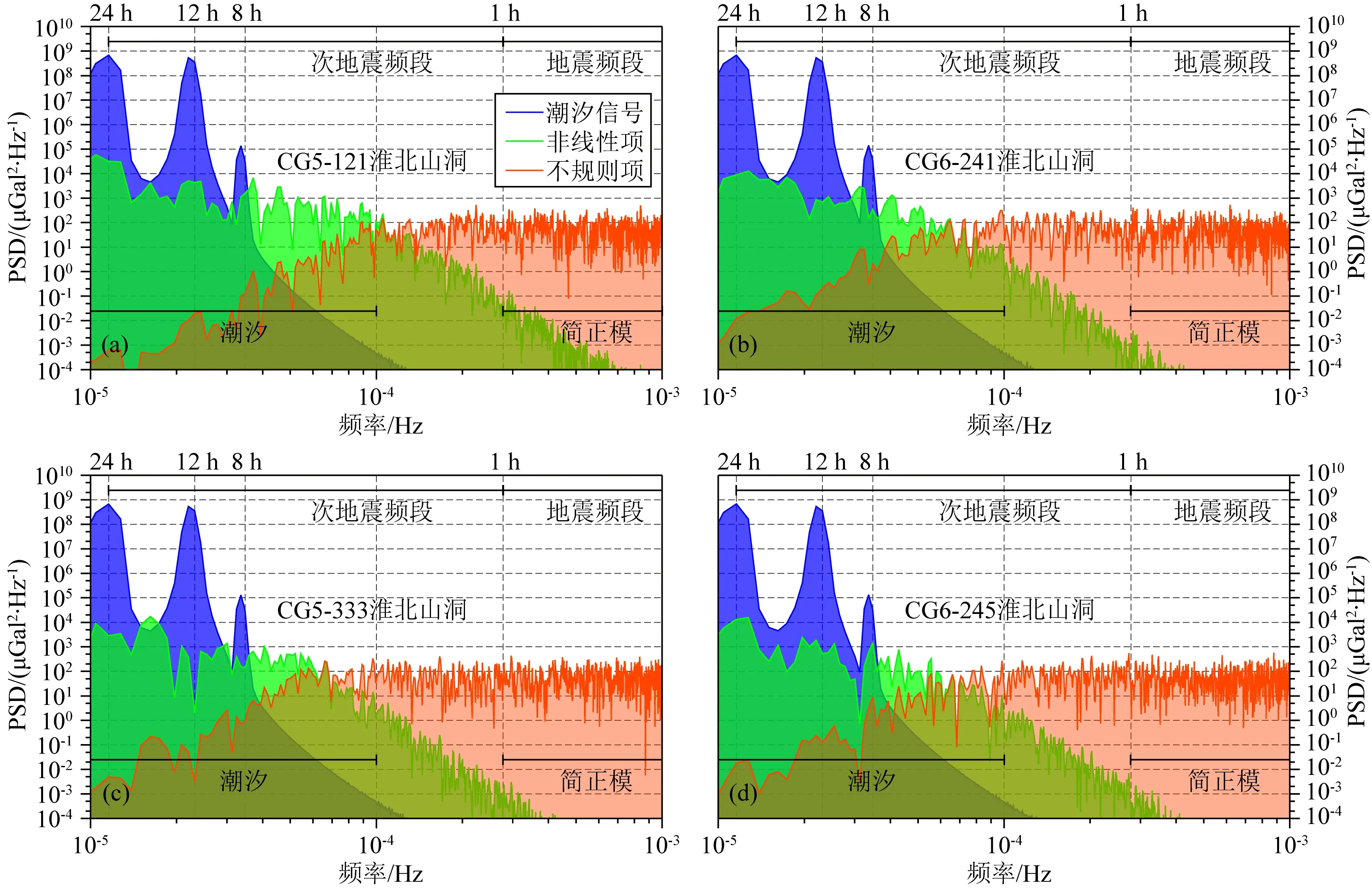
图7 淮北重力站各重力仪数据功率谱密度结果（a） CG-5型121号仪器；（b） CG-6型241号仪器；（c） CG-5型333号仪器；（d） CG-6型245号仪器.蓝线、绿线和红线分别表示潮汐信号、非线性项和不规则项.Fig.7 Power spectra density results of gravity observation at Huaibei cave（a） No.121 CG-5 gravimeter;（b） No.241 CG-6 gravimeter;（c） No.333 CG-5 gravimeter;（d） No.245 CG-6 gravimeter.Blue,green,and red lines denote tidal signal,non-linear term,and irregular term,respectively.

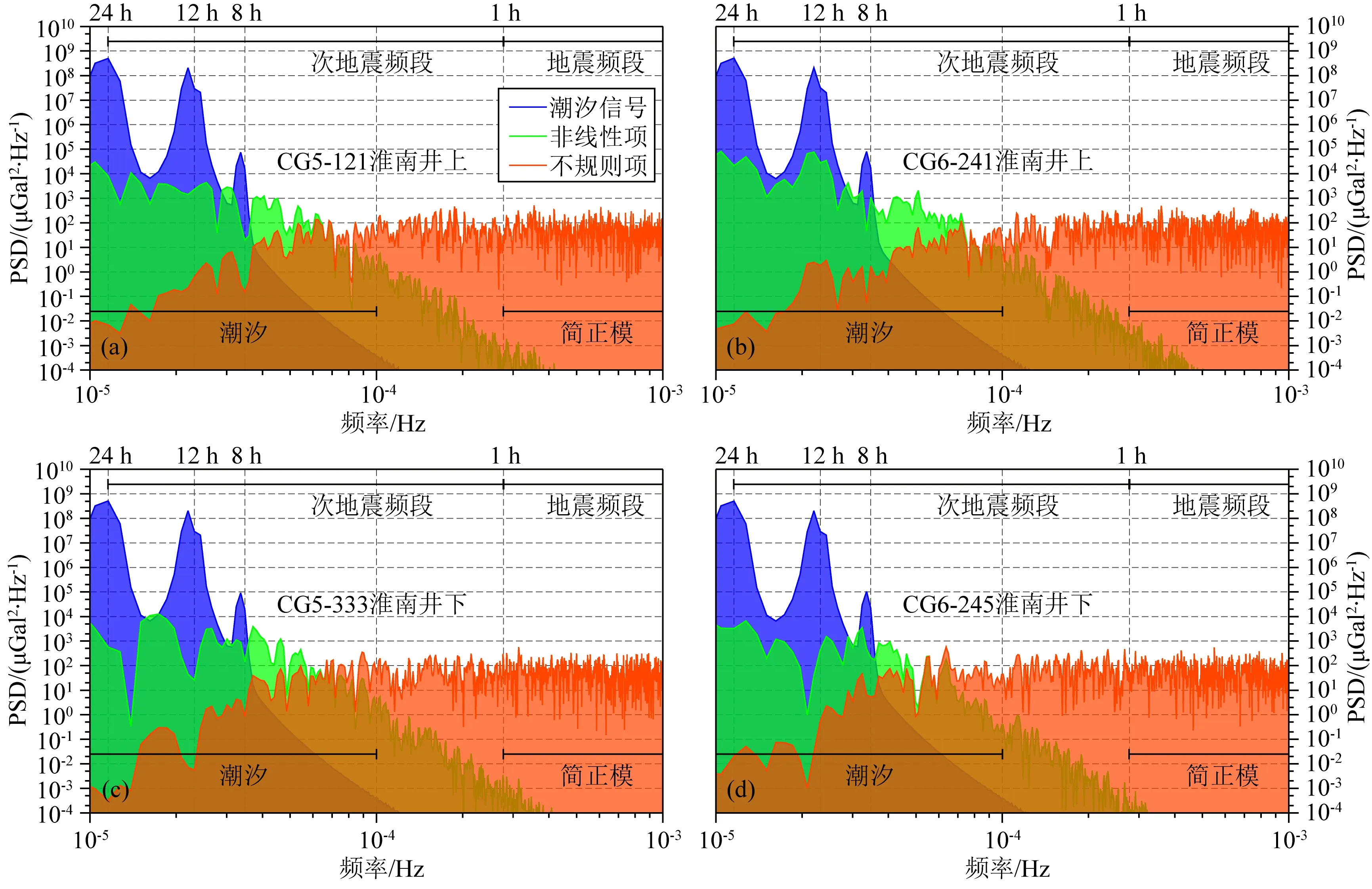
图8 淮南矿井各重力仪数据功率谱密度结果（a） CG-5型121号仪器；（b） CG-6型241号仪器；（c） CG-5型333号仪器；（d） CG-6型245号仪器.蓝线、绿线和红线分别表示潮汐信号、非线性项和不规则项.Fig.8 Power spectra density results of gravity observation at Huainan mine（a） No.121 CG-5 gravimeter;（b） No.241 CG-6 gravimeter;（c） No.333 CG-5 gravimeter;（d） No.245 CG-6 gravimeter.Blue,green,and red lines denote tidal signal,non-linear term,and irregular term,respectively.

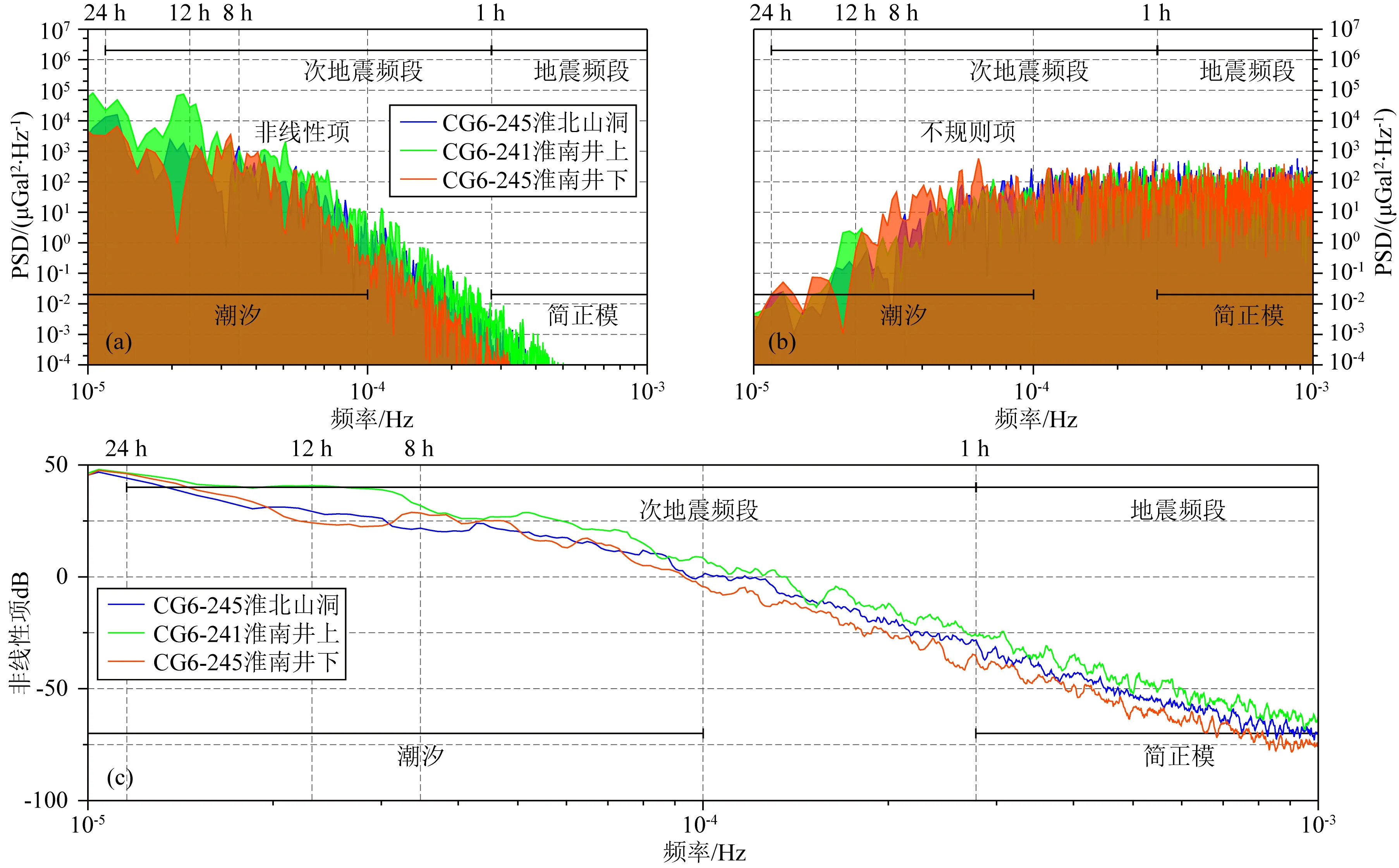
图9 CG-6型重力仪在不同实验场地的观测结果对比（a） 非线性项功率谱密度；（b） 不规则项功率谱密度；（c） 非线性项相对于1 μGal2·Hz-1的dB值.蓝线、绿线和红线分别表示245号仪器淮北重力站观测、241号仪器淮南地表观测和245号仪器淮南井下巷道观测.Fig.9 Gravity observation of CG-6 gravimeter at various locations（a） Power spectra density of non-linear term;（b） Power spectra density of irregular term;（c） dB values of non-linear term relative to 1 μGal2·Hz-1.Blue,green,and red lines denote No.245 gravimeter at Huaibei cave,No.241 gravimeter at Huainan mine （surface）,and No.245 gravimeter at Huainan mine （underground）,respectively.

为了进一步分析同类型仪器在不同实验场地的观测性能，本研究将CG-6型重力仪在淮北重力站、淮南地表和淮南井下巷道地下观测的非线性项和不规则项的功率谱密度进行对比（图9）.根据淮北重力站同址观测的潮汐分析结果，可以判定CG-6型重力仪的性能优于CG-5型重力仪，而两台CG-6型重力仪的性能基本一致，这保证了对比结果的可靠性.从非线性项的结果来看（图9a），在潮汐频段内，3个实验场地均有较明显的半日波峰，而淮南地表的半日波峰量级最大，说明其噪声是3个场地中最大的.在潮汐频段以外，淮南地表的功率谱密度最大，淮北重力站次之，淮南井下巷道深地最小，说明淮南地表的非潮汐噪声最大，淮北重力站次之，淮南井下巷道深地的噪声最小.3个场地的不规则项功率谱密度在潮汐频段内外都混杂在一起，很难区分（图9b），这是由不规则项是根据公式（5）计算导致的.

图9c所示结果为非线性项相对于1 μGal2·Hz-1的dB值，即10log10（PSD）.淮南地表观测的非线性项始终是3个实验场地（地表、山洞和井下）中最大的，由于本研究观测时段较短，可以假定非线性项完全是由非线性漂移导致的，即山洞和井下巷道深地的观测环境都比地表安静.3个实验场地的差异在12 h周期处最大，地表的非线性漂移比井下巷道和山洞高10 dB至15 dB，这解释了地表仪器的M2因子观测精度为何低于井下巷道和山洞的精度（图6）.井下巷道观测和山洞观测的噪声水平对比需要分为两部分描述，在潮汐频段二者基本相当，但在几个主要周期互有高低.在24 h周期处（周日波），二者基本一致；在12 h周期处（半日波），山洞观测的非线性漂移比井下巷道观测高5 dB左右；在8 h周期处（三分之一日波），山洞观测的非线性漂移比井下巷道观测低8 dB左右；在其他频率处2个实验场地的dB值曲线大致重合.在潮汐频段外，山洞观测的非线性漂移在各个频率都大于井下巷道观测，差异为数dB.

需要再次说明的是，由于本期重力观测时间仅有10天左右，难以提取淮南深地实验室最平静时段，只能对山洞、地表和深地观测结果进行对比，给出三者非线性项的相对大小（图9c）.后续研究将在淮南深地实验室开展长期连续重力观测，力争获取淮南深地实验室噪声水平的绝对范围.

4 讨论与结论

4.1 对慢地震监测的潜在应用

根据潮汐分析和功率谱密度分析的结果，井下巷道观测在次地震频段相较于地表或山洞观测具有明显的低噪声的优势，因此在对慢地震的监测方面有巨大的应用前景.慢地震是地震的长周期表现形式，其发震时间可达数十小时甚至数十天.由于超过了地震仪的观测频段，慢地震在过去被认为是安静而无法被监测到的，直到Rogers和Dragert（2003）发现期幕式震颤地震信号和大地测量观测的慢滑移事件存在对应关系，才打开了利用宽频地震仪和大地测量仪器（应变仪、倾斜仪和重力仪等）研究慢地震的新窗口（Melbourne and Webb,2003;Zhang et al.,2008;Shen et al.,2011）.伴随慢地震的慢滑移会导致断层面上的局部应力产生变化，进而促使尺寸较小的裂隙破裂，单个破裂难以观测，但这些破裂的叠加会形成可观测的低频震颤信号（Ito et al.,2007）.当足够多的慢滑移事件使断层闭锁达到一定程度后，大地震发生的概率将大大增加，因此监测慢地震对于地震灾害防御具有重要作用（Shelly et al.,2006）.

目前发现的慢地震现象多集中于日本海沟、卡斯凯迪亚和墨西哥等俯冲带地区，与地幔楔的高孔隙流体压力结构有关（Miller et al.,2002;Gao and Wang,2017;Plata-Martinez et al.,2021）.尽管慢地震几乎没有地震波辐射，但其释放的能量与常规地震释放的能量基本处于同数量级，而且慢地震同样具有地震矩（Beroza and Jordan,1990）.日本海沟是目前观测手段最丰富、近场台站分布最密集的地区之一（Shelly et al.,2006），多次观测到地震矩达到7级左右的慢地震信号（Schwartz and Rokosky,2007）.冲绳海沟与日本海沟总体构造条件与运动特性类似，具有产生慢地震的形成环境与加载条件，但由于近场缺乏密集的GNSS等台站观测，迄今为止尚未见到冲绳海沟慢地震的报道.淮南地下实验室的建成有望为冲绳海沟慢地震事件的监测与远场效应研究提供高精度观测支持（图1）.

为了确定淮南深地观测对冲绳海沟慢地震是否具有监测能力，本研究计算了一个假定的冲绳海沟7.0级地震引起的淮南地表和地下871 m深度（巷道深度）的重力变化，以及地表水平位移.该假定地震的震源机制解参考2022年3月18日发生在琉球群岛的一个5.9级地震，但震级调整为7.0级.该地震震中位于北纬25.671°，东经123.988°，震源深度165.9 km（https:∥earthquake.usgs.gov/earthquakes/eventpage/us6000h5uk/executive）.结合震级与断层尺度的经验关系构建位错模型（Wells and Coppersmith,1994）.地球分层介质参数参考PREM模型（Dziewonski and Anderson,1981），然后利用球体位错理论（Sun and Okubo,1993）计算该假设地震在淮南深地实验室引起的同震位移与重力变化.计算结果表明，该地震引起的地表水平位移为0.027 mm，地表重力变化为-0.0023 μGal，地下重力变化为-0.0031 μGal.中国大陆GNSS观测的水平位移探测精度为2～4 mm，无法约束冲绳海沟的慢地震事件.精度为10 μGal左右的CG-6型重力仪与Burris型重力仪，以及gPhone型连续重力观测仪器，同样无法探测冲绳海沟7级左右的慢地震事件.静态观测精度为0.001 μGal的超导重力观测（Rosat and Hinderer,2011）有可能探测冲绳海沟的慢地震事件引起的重力变化，但如此微弱的重力变化若在地表进行观测势必被环境噪声所淹没，只有在深地超静环境下进行观测才有可能被成功识别.基于以上论述，若要成功捕捉冲绳海沟发生的7级左右的慢地震事件，需使用精度更高的超导重力仪进行观测，同时配以超静的观测环境.淮南煤矿的深地实验室为上述观测研究提供了理想的观测场所，但具体效果还需要进一步的研究验证.

此外，慢地震引起的重力变化有别于常规地震，常规地震的发震时间通常只有数十秒，对于重力仪而言几乎是瞬时的信号变化，在时域内表现为阶跃；而慢地震的发震时间可达数十小时甚至数十天，在时域内表现为非潮汐变化或非线性漂移，因此仪器的非线性漂移越小，对慢地震的监测能力越强.根据同类型重力仪在山洞、地表和井下巷道的表现，以CG-6型重力仪为例，井下巷道的非线性漂移量值最小（比其他场地小1/3左右），变化最平缓，最适合监测慢地震.而在频域内，慢地震释放的能量主要分布在次地震频段，该频段内井下巷道和山洞的噪声均低于地表，最大差值可达10 dB至15 dB，而井下巷道的噪声在大部分频段低于山洞.综上所述，井下巷道观测具有最安静的特点，是目前监测冲绳海沟慢地震的最理想场地，若结合高精度的绝对或超导重力仪，则有望利用重力变化信号捕捉冲绳海沟7级以上的慢地震事件.

4.2 结论

本研究利用CG-5型和CG-6型各两台弹簧重力仪，分别在陆态网络淮北重力站和淮南煤矿开展了为期10天的静态重力观测，并对观测数据进行了潮汐分析和功率谱密度分析.研究结果表明相对于地表观测，地下观测可以减少1/3至1/2的线性漂移.潮汐分析的结果表明地下观测的非线性漂移比地表小1/3左右，调和分析得到的潮汐因子精度更高，对于M2因子可以从0.00458提升到0.00258.功率谱密度分析的结果表明，山洞和地下的观测环境均比地表安静，非线性漂移可以降低10 dB至15 dB左右.在潮汐频段内，地下的周日波非线性漂移与山洞基本一致，半日波比山洞低5 dB左右，三分之一日波比山洞高8 dB左右.在潮汐频段外，地下的非线性漂移整体低于山洞.

此外，本研究利用球体地球地震位错理论展开模拟计算研究，发现冲绳海沟7级左右地震可在淮南煤矿深地环境产生-0.003 μGal的重力变化，信号非常微弱，但明显超过超导重力观测0.001 μGal的静态观测精度.因此，利用淮南深地实验室在次地震频段的低噪声优势开展超导连续重力观测研究，有望探测冲绳海沟7级以上的慢地震事件.

致谢感谢编辑和审稿专家的辛勤付出，感谢所有参与重力观测的工作人员，感谢军事科学院与淮河能源（集团）股份有限公司、安徽理工大学对观测期间安全保障与设备维护提供的大力支持和便利条件.图件由GMT软件绘制（Wessel and Smith,1998），地形数据来自srtm高程数据集（https:∥doi.org/10.1029/2019EA000658）.