电压源型双馈风电机组次同步振荡抑制方法

张澳，代林旺，马政阳，李少林，张学广

（1.哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001；2.中国电力科学研究院有限公司新能源与储能运行控制国家重点实验室，北京 100192）

随着化石能源的利用，全球变暖和环境污染问题正逐渐加剧，因此风能的开发成为目前研究的热点。目前风力发电大多采用双馈风电机组（doubly-fed induction generator，DFIG），其控制方式有两种，比较成熟的是传统矢量控制方式，但随着风电在电网中比例的增加，其无法支撑电网的劣势也逐渐明显[1]。采用电压源型控制方式可以很好地解决这一问题。在实际应用中，大多需要在输电线路中串联补偿电容以提高输电能力，但其可能会导致次同步振荡（sub-synchronous os⁃cillation，SSO）现象的产生[2]。因此十分有必要对并网时次同步振荡问题进行分析[3-4]。

电压源型控制方式主要通过虚拟同步发电机（virtual synchronous generator，VSG）控制策略来实现，文献[5]将VSG技术引入到DFIG的转子侧控制中，起到了对电网的频率与电压幅值支撑效果。文献[6]将VSG控制分为两类，一种是直接通过虚拟同步方式获得转子电压d，q轴控制信号的直接电压控制方式，另一种为通过虚拟同步方式获得定子电压d，q轴信号，再经过电压电流内环得到转子电压d，q轴信号的间接电压控制方式。文献[7]对电压电流内环进行了改进，通过引入虚拟阻抗的方式对输出阻抗进行控制，同时将输出功率解耦。文献[8]在虚拟同步控制中引入二阶广义积分器以简化控制结构。

并网时电力电子器件小扰动对电力系统可能会造成稳定性的问题，常用的分析方法有两种，分别为特征值分析法与阻抗分析法。特征值分析法是对系统的状态空间模型计算特征矩阵与特征根，通过分析根轨迹、参与因子和阻尼比来对系统的稳定性进行判断；阻抗分析法不关注系统内部各部分结构，通过外部输入输出特性建立系统频域阻抗模型，根据广义奈奎斯特判据（generalized Nyquist criterion，GNC）分析曲线是否包围（-1，j0）点来对稳定性进行分析。对于DFIG系统，通常采用阻抗模型进行分析[9]。文献[10]建立了DFIG系统的统一阻抗模型，推导出了输出点与并网点的阻抗关系。文献[11]建立了考虑控制延时与采样滤波器的负荷虚拟同步机阻抗模型，通过GNC得到了系统在弱电网环境下容易失稳的结论。

针对由于串补电容可能会导致的SSO等问题进行稳定性分析，文献[12]研究了DFIG控制器与次同步谐振电路之间的相互作用，提出了采用陷波器与附加阻尼方式的次同步抑制方法；文献[13]分析了虚拟同步发电机的振荡机理，并虚拟电阻方法提高串补情况下的稳定性；文献[14]提出一种采用避开谐振点、提高电气阻尼的方法对SSO问题进行抑制。

目前很少有文献针对VSG控制下的DFIG系统建立阻抗模型，对其的SSO问题分析也较少。本文首先建立了在串补条件下的VSG控制DFIG阻抗模型，并对改变控制参数时输出阻抗的变化进行了研究。基于建立的模型通过GNC分析串补度、阻尼系数与惯性时间常数等对系统稳定性的影响，根据导致SSO发生的原因提出了改进方法对振荡加以抑制，最后通过仿真的方式进行分析，验证了控制的可行性与有效性。

1 VSG-DFIG系统阻抗建模

1.1 VSG控制原理

图1为双馈风电机组在串补电网下虚拟同步机控制结构图。

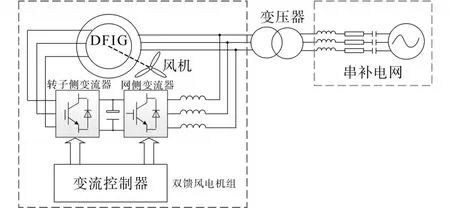
图1 双馈风电机组经串联补偿电网并网系统结构图Fig.1 Structure diagram of grid-connected system of DFIG via series-compensated grid

图2为虚拟同步控制结构框图，通过对有功功率进行控制可以得到电网的虚拟同步角频率，对无功功率进行控制可以得到转子电压的幅值，将二者进行矢量合成便得到了转子电压信号。

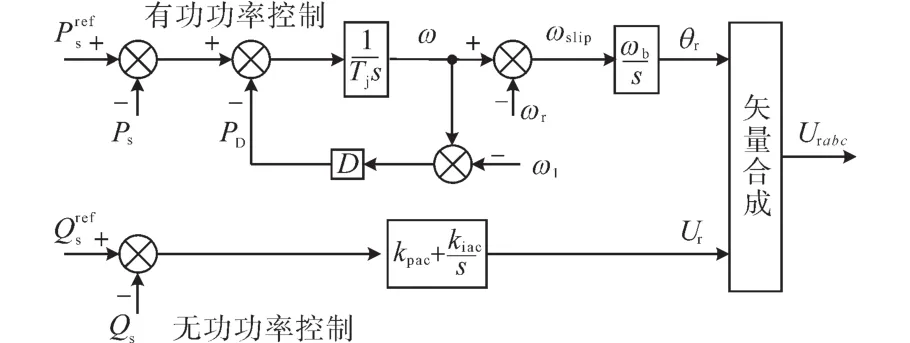
图2 转子侧虚拟同步机控制结构图Fig.2 Structure diagram of the rotor-side VSG control

有功功率控制是通过传统同步发电机的转子运动方程得来的。

有功功率控制方程为

式中：ω1为电网角频率。

无功功率控制方程为

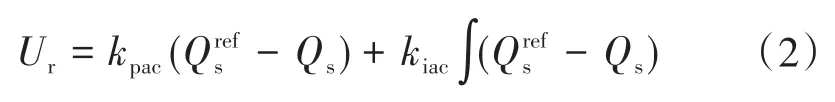
1.2 串补电网下阻抗建模

在串补电网下建模时，需要考虑等效电阻Rg、等效电感Lg和串补电容Cg。根据线路关系可以得到系统三相静止坐标系下的数学模型为

式中：ea，eb，ec为无穷大电网电压；ua，ub，uc为并网点电压；ia，ib，ic为并网点电流；uca，ucb，ucc为串联补偿电容上的电压降落；p为微分算子。

为简化分析，忽略电机内部的各种非理想因素。在d，q轴下得到双馈发电机的数学模型为

式中：us,is,Ψs,Ls和Rs分别为定子电压、电流、磁链、电感和电阻；ur,ir,Ψr,Lr和Rr分别为转子电压、电流、磁链、电感和电阻；Lm为定转子互感；d，q分别为d-q坐标系下物理量的d，q轴分量；ω2为转子电量的角频率。

由于同步旋转坐标系下双馈风机的输出阻抗模型已经研究较为充分[15]，本文不再赘述。为了便于模型的推导，本文做了以下规定：在同步旋转坐标系下，x=[xdxq]T,x∈{us,ur,is,ir}，x为各物理量的瞬时值。系统稳定后注入小信号扰动，可以得到如下的公式：

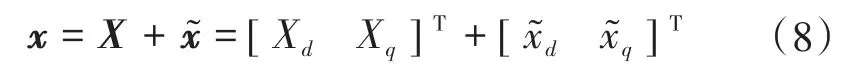
式中：X为各相应物理量的稳态值；x͂为各物理量的扰动值。

可得双馈电机开环输出阻抗[15]为

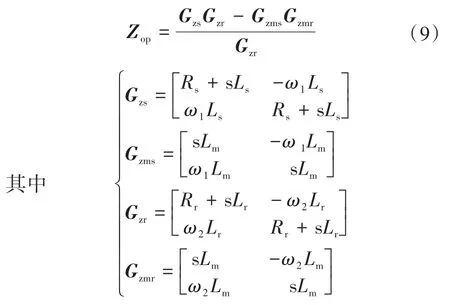
根据虚拟同步控制方程原理可得到矢量合成的励磁电压方程为

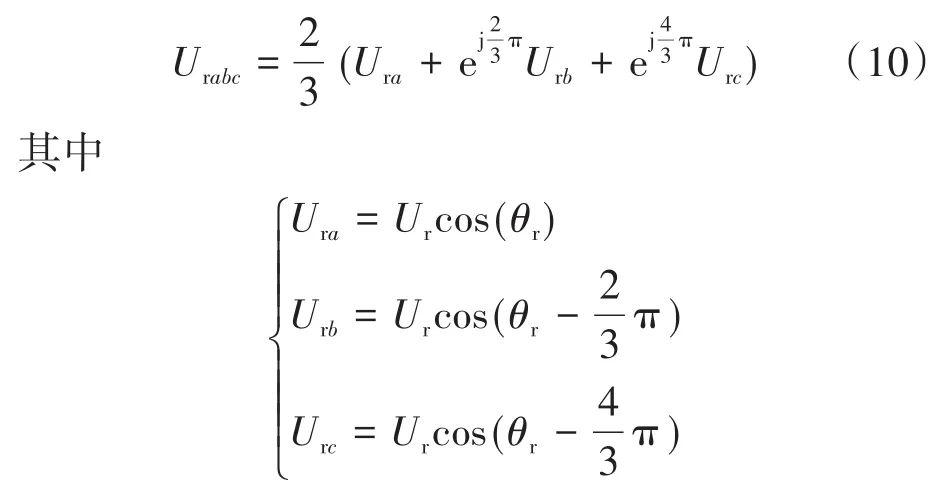
有功和无功功率的表达式为

本文对虚拟同步机控制策略的模拟主要通过有功和无功功率控制实现，因此先对功率表达式进行小信号化。稳态时注入扰动并化简可以得到定子有无功功率的小信号模型：

将有无功功率的扰动量作为输入，将转子电压的幅值与相角的扰动量作为输出，对控制环节进行转换，可以求取虚拟同步控制部分的小信号表达式为

其中

将矢量合成得到的转子励磁电压转换到同步旋转坐标系得：

对其小信号线性化可得其线性化方程为

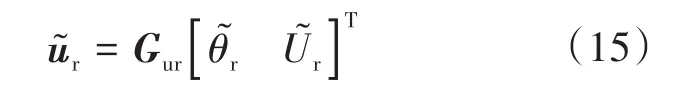
其中

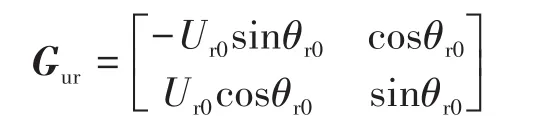
式中：Ur0与θr0分别为转子电压幅值与相位的稳态值。

如果考虑控制系统的延时，则延时传递矩阵Gde可以表示为

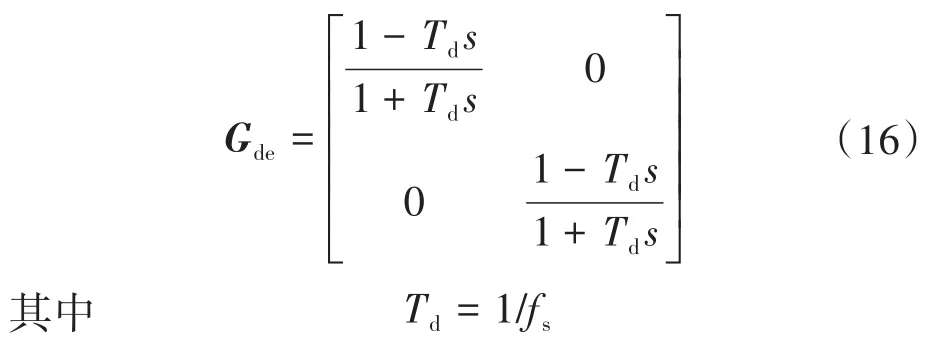
式中：fs为开关频率。

最后得到虚拟同步机控制的DFIG阻抗模型如下：

1.3 双馈风电机组阻抗特性分析

图3为DFIG对应开环与闭环控制下的输出阻抗波德图，开环控制阻抗Zop用虚线表示，闭环控制阻抗Zcl用实线表示。其中dd，dq分量分别为并网点d轴电压扰动与d，q轴电流扰动的比值；qd，qq分量分别为并网点q轴电压扰动与d，q轴电流扰动的比值。

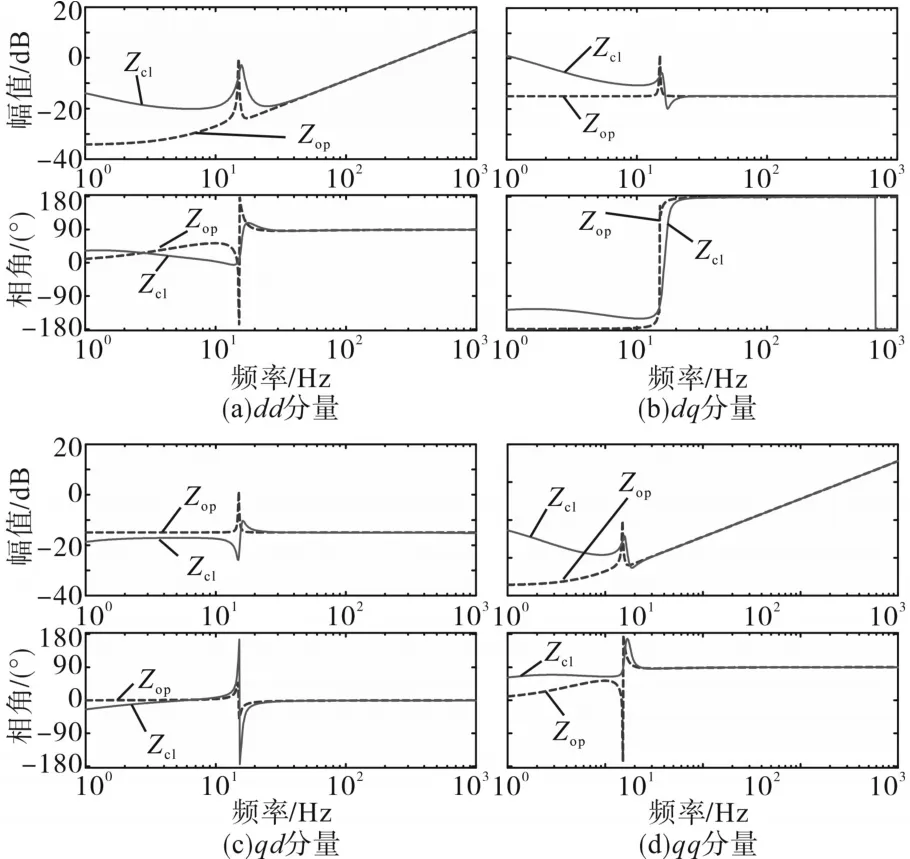
图3 双馈风电机组输出阻抗波德图Fig.3 Output impedance bode diagram of DFIG

由图3可知，当不考虑系统的内部各控制结构时，DFIG开环阻抗中dd与qq分量的幅值与相位均相等，而dq与qd分量的幅值虽然相等，但相位相差180°。因为DFIG本质上是感应电机，因此开环阻抗Zop对外表现为感性。对于考虑电压源型VSG控制时的闭环阻抗Zcl，DFIG在低频段与开环阻抗Zop有较大的差异，而在高频段同样表现出感性。

综上所述，电压源型VSG控制下DFIG的系统参数会很大程度影响系统的输出阻抗特性，结果表明VSG控制参数主要对闭环输出阻抗的低频段起主要影响作用，对高频段的影响基本可忽略不计。建立的阻抗模型为后文对系统进行的稳定性分析打下了理论基础。

2 串补电网下VSG控制的双馈风电机组稳定性分析

进行稳定性分析时所采用的双馈电机以及电网的各项参数设置如下：DFIG额定电压VB=690 V，DFIG基准容量SB=2.1 MV·A，额定频率fB=50 Hz，转子漏感Llr=0.515 2（标幺值），定子漏感Lls=0.293 8（标幺值），转子电阻Rr=0.019 4（标幺值），定子电阻Rs=0.023 8（标幺值），励磁电感LM=14.841 1（标幺值），直流母线电压Vdc=1 080 V，电网电感Lg=1.0（标幺值），电网电阻Rg=0.05（标幺值），电网电容Cg=6.67（标幺值），其中电机的功率等级为2.1 MV·A。采用VSG控制下的各控制器参数设置如下：惯性时间常数Tj=0.22 s，阻尼系数D=20，无功环比例系数kp=0.01，无功环积分系数ki=0.2。

2.1 控制器及电网参数变化时DFIG的稳定性

图4为改变串补度时DFIG系统的Nyquist图。图4a中，系统串补度为20%，此时的特征根轨迹（粗实线）未包围临界点（-1，j0），说明此时系统处于稳定状态。当增加系统串补度时，根轨迹变化为包围临界点，此时系统失稳。由此可知增大串补度会导致系统失稳。

图4 不同串补度下并网双馈风电机组系统Nyquist图Fig.4 Nyquist diagram of grid-connected DFIG in different compensation levels

同理可以得到其它控制参数的影响如表1所示。

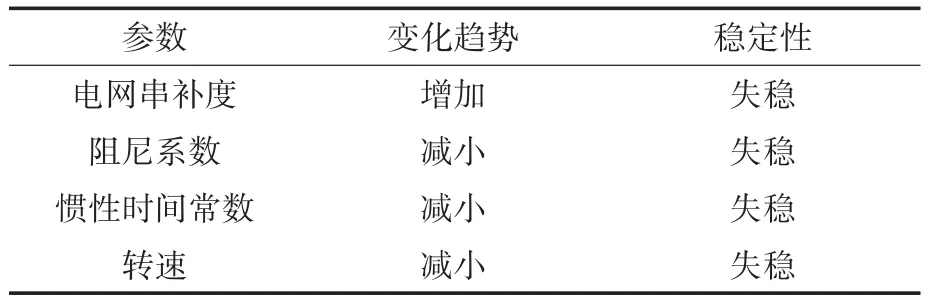
表1 改变各控制参数对系统稳定性的影响Tab.1 Effect of changing each control parameter on system stability

2.2 串补电网下稳定性分析的仿真验证

搭建仿真模型，验证改变系统串补度时系统稳定性的变化。当系统串补度为40%时，系统处于稳定，在2 s时增加系统串补度至65%，系统出现SSO。图5为系统的三相定子电流与无功功率仿真波形，图6为增加串补度后系统三相定子电流FFT结果，可以看到此时系统振荡频率为29 Hz，处于失稳状态，与理论分析结果一致。

图5 增大串补度后三相定子电流与无功功率仿真波形Fig.5 Simulation waveforms of three-phase stator current and reactive power after increasing the compensation levels

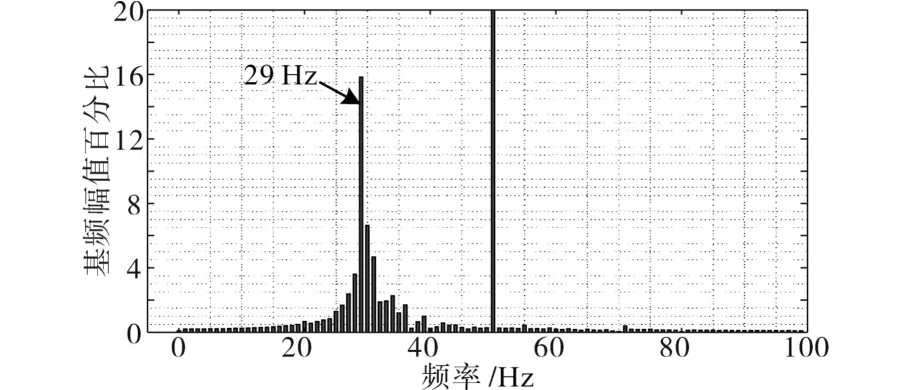
图6 增大电网串补度后双馈风电机组定子电流FFT结果Fig.6 FFT results of V DFIG stator currents after increasing compensation levels

接下来分析控制参数对SSO的影响。首先分析惯性时间常数，当串补度为40%时，系统稳定运行2 s之后将惯性时间常数由0.22 s减小至0.02 s，此时系统产生SSO，图7分别为定子电流与有功功率的振荡波形。通过仿真可以分析出当减小惯性时间常数时，DFIG系统会失去稳定，这与通过阻抗分析的理论结果是一致的。

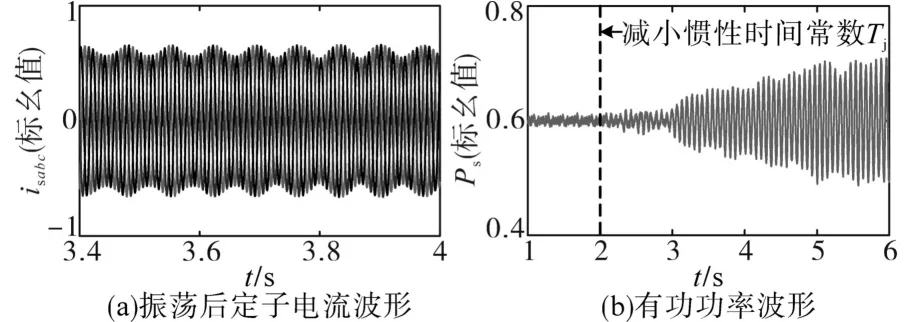
图7 定子电流与有功功率的振荡仿真波形Fig.7 Simulation waveforms of stator current and active power oscillation

采用相同的方法可以对改变阻尼系数时系统稳定性影响进行分析，同样在串补度为40%、系统稳定运行2 s时将阻尼系数从20减小至3.6，发现DFIG系统出现次同步振荡，图8分别为三相定子电流与有功功率波形，可以看出，当减小阻尼系数时，串补并网系统会与阻抗分析结果一样发生失稳现象。

图8 减小阻尼系数后三相定子电流与有功功率仿真波形Fig.8 Simulation waveforms of three-phase stator current and reac⁃tive power after reducing the damping time constant

3 电卾与阻尼协同补偿控制策略

在串补电网下，呈电感特性的DFIG机组与呈电容特性的电网易产生谐振现象。为了抑制SSO的发生，本文提出了一种电压补偿与附加阻尼协同控制策略，控制结构如图9所示，补偿电压采用定子电压经坐标变换后的d，q轴分量，经过二阶带通滤波器乘以补偿系数，与矢量合成后的转子电压信号以及附加阻尼输出信号经过代数运算得到转子电压的输出值。

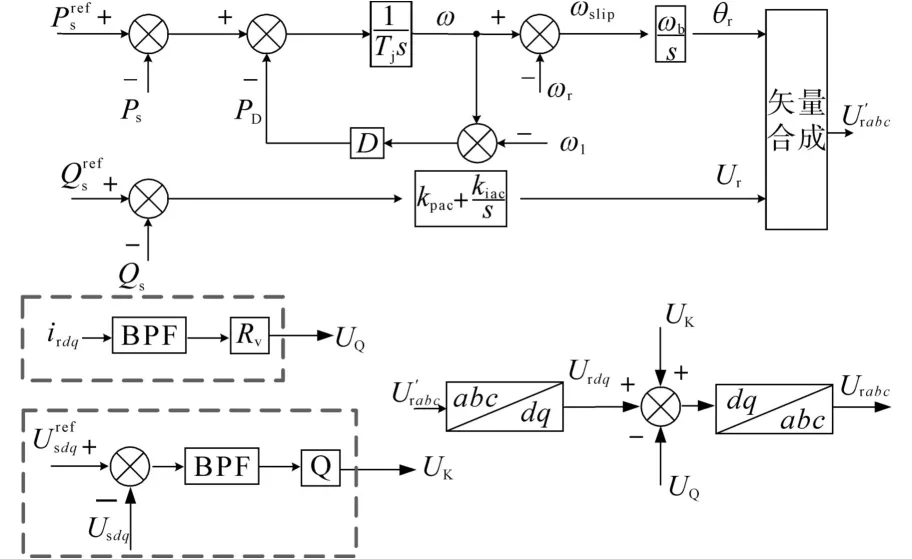
图9 转子侧电压电流内环附加阻尼控制结构框图Fig.9 Block diagram of the rotor-side voltage-current internal loop additional damping control structure

根据图9的附加阻尼控制转子侧电压电流内环控制框图可以得到其数学表达式为

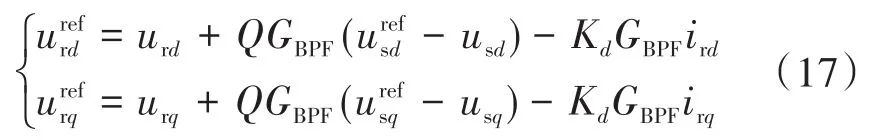
式中：Kd为附加阻尼系数；GBPF为二阶带通滤波器对应的传递函数；Q为电压补偿系数。

附加阻尼控制中采用了二阶带通滤波器，其作用是对信号中次同步分量进行提取，防止直流分量对系统的稳态工作点造成影响。

4 电卾与阻尼协同补偿控制仿真验证

为了对上述控制策略抑制次同步振荡的效果进行验证，将引入策略后新的传递函数与原来的阻抗模型进行合并。引入控制后的方程变为

其中

最后得到附加控制后的阻抗方程为

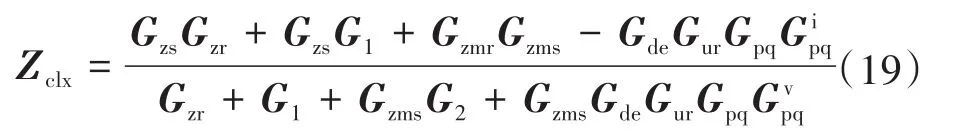
在系统的串补度为65%时对有无控制时DFIG机组稳定性进行分析，系统的的广义Ny⁃quist图如图10所示。

图10 引入附加控制前后系统Nyquist图Fig.10 Nyquist diagram of the system before and after adding additional controls

图10a为没有引入附加阻尼控制时系统的广义奈奎斯特图，此时虚线包围临界点（-1，j0），系统处于失稳状态；图10b为引入控制后系统的广义Nyquist图，此时曲线没有包围临界点（-1，j0），说明引入电压与阻尼协同补偿控制策略之后系统重回稳定状态，该控制策略可以提到系统在串补条件下的稳定性。

设定系统串补度为40%，有无功功率给定分别设置为0.6与0，对比有无附加阻尼时的有功、无功功率波形，如图11所示。

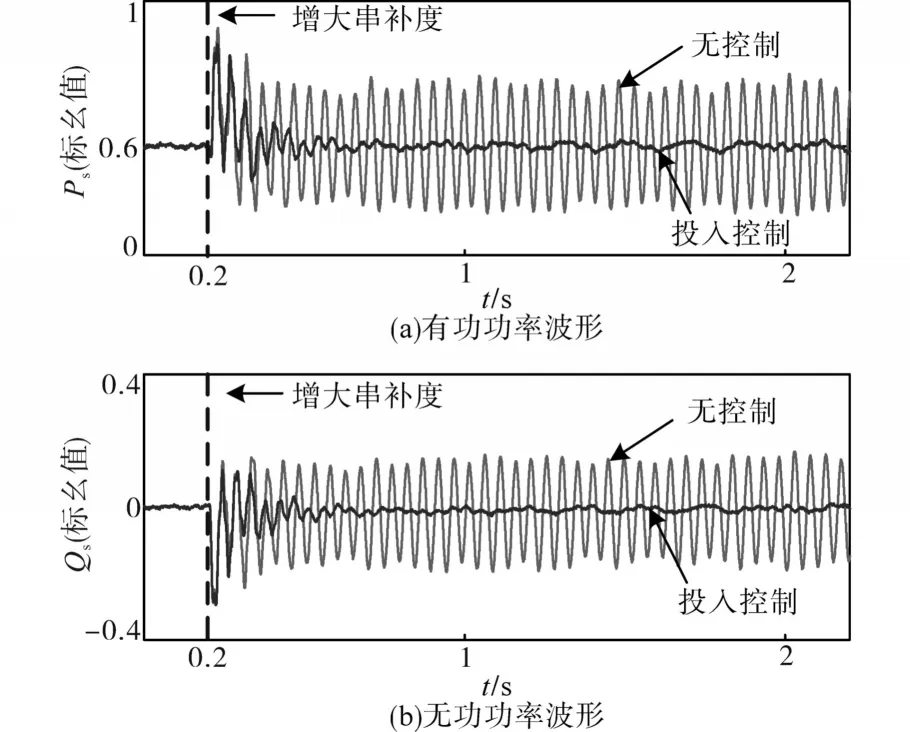
图11 有、无控制下有功、无功功率仿真波形Fig.11 Simulation waveforms of active and reactive power with and without control

图11中，在0.2 s增加串补度至65%，可以看到此时系统产生SSO，而带有协同控制策略下的功率波形可以在较短时间内重新恢复稳定状态，此时的定子电流的THD分析结果如图12所示，为0.85%，在要求范围之内。

图12 协同控制策略下定子电流FFT分析结果Fig.12 Analysis results of stator current FFT under the cooperative control strategy

接着分析若振荡发生一段时间后再投入控制方法，该方法的抑制效果是否理想。在0.2 s时通过改变电网串补度使系统产生次同步振荡，在振荡经过0.8 s后，即在第1 s投入控制。图13a为输出有功功率波形，图13b为输出无功功率波形。可以看到1 s时引入控制后虚拟同步机控制的双馈风电机组输出的有功功率和无功功率波形振荡收敛，并最终趋于稳定，这说明该控制可以有效的抑制次同步振荡。

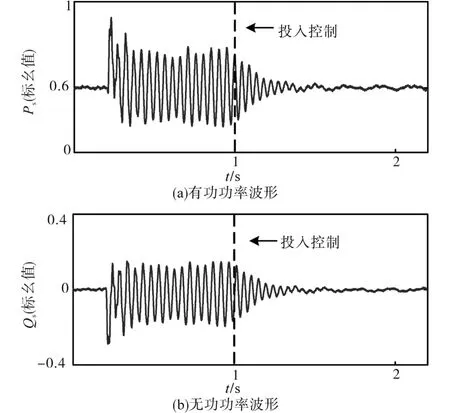
图13 振荡发生一段时间后，有、无控制下有功、无功功率仿真波形Fig.13 Simulation waveforms of active and reactive power with and without control after the oscillation for some time

5 结论

本文研究了串补情况下DFIG机组的次同步振荡问题，首先对电压源型虚拟同步控制下双馈风电机组进行阻抗建模，对其阻抗特性进行分析，可以看出虚拟同步外环各个参数主要对低频段的阻抗特性产生较大影响，随着串补度的增加、惯性时间常数的减小、阻尼系数的减小，串补条件下的DFIG机组就更易出现次同步振荡。通过引入本文提出的电压与阻尼协同补偿控制策略，可以使输出的有功功率和无功功率波形振荡收敛，并最终趋于稳定，有效地抑制次同步振荡，该方法重点解决了串补电网下虚拟同步控制策略的次同步振荡问题，有效地提高了系统性能。