一维残差卷积神经网络的刀具磨损识别方法研究

杨斌,，樊志刚,，王建国,，王民，李志星,

（1.内蒙古科技大学机械工程学院，内蒙古包头 014010；2.内蒙古自治区机电系统智能诊断与控制重点实验室，内蒙古包头 014010；3.北京工业大学机械工程与应用电子技术学院先进制造技术北京重点实验室，北京 100124）

机床刀具作为数控机床的主要末端执行件对于工件表面加工质量、精度有着直接影响，研究表明，尽管机床刀具成本不到加工成本的4%[1]，但由刀具状态异常导致的停机时间占据了总停机时间的10% ～40%[2]。因此，对于刀具磨损状态进行预测对改善加工效率和提高经济效益有着重要作用。同时由于制造过程中影响刀具磨损因素的复杂性、多变性，目前主要采用间接法对刀具磨损状态进行预测，间接法主要是通过采集加工过程信号，对信号进行分析处理提取与刀具状态相关特征信息后，建立与刀具磨损状态的映射关系。常用信号包括切削力、振动、主轴电流以及功率信号等，由于间接法对加工过程的影响较小，在工业领域更受欢迎[3]。

目前深度学习在图像识别[4]、电力负荷预测[5]和故障诊断[6]等工业领域被广泛使用。相比于传统机器学习，深度学习主要是对特征提取和分类过程进行强化，同时自动的从信号中对特征进行提取。近年来，以卷积神经网络（Convolutional neural network，CNN）为代表的深度学习网络目前在刀具磨损状态监测领域已经开展了相关研究。Gouarir 等[7]基于格拉姆角和场（GASF）将力信号转换为二维图像，由分段聚类近似对图像进行平滑和降维处理后使用卷积神经网络对刀具磨损状态进行预测。Aghazadeh 等[8]对电流信号进行小波包时频变换后，使用谱减法将信号中稳态部分去除后作为卷积神经网络的输入，实现了对于刀具磨损的准确预测。张存吉等[9]使用小波包变换处理后的振动信号能量频谱图作为神经网络模型的输入，通过多种网络模型对比发现Wearnet 的效果最佳。但上述研究侧重CNN 对于空间特征的敏感性，使用图像作为输入进行识别时随着网络层数和卷积核数目的增加，预测过程需要的矩阵运算大幅度增加，导致预测效率较低。王丽华等[10]构建了堆叠降噪自编码（Stacked denoising auto encoder，SDAE）网络，基于频域信号样本进行刀具磨损状态识别，显示出频域信号作为输入时的优势。王震等[11]使用多传感器数据直接组合作为输入，基于多尺度卷积神经网络实现对刀具磨损的预测，但未考虑不同信号间量纲不同对于识别的影响。王民等[12]通过傅里叶级数对电流信号进行拟合，将所获电流杂波信号作为一维卷积神经模型输入，实现了对多工况刀具磨损状态的准确预测，但电流杂波未考虑噪声影响。

本文提出了一维残差卷积神经网络的刀具磨损状态监测方法，原始振动信号通过小波包阈值降噪处理后基于快速傅里叶变换（Fast fourier transform，FFT）获得频域数据，将其作为残差连接卷积网络模型的输入，利用残差连接强化前向传播过程中所提取特征密度，有效实现从振动信号中自适应提取刀具磨损的相关特征，避免了传统特征提取过程中人为选择特征导致磨损相关信息的丢失和诊断效率较低的缺陷。

1 残差卷积神经网络简介

1.1 卷积神经网络

卷积神经网络（Convolutional neural network，CNN）是一种特殊的深度神经网络，1984年Fukushima等[13]在感受域的基础上提出神经认知机这一概念，被认为是卷积神经网络正式出现的开端。以典型的卷积神经网络为例，其网络结构如图1所示。

图1典型卷积神经网络模型

图1 中：Input 为输入层；C1、C2分别为2组卷积层；S1、S2为池化层。

在该网络中，每个神经元都与前一层的局部感受域相连接，通过卷积运算和非线性激活获取原始信号中不同层次的特征，从而实现前一层的特征映射，其卷积过程可表示为

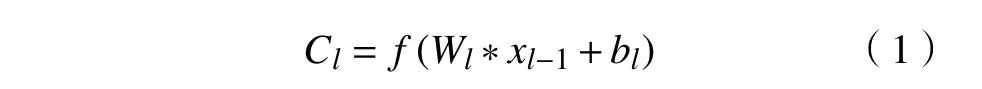
式中：Cl为卷积层输出； f()为非线性激活函数； Wl为第l 层的权值； xl-1为 第l-1层输出；bl为第l 层的偏置。

池化层通过对某一位置的附近区域总体特征进行统计实现了特征选取的多样性和降维，在减少网络参数同时有效避免网络过拟合。本文中采用最大池化，池化过程可表达为

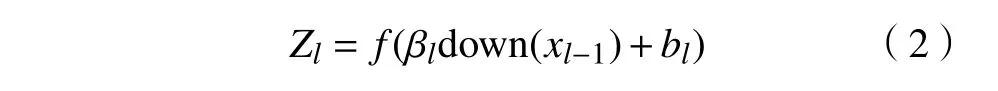
式中： Zl为第 l层 的输出映射； βl为第l 层的采样权值系数； bl为第 l层 的偏置； down()是一个下采样函数。本文中采用最大池化策略。

全连接层对卷积、池化处理后的高维信息特征进行整合，利用线性方程所对应的特征面对输入进行拟合，之后通过Softmax 逻辑回归对信息进行多分类处理，其模型为

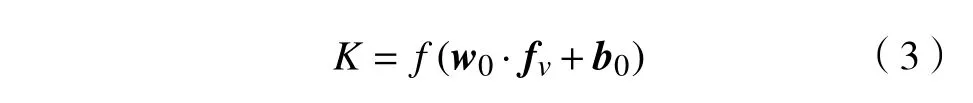
式中： fv为 特征矢量； w0为权值矩阵； b0为偏置矩阵。

1.2 残差块概念

理论上，卷积神经网络模型的结构越深，神经元数目越多，网络的表达程度越高、拟合能力越强，但是随着网络层数的增加，不可避免地产生了梯度爆炸、梯度弥散等问题，导致反向传播训练时效果不佳。因此，2015年He 等[14]提出了深度残差网络模型，采用跳跃连接的网络结构将浅层特征以及深层特征进行叠加，有效避免网络训练时浅层特征的丢失，其残差连接结构如图2所示。

图2残差连接结构

图2 中： x为 当前单元输入， F(x)为通过非线性变换函数处理的当前单元的映射输出，在前向传播过程中，不仅将每个当前单元的映射输出作为下一单元的输入，还将当前单元的输入也直接连接添加到下一单元输入，从而实现了跳跃连接。因此，下一单元的输入为

2 刀具磨损状态识别方法

2.1 数据预处理

在切削过程中，采集的切削振动信号经常包含噪声，因此对于加速度传感器所采集的振动数据需要进行预处理，除去该数据中的无效数据和异常数据。对铣削过程中的原始振动信号进行小波包去噪处理，由于阈值选取和函数选择对于去噪效果有直接影响，针对信号进行合适的选择就显得尤为重要。

切削振动信号属于典型的非平稳信号，小波基的性质与其相关性越好，最终能提取的特征越多[15]。由于Daubechies系列小波基具有正交性、紧支性以及时域波形上的振荡衰减性，本文通过对比试验确定小波基为db8。

常见的小波包阈值选取准则包括：固定阈值式准则（Sqtwolog）、自适应式阈值准则（Rigrsure）、启发式阈值准则（Heursure）和最小极大式阈值准则（Minimaxi）[16]，由于固定阈值可以对所有的小波包系数进行处理，降噪效果较为明显，选择固定准则方

式进行阈值选取，取值公式为

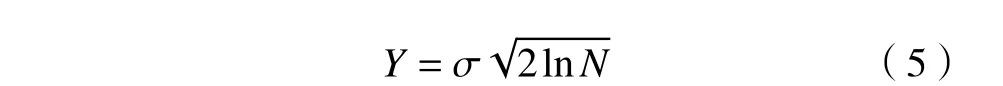
式中： Y 为所估计的阈值； σ为信号标准方差； N为输入信号长度。

同时在工业领域中广泛使用的阈值函数有硬、软阈值函数法，由于硬阈值函数在远离阈值时处理小波包系数效果较好，故选择其作为阈值函数，表达式为

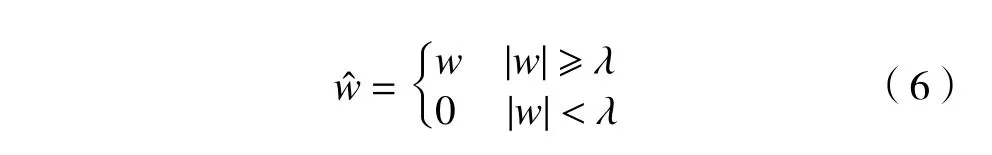
最终小波包阈值降噪效果如图3所示。

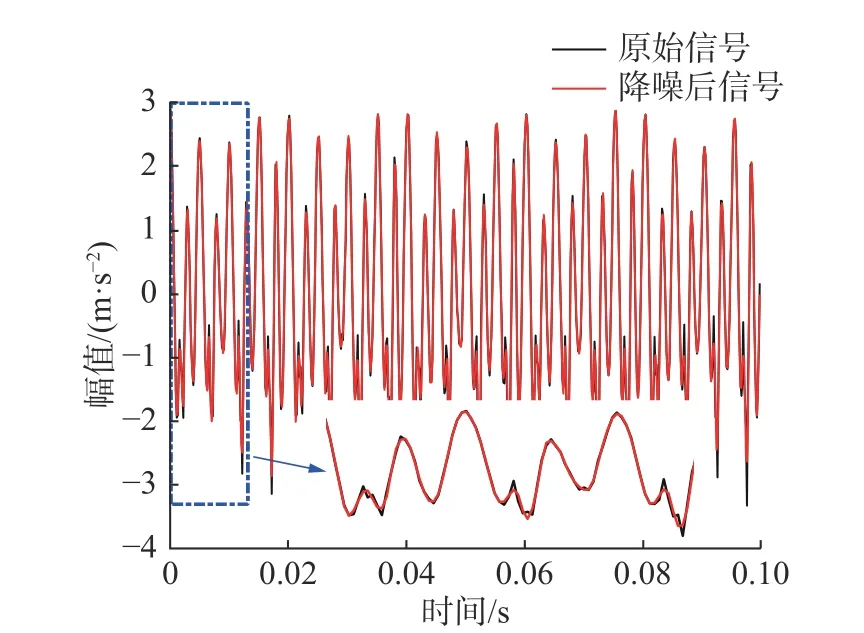
图3 小波包阈值降噪效果

振动信号在时域上可以被视为多个正弦波叠加的结果[17]，通过对振动信号进行频谱分析可以获得信号的频率成分和对应的幅值大小。通过FFT对降噪后信号进行处理，将获取的幅频值作为输入数据，其中FFT 公式为

式中： X(w)为 输入信号x（t）的 连续频谱； w为角频率。经过FFT处理后的幅频图如图4所示。

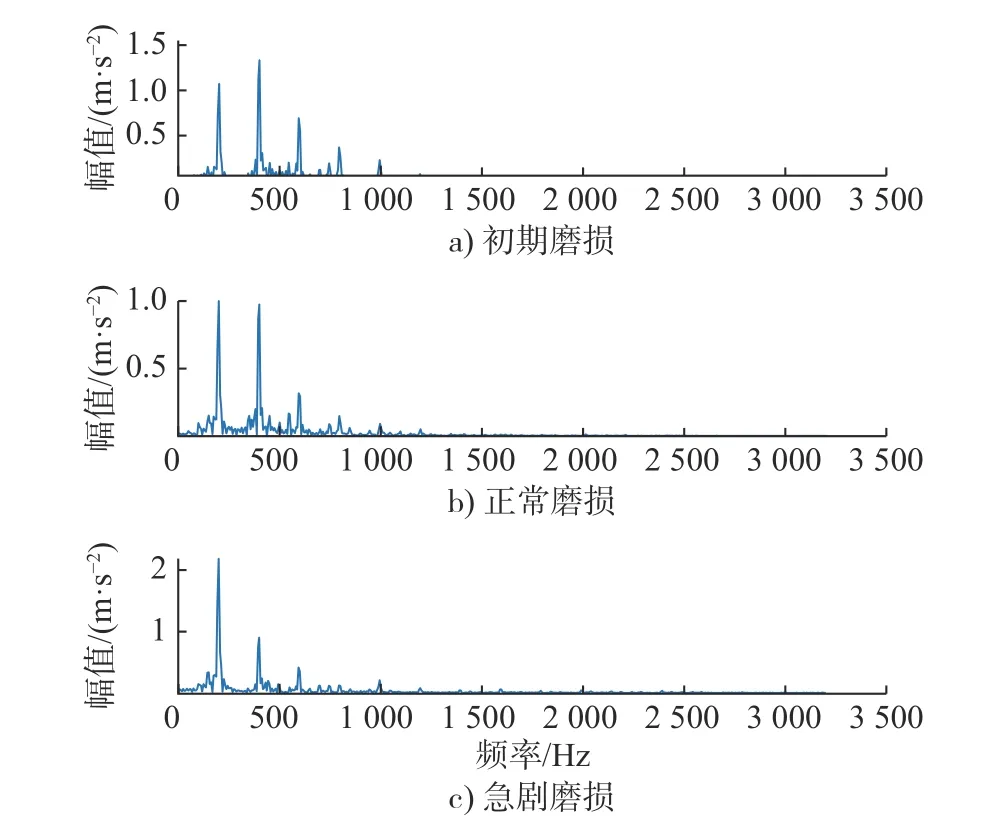
图4 不同磨损阶段的幅频图

2.2 网络结构

传统的深度残差网络主要对于二维图像通过卷积等操作进行识别和分类，由于深度学习需要大量的样本才能保证所学习特征的正确性和结果的准确性，大量图像样本作为输入时所需学习时间较长。本文针对该问题提出了基于刀具磨损振动信号的一维残差连接卷积神经网络，将振动信号进行FFT 处理后的频谱数据作为输入，直接对其进行卷积运算、池化操作、跳跃连接和融合等前向运算等对其进行特征提取，同时通过反向传播对权值、偏差进行调整，最终实现对刀具磨损的最优识别和分类。

本文中对于刀具磨损状态进行监测时借鉴前文中残差连接的设计思路，目的是将输入的信号x 通过卷积操作等映射输出为刀具不同的磨损状态。将刀具磨损状态分为初期磨损、正常磨损和急剧磨损。分类器选择适用于多分类任务的softmax 分类器，同时为了提高网络对的泛化能力，该模型中每个卷积层后都使用Relu 激活函数和BN层对数据进行正则化处理，同时在网络中使用droupout 函数，在每批次训练过程中使一半的隐层节点变为0，防止网络训练过程中出现过拟合现象，通过上述调整，既提高了整个网络的运行效率，又防止了网络训练过程中的梯度弥散、网络退化等现象。

本文采用的网络模型结构如图5所示。将通过FFT 生成的尺寸为1×128的频谱数据（幅频值）输入到残差连接网络，采用卷积核为100×1×9的卷积层C1对输入数据进行卷积，同时通过补零进行边缘扩展来保证卷积层输出大小保持不变，由于不同尺寸的卷积核对输入数据进行特征提取时获取的特征不相同，本文选用不同的卷积核数目进行组合来对卷积层C1输出的高维信息进行获取，其中主通道卷积层C2采用卷积核为50×1×11，由C2输出的特征数据输入到卷积核为1×2的池化层P1中，池化核步长为2，由P1生成的特征数据输入到卷积核为100×1×11的卷积层C3中进行卷积，由C3生成的特征数据输入到卷积核为1×2的池化层P2中，P2生成的特征数据尺寸为100×1×27；副通道将C1输出的特征数据输入到卷积核为100×1×11的跳跃卷积层SC1中，由SC1生成的特征数据输入到卷积核为100×1×9的跳跃卷积层SC2中，采用池化核为1×5的跳跃池化层SP1对输入的数据进行池化，池化步长为4，此时SP1的输出数据尺寸同样为100×1×27，将其与主通道P2生成的特征数据通过Add 层进行融合，将Add 层生成的特征数据输入到卷积核为100×1×11的卷积层C4中，扩展边缘为2，由池化核为1×2的池化层P3进行池化，池化层P3提取的特征信息通过Dropout 层输入到全连接层F中，全连接层输出3类刀具磨损状态后通过Softmax 层对磨损状态进行分类。

图5 一维残差卷积神经网络模型

在一维残差卷积神经网络模型中为了在反向传 播过程中获取到最优权值和偏差，使用了一维动量的随机梯度下降法（Stochastic gradient descent with momentum，SGDM）对网络进行优化，并使用交叉熵损失函数作为代价函数，批处理数目为27，共迭代100次。

3 试验验证

3.1 试验装置

刀具磨损实验在一数控铣床上进行试验，加工材料为Cr12模具钢的矩形工件，尺寸为170 mm×100 mm ×80 mm，切削转速为3000 r/min，进给速度为600 mm/min，切深0.5 mm，切宽4 mm。铣削刀具采用无涂层硬质合金四刃立铣刀，刀具直径为8 mm，铣削过程中不使用切削液。在机床主轴外壁安装加速度传感器，对数控机床铣刀的振动信号进行采集，振动信号采样频率为6400 Hz，图6为刀具磨损状态监测系统结构图。

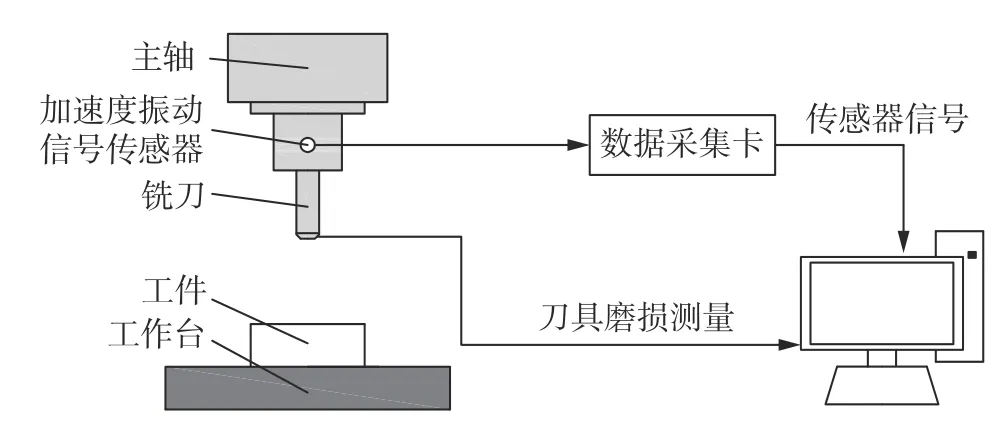
图6 刀具磨损监测系统结构图

3.2 实验数据

采集铣削过程中的振动信号，根据刀具后刀面磨损量划分为初期、正常和急剧磨损3种刀具磨损状态。选取不同阶段切削信号中0.1 s时长数据作为样本，每一走刀过程内选取10个样本，选取其中的70%作为训练数据，剩余的30%作为测试数据，总共选取训练样本966个，测试样本414个。通过对样本进行划分，本试验中建立的刀具数据集基本情况如表1所示。

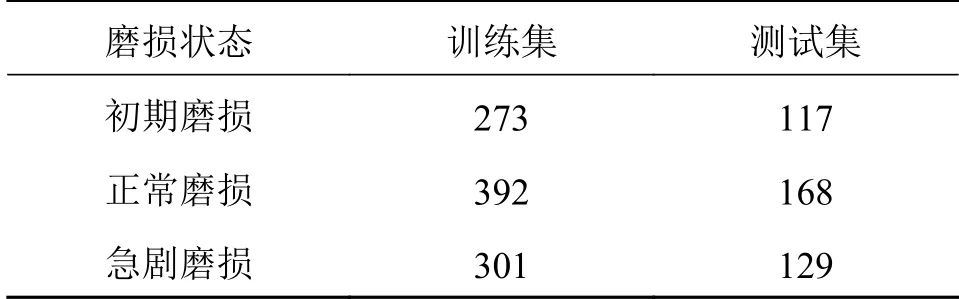
表1 Cr12频谱数据集样本数量

3.3 试验结果与分析

为了验证一维残差卷积神经网络的刀具磨损监测方法的有效性和高效性，使用MATLAB2018搭建网络模型并对该模型进行测试，测试结果如图7所示，其准确率和损失函数能较快达到识别需求，随着训练次数的增加，测试集准确率快速增大达到较高的准确率，并最终趋于稳定，同时损失函数值9次训练后快速收敛到0.05以下，随着训练次数的增加逐渐趋近于0，表明了该网络结构的合理性和优异性。

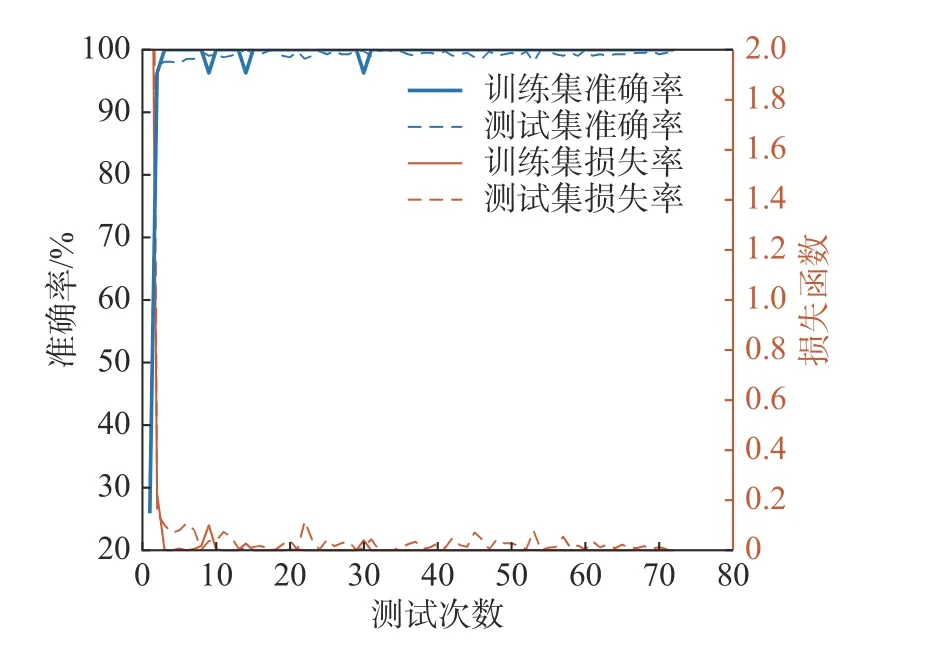
图7 一维残差卷积神经网络训练过程

采用无残差连接的一维卷积网络模型、Alexnet、Lstm 模型以及本文中方法进行对比，其中Alexnet模型使用图片作为输入，其它均使用频域数据进行输入。同时为进一步比较4种模型性能，设置相同的迭代次数，测试结果如表2所示。

表2 不同模型测试结果分析

对比可知，相对于使用图片进行输入，使用一维数据输入所耗时间明显降低，提高了测试效率，虽然本文方法由于残差连接增加了运行时间，但单次迭代所耗时间较为接近。同时为保证测试准确结果的可靠性，对各模型单独训练5次，试验结果如表3所示。

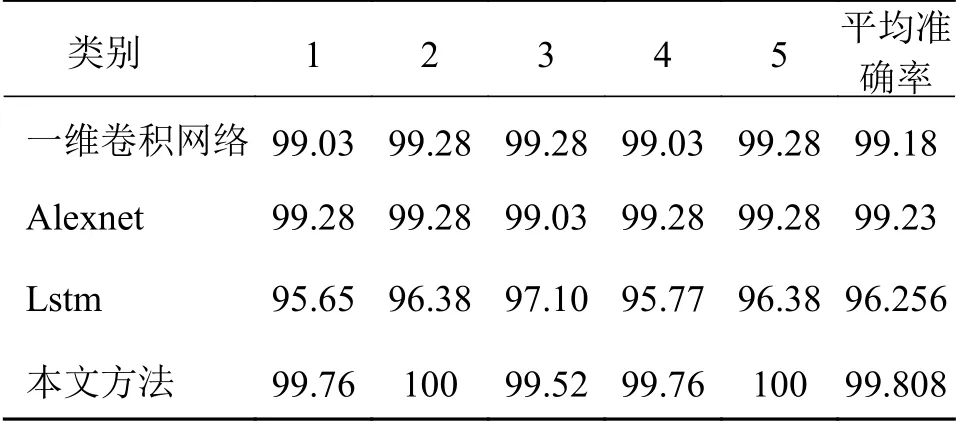
表3 对比试验准确率%

结果表明，以幅频图或频域信号作为输入样本时各模型识别准确率均都达到了95%，取得较好的效果，表明振动信号的频域信号可较全面的反映刀具磨损的相关信息。采用一维残差卷积神经网络模型测试时，整体平均准确率为99.808%，同时多次试验中的识别准确率均大于99.5%，其它方法也有较好的效果，但略次于本文方法。对比结果证明了一维残差卷积神经网络模型优于其他网络模型，表明残差结构可以强化对于刀具磨损相关特征的提取以及该网络模型的优异性。

3.4 方法可适用性验证

为了验证本文方法的适用性，对不同工件及其切削条件进行实验验证。工件材料为45#钢，尺寸为170 mm×100 mm ×80 mm，切削转速为3000 r/min，进给速度为1000 mm/min，切深1 mm，切宽4 mm，采样频率为8000 Hz，切削刀具、样本选取等和切削Cr12模具钢时完全相同。其中训练集为75%，测试集为25%，最终选择训练集样本2718个，测试集样本906个，最终样本划分情况如表4所示。

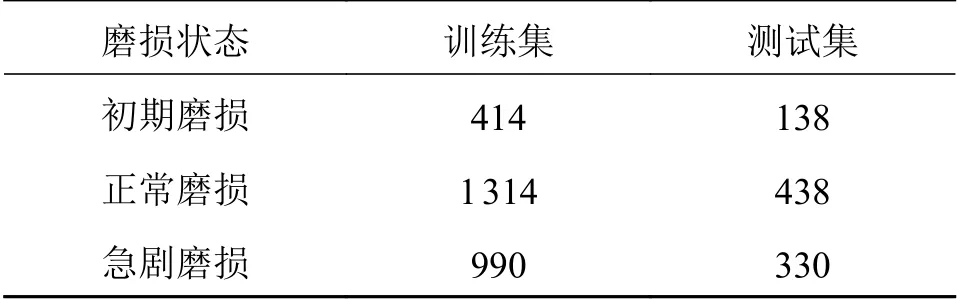
表4 45#钢频谱数据集样本数量

使用该样本作为本文一维残差卷积神经网络的输入进行试验，测试结果如图8所示，可以发现随着测试次数的增加，准确率快速增加并达到90%，然后呈现缓慢上升的趋势，并最终趋于稳定，尽管训练集准确率在初期阶段出现了较大波动，但整体趋势随着训练周期在减小，最终达到完全识别的训练效果，而测试阶段波动幅度较小，最终准确率达到95.47%，同时将结果通过混淆矩阵进行分析如图9所示，纵坐标为预测分类，横坐标为实际分类，3种类别识别准确率分别为98.6%、95.2%和94.5%，表明一维残差卷积神经网络的适用范围较广。

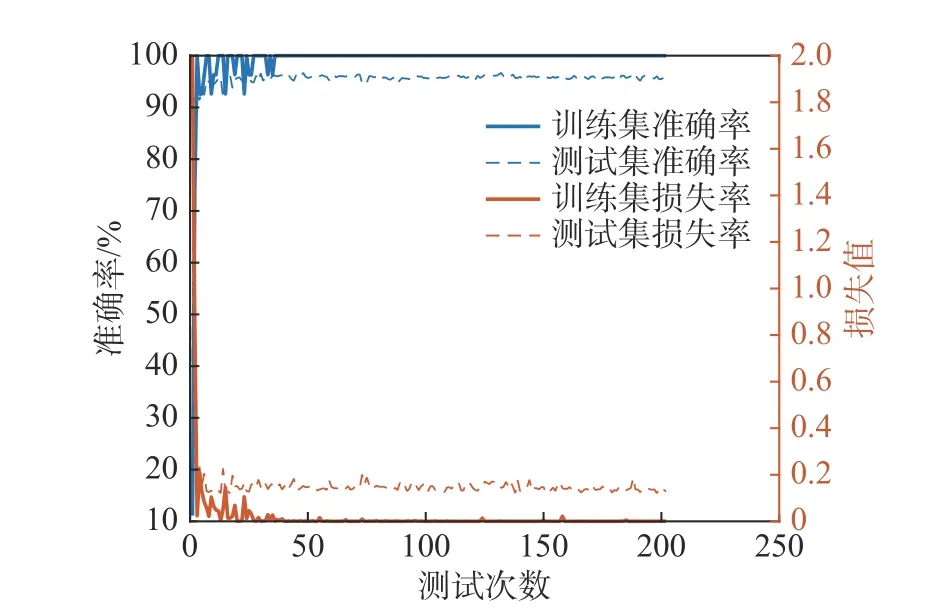
图8 45#钢测试过程曲线

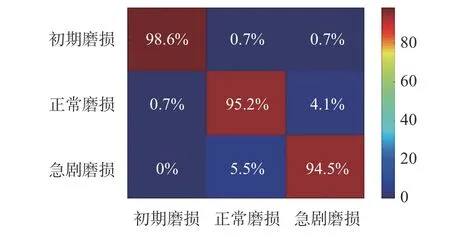
图9 测试混淆矩阵结果

4 结论

本文提出了一种利用振动信号的频域数据在一维残差卷积神经网络模型中实现刀具磨损状态预测的方法，基于刀具不同磨损阶段时振动信号的频域数据幅值呈现明显变化的情况，利用小波包对原始振动信号进行降噪并通过FFT获取信号的频域数据，保证了特征信息的完整性，将其作为一维残差卷积神经网络模型的输入进行刀具磨损状态的预测。结果表明：

1）一维残差卷积神经网络模型可自适应提取频域数据中的刀具磨损相关特征，避免了人工提取的繁琐性。

2）将本文方法与其它方法在耗时性、准确率方面进行对比，发现本文方法的耗时较少并且多次测试后平均准确率最优，表明了本文方法的具有较好的状态预测效果。

3）使用本文方法对不同加工对象和加工条件下方法的适用性进行了验证，结果表明该模型可实现对不同加工过程中振动信号的刀具磨损特征的有效提取，从而对其进行准确识别。