基于BP神经网络的水电厂排水泵故障预警研究

唐孝舟，孙长兰，张玉彬，朱锦干，张军华

（南京南瑞继保电气有限公司，江苏南京 211102）

集水井是水电厂渗漏水、检修水和部分生产用水的排泄系统。电厂渗漏水和检修水通过管道或排水沟收集到集水井，待积累到一定数量后用水泵抽至下游［1－2］。若集水井排水不畅，轻则会水淹水泵，重则将可能导致水淹厂房。因此，集水井排水泵对于水电厂安全运行十分重要。随着运行时间的增长，加上长期泥水的冲击，排水泵可能会出现轴承磨损、性能下降的问题［3－4］。如何及时对排水泵故障进行预警，在故障发生之前就抢先发现并消除故障有着重要意义。随着技术的进步，当前水电厂集水井排水泵一般采用可编程逻辑控制器（Programmable Logic Controller，PLC）来实现自动控制，当水位超过设定值时自动启动，当水位下降至设定值时自动停止［5－6］。同时，集水井排水泵的运行数据也会通过PLC上送给电厂计算机监控系统。排水泵的启停时刻、排水时长也可以被计算机监控系统详细记录，为排水泵故障预警研究创造了有利条件。另一方面，机器学习算法日益普及，其中的BP神经网络被广泛用于各种科学研究和工程应用。本文通过构建一个BP神经网络来实现水电厂排水泵故障预警功能。

1 建 模

1.1 排水系统特性分析

水电厂集水井排水泵一般采用PLC自动控制，当水位超过设定值时自动启动，当水位下降至设定值时自动停止。如图1所示：H1是排水泵启动水位；H2是排水泵停止水位；横轴方向T1和T3是水泵启动时刻；T2和T4是水泵停止时刻。则排水泵在当前水位、当前时间范围内运行时间为T2－T1＋T4－T3。显然，这个时长取决于集水井水位以及排水泵的排水能力，并且水位是具体的已知的变量，排水能力是抽象的未知的变量。

水电厂计算机监控系统一般每个小时统计一次排水泵的运行时长（单位为s），以分钟为单位来采集集水井的水位（单位是m）。因此，上述问题转化为：在第i个小时内，输入是一个水位序列，从第0 min到第59 min共计60个数据组成的数组Hi＝［h0，h1，…，h59］，输出是排水泵运行时长，记为Ti，其单位是s，取值范围在0～3 600之间。如果通过m条历史数据来分析集水井水位与排水泵运行时长的关系，则此时输入为Tm×60，输出为Tm×1。

1.2 集水井来水量分析

排水泵启停次数、排水时长除了受集水井水位的直接影响以外，还会受来水量的间接影响。水电厂集水井一般分为渗漏集水井、防洪集水井、检修集水井，不同类型集水井来水量又受到不同因素的影响。渗漏集水井与水轮机阀门、主轴密封密切相关，防洪集水井来水量主要受到降雨量影响和水库水位的影响，检修集水井来水量则与检修工作密切相关。用type表示集水井类型，定义type＝0时表示渗漏集水井，type＝1时表示防洪集水井，type＝2时表示检修集水井。用ωi（type）来表示时段i的来水量影响因子，则其表达式为

式中：αi是一个水轮机阀门、主轴密封表征参数，因机组寿命、运行状况而异，根据水电厂运行经验取值，其取值区间为［0，1］；βi、γi分别为时段i的水库水位、降雨量，取实际测量值；δi在检修时取1，非检修时取0。

综合考虑集水井水位、来水量后，排水泵运行时长的自变量为［H60，ωi（type）］m×1，因变量为Tm×1。

1.3 BP神经网络选择

BP神经网络是一种最有效的多层神经网络，它包含输入层、隐含层、输出层［7－8］。其主要特点是信号前向传递，而误差后向传播，通过不断调节网络权重值，使得网络的最终输出与期望输出尽可能接近，以达到训练的目的［9－10］。图2为典型BP神经网络结构图，其中：第1层称为输入层，最后一层（第L层）被称为输出层，其他各层均被称为隐含层（第2层到第L－1层）。

令输入向量为X＝［x1，x2，…，xm］，输出向量为Y＝［y1，y2，…，yn］，隐含层神经元输出为hl＝［，，…，］，设为从l－1层第j个神经元与l层第i个神经元之间的连接权重；为第l层第i个神经元的偏置，那么权重和偏导的计算公式为

BP网络模型训练完毕之后，在进行预测的时候，只需要将输入量的实时采集数据送入BP网络，经前向传播，输出的结果即为预测数据。

BP神经网络的隐含层一般采用一层即可，层数过多反而不利于模型的训练和收敛。本文采用的即是这种结构，整个BP神经网络就由输入层、隐含层、输出层三层来构成，输入层为集水井水位和来水量矩阵X＝［H60，Wi（type）］，输出层为1 h内水泵的运行时长Y＝Ti（单位是s）。这种结构的BP模型具有训练简单、效率高的优点，便于现场应用。

1.4 数据预处理

神经网络是以样本在事件中的统计分布机率来进行训练和预测的，并且激活函数sigmoid的取值是0到1之间的［11－12］，网络最后一个节点的输出也是如此，所以经常要对样本的输入、输出做归一化处理。归一化是统一在［0，1］之间的统计概率分布，当所有样本的输入信号都为正值时，与第一隐含层神经元相连的权值只能同时增加或减小，从而导致学习速度很慢。另外在数据中常存在奇异样本数据，奇异样本数据存在所引起的网络训练时间增加，并可能引起网络无法收敛。为了避免出现这种情况及后面数据处理的方便，加快网络学习速度，可以对输入信号进行归一化，使得所有样本的输入信号其均值接近于0或与其均方差相比很小。归一化可以通过MinMaxScaler函数来实现，其公式为

式中：x为需要归一化的特征向量；xmax和xmin分别表示x中最大值和最小值；ymax和ymin分别表示对应数据归一化后，区间范围中的最大与最小数值。此时所有输入数据都被归一化到［0，1］区间。将Hm×60和Tm×1都按照此方法归一化，归一化之后的数组分别记为Xm×60和Ym×1。

1.5 模型训练

为了增强模型适应度、提高训练准确性，将m组数据集按照8∶2比例随机划分为训练集和测试集。具体方法是使用python程序中的scikit－learn模块自带的train＿test＿split函数。该函数在划分训练集和测试集时完全是随机的，可以减少偶然性误差。同时，由大数定理可知，试验次数越多，事件发生概率越趋于稳定。因此，将划分过程重复10次，形成10个数据集记录为DataSeti（i＝1，2，…，10），第i个数据集中的训练集记录为TrainDataSeti，测试集记录为TestDataSeti。

1.6 模型评估

针对BP神经网络模型，一般采用均方根误差（RMSE）、平均绝对误差（MAE）和决定系数R2来评价模型的好坏。其公式如下：

式中：m表示输出向量个数；yi表示实际值；y′i表示预测值。

为了获得准确的模型评估，运用循环算法对上面划分好的10组数据展开训练，训练的目的是确定激活函数和中间层网络的节点个数，同时获得不同条件下的评估指标。最后根据各项评估指标确定最好的BP神经网络模型。

2 实例分析

按照1.1、1.2节建模方法，从南方某省份一大型水电厂获取了防洪集水井6个月共4 320 h的水位、来水量数据，按照1.4节所讲方法进行数据预处理之后，共形成10个DataSet数据集，每个数据集包含数据4 320条，其中又进一步划分为训练集数据3 456条，测试集数据864条。接下来对10组不同的DataSeti数据集，按照不同条件展开实验分析。

2.1 激活函数选择

当神经网络激活函数分别设定为sigmoid和ReLU时，BP神经网络训练结果如表1所示。可以看到在相同情况下，sigmoid作为激活函数时，其均方根误差RMSE、平均绝对误差MAE大幅小于ReLU激活函数，而决定系数R2则远高于后者。因此激活函数设定为sigmoid能获得到较好的预测模型。

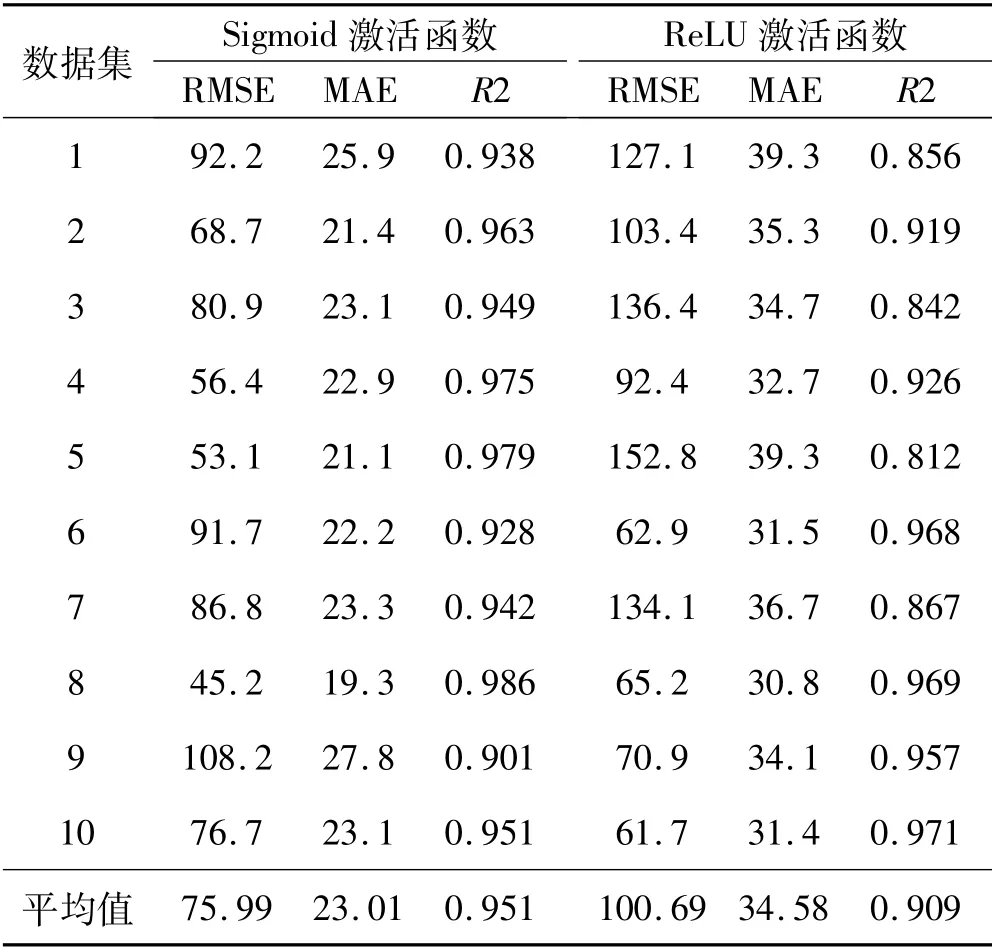
表1 不同激活函数预测结果对比

2.2 隐含层节点数设定

当激活函数设定为sigmoid后，改变隐含层节点数，重新进行模型训练，结果如表2所示。可以看出当隐含层节点数为60时，其均方根误差RMSE和MAE大于节点数为100的情况，但是其决定系数优于后者，当隐含层节点数为150时其各项指标都不如节点数为100，因此设定神经网络的隐含层节点数为100。

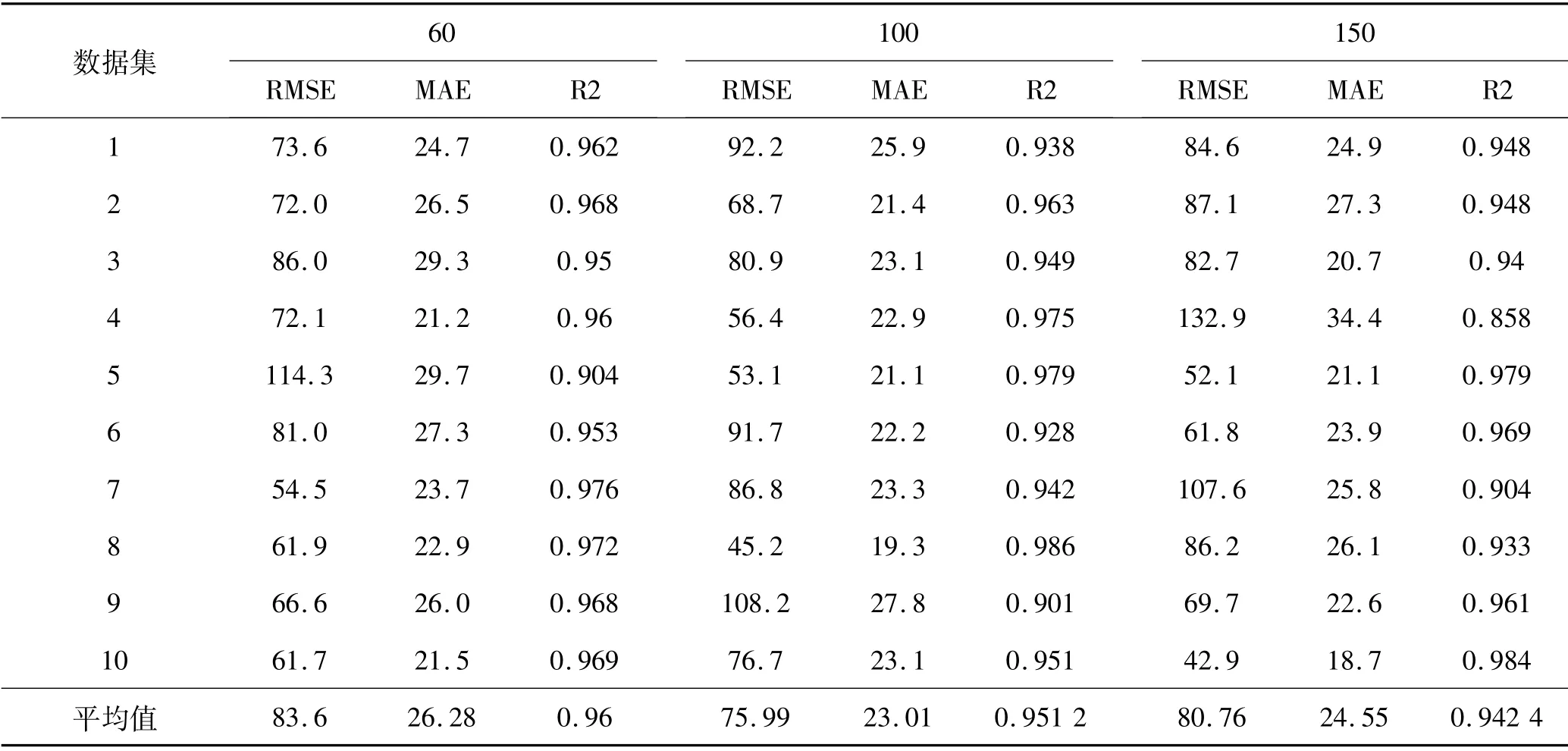
表2 不同隐含层节点预测结果对比

2.3 排水泵运行时长预测

根据前面的对比结果，BP神经网络隐含层节点数设置为100，激活函数设置为sigmoid能取得最好的模型，并且模型的均方根误差平均值RMSE＝75.99。模型训练好之后就可以按照小时为单位对排水泵的排水能力进行预测，然后跟实测值进行比较，观察预测效果。表3展示了连续12 h的排水泵运行时长预测结果。

统计学中经常使用拉依达准则（也称准则）用于剔除异常数据［13］，具体方法是将单一变量同一时刻的采集数据构造数组X，计算其标准偏差σ。取其中最大偏差值与3σ进行比较，若最大偏差大于3σ，则对应的测量值即为“粗大误差”，需要被剔除。而BP神经网络其本质也是用统计学方法进行训练和预测，因此3σ可以用于效果评估。BP神经网络模型的均方根误差RMSE就是标准偏差σ，3σ可以用3RMSE来代替。从表3数据可以看到，连续预测误差最大值刚刚接近RMSE，所有预测误差都没有超过3RMSE，不存在预测上的“粗大误差”，预测效果良好。

表3 水泵连续12 h运行时长预测结果对比s

2.4 故障预警策略

首先对排水泵的排水能力进行预测，然后跟实测值进行比较，采用某种判据就可以产生预警［14－15］。本文借鉴统计学中的3σ准则作为故障预警的判据。由前面的描述可知3σ可以用3RMSE来代替，因此预警策略可以设定为｜y－y′｜＞3RMSE，其中y是排水泵1 h内的实测运行时间，y′是通过BP神经网络预测的水泵运行时间。

根据前面的模型训练结果可知，本文选用的BP神经网络模型均方根误差RMSE＝75.99 s。预警策略可以简化为｜y－y′｜＞3×75.99≈228。即某个小时内排水泵实测排水时间与预测运行时间误差超过228 s时，即认为水泵存在排水异常的可能。实际现场应用时为了减少误报警的可能可以进一步增加裕度，即当误差超过了3RMSE，也可以暂时不给运行人员推送告警，而是认为此时刚刚达到预警启动条件，是否发出故障预警由下1 h的结果来决定。如果下1 h误差未超过3RMSE，则认为上一次启动为误报，将启动状态复归，否则立即向运行人员发送故障预警信号，提示运行人员对排水泵运行状态进行巡检。整个过程实现的伪码如下：

3 结 语

本文所提基于BP神经网络的水电厂排水泵故障预警方法，通过分析排水系统的历史运行数据，先后确立了激活函数、隐含层节点数等重要参数，从而建立了BP神经网络模型，再根据集水井水位、来水量情况预测排水泵的理论运行时间，将该数据与实测数据做比对，发现异常时及时给运行人员推送告警，从而安排检修。相比于传统的限值预警，本文采用基于机器学习的方法，在对历史数据充分学习的基础上，预警结果更能反映设备的实际运行状态。该系统目前已经在某大型水电厂计算机监控系统内试运行。从现场运行的情况来看，预测精度良好，为排水泵及早发现故障提供了一种新手段。由于本文故障判定采用的是固定阈值的方法，实际在现场运行过程中，随着排水泵老化，其排水能力会越来越差，如何动态的确定故障阈值将是一个值得研究的问题。