大气边界层高度的确定及其在数值天气预报模式中的应用

汪晋，廖前锋，闫申，王毅，项杰

(1.南京工业大学浦江学院，南京211222；2.陆军工程大学教务处，南京210007；3.国防科技大学前沿交叉学科学院，长沙410028；4.国防科技大学气象海洋学院，长沙410028)

引 言

大气边界层(Atmospheric Boundary Layer，ABL)位于对流层底部，是最接近地球表面的一层大气。由于受到地表摩擦和非绝热加热等的影响，ABL具有明显不同于其上自由大气的特征，如，有别于自由大气中的平流特征，ABL 内大气的运动形式主要为湍流，会对动量、热量和水汽等的输送过程产生重要影响(Stull，1988；赵鸣和苗曼倩，1992；Garratt，1992；盛裴轩等，2013)。研究ABL过程对了解大尺度天气过程的演变、研究长期预报和气候理论等问题，具有重要的意义(高登义，1994；周明煜等，2000；张强和胡隐樵，2001；胡非等，2003；Medeiros et al.，2005)。此外，人类主要生活于ABL 内，ABL 对人们的生产、生活等各种活动有重要影响。如ABL与空气污染密切相关(任桂萍等，2021)，ABL 中的湍流运动对于空气污染物具有扩散和混合的作用(因而在空气污染气象学中ABL又称为混合层)；ABL高度决定了污染物扩散稀释的潜在空间范围，ABL 高度高时，污染物可以在更大的空间内扩散稀释，从而降低浓度。因此，ABL 高度与近地面污染物浓度呈负相关(Du et al.，2013)，重污染过程往往伴随较低的ABL高度(Qu et al.，2017)；同时，作为空气污染物主要成分的气溶胶对ABL 也有反馈作用(Yu et al.，2002；Li et al.，2017)；对于都市ABL来说，高的颗粒物浓度会加强ABL的稳定性，这会进一步地降低ABL 的高度，导致颗粒物浓度进一步增加(Petaja et al.，2016)。所以，研究ABL 过程对于保护环境以及保障人民的身心健康具有重要的作用。

ABL 与降水(尤其是强降水，如暴雨)过程有密切的关系。研究表明，ABL 中的物理过程，如ABL 中的动量、热量、水汽的输送、ABL中的摩擦效应以及地形的作用等对于暴雨的发生发展有重要的影响(Benjamin and Carlson，1986；赵鸣，2008；陈鹏等，2014)。由于ABL中湍流运动的尺度很小(属于次网格尺度的运动)，大气数值天气(或气候)模式难以解析这种尺度的运动，通常需要进行参数化处理。因此，ABL 过程的参数化一直是数值天气预报模式及数值气候模式研发的关键问题之一，也是暴雨模拟研究中的热点问题(蔡芗宁等，2006；盛杰和林永辉，2010；沈新勇等，2017；程锐等，2019)。ABL高度(或深度)是ABL的一个重要参数，估计准确的ABL高度数值对于数值天气(或气候)模式具有重要的意义。一方面，ABL高度数值是ABL 本身的参数化方案所必须的；另一方面，它也是数值天气(或气候)模式中其他的物理过程参数化所需要的。同时，ABL高度信息也是空气污染物预报模式的输入参数。准确的ABL 高度数据对于提高数值天气预报精度、化学成分预报精度等有重要影响。因此，确定ABL高度在气象学上具有重要意义(潘云仙和蒋维楣，1982；洪钟祥等，1998；李茂善等，2006；伍大洲等，2006；张璐等，2011；孔扬和张苏平，2014)。

根据大气的层结稳定性ABL分为不稳定ABL、稳定ABL 和中性ABL。不稳定ABL 又称为对流ABL(Garratt，1992)，通常出现在地表受热产生对流或云顶辐射冷却产生对流的情形下，其顶部往往伴随着逆温和(或)湿度的急剧下降；稳定ABL通常在夜间出现，常常伴随着以地表为底的逆温层(Garratt，1992)；中性ABL 较少出现，如陆地夜间ABL 中的剩余层(Residual Layer，RL)就属于中性ABL(Stull，1988)。不稳定ABL的顶(其高度即为ABL高度)常常可以根据一些物理量在ABL顶具有显著的梯度(如逆温、水汽含量的急剧下降等)而确定，而稳定ABL 顶的确定却没有统一的标准。在实际应用中，稳定ABL顶可以根据需要采用不同的方式定义，如定义为以地表为底的逆温层的顶(Seidel et al.，2010)，或者是湍流强度占近地面湍流强度的一小部分比例的位置(Stull，1988)，或者是利用Richardson 数 定 义(Vogelezang and Holtslag，1996)。不 稳 定ABL 的高度从数百米到数千米不等，而由于稳定ABL中的湍流扩散弱，稳定ABL 的高度最多不超过几百米(Garratt，1994)。

确定ABL 高度的研究工作有很多。张宏昇等(2020)对ABL 高度的确定作了很好的总结，介绍了两种类型的确定ABL高度的研究工作，其一是利用遥感观测数据确定ABL高度，重点是地基遥感观测数据(如激光雷达/云高仪、地基微波辐射计、声雷达、风廓线雷达、多普勒测风激光雷达等数据)，对于卫星遥感数据只是简单介绍了掩星探测数据的应用；其二是利用预报方程、诊断公式通过参数化的方法计算ABL 高度，其优点是只需输入少量数据即可计算得出ABL高度，尽管方法简便实用，但所得结果精度相对较差，在缺乏大气廓线观测值的地区参数化方法有较高的应用价值。至于ABL高度数据的应用，该文献只在引言中笼统地提及了在天气预报和空气质量预报模式中有应用，并没有详细的研究工作介绍。本文从不同角度介绍了ABL高度的确定及其应用，即针对四种常见类型的观测资料，包括常规探空资料、卫星遥感探测资料、激光雷达探测资料及全球导航卫星系统GNSS(Global Navigation Satellite System)掩星探测资料，介绍确定ABL高度的主要方法及其进展情况；通过对不同方法和结果进行比较，提出在同时具有多种观测资料时如何处理ABL 高度的三个基本原则；最后，以目前广泛应用的数值天气预报模式WRF (Weather Research and Forecasting)为例，重点介绍ABL 高度数据在数值天气(或气候)预报模式中的应用，以期为改进、完善数值天气(或气候)预报模式中的ABL参数化方案提供有益的参考依据。

1 利用常规探空资料确定ABL高度

对于不稳定ABL来说，ABL顶往往伴随着一个或多个物理量存在明显的梯度，如温度(逆温)、湿度、气溶胶粒子浓度、臭氧浓度、湍流强度和折射率等。因此，利用这些物理量的单个探测廓线或模式输出廓线就可以确定ABL 顶所在的高度，即ABL高度。常规探空数据一直是气象学家确定ABL 高度的主要数据源(Seibert et al.，2000；徐桂荣等，2014；Dai et al.，2014)，基于常规探空廓线确定ABL 高度的方法主要包括气块法、最大梯度法、湍流法及Richardson 数法等四种，下面分别进行简要介绍。

1.1 气块法

Holzworth(1964)提出了“气块法”的基本思想，把从地面(具有最高温度的)某点出发的干绝热廓线与该处(或临近的)探空温度廓线的交点处的高度定义为ABL高度，即在这个高度上与在地面具有相同的虚位温值。利用该方法确定的ABL 高度也称为“混合高度”，通常用于空气污染物的预报以评估在ABL 中释放的污染物的浓度。然而用这种方法确定的结果强烈依赖于地面温度，会出现对流ABL顶没有逆温的情形(Seibert et al.，2000)。因此，Beljaars和Betts(1992)提出了改进的气块法，并且被Wotawa 等(1996)和Seibert等(2000)所应用。气块法是一种基本的方法，主要用于不稳定ABL的情形。

1.2 最大梯度法

ABL 顶往往伴随着逆温和(或)湿度等的急剧下降，通常利用位温最大垂直梯度来确定ABL 高度(Stull，1988；Garratt，1992)，这种位温最大垂直梯度层表示从对流不稳定区域(位于下方)到位于上方的稳定区域的过渡区。Ao等(2012)直接利用温度或湿度的最大垂直梯度(绝对值)确定ABL 高度，具体实施时需要首先计算位温(或温度、湿度)的垂直梯度，由于观测数据往往含有噪声，再加上算法的原因，计算得到的垂直梯度可能含有较大的误差，导致结果不可靠，甚至是错误的。针对这种实际情况，有学者在计算垂直梯度之前先对数据进行滤波等平滑处理(Amiridis et al.，2007；杨富燕等，2016)；Zeng 等(2004)在最大梯度法中采用了阈值判据，即对于海洋上的不稳定ABL，把虚位温的垂直梯度首次大于或等于3 K·km-1(称为阈值)所在的高度作为ABL高度；Dai等(2014)利用位温垂直梯度廓线来确定对流边界层(Convective Boundary Layer，CBL)或云盖顶边界层(Cloud-Topped Boundary Layer，CTBL)高度：对于CBL 来说，其顶部逆温层相对较弱，故设置相对较小的位温梯度阈值来确定ABL高度(即在逆温层底部首次超过阈值的高度)；而对于CTBL来说，其顶部逆温明显，故可以设置相对较大的位温梯度阈值来确定ABL高度，或者直接取位温梯度最大值所在的高度为ABL 高度。为了减少观测误差对计算梯度的影响，还可以采用数值微分方法(Cheng et al.，2003；Xiang et al.，2021)。

在最大梯度法中采用阈值判据时，阈值的选择具有一定的主观性，这会产生估计的ABL高度的不确定性。最大梯度法既可用于不稳定ABL 也可用于稳定ABL，但是对于稳定ABL，最大梯度法应用起来更复杂(Dai et al.，2014)。目前，最大梯度法仍然是确定ABL高度的主要方法，应用广泛。

1.3 湍流法

ABL 与自由大气之间的主要区别在于ABL 具有湍流性，湍流能够使ABL 内产生混合过程，因而ABL能够响应地表的强迫。因此，ABL可定义为湍流扰动层，而ABL 高度就为湍流消失的高度，也即存在连续湍流的最大高度(Dai et al.，2011)。探测ABL 高度的湍流方法就是利用仪器(如放置于飞机上)直接(高频)观测垂直风速，得到垂直风速廓线，然后对风速廓线进行高通滤波(如小波滤波器)，消除低频分量，得到风速脉动值，风速脉动值显著减少的高度就是ABL 高 度。Wang 等(1999)、Dai 等(2011)、Zhang 等(2014)均利用了湍流方法对外场观测数据确定了ABL高度。

湍流方法被认为是确定ABL 高度的最准确的方法，对任何类型的大气层结(不稳定、稳定、中性)都适用。但是，湍流直接观测中所使用的设备代价昂贵，所以除了在科学实验中偶尔使用以外，日常观测很少使用这种设备，这决定了湍流方法在确定ABL高度的工作中应用较少。

1.4 Richardson数法

Richardson 数是一个无量纲数，表示浮力抑制的湍流与风切变产生的湍流之比，是判定湍流产生与否的重要参数，也是判定流体静力稳定性的指标，可直接用来估算ABL 高度，这就是确定ABL 高度的Richardson数法。

Richardson 数法既可应用于不稳定ABL，也可应用于稳定ABL(Georgoulias et al.，2009)，特别适合于在数值天气预报模式中确定ABL 高度(Straume et al.1998；Zilitinkevich and Baklanov，2002；Jericevic and Grisogono，2006)，因为数值模式中需要进行自动处理。Richardson数法也可应用于从探空资料确定ABL高度(Zeng et al.，2004；Balsley et al.，2006；Hennemuth and Lammert，2006；Sicard et al.，2006)。如Guo 等(2019)利用中国区域1976—2016 年的无线电探空资料，采用整体Richardson数法确定了ABL高度，并分析了ABL高度的时空变化特征。

Richardson 数法建立在这样一个基本假设之上，即当Richardson 数超过某个临界值时连续湍流会终止。这种方法的一个弊端是它的临界值选取的不确定性，临界值选取可从0.15变化至0.55，而且一旦选定以后，这个临界值对于所有类型的ABL(不管是不稳定的、稳定的还是中性的)都是相同的，这不太合理；同时，Richardson 数法并不太适用于大多数被动的空基反演的温度廓线(红外和微波)，因为被动获取的廓线的垂直分辨率最多为1～2 km，对于估计ABL 高度，这是一种非常粗略的分辨率。为了弥补Richardson数法的不足，Zhang等(2014)利用四个外场观测实验的数据对Richardson 数法的临界值进行了修正，把四个外场实验中观测到的ABL分为强稳定ABL、弱稳定ABL和不稳定ABL三类，对每一类都利用线性拟合和统计误差最小化方法得到各自最优的Richardson 数临界值。这样，对不同稳定性的ABL采用不同的临界值就可以得到更准确的ABL 高度估计值。Zhang 等(2014)的Richardson数临界值选择方案值得进一步发展应用。

2 利用常规卫星遥感资料确定ABL高度

利用卫星遥感资料确定ABL 高度的优势在于可得到其时空变化的全球和区域统计特征，许多研究在这方面提出了不同的方法和技巧。Minnis 等(1992)、Wood 和Bretherton (2004)、Zuidema 等(2009)先后利用副热带海洋上空层云和层积云顶的温度和海表温度(sea surface temperature，SST)来估计ABL 高度，其原理如下：ABL内的温度廓线与干绝热廓线很接近，并且在大多数海洋上海气交界面处的海气温度差异是很小的，因此可以使用海表温度SST结合干绝热大气的温度直减率得到ABL高度。从气候学研究的实用性角度考虑，这个方法只适用于完整云块的区域，对于陆地或深度浅的积云区域效果并不好。因此，有人提出了直接利用云顶高度估计的改进方法，Wu 等(2008)使用空基激光雷达估计云顶高度来确定ABL 高度，而Karlsson等(2010)利用多角度成像光谱辐射计估计云顶高度来确定ABL高度。但是，以上这些方法都面临着同样的问题，即块状云的顶并不总是与ABL顶一致。

另一些研究人员则直接利用卫星遥感反演的温湿廓线数据确定ABL 高度。Fetzer 等(2004)利用大气红外探测仪AIRS反演的温度和湿度廓线资料来确定位于ABL顶的逆温位置，因而得到ABL高度。该方法的不足之处是，它仅能给出ABL高度的粗略估计，因为廓线的垂直分辨率是很低的(对温度来说是约1 km，对湿度来说是约2 km)，不足以解析ABL顶的细微结构。

因此，利用常规卫星遥感资料确定ABL高度还存在明显的不足，这方面的研究工作相对较少。

3 利用激光雷达探测资料确定ABL高度

激光雷达的主要探测数据为后向散射回波信号强度，它受气溶胶和水汽的影响大。许多影响光散射的气溶胶粒子来自于地球表面(如海盐、灰尘和土壤颗粒)，因为ABL 顶通常具有逆温特性(属于稳定层结)，这限制了这些气溶胶粒子向上的扩散，因此气溶胶粒子主要分布于ABL内，在ABL和其上的清洁大气之间气溶胶粒子浓度有一个显著的下降，反映在激光雷达回波信号中，就是后向散射回波信号强度在ABL顶也有 一 个 显 著 的 下 降(Boers et al.，1984；Hooper and Eloranta，1986)，这 一 特 征 可 用 来 确 定ABL 高 度。Hooper 和Eloranta(1986)利用地基激光雷达探测ABL风速时也探测了ABL 深度(即ABL 高度)，提出了确定ABL深度的后向散射方差法(backscatter variance，也称为标准差法)。Steyn等(1999)、Hageli等(2000)、Eresmaa等(2012)提出了曲线拟合方法，用理想的激光雷达后向散射强度廓线拟合实际的后向散射观测数据来确定混合层深度和(或)夹卷层厚度。Davis 等(2000)、Brooks(2003)提出利用小波协方差变换方法确定ABL高度。Sawyer 和Li (2013)、Hicks 等(2015)还将曲线拟合方法和小波协方差变换方法结合起来确定ABL 高度。这些方法本质上都是最大梯度方法。由于激光雷达具有高时空分辨率和较高精度的优势，利用激光雷达探测ABL高度近年来受到了广泛的重视(Wang et al.，2012；王琳等，2012；Compton et al.，2013；李红等，2015；Lewis et al.，2013；杨富燕等，2016)，它既可以用来探测陆地ABL 高度(McGrath-Spangler and Denning，2012)，也可以用来探测海洋ABL 高度(Palm，2005)，还可以探测全球ABL高度，如星载激光雷达(Zhang et al.，2016)，稳定与不稳定ABL 都可以探测，是一个前沿的研究方向。

4 利用GNSS掩星探测资料确定ABL高度

作为一种新型的大气遥感探测手段，GNSS 掩星探测技术具有高精度、高垂直分辨率、全球准均匀覆盖、全天候观测、长期稳定等特点(Kursinski et al.，1996；Kuo et al.，2004)，在国际上受到广泛的重视。一些国家启动了众多的掩星探测项目，这些项目获得了大量的中性大气和电离层电子密度廓线数据，这些数据在数值天气预报、气候及空间天气研究和预报等方面得到了广泛的应用。如我国台湾地区与美国联合实施的掩星探测项目“气象、电离层和气候星座观测系统(Constellation Observing System for Meteorology，Ionosphere and Climate，COSMIC，2006-2011)”成为最成功的掩星探测业务应用系统。在COSMIC 项目之后，美国和台湾地区又推出了名为FORMOSAT-7/COSMIC-2的后续掩星探测项目，COSMIC-2项目每天能跟踪超过4 000多条高质量廓线。

由于GNSS 掩星探测技术具有独特的优点，特别适合于气候学研究，因此不少学者利用掩星探测数据产品来确定ABL 高度。von Engeln 等(2005)利用全谱反演中的截断高度来确定ABL 高度；Sokolovskiy 等(2006)利用线性回归方法估计折射率廓线的垂直导数，通过确定折射率垂直梯度的最大下降点(断点，即不连续点)来确定ABL 高度；Sokolovskiy 等(2007)又提出利用弯角廓线确定ABL高度，其思想是确定固定长度范围(一般取300 m)内的弯角最大下降值。Guo 等(2011)采用断点方法，利用一年的COSMIC掩星探测折射率数据得到了热带和亚热带海洋地区ABL 高度的时空分布，并且空间分布特征与欧洲中期天气预报中心ECMWF(European Center for Medium-Range Weather Forecasts)全球分析资料的结果一致，但是平均来说前者的量值要大于后者的量值。Ao等(2012)把折射率和水汽压垂直梯度的最小值点看作为ABL顶，其高度定义为ABL高度，并且引入了相对最小梯度(或显著参数)来表征所得ABL 高度的质量指标，结果表明由COSMIC 掩星数据确定的ABL 高度的平均值与ECMWF 再分析资料(European Center for Medium-Range Weather Forecasts reanalysis interim，ERA-Int)的结果具有相似的空间分布和季节变化特征，但是前者比后者要高500 m，且COSMIC 掩星数据的ABL 高度的标准差也高于ERA-Int的相应结果。其他一些学者也进行 了 类 似 的 工 作(Chan and Wood，2013；Ho et al.，2015；廖麒翔等，2015；刘艳等，2015)。Basha 等(2018)利用小波协方差变换方法基于全球多个掩星探测计划数据得到了全球ABL高度的气候态分布，这些分布显示了ABL 高度具有明显的季节变化，其中夏季最高，春秋次之，冬季最低。周文等(2018)利用COSMIC掩星资料，通过计算大气折射率最小梯度来确定青藏高原地区ABL高度，并用无线电探空资料对结果进行了检验。而Yan 等(2019)、周建印等(2020)、Xiang 等(2021)则利用数值微分方法结合反问题中的正则化策略来计算弯角、折射率廓线的垂直梯度进而确定ABL高度，该方法在理论上更严谨，适用范围更广。

利用GNSS掩星探测资料确定ABL高度的不足之处有：掩星探测未必能达到地表附近，因此对于浅薄的ABL(尤其是稳定ABL)，掩星探测技术不太容易探测到它们的高度。

5 确定ABL高度的不同方法和结果的比较

上文介绍了用于确定ABL 高度的各种数据及主要方法。一些学者对不同方法及不同数据的结果进行了比较研究。如Seidel等(2010)利用全球10 a的505个探空站的观测资料(包括正常分辨率和高分辨率的廓线数据)，对七种方法(气块法、位温的最大垂直梯度法、比湿的最小垂直梯度法、相对湿度的最小垂直梯度法、折射率的最小垂直梯度法、悬空的逆温层法、以地面为底的逆温层法即稳定ABL法)确定ABL高度进行了对比分析，探讨了ABL高度气候态数据中的参数不确定性(指温度、位温、虚位温、相对湿度、比湿、折射率数据所得结果的差异)和结构不确定性(指所用的方法和数据分辨率的不同而产生的差异性)，得到了一些有意义的结果。例如，不同方法所得结果的差异达到了数百米，ABL 高度对探空数据的分辨率更敏感，标准分辨率数据的结果比高分辨率数据的结果偏大等等。Gu等(2021)用11 a的COSMIC全球无线电掩星数据(小波协方差变换法)、无线电探空数据(Integrated Global Radiosonde Archive，IGRA) (整体Richardson 数法)以及欧洲中心再分析资料ERA-Int(气块法)对全球ABL高度进行了估算比较，结果表明ERA-Int和IGRA数据估算得到的全球ABL高度的空间分布较为一致，相关性较好；由COSMIC 掩星数据估算得到的ABL 高度比探空数据和再分析数据估算的结果系统性地偏大。

总之，用于确定ABL 高度的各种数据、各种方法都有各自的适应性和优缺点，利用不同方法、不同数据所得到的ABL高度具有差异性(不确定性)。如果同时利用多种观测手段获得了多种观测资料，如湿度、温度、臭氧浓度、湍流强度、示踪物(如气溶胶粒子)、折射率等，那么可以利用这些资料得到多个ABL高度的估计值，而且一般来说，这些估计值都是不相同的。如何处理ABL高度同时具有多个估计值的情形，是一个在实际应用中必须要考虑的问题。可以按照以下三个原则来处理ABL 高度具有多个估计值的“窘境”：(1)准确性原则。观测资料的准确性是其被采用的主要原则。如湍流法被认为是确定ABL 高度的最准确的方法，如果有湍流强度的观测资料，则应该首先利用湍流强度观测资料确定ABL 高度；又如，卫星遥感反演的温度相对湿度来说准确性更高，因此在没有湍流强度观测资料的情况下可以利用卫星遥感反演的温度廓线信息估计ABL 高度。如果有无线电探空的温度湿度廓线，由于探空的温湿廓线比卫星遥感反演的温湿廓线精度高，则可以利用探空的温湿廓线确定ABL高度。(2)目的性原则。根据研究任务目的的不同而选择合适的观测资料来确定ABL 高度。如在空气质量的模拟与预报中，可以采用气块法确定ABL 高度；而在ABL 高度的气候学研究中，可以利用GNSS 掩星探测折射率廓线数据来确定ABL 高度，因为折射率同时含有温度和水汽的信息，而且GNSS 掩星探测廓线数据具有高精度、高垂直分辨率、全球准均匀覆盖等优点，特别适合于气候学研究。(3)科学性原则。从科学上探讨ABL 高度出现多个估计值的原因。

6 ABL高度信息在数值天气预报模式中的应用

如前所述，数值天气预报模式都包括ABL 过程。ABL 过程的湍流特性决定了ABL 运动方程组的闭合主要采用参数化(即次网格尺度的湍流通量利用预报的平均变量通过垂直扩散方程来表示)来实现。参数化可以分为不同的形式，如1 阶闭合(利用K-理论)、1.5阶闭合(闭合后的方程中不仅包括1阶闭合情形的标准变量，还包括湍流的位温方差和湍动能)、2 阶闭合(闭合后的方程中只含有湍流的2阶矩量)等，也可以分为局地闭合和非局地闭合(根据参数化关系式是否仅使用局地的信息确定)。目前广泛应用的数值天气预报模式WRF 包含有多种ABL 参数化方案(Shin and Hong，2011)。常用的有：局地闭合方案，包括MYJ(Mellor-Yamada-Janjic)，QNSE (quasi-normal scale elimination)，Boulac (Bougeault-LaCarrere)，等 等(为1.5 阶 闭合)；非局地闭合方案，包括YSU (Yonsei University)，ACM2 (new version of the asymmetric convective model(ACM))，等等(为1阶闭合)。ABL高度信息在数值天气预报模式中的作用主要体现在：在ABL过程的参数化方案中，它是大多数参数化方案所必须的参量。

例如，在YSU 参数化方案中(Hong et al.，2006)，湍流运动的1阶非局地闭合产生如下的扩散方程

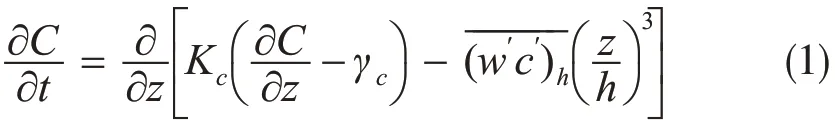
其中，C是预报变量，C=u，v，θ，q，qθ，qi，Kc是涡旋扩散系数，γc是对局地梯度的修正项(它代表大尺度涡旋对扩散的贡献)，是ABL顶逆温层的通量，h是ABL 高度，z是垂直坐标(从地面开始的高度)。动量涡旋扩散系数Km(C=u，v时的Kc)取如下形式(Hong et al.，2006)

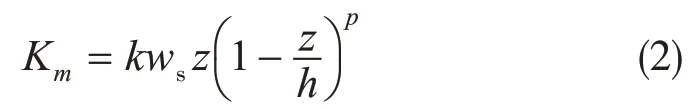
其中，p是廓线形状指数(通常取p=2)，k是冯卡门常数(k=0.4)，ws是混合层速度尺度，h、z的意义同上。

非局地扩散方程(1)的求解需要事先给定Kc的值，因此需要确定ABL高度h的数值。在YSU参数化方案中，h的值根据最低模式层和其上面的层之间的整体理Richardson 确定为第一个中性层的高度，具体来说是求解下列方程确定的

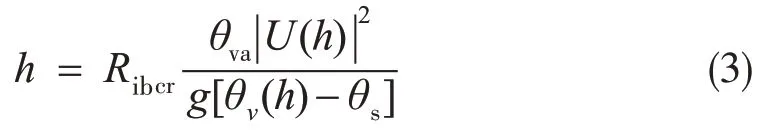
其中，Ribcr是临界整体Richardson 数(取Ribcr=0.5)，U(h)是高度h处的水平风速，θva和θv(h)分别是最低模式层和高度h处的虚位温，θs是地表附近的合适的温度值。

在ACM2 参数化方案中，同样需要确定ABL 高度的数值，其方法与YSU的类似。在MYJ、QNSE、Boulac参数化方案中，ABL高度h的值确定为湍动能TKE达到一个充分小的值(在WRF模式中，这个值取为0.005 m2·s-2)的高度。

对于不同的ABL过程参数化方案，其ABL内的混合方式、夹卷方式以及ABL高度的确定方式等都不一定相同，因此一些学者对ABL参数化方案的性能进行了评估研究。Hong 和Pan(1996)研究表明，中尺度数值天气预报模式在预报降水时，预报能力与非局地的垂直混合方案和临界Richardson数密切相关；Wisse和Vila-Guerau(2004)指出，在降水模拟过程中不同ABL参数化方案产生的模拟结果各有特点，并且对流性降水模拟结果对ABL 参数化方案十分敏感。Shin 和Hong (2011)通过利用WRF 模式对CASES-99 (the Cooperative Atmosphere-Surface Exchange Study)外场观测实验中的某一天的天气状态进行数值模拟，检验了上述五个ABL 参数化方案的性能。他们除了比较不同的ABL参数化方案对ABL结构的影响之外，还比较了参数化方案对ABL 高度的影响，结果表明，无论白天还是晚上，不同参数化方案所得到的ABL高度的差别都很大，QNSE参数化方案给出的ABL最深，而Bou-Lac给出的ABL最浅。Weisman等(2008)、Xie等(2012)的工作表明，局地闭合的ABL参数化方案诊断的ABL高度比非局地闭合的方案诊断的ABL高度要低。

LeMone等(2013，2014)专门利用ABL高度信息来评估ABL 参数化方案的性能，其利用CASES-97 (the April-May 1997 Kansas-based Cooperative Atmosphere-Surface Exchange Study) 外场观测实验期间获得的白天和夜晚的观测数据首先确定ABL高度(作为观测的ABL 高度)，然后利用这些ABL 高度值检验WRF 模式中的四种ABL 参数化方案(YSU、MYJ、Bou-Lac、QNSE)对观测的ABL高度的模拟能力。对于白天的对流ABL，LeMone等(2013，2014)直接把模式模拟的ABL 高度(即参数化方案给出的ABL 高度)与观测的ABL 高度进行比较，结果表明BouLac、MYJ、QNSE 参数化方案所得到的ABL 高度通常低于观测值，而YSU参数化方案得到的ABL 高度略高于观测值；对于夜晚的稳定ABL，未直接比较模式模拟的ABL 高度和观测的ABL 高度的偏差，而是比较它们在整个夜间的变化趋势，结果表明YSU和MYJ对于稳定ABL的高度模拟具有较高的准确度，而BouLac和QNSE的模拟能力则较差，需要进行改进。

可见，ABL高度信息不仅在ABL参数化中是必不可少的参量，同时也可用来检验ABL参数化方案的性能。由于不同的参数化方案各有优缺点，因此如何进一步改进完善现有ABL参数化方案仍然是一个挑战。

7 结论与讨论

本文从不同角度介绍ABL高度的确定及其应用，提出在同时具有多种观测资料时如何处理ABL 高度的三个基本原则，并WRF 模式为例重点介绍ABL 高度数据在数值天气(或气候)预报模式中的应用，主要结论如下：

(1)ABL是自由大气与地球表面(陆地和海洋)的连接通道，承担着两者之间动量、热量、水汽和气溶胶(污染物)等化学成分的交换任务，在地球气候系统中具有关键的作用。ABL高度是ABL的一个重要参数，数值天气(或气候)模式中的ABL过程的参数化均需要用到它，低层云的范围、种类及其演化与ABL 高度也有关系，准确获取ABL高度数据具有重要的意义。

(2)对估计ABL 高度的主要方法及进展情况进行了简要介绍。确定ABL高度的方法包括气块法、最大梯度法、湍流法、Richardson 数法等，这些方法本质上都是最大梯度方法，涉及到的数据主要有常规探空温湿廓线数据、卫星遥感反演温湿廓线数据、气溶胶浓度廓线数据、GNSS 掩星探测廓线数据等。关于ABL高度的研究，研究工作主要集中在两方面：一是从观测数据出发估计ABL高度并进行精度验证；另一方面是结合ABL参数化方案应用于数值天气(或气候)模式中，检验ABL 参数化方案对暴雨、台风等高影响天气过程模拟的影响以及数值模式对ABL 高度的诊断能力，以评估完善数值天气(或气候)模式和ABL 参数化方案。

影响ABL高度时空分布的主要因素有两个：湍流运动和垂直运动(Medeiros et al.，2005；韩美等，2012)；湍流运动与动力作用、热力作用及云顶辐射冷却有关，而垂直运动则与天气系统或大尺度背景环流有关。影响ABL 高度量值大小及时空分布的具体因素包括：大气稳定度、下垫面状况、太阳辐射、气溶胶粒子浓度、积云和层积云、大尺度天气系统等等(廖国莲，2005)。由于ABL 高度涉及的因素多、问题复杂，关于ABL 高度确定及相关的问题仍然是一个前沿性的问题。近年来随着人工智能技术的发展，机器学习技术广泛应用于各个领域，机器学习技术为人们研究ABL问题提供了新的手段和途径(Rieutord et al.，2021；Krishnamurthy et al.，2021)，有望解决ABL相关科学问题。

致谢：陈飞教授对ABL 高度数据在WRF 模式中的应用提供了指导，谨致谢忱！