图像化数据驱动的电力系统暂态稳定性在线评估方法

彭 鑫，刘 俊，刘嘉诚，李雨婷，刘晓明，赵 誉

（西安交通大学电气工程学院，陕西西安 710049）

0 引言

近年来，随着源-网-荷的大规模快速增长、波动性新能源以及跨区直流的快速发展等，现代电力系统的网架结构与运行方式千变万化，电力系统暂态稳定性分析中将面临更多未知的运行场景，对暂态稳定性在线评估的要求日益提高[1-2]。目前有3种常用的电力系统暂稳评估（Transability Stability Assessment，TSA）方法，分别是时域仿真法、直接法和人工智能方法。

时域仿真法精确度较高且数学模型详尽，然而工作量过大，计算速度慢[3]；直接法计算效率高，但依赖于非线性系统稳定性分析理论，目前仍未有重大突破[4]。随着人工智能的发展，机器学习方法在电力系统暂稳评估中的应用愈加广泛，通过对系统大量的暂稳样本进行离线训练，建立学习机模型和样本集的等价映射关系，将得到的模型用于暂态稳定性的离线/在线评估。目前常用于暂稳评估的机器学习方法主要有：决策树（Decision Tree，DT），深度置信网络（Deep Belief Network，DBN）和支持向量机（Support Vector Machine，SVM）等[5-13]，其中深度学习凭借其强大的学习能力在各方面都展现出了诸多优势，逐渐成为目前TSA 主流的方法之一[14]。

然而在实际电网中，由于母线、发电机、负荷等元件众多，导致输入矩阵的维度巨大，这将严重影响后续深度学习模型训练和预测的快速进行，难以实现在线监测。以某次中国西北五省电网的仿真实验为例，在某个运行方式下该区域共有11 059条母线、1 929 台发电机、5 633 条交流线联网。若单个样本选择全部母线和发电机在故障前、中、后共400 ms 的数据量作为输入，最终整理得到16 846×40 维矩阵，单个样本合计673 840 个元素。对于这样的高维矩阵，模型的训练和更新难以满足在线化的需求。虽然有部分研究涉及到特征的筛选或降维[15-18]，但这些方法往往只选取了电网中部分元件的电气量作为输入特征，必定会遗漏某些关键信息[19]。

本文提出了一种图像化数据驱动的电力系统暂态稳定性在线评估方法，相比于文本，图像能够存储更多的信息，再结合适当的图像特征提取与表达方法，能够有效融合不同类型的电气信息，从而在准确率和在线化目标上取得更大的优势[20-22]。本文所提方法的流程为：先将输入的样本重排为时间序列并转换为二维图像的形式，利用二维主成分分析（Two-Dimensional Principal Component Analysis，2D-PCA）变换对图像进行特征降维，再基于深度学习算法CNN 建立TSA 预测模型，并提出模型的在线更新策略，最终实现在线监视和预测，为基于人工智能的电力系统功角暂态稳定评估提供了一条新的思路。

1 2D-PCA与CNN原理

1.1 2D-PCA原理

2D-PCA 最早由Jian Yang，D.Zhang 等人于2004 年提出，主要用于图像识别等领域[23]。与传统主成分分析（Principal Component Analysis，PCA）不同，2D-PCA 在特征提取前不需要将图像矩阵转换为一维矢量，而是直接利用原始图像构造图像协方差矩阵，并导出其特征向量用于图像特征提取。与PCA 相比，2D-PCA 能够更好地保留图像的原始信息，还能大大缩减计算特征向量所需的时间，在识别精度和速度上都有很大优势。

2D-PCA 目标是通过线性映射变换Y=Xw将m×n的输入图像X投影到n维单位列向量w上，得到的m维列向量Y称为图像X的投影特征向量。数学上可以证明[22]，最佳的投影向量w满足如下条件：

式中：χ为n维单位列向量组成的向量空间；G为所有图像的协方差矩阵，是一个n×n的非负定矩阵。

设输入图像的样本空间由M个图像X1,X2…XM构成，所有样本的均值图像为，则G的表达式为：

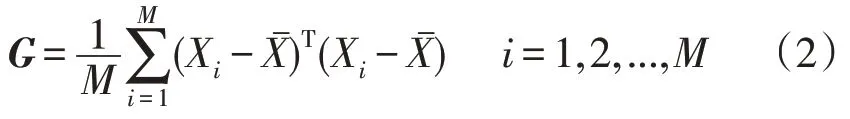
一般来说，只有一个最优投影轴是不够的，通常需要选择一组投影轴w1,w2,...,wd，服从标准正交约束和最大化准则，即：

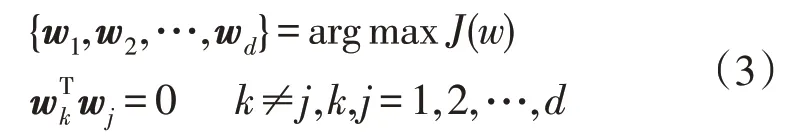
式中：为列向量wk的转置；wi(i=1,2…d)为协方差矩阵G的前d个最大的特征值对应的特征向量。

由PCA 相关理论可知，能够最大化J(w)的n维单位列向量由协方差矩阵G的前d个最大的特征值对应的特征向量构成。由这些列向量横向排列构成n×d维矩阵W，即为投影矩阵：

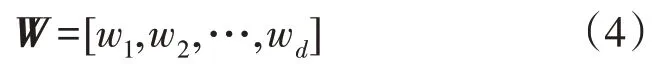
经过映射变换Y=XW得到m×d维矩阵Y，即为图像X的主成分，称之为X的特征矩阵或者特征图像。

1.2 CNN原理

卷积神经网络（Convolutional Neural Network，CNN）是深度学习的代表性算法，最早于1987 年由Alexander Waibel 提出，其特点在于通过共享权值的卷积核激励得到每一层的特征值。因此，CNN 相比于其他神经网络方法更适合应用于图像特征的学习与表达[24]。

CNN 一般由输入层、卷积层、池化层、全连接层和输出层组成，其基本结构见图1。

图1 CNN示意图Fig.1 Diagram of CNN

设CNN 的输入为原始图像X，第i层的特征图为Hi（k）。假设第i层为卷积层Hi，则其产生过程为：

式中：f(x)为激励函数；Wi为第i层卷积核的权值向量；bi为偏移向量；⊗为卷积运算符。

池化层通常在卷积层之后，用于对得到的特征图进行池化处理，其功能主要是降维和保持特征的尺度不变性。设第i+1层为池化层Hi+1：

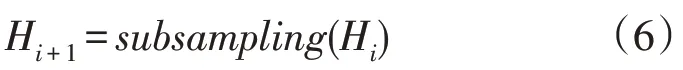
式中：subsampling()为池化函数。

在多个卷积层和池化层的交替传递后，添加全连接层对提取的特征进行分类，最终CNN 得到概率分布Y，根据该分布实现分类的目的。

2 基于2D-PCA和CNN的TSA方案

在TSA 中，由于输入特征主要是随时间变化的电气量，本质上就是多个时间序列的组合，具有明显的二维性。因此可以将输入时间序列重新排列为二维图像，这样做的目的主要有：

1）图像能够更加直观高效地存储系统的电气信息，在一定程度上还能促进信息间特征融合。

2）方便后续2D-PCA 直接处理原始图像，保留全维电气信息的同时实现特征降维。

3）降维后的特征图像能够直接作为CNN 的输入信息，而CNN 中卷积核能够有效融合不同电气特征。

实际上，在获取输入的时间序列并归一化之后，根据某个样本输入矩阵元素数值大小的不同，赋予相应的灰度值，可以绘制出该样本的图像，称之为原始图像，以某次实验得到的图像为例，如图2和图3 所示。

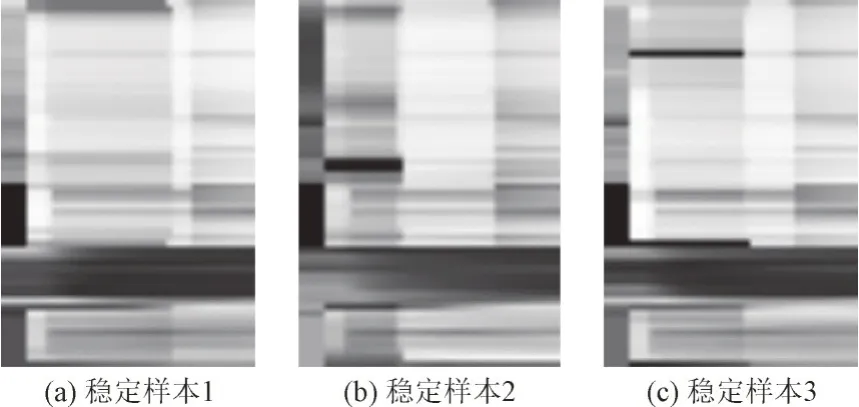
图2 3个稳定样本的原始图像Fig.2 Original image of three stable samples

图3 3个失稳样本的原始图像Fig.3 Original image of three unstable samples

可见，稳定样本和失稳样本之间的差距很明显，不同类型的样本在不同区域的明暗程度不同，大体上失稳样本比稳定样本亮度更低，因此看起来更暗。可见，将输入样本图像化不仅能够更加直观地体现不同类型样本之间的区别，还能方便后续模型的特征降维和提取过程。

本文所提基于2D-PCA 和CNN 的TSA 方案流程见图4。

图4 TSA流程图Fig.4 Flow chart of TSA

基于2D-PCA 和CNN 的TSA 方案包括离线训练和在线更新两个部分。

2.1 离线训练

首先通过时域仿真生成初始训练集D(Xi,yi)：

式中：M为样本总数量；F为特征总数量；T为时间节点总数量；(k=1,2,...,F,j=1,2,...,T)为第i个样本的第k个特征在第j个时间节点的物理量取值；yi为第i个样本的暂态稳定状态，取值为0 表示稳定，1 表示失稳。

先对所有样本进行标准化处理，防止因为不同特征的数量级差异影响后续特征降维和提取的效果：

式中：μ为x的均值；σ为x的标准差。

对标准化处理后的样本进行2D-PCA 降维：

式中：W为D(Xi,yi)的投影矩阵，其计算方法参照1.1 节。

得到降维后的特征矩阵X′，作为后续CNN 模型的输入量，建立CNN 模型的步骤如下：

1）向输入层输入特征矩阵X′，后接卷积层C1。

2）卷积层C1采用3×3 大小、总数为32 个的卷积核分别对输入层的图像进行卷积运算，得到特征图输出到下一层。

3）池化层P1大小为2×2，池化方式为最大池化，经过池化处理后得到特征图输出到下一层。

4）后续的卷积层C2、池化层P2操作步骤与步骤2）、3）相同。

5）全连接层FL对P2输出的特征图进行展开处理，得到一维的特征向量V。

6）以全连接层向后依次搭建3 层神经网络（Neural Network，NN），每层神经元个数分别为64，128，32。最终输入至判别层，输出稳定判别结果。

2.2 在线更新

由于在实际电力系统暂稳评估应用中存在大量的未知场景，不断会有新样本的加入，过去原样本集下的学习机模型通常不能准确评估未来可能出现的新场景。为了解决这个问题，需要对模型进行在线更新。

在本文所提的基于2D-PCA 和CNN 的TSA 模型在线更新中，包括投影矩阵更新和CNN 模型更新两部分。理论上，每当有新样本输入时，样本集都会发生改变，导致样本集的协方差矩阵改变，因此投影矩阵也会发生变化。但是若每个样本输入都更新投影矩阵，将会极大增加计算量，因此需要选择合适的样本更新单位K，当新增加K个样本后，更新一次投影矩阵。

此外，随着样本数量的不断增加，样本空间不断扩大，此时如果不对样本数量进行限制，将会急剧增加投影矩阵的计算量；同时，过早的样本也会影响模型对新样本的判断能力，此时剔除这类样本反而会提高模型的精度。因此需要选择合适的样本最大数量N，保证对新样本的预测精度，同时防止样本空间过大。本文采用的在线更新策略如图5所示，图5 中AC为新增样本的测试精度，ACset为设置精度最低期望值。

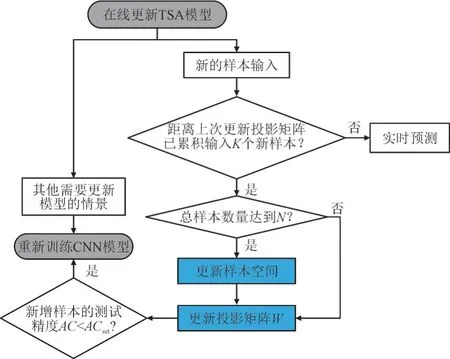
图5 在线更新策略Fig.5 Online update strategy

由于CNN 模型的每次更新都需要重新对样本空间的样本进行训练，非常耗费人力物力。当检测到最近新增加的K个样本的测试精度低于ACset时，对CNN 进行重新训练，更新一次模型；此外，当过久未更新模型或者其他需要重新训练模型的情景发生时，也会更新一次TSA 模型。

3 算例分析

本文所采用的算例为如图6 所示的IEEE-39节点系统，对故障后电力系统的暂态稳定性评估进行测试验证。该系统共有10 台发电机、39 个节点和46 条线路，其中节点2 为平衡节点，10 台发电机G 均采用双轴模型，励磁机采用IEEE DC Exciter Type 1 模型，19 个负荷均采用恒阻抗模型。

滑动t检验方法是通过考察两组样本平均值的差异是否显著来检验要素序列是否存在突变点（张庆广等，2012）。对已知的样本序列x1, x2……xn，定某一年份，分别取其前和后相邻的连续 n1和 n2的年平均值计算统计量T值，其中通过显著性检验的最大T值对应的年份即为突变年份。

图6 IEEE-39节点标准测试算例Fig.6 Standard test example of IEEE-39 bus system

3.1 样本构成

使用MATLAB 工具箱PST3.0 仿真计算生成暂稳数据集，PC 配置为：AMD Ryzen 5 PRO 4650G CPU 3.70 GHz/16GB RAM 3600 MHz。在标准IEEE-39 节点系统中全部34 条输电线路上分别设置三相短路故障，故障开始时间为0.1 s，故障持续时间从0.03～0.21 s 波动，步长为0.01 s，设置6 种从80%～120%随机波动的负荷水平，在距离每条线路左侧节点10%，50%，90%处设置3 种不同的故障位置。仿真时间为5 s，仿真步长为0.01 s，以仿真时间内发电机最大功角差是否超过360°作为样本功角失稳的判据。基于上述N-1 故障，最终一共生成了11 628 个样本，其中失稳样本个数为4 768，被标记为1；剩余6 860 个样本为稳定样本，标记为0。

单个样本包含10 台发电机的电磁功率、9 台发电机的功角（另一台为参考发电机）、39 条母线的电压，一共58 维特征，每个特征包含40 个时间节点的信息（0.06～0.45 s，步长为0.01s，故障发生时刻统一为0.1 s），因此每个样本包含58×40=2 320 维特征。

将样本重新排列成二维矩阵，选择2 个典型样本，其原始图像见图7。

图7 2个典型样本原始图像Fig.7 Original images of two typical samples

原始图像中自上而下分别是母线电压区、发电机功角区、发电机电磁功率区，在这种灰度图中，灰度值越大越接近白，1 代表全白；越小越接近黑，0代表全黑。可以观察到，稳定样本在母线电压区更白，表示电压基本稳定在1.0 p.u.附近，没有发生电压失稳，而功角失稳常常伴随电压降落，因此失稳样本电压区更黑；发电机功角区则相反，失稳样本由于不同电机功角摆开，功角差逐渐增大，因此显得更白。

3.2 模型验证以及不同模型对比分析

为了验证本文所提方法的有效性，选择在二分类问题中常用的支持向量机（Support Vector Machine，SVM）、随机森林（Random Forest，RF）、多层感知机（Multilayer Perceptron，MLP）以及不采用2D-PCA 降维的普通CNN 与本文所提方法进行对比。由于在TSA 中，我们往往更加关注模型对失稳样本判断，因此本文以准确率AC、失稳样本的误判率P1和漏判率P2作为评估指标，计算公式如下：

式中：TP为将真实稳定样本预测为稳定的样本个数；FP为将真实失稳的样本预测为稳定的样本个数；TN为将真实失稳的样本预测为失稳的样本个数；FN为将真实稳定的样本预测为失稳的样本个数。

由于SVM，RF 和MLP 模型无法直接处理图像数据，故将特征展开为一维向量并归一化后作为原始输入数据。SVM 和RF 采用网格搜索法和十折交叉验证进行参数寻优，计算得SVM 采用径向基函数（Radial Basis Function，RBF）为核函数，最佳目标函数的惩罚系数C=100，核函数系数γ=0.125；RF 的最佳树个数NU为120、树的最深深度MD为15、树的最大特征数量MF为12；MLP 的网络结构设置为和各层的神经元个数为64-256-128-32-2；本文所提方法降维后的特征维度为10。

3 种方案与本文所提方法的结果对比如表1 所示，所有方案的样本划分均为训练集：验证集：测试集=6：2：2。

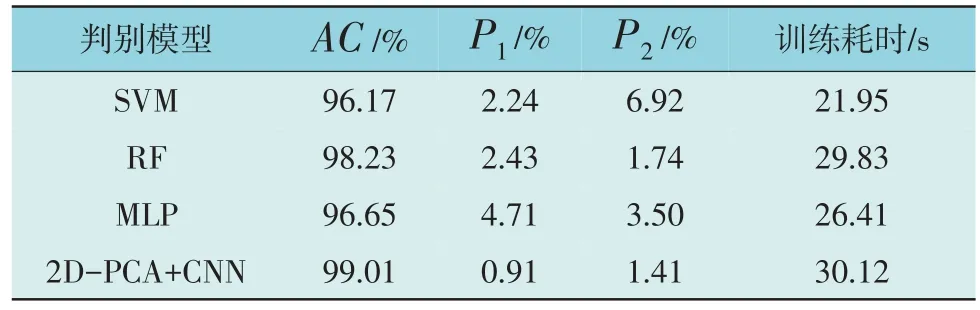
表1 不同模型对比结果Table 1 Comparison results of different models

表1 结果表明，本文所提方法在精度、误判率和漏判率较前3 种都有明显的优势，而由于深度学习涉及多层神经网络的误差传递和计算，训练时长上有所增加。在实际电网中，由于特征降维对运算量的减少会更加明显，本文提出的基于2D-PCA 和CNN 的判别模型在训练耗时上会取得更大的优势，能够满足模型在线预测和更新的要求。

此外，将本文降维方法与现有常用特征筛选或降维方法进行对比，其中特征筛选方法为过滤式（Filter），筛选标准为特征的信息增益，筛选后的特征维度为10；特征降维方法为PCA，降维后的特征维度为10。

表2 结果表明，经过降维后，相比CNN，其它模型的训练时长都大幅下降，Filter+CNN 模型和PCA+CNN 模型测试精度都有所降低，而本文所提方法测试精度提高，这是因为图像化输入数据加强了不同特征间的信息融合。

表2 不同特征筛选或降维方法对比结果Table 2 Comparison results of different feature screening or dimensionality reduction methods

3.3 特征提取可视化

t-分布随机近邻嵌入（t-distributed Stochastic Neighbor Embedding，t-SNE）是一种非线性降维算法，能将高维空间中的数据集投影至二维或三维的嵌入空间中，在保留原始信息的同时实现数据可视化[25]。

2D-PCA 目标寻找最优的投影向量，在对特征进行降维的同时使样本尽量分散开便于后续的特征提取，处理后的样本分散度越高表明投影向量对样本的分辨能力越强[26]。本文通过t-SNE 算法将原始样本以及经过CNN 模型训练后的样本投影到二维空间，如图8 所示，Feature 1 和Feature 2 为嵌入空间的两维特征（无量纲）。可见，经过CNN 的特征提取过程，样本的可分性显著增加。

图8 CNN训练前后对比Fig.8 Comparison of CNN before and after training

在利用CNN 模型训练样本前，先对样本进行2D-PCA 变换，结果如图9（a）所示，可见，经过2DPCA 处理后的样本分散程度明显提高，正负样本的区分度也有一定程度提升，方便了后续CNN 提取特征。为了直观地展示后续CNN 网络对原始图像的特征提取以及学习表达过程，利用t-SNE 将模型各层的输出结果投影至二维平面，结果见图9。

图9 CNN提取特征可视化Fig.9 CNN feature extraction visualization

从图9 可以看出，随着网络层数的增加，正负样本由最开始的互相交错重叠逐渐分离，直到最后两类样本之间已经出现明晰的边界，近乎线性可分。由此可见，CNN 具有强大的特征提取能力，通过对原始输入特征进行多级的信息筛选和提取，将其变换为与稳定状态强相关的高维特征，最终有效实现暂稳判别。此外，对比图8（b）与图9（d）可见，在对原始图像进行2D-PCA 降维后，训练后的模型对样本区分性能变得更强，符合预期结果。

3.4 模型在线更新能力测试

模型在线更新的关键在于确定合适的样本更新单位K和样本最大数量N，在保证对新样本精确判断的同时需要尽可能减少投影矩阵的计算次数和计算时长。为了寻找最佳的K和N，基于IEEE-39 系统，在BUS4 上新增BUS40 和发电机G11，并新增线路BUS4-BUS20，BUS4-BUS27，如图10 所示。在此工况和拓扑结构下对新系统进行暂稳仿真，一共生成11 270 个样本，其中失稳样本数量为3 107，稳定样本数量为8 163。

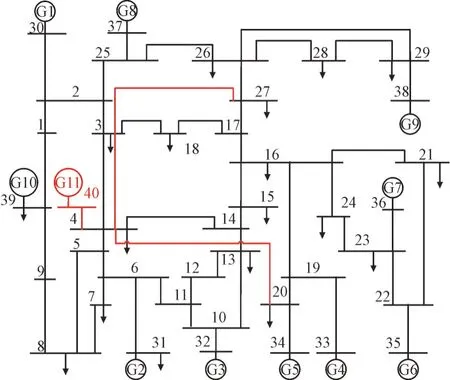
图10 新的运行方式Fig.10 New operation mode

利用在基础运行方式下得到的初始模型M0以及投影矩阵W0，设置精度最低期望值ACset=0.97，在新的运行方式下进行在线更新，直到更新完所有样本。图11 为（K，N）=（200，2 000）的某一次更新过程，可见随着模型的更新，其对新样本的判别能力也越强。

图11 某次模型更新过程Fig.11 A model update process

为了研究样本更新单位和样本最大数量对TSA模型预测精度的影响并寻找最佳的K和N，设置不同的K和N，分别在新的运行方式下进行实验，结果如图12。

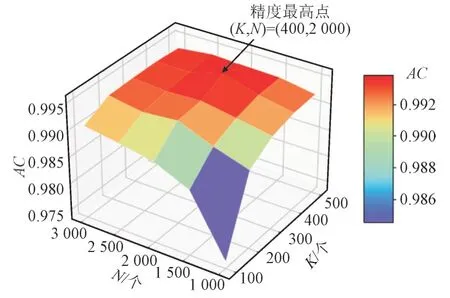
图12 不同K和N下模型更新的精度ACFig.12 Accuracy AC of model updating under different K and N

由图12 可见，尽管更新策略不同，但更新完所有样本后，模型在整个新运行方式下对所有样本的预测精度高于0.975，再一次验证了本文提出方法的有效性。当（K，N）=（400，2 000）时，TSA 模型的预测精度最高，达到0.995，故最佳的样本更新单位为400，样本最大数量为2 000。

4 结论

本文针对目前暂态稳定评估领域深度学习算法在真实电网中难以进行在线监测和更新的问题，提出将电气信息矩阵转换为更加高效的图像形式，采用2D-PCA 对原始图像进行特征降维，然后利用CNN 建立TSA 模型，并设置合适的样本更新单位以及样本最大数量进行模型的在线更新，在保证模型对新样本预测精度的同时提高了模型的更新效率，最终实现TSA 模型的实时监测和在线更新。

在IEEE-39 节点测试系统中进行仿真分析，算例结果表明深度学习算法CNN 的预测精度高于其他算法，在增加2D-PCA 进行特征降维后，计算速度大幅增加，能够满足在线化的需求。此外，本文还研究了不同的样本更新单位K和样本最大数量N对模型在线更新的影响，结果表明选择合适的K和N能够提升模型的预测精度并显著提高模型的更新效率，最终能够实现TSA 模型的在线评估。

在后续研究工作中，可以考虑利用其它更加轻量化的深度学习模型，进一步提升模型训练的效率和准确度。