分布式储能运行规划一体的多目标选址定容方法

方 磊，薛云霞，池宇琪，金 峰，刘 明，陈兵兵，刘 俊

（1.国网山东潍坊供电公司，山东潍坊 261000；2.西安交通大学电气工程学院，陕西西安 710049）

0 引言

近年来新能源装机容量迅猛增长，新能源渗透率也节节攀升，由于风光电源出力易受天气环境影响，其出力的间歇性、波动性会对电网电压稳定造成冲击[1-3]；分布式风光电源还会改变系统潮流、造成线路堵塞，且其出力的反调峰特性还使弃风弃光的现象愈加频繁[4-6]。分布式储能（Distributed Battery Energy Storage System，DBESS）具备双向功率输出、能量时移、快速响应等优点[7-8]，是解决高新能源比例配网诸多问题的最优选项之一[9-12]。

目前DBESS 在配网中的选址定容优化框架主要分为单层和双层两种[13]。双层优化框架主要是将规划时间尺度分离，文献[14-16]将储能安装位置和额定容量作为上层变量同时也作为下层须满足的约束条件，下层则大多以储能出力为决策变量，通过这种上下层相互迭代求解方式求解分布式储能选址定容模型，双层结构能够更好地分离不同时间变量，对其分别进行求解，但这种结构也存在储能容量冗余、求解时间长、难收敛等问题。在单层优化框架方面，着重解决的是不同时间尺度变量的耦合问题，文献[17]通过最大连续充放电量方式对储能容量进行校验。文献[18]还考虑了多类型的分布式电源规划，文献[19]将风光资源与负荷的耦合性也加入模型的构建中，文献[20]则主要针对功率时序不平衡引起的电压越限问题进行DBESS 规划。

考虑到配网中的分布式电源单机容量小、位置分散、出力波动性大，且系统的集中控制变量过多过程复杂，分区控制方法越来越成为解决配网控制的主流方法[21-22]。文献[23]提出了一种根据节点电压灵敏度对集群内各储能进行功率分配的调压控制策略，但仅将经济性作为优化目标，电压作为约束，无法进一步提升配网的电压质量。文献[24]提出了一种分布式光伏与储能的双层协调选址定容模型，上下层分别以综合费用和网损最小为目标将分布式光伏和储能分别配置到各个节点，但所提优化框架中没有考虑储能的优化运行策略，定储能出力曲线无法保证储能工作在最佳出力点。

针对现有研究中存在的单目标规划的储能应用场景单一[17]、位置变量不进行针对性编码导致的优化难收敛[13]、双层模型优化时间长以及不考虑DBESS优化运行[24]等问题，本文提出了一种基于集群划分的DBESS 运行规划一体的多目标选址定容方法。本文对配网进行集群划分，基于划分结果，建立以配网购电成本、储能日均成本、电压波动和网损为优化目标的DBESS 选址定容模型；针对第三代非支配排序遗传算法[25]（the Third-generation Non-dominant Sequencing Genetic Algorithm，NSGA-III）在处理位置变量时存在的问题[26-27]，提出一种改进的交叉偏移操作方法，且对目标和多时间尺度规划变量分别采用嵌入式潮流和混合编码的方式[28-29]进行处理；使用改进后的NSGA-III 算法对模型进行求解，在IEEE33节点配网模型上验证了所提模型和方法的有效性。

1 基于集群划分的储能配置模型

1.1 配网多目标集群划分方法

在进行DBESS 配置之前先对配网进行集群划分，文献[22]提出了模块度、有功和无功平衡度的综合性能指标，本文参考该文献采用了系统模块度指标f1，并对有功平衡度f2及集群功率波动性指标f3进行了相应的改进：

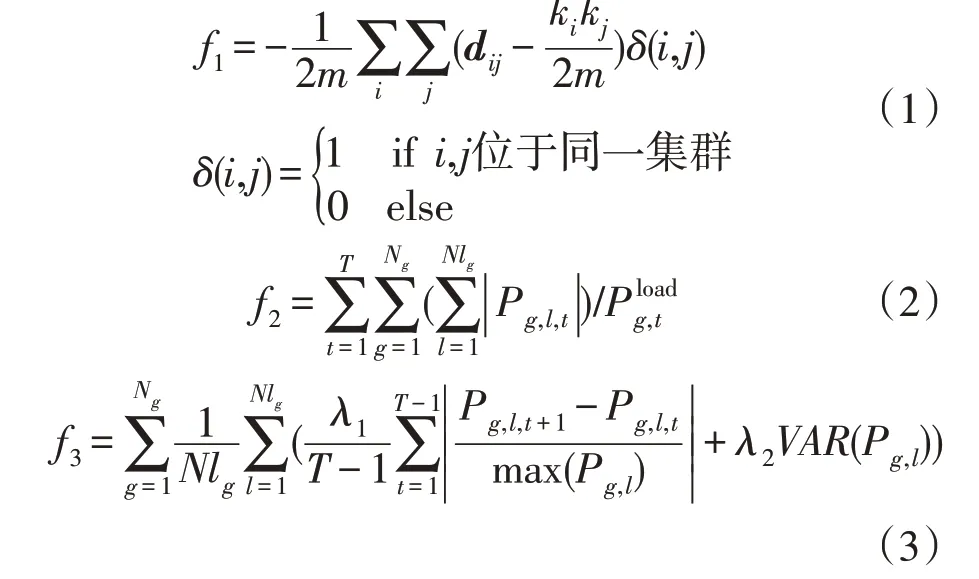
式中：dij为网络边权邻接矩阵，这里选用电压幅值/有功功率灵敏度矩阵确定的节点空间电气距离矩阵作为邻接矩阵；m为网络边权总和；ki为与节点i相连的节点边权总和；δ(i,j)=1 表示节点i与节点j位于同一集群内；Ng为集群的数量；Nlg为集群g与外界交互的联络线的数量；Pg,l,t为集群g线路l在t时段的功率平均值；为集群g在t时段内的负荷均值；f3中联络线功率波动分为两部分，λ1为第一部分顺序波动幅度的对应权值，λ2为第二部分联络线Pg,l在时段T内的方差。

改进的优化目标式（1）—式（3）和文献[22]中提到的其他约束一起构成了本文提出的配网多目标集群划分模型，在IEEE 33 节点配网上使用改进的NSGA-III 算法进行求解，使用基于TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）的多属性决策方法从得到的Pareto 解集中选出最优解。求解时，权值λ1,λ2分别设置为0.5，0.5。得到的集群划分结果如图1 所示。

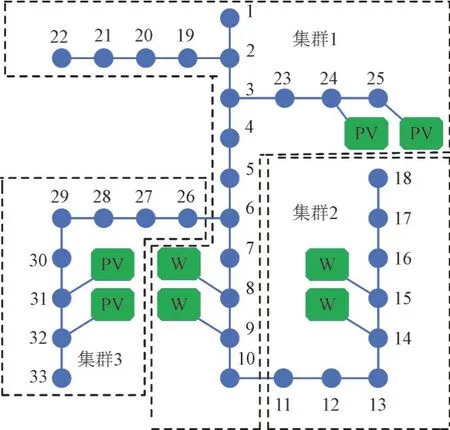
图1 配网多目标集群划分结果Fig.1 Result of distribution network multi-objective cluster division

1.2 多目标DBESS选址定容模型

含高比例新能源的配网存在电压波动大、网损增加等问题，在配网中分布地配置储能装置能很好地解决这一难题，但DBESS 目前的价格仍居高不下，在配置时，其功率和容量大小也是需要考虑的重要因素。为减小调峰压力，分时电价也逐渐在全国推广应用，在此环境下，储能也可发挥其能量时移特性，减小配网购电成本。因此，考虑配网运行的经济性和安全性指标，选取了配网购电费用F1，储能日均运行成本F2，电压波动F3，网损F4作为优化目标：

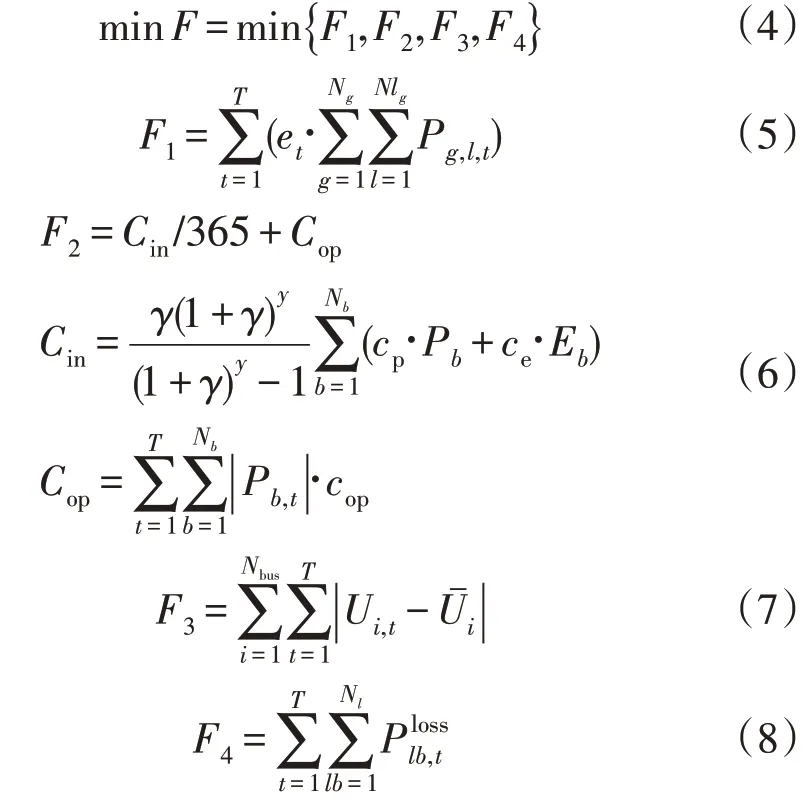
式中：et为t时段向主网购电的实时电价；Cin为DBESS 的年化投资成本；Cop为储能的日均运行维护费用；γ为银行利率；y为储能使用年限；Nb为配网中第b座DBESS 的数量；cp,ce分别为DBESS 的功率、容量的单位安装费用；Pb,Eb分别为第b座DBESS 的功率和容量；Pb,t为第b座DBESS 在时段t内的功率；cop为其单位运行维护费用；Ui,t为节点i在时段t内的电压均值；Uˉi为规划总时段数T内的电压均值；Nl为配网的支路数；Nbus为配网中节点的数量；为支路lb在t时段的线路损耗功率。DBESS 选址定容模型的决策变量涉及DBESS安装位置的0-1 变量和储能出力的浮点数变量，因此本文采用混合编码方式如式（9），并在NSGA-III的交叉变异操作中对不同类型的变量采用不同的操作方式。

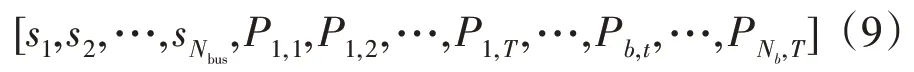
式中：si=1 表示节点i配置了储能，si=0 表示节点i没有配置储能。

对考虑集群划分的DBESS 进行选址定容时除了满足电压偏差范围约束、潮流约束、功率平衡、DBESS 充放电等常规约束，还需要满足集群内储能数量恒定的约束，具体如下：

1）电压偏差范围约束。

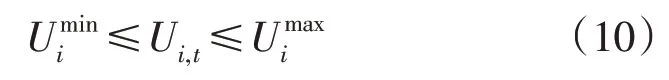
2）潮流约束。

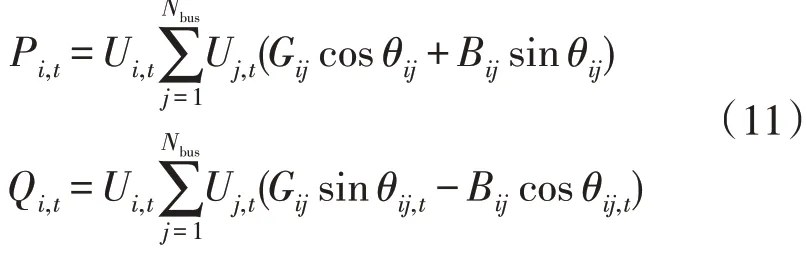
式中：Pi,t,Qi,t分别为节点i在t时段的有功功率和无功功率；Gij,Bij分别为节点i和j间的电导和电纳；θij,t为节点i和j间的电压相角。

3）有功功率平衡约束。

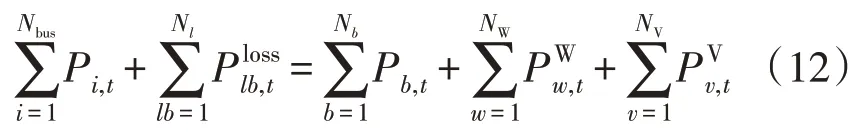
式中：NW为分布式风场的数量；为第w座分布式风场在时段t内的发电功率；NV为分布式光场的数量；为第v座分布式光场在时段t内的发电功率。

4）DBESS 充放电约束。

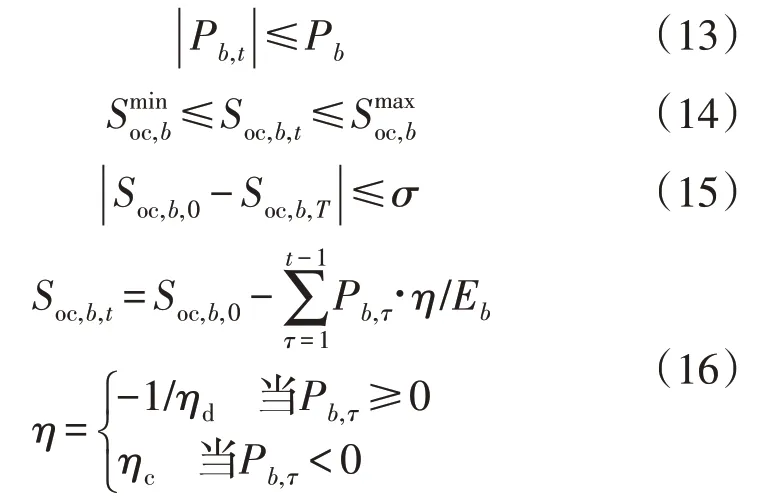
式中：Soc,b,t为第b座DBESS 在t时段末的荷电状态，分别为第b座DBESS 荷电状态的上下限；σ为DBESS 首末荷电状态最大偏差幅度，设置为0.1；Eb为 第b座DBESS 的额定容量，η为DBESS的归算充放电效率；ηc,ηd分别为DBESS 的充放电效率。

为提升优化效率，DBESS 的额定容量Eb采用最大累计充放电量E′b和最大单次充放电量E″b来计算，具体计算如下：

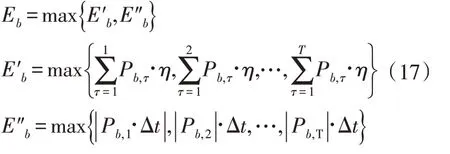
式中：Δt为t时段的时间跨度。

5）DBESS 集群数量约束。

式中：和Sg分别为集群g包含的节点数目和DBESS 数目。

2 改进的NSGA-III多目标优化算法

2.1 多目标DBESS选址定容优化框架

求解多目标DBESS 选址定容模型是一个混合整数非线性的多目标问题，NSGA-III 是一种在遗传算法基础上改进的多目标优化算法，在求解该类问题方面具有较高的求解效率。前代NSGA-II 与NSGA-III，两者在框架上基本相同，不同的是NSGAIII 摒弃了前者基于拥挤度的非支配排序方法，转而改用基于参考点的非支配排序方法。NSGA-III 在处理目标数大于3 的优化问题时，非支配个体呈指数增长而导致的个体间难以进行优劣区分的难题得以有效解决，在处理高维优化问题时相比于NSGA-II和其他多目标进化算法具有更高的效率和分布性更好的解集。因此，本文提出了多目标DBESS 选址定容优化框架，如图2 所示，其中G,G_max 分别为当前节点的迭代次数和最大的迭代次数。

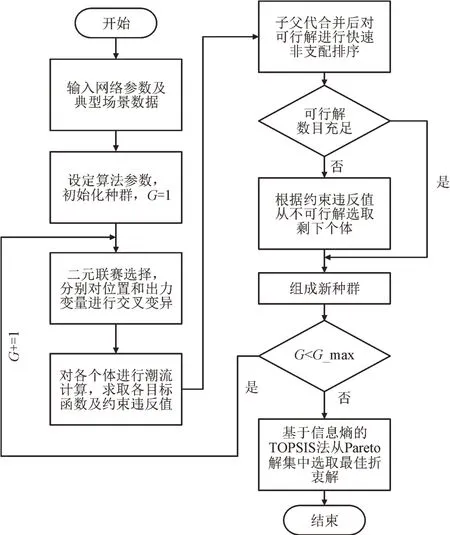
图2 多目标DBESS选址定容优化框架Fig.2 Multi objective DBESS location and capacity determination optimization framework

2.2 偏移交叉操作方法

各个集群内部储能位置的选取虽然采用0-1编码方式，但其0-1 符号表征对应节点无/有配置储能而不是二进制的0-1。分集群配置分布式储能的问题中需要保持各集群内储能数量恒定，为此会导致迭代过程中的不可行解的数目增加，问题的求解难度也大幅增加，为此提出针对位置变量改进的偏移交叉操作方法，把约束（18）融合在改进后的交叉变异中。具体步骤如下：

1）采用二元联赛选择法从种群中不放回地两两选择个体依次排序，前后两个个体以交叉概率pc进行交叉。

2）选中待交叉的两个个体，假设其在集群g的储能位置分别为位于该集群内的第a,b和c,d个节点，即对应的位置变量sa=sb=1,sc=sd=1；参考模拟二进制交叉操作，交叉前后的变量应满足a+b+c+d=a1+b1+c1+d1，随机偏移概率为pi，当rand()＞pi则两个体位置直接进行交叉，不对位置进行偏移；当rand()≤pi，则随机生成两个在[-2，2]区间的随机整数r1,r2，其交叉后的位置为a1=c+r1,b1=d-r1和c1=a+r2,d1=b-r2，即交叉后两个个体的集群g中，sa1=sb1=1，sc1=sd1=1，对交叉后的个体重新进行校验，防止位置溢出集群。

3）对于交叉后的个体以变异概率pm进行变异，变异操作为在各集群内随机进行储能的选点覆盖原来的位置。

通过这种改进的交叉变异操作，式（18）直接嵌入交叉变异操作中，即满足了约束条件，也保留了交叉变异的遗传特性，使得可行解的数目增加，利于模型的求解。同时，为改进收敛性，这里采用动态的交叉、偏移、变异概率。

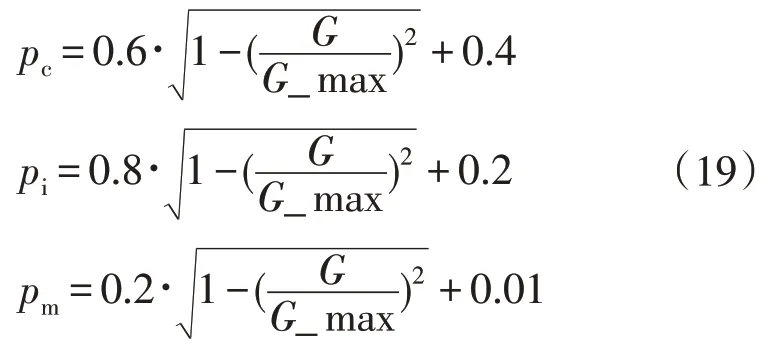
2.3 Pareto约束支配方法

对于模型需满足的电压偏差范围约束和DBESS 的首末电量约束，本文采取Pareto 约束支配方法对其进行处理，相比于罚函数的处理方式，约束支配不会掩盖目标函数本身的真实性从而避免影响解集分布的均匀性。

对于多目标约束问题：

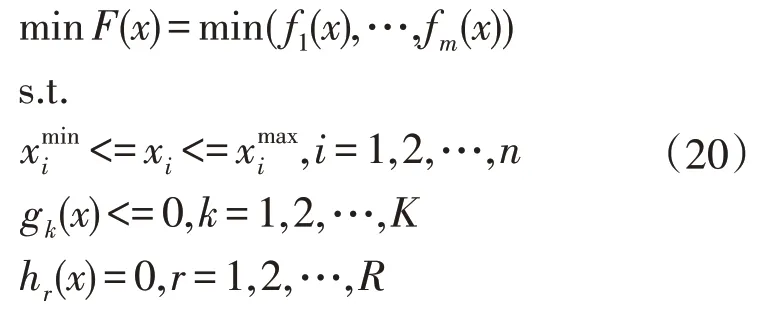
式中：f,x分别为优化目标和待优化变量；fm为第m个优化目标；xi为第i个待优化变量；分别为变量xi取值的上下限。

对于不等式约束gk(x)和等式约束hr(x)，全部满足约束的解为可行解，反之为不可行解。对于不可行解，采用约束违反值CV(x)衡量来定量描述一个解违反约束条件的程度。

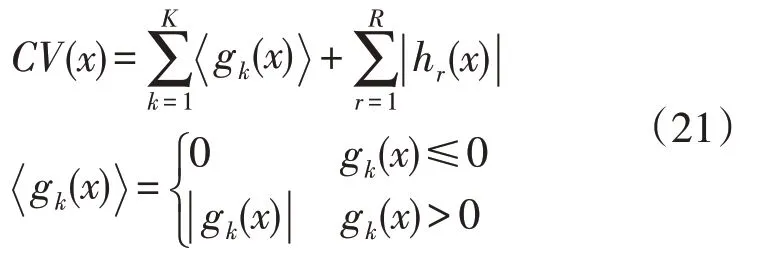
对于一个可行解，其CV值为0；对于不可行解，CV值越小，其违反约束的程度越低。

当满足以下条件任何1 项时，意味着在约束支配关系中，解m支配解n：（1）m为可行解，n为不可行解；（2）m,n均为不可行解，但CV(m)＜CV(n)；（3）m,n均为可行解，并且m帕累托支配n。

在选取下一代种群的过程中，优先从可行解中选取，若数目不足则从不可行解中根据CV值选取剩余个体。

3 算例分析

本文使用IEEE33 节点配网的网架参数，风光荷典型场景来源于山东潍坊市统计数据。仿真场景设置如图3 所示。

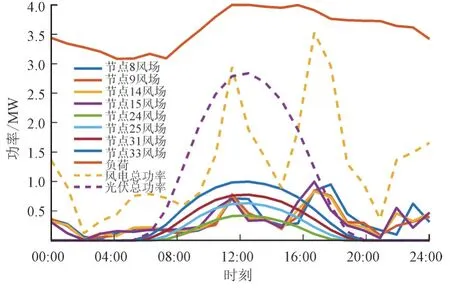
图3 场景设置Fig.3 Scene setting

图3 中，在节点8，9，14，15 上各安装了2 MW的分布式风电场，在节点24，25，31，32 上各安装了1.5 MW 的光场，最大负荷4 MW，该场景下新能源渗透率为60%，集群划分结果见图1。各集群节点数目为17，8，8，因此各集群内的储能数目分别设为2，1，1。DBESS 采用锂电池基材储能装置，单位功率成本为1 500 元/kW，单位容量成本为3 000 元/kWh，单位运行维护成本为0.08 元/kWh，银行利率为0.08，设定储能使用寿命为10 年。

为了证明本文所提DBESS 选址定容方案的优越性，设置对比方案如下：方案1 本文所提方案；方案2 不进行集群划分的DBESS 选址定容方案；方案3 不配置储能。

3.1 算法收敛性及计算时间对比

目前有不少研究着重于双层优化框架，即上层为储能位置、功率、容量，下层为优化储能出力，此类型优化突出的问题在于计算时间长。本文采用仿真平台的CPU 为锐龙4 650 g 台式计算机，软件为Matlab2020b。为体现本文提出的运行规划一体的单层优化框架在计算效率方面的优势，与使用优化后的NSGA-III 算法的双层优化框架计算结果对比如表1 所示。

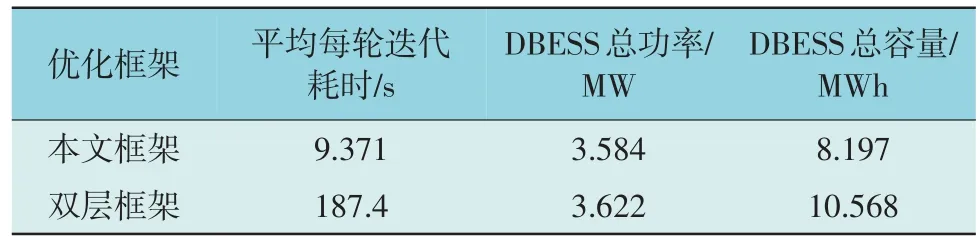
表1 单层、双层优化框架结果对比Table 1 Comparison of single-layer and double-layer optimization frames results

从表1 可以看到，本文提出的融合变量后的单层优化框架平均每轮迭代耗时为双层框架板的5%，主要是双层优化框架中上层的迭代更新都依赖于下层优化的完成，因此每轮迭代都需要下层反复进行潮流计算来更行目标函数，其潮流计算次数是本文提出优化方法的20 倍以上。同时，本文采用的DBESS 额定容量的校验方式也使得变量数目减少，且优化得到的DBESS 功率和容量更小。

将改进后的NSGA-III 算法与未改进的NSGA-III算法和基于分解的多目标进化算法（Multi-objective Evolutionary Algorithm Based on Decomposition，MOEAD）进行对比，在迭代中各轮最优Pareto 层的解数目如图4 所示。从图4 中可以看到，得益于对位置变量约束关系的偏移交叉操作，改进后的NSGA-III在每轮迭代过程中得到的最优Pareto 层解集的数目都要优于未改进的NSGA-III 算法和MOEAD，有利于求解得到分布性和性能指标都更好的非支配解集。

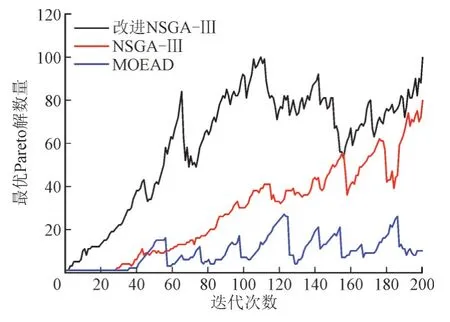
图4 迭代中最优Pareto解集数量对比Fig.4 Number comparison of optimal Pareto solution sets in iteration

3.2 规划结果分析

方案1 使用基于TOPSIS 的多属性决策方法得到各目标的评价权重为0.208:0.355:0.213:0.223，以相同方法得到方案2 的评价权重为0.162：0.222：0.356:0.258；由此得到各方案的最优DBESS 配置方案、优化目标分别如表2、表3 所示。

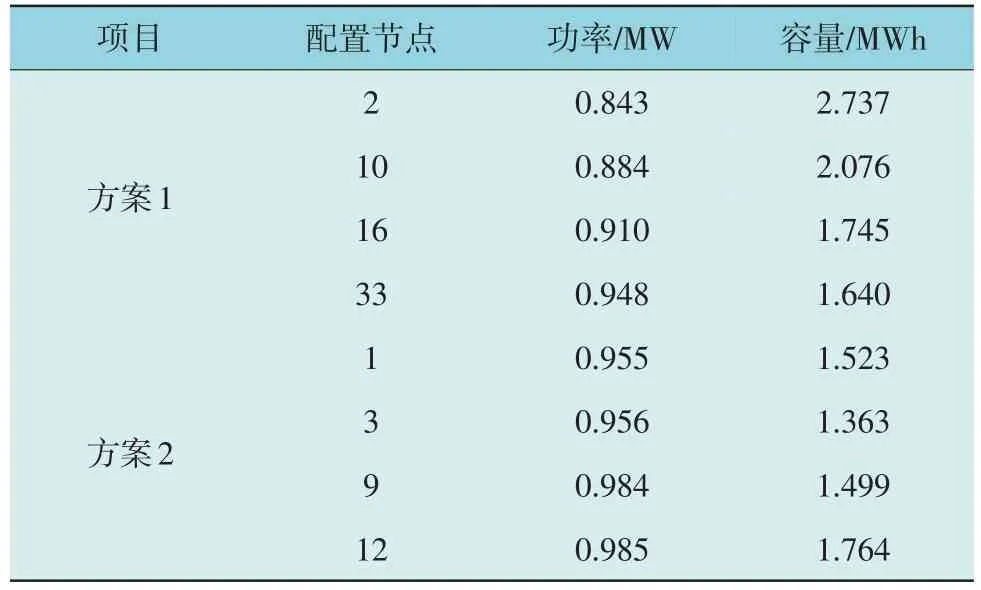
表2 DBESS配置结果Table 2 DBESS configuration results

各方案的目标优化如表3 所示。

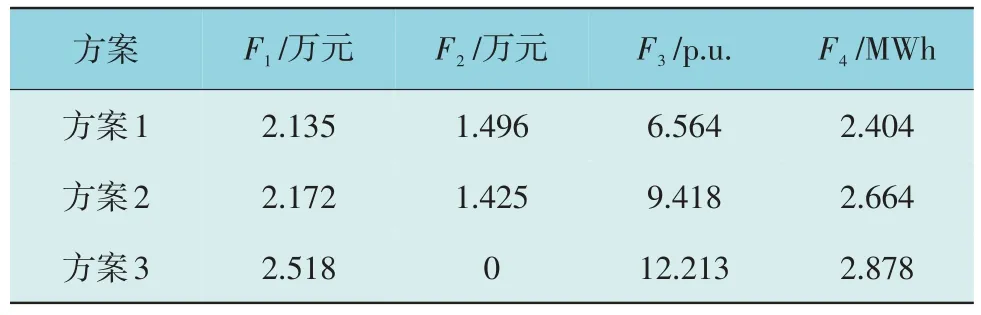
表3 各方案优化目标Table 3 Optimization objectives of each scheme

由表2、表3 可以看到，与不配置DBESS 的方案3 相比，方案1、2 在配网购电成本、电压波动、网损上均有明显降低，证明DBESS 在进行能量套利、削峰填谷、改善电能质量方面具有重要作用。方案1 与方案2 相比，虽然DBESS 日均费用有所增加，但配网购电费用、电压波动、网损方面相比方案2分别降低了1.7%，30.3%，9.76%，且方案2 与方案1相比，DBESS 存在扎堆配置的情况，说明了基于集群进行规划能够使DBESS 更加合理分布，能够给偏远节点提供电压和功率支撑，改善系统潮流、降低网损。

3.3 运行结果分析

1）DBESS 优化运行结果。

DBESS 优化运行结果如图5 所示，相比于不加DBESS 的方案3，本文所提方法能使整个配网的净负荷尽可能均匀地分布在1 d 中的各时段，在新能源高发期10:00—18:00，DBESS 充电吸收过发的新能源功率以降低净负荷峰值，在其他时段DBESS 主要放电进行能量套利以及平衡新能源发电低谷，因此方案1 的净负荷峰谷差从方案3 的5.088 MW 降低到了2.994 MW，降低了41.16%，而配网购电费用从2.518 万元降低到了2.135 万元，降低了15.21%。

图5 DBESS优化运行结果及配网净负荷对比Fig.5 Optimized operation results of DBESS and payload comparison of distribution network

2）电压波动情况。

选取分布式光场和风场所在的节点来对比分析电压波动情况，因方案1、方案2 电压波动差异比较小，这里仅选取了方案1（图6 中实线所示）与方案3（图6 中虚线所示）相比，方案1、方案3 电压波动情况如图6 所示。

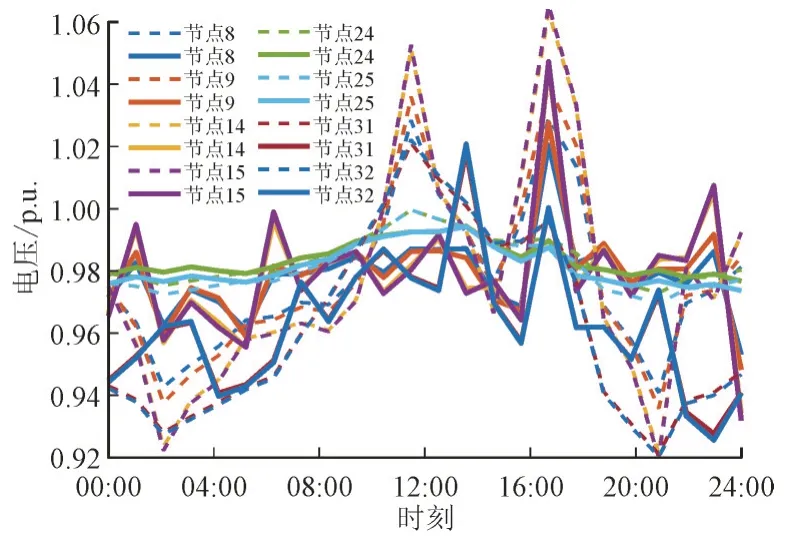
图6 各节点电压波动情况Fig.6 Voltage fluctuation of each node

由图6 可以看到，大部分实线的总体波动情况要小于相同的颜色的虚线，说明在加入DBESS 之后，方案1 电压波动情况相比方案3 有显著改善，电压波动降低了46.25%。

3）网损分布对比。

1 d 中3 个方案在规划典型场景各时段的全网网损情况如图7 所示。由图7 可以看到，分布式新能源在高发期间会增加配网的网络损耗，且方案1相比于方案2 和方案3，网损分别降低了9.76%和16.47%，其在大部分时间的网损都维持在较低水平，说明分集群配置储能不仅可使区域功率平衡、降低电压波动，最大的优点在于还可改善系统潮流分布，减少网损。

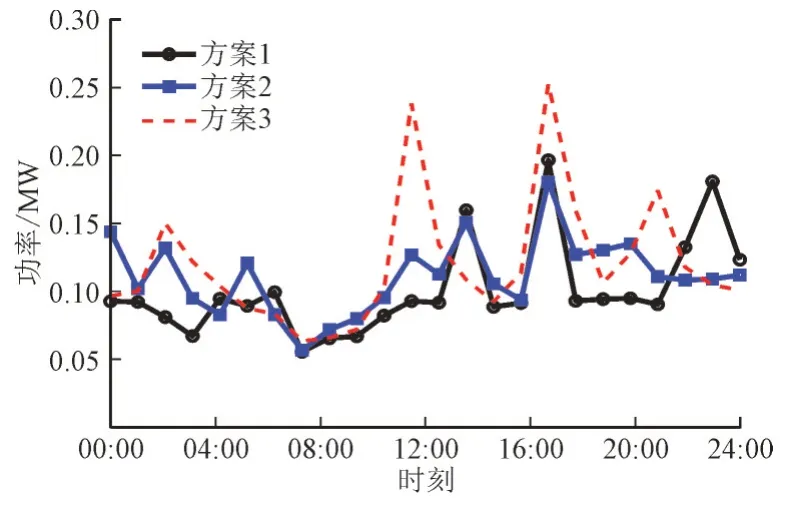
图7 各方案网损对比Fig.7 Comparison of network losses of various schemes

4 结论

本文基于配网集群划分结果，以购电费用、DBESS 日均成本、电压波动和网损的经济性和安全性指标为优化目标，构建了DBESS 运行规划一体的多目标选址定容规划模型，并使用改进的NSGA-III算法对模型进行求解。与多种方案和算法进行对比，得到的结论如下：

1）本文构建的DBESS 运行规划一体的选址定容模型相比于双层优化模型，在保证求解精度的同时大幅度减少了求解时间；针对位置变量提出的交叉偏移操作方法，使得改进后的NSGA-III 相比于其他多目标优化算法得到的帕累托支配解的数量更多。

2）配网中加入DBESS 能够提升分布式新能源消纳，降低配网净负荷峰谷差，且可以通过响应分时电价进行能量套利，降低配网购电费用。

3）分集群配置DBESS 的方法相比全局配置方法能够使DBESS 的规划接入点分布更加均匀合理，能够给配网中的偏远节点提供更好的电压和功率支撑，并且可以改善系统潮流分布，进一步降低网损。

后续研究将考虑多场景下分布式电源和储能的联合规划方法。