一种新的求解圆锥误差补偿系数的算法∗
2022-12-01 03:40:38耿腾飞胡正兴
舰船电子工程 2022年3期
耿腾飞 刘 明 胡正兴
(1.云南民族大学 昆明 650031)(2.昆明七零五所科技发展有限责任公司 昆明 650118)
1 引言
在捷联惯导系统中,圆锥运动对姿态解算有很重要的影响。自Bortz提出转动矢量微分方程后[1],国内外学者已经对圆锥误差补偿算法做了一系列的研究[2~10],如文献[2]提出了三子样算法,文献[4]提出了在各种子样下求解圆锥误差补偿系数的一般算法公式[4],在此基础上,文献[11]针对盲目增加子样数和提高采样频率会引起更大圆锥误差的问题,提出了一种利用前两个周期陀螺输出角增量信息的重叠三子样补偿算法;文献[12]通过采用一种新的补偿模型来减小圆锥误差的常值漂移问题;文献[13]将在圆锥运动条件下常见的4种不同的姿态算法进行实验仿真与误差建模。文中考虑到经典的圆锥运动求解误差补偿系数时没有考虑到补偿效应相同项合并的问题,推导出了新的传统圆锥误差补偿系数的表示方式,在此基础上利用陀螺前周期角增量信息得到了改进的求解圆锥误差补偿系数的算法,通过比较精度比传统算法有所提高。
2 圆锥误差与旋转矢量
设Φ为旋转矢量,则旋转矢量的微分方程为[1]:

3 圆锥误差补偿算法

其中各字样角增量Δθi和总角增量θ表达式为

4 圆锥误差补偿系数求解


5 改进圆锥补偿算法
文献[5]提出利用前一周期陀螺角增量信息的改进圆锥误差补偿算法,但没有给出算法的一般公式,改进算法的一般形式为

6 应用


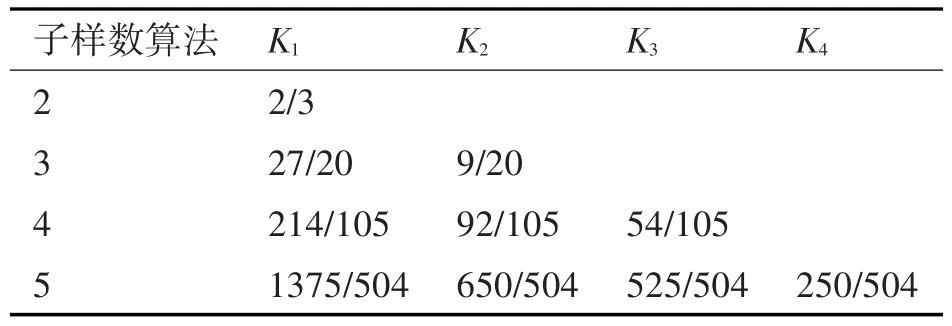
表1 2-5子样圆锥误差系数

7 结语
文中在传统求解圆锥误差系数算法的基础上,重新推导出一种新的求解圆锥误差系数的通用公式,列出了2-5子样的补偿系数,并在此基础上提出了一种改进的捷联惯导系统圆锥误差补偿算法,通过比较可得到在子样数相同的情况下新算法高出传统算法2阶的补偿精度,具有一定的应用价值。
猜你喜欢
中国农业大学学报(2022年10期)2022-09-22 11:01:12
中学生数理化(高中版.高考理化)(2022年5期)2022-06-01 06:27:42
中等数学(2021年6期)2021-08-14 02:35:50
小学生学习指导(高年级)(2021年6期)2021-06-19 05:37:32
哈尔滨轴承(2021年4期)2021-03-08 01:00:50
商品与质量(2020年16期)2020-07-29 00:50:44
小学生学习指导(低年级)(2019年10期)2019-10-16 08:12:34
山东工业技术(2019年9期)2019-05-29 11:07:08
学生天地(2019年6期)2019-03-07 01:10:46
军事文摘(2018年24期)2018-12-26 00:58:18

