淮北平原近57年多尺度水面蒸发悖论差异性研究

王 玥，王怡宁，雷晓辉，胡永胜，赵雯颉，鞠 琴

（1.中国地质大学，北京 100089；2.南京水利科学研究院南京 210029；3.河海大学，南京 210098；4.中国水利水电科学研究院，北京 100038；5.安徽省（水利部淮委）水利科学研究院五道沟水文实验站，安徽 蚌埠 233000）

0 引 言

全球水循环的变化会导致重大环境与社会经济影响。在全球温室效应显著的大背景下，随着全球平均气温的升高通常会导致陆地水体蒸发增加，而蒸发皿实测蒸发量反而下降，这种现象被称之为“蒸发悖论”[1]。国内外学者Peterson等[2]研究发现美国大部分地区蒸发呈下降趋势且主要因素为气温；N.Chattopadhyay[3]选取印度地区15 与32年不同时间序列资料对影响蒸发的因素进行相关分析，发现除气温外，相对湿度对蒸发量的影响也较为显著；左洪超[4]等利用线性、多元回归等方法验证了蒸发潜力受多气象要素综合作用且与相对湿度相关最好；Roderick[5]、朱晓华[6]等、鲍振鑫[7]等研究发现澳大利亚、中国、海河流域“蒸发悖论”现象主要成因为风速的下降；王楠[8]等研究发现我国地面风速整体呈下降趋势且春季下降速率最快，并得出该成因可能为气候变暖；Limjirakan[9]选取泰国1970-2007气象数据研究表明“蒸发悖论”现象主要因素除了风速的下降，还有日照时数的减少。钱筱暄[10]等研究发现淮北地区1964-2009水面蒸发量年、季蒸发量均呈现下降趋势，气温、地面温度、水汽压力差、日照及相对湿度是影响水面蒸发的重要因素；郝振纯[11]等研究发现五道沟地区年、季不同尺度水面蒸发影响因素不同，风速与降水的影响也较为显著；王怡宁[12]等研究得出五道沟地区“蒸发悖论”成因可能是太阳辐射的减少与气溶胶含量的增加；李秀[13]等、熊玉琳[14]等、宋培兵[15]等、刘敏[16]等主要采用气候倾向率、Mann-Kendall 检验等方法，分别对我国永定河、海河、通辽地区以及大黑河等不同区域的水面蒸发特征进行分析。

上述研究成果表明，国内外蒸发量总体均呈现出下降趋势，而不同地区及不同时间尺度蒸发量下降影响因素不同。淮北平原以往“蒸发悖论”相关研究主要以年、季尺度，本文选取五道沟1964-2020年近57年气象资料，采用气候倾向率法对淮北平原年尺度（1-12月）、汛期（6-9月）、非汛期（10-5月）及年代多时间尺度水面蒸发变化差异性进行研究，并运用多元回归分析法得到各尺度蒸发量回归方程及主要影响因子贡献率，为构建适用于淮北地区水面蒸发计算模型提供依据。

1 研究区域概况

五道沟水文实验站位于淮北平原南部，地处暖温带与亚热带的过渡地带，多呈典型半干旱半湿润季风气候，降雨年际年内分配十分不均，多年平均气温为15.0 ℃；降雨量为901.6 mm；水面蒸发量为1 038.6 mm。站内设有水文气象观测场、自动称重式地中蒸渗仪群、62 套大型地中蒸渗仪群、径流实验场及人工模拟降雨径流实验场等设备。

2 资料与方法

本文数据选取实验站气象场E601 型水面蒸发量（mm）、气温（℃）、降雨量（mm）、日照时数（h）、风速（m/s）、水汽压力差（mb）、相对湿度（%）的实测数据。水面蒸发悖论规律的研究采用1964-2020年的气象实测数据，对其变化以及突变趋势进行分析。

2.1 气候倾向率法

气候倾向率法[17]是指用一次线性方程来拟合各气象要素随时间变化。其代表各气象水文要素多年的变化趋势，通常以气象水文要素时间序列线性回归模型斜率的10 倍来表示各个气象因子的气候倾向率。即：

式中：i为时间序列年份；为样本量为n的各气象因子变量；ti为对应时间；a为常数项；b为气象要素的回归系数。设定显著性水平为0.05，选择MK-Z值、Sig值与T值检验气候倾向率是否通过显著性检验。

2.2 完全相关系数

皮尔逊相关系数[18]是描述两个序列相关性的统计量，本文采用此分析计算完全相关系数[12]。

式中：r为完全相关系数；rt为时间与各气象要素相关系数；re为蒸发量与气象要素相关系数。其中，相关系数均需大于临界值0.273 2（α=0.05）。

2.3 灰色关联分析

灰色关联分析相比传统多因素分析法，对数据要求较低且计算较为方便，应用较为广泛。本文将灰色关联分析运用到“蒸发悖论”成因分析研究中。具体计算步骤见[19,20]。关联度分为低关联(0 ,0.5 ]、较高关联(0.5,0.85 ]、高关联(0.85 ,1]3个等级。

2.4 Mann-Kendall检验

Mann-Kendall检验[21]是目前广泛应用的非参数检验法，本文采用MK检验对实验站蒸发量变化趋势及突变性进行分析。

2.5 贡献率分析

建立多元回归线性模型，计算蒸发量各影响因子的回归系数从而得出蒸发量回归方程。如拟合结果较好，则可用来分析各影响因子对蒸发皿蒸发量贡献率[22]。

式中：QX为各影响因子对蒸发量的贡献率；∆Ex为影响因子变化导致蒸发量变化值；∆E为实测蒸发量的变化值。

3 结果与分析

3.1 蒸发量与气温变化特征

五道沟地区多年平均气温、多年蒸发总量1964-2020年尺度、汛期、非汛期变化趋势图如图1(a)～图1(c)所示。由图1(a)可见，多年平均气温呈现缓慢上升趋势，且气候倾向率为0.27 ℃/10a。水面蒸发量整体呈现下降趋势，且气候倾向率为85.8 mm/10a，存在“蒸发悖论”现象。由图1(b)、图1(c)可见，汛期年平均气温以0.05 ℃/10a速率上升，而水面蒸发量以41.49 mm/10a 速率下降。非汛期年平均气温上升速率为0.27 ℃/10a，蒸发量下降速率为30.39 mm/10a。

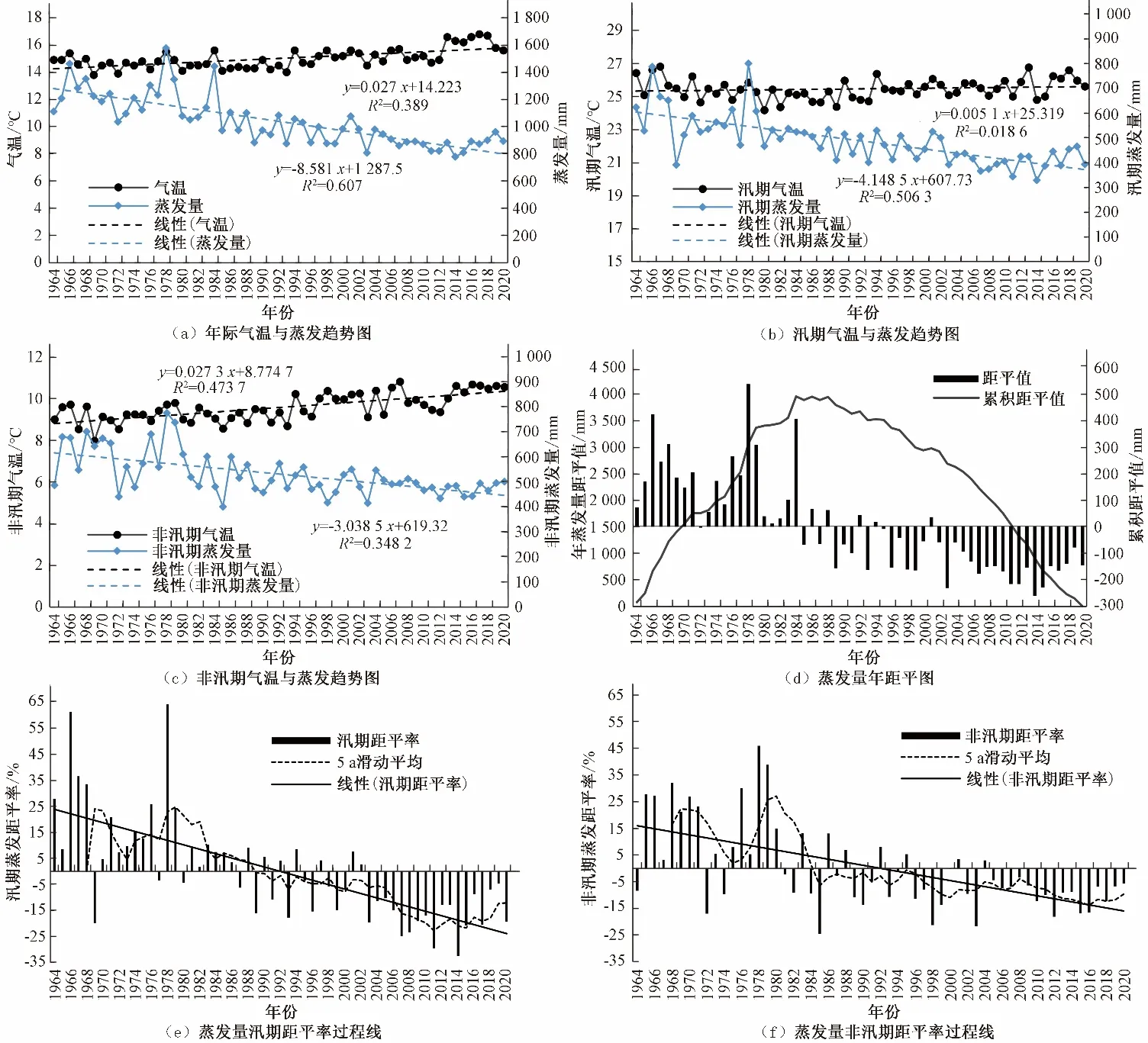
图1 1964-2020年尺度、汛期、非汛期变化趋势图Fig.1 Variation trend chart of scale,flood season and non-flood season from 1964 to 2020

由此可见，汛期气温升高速率弱于非汛期，而蒸发下降速率明显强于非汛期；年尺度与非汛期气温下降速率相等，但蒸发量下降速率远大与非汛期。由此可推断，汛期“蒸发悖论”规律更具显著性，排序为汛期＞年＞非汛期。

蒸发量年距平见图1(d)，其中1966-1984年间，均为正距平年且距平变化较明显；1985-2001年，距平值基本一正一负交替；2002-2020年均为负距平年，且年际距平变化较稳定。累积距平值呈现出明显先增后减趋势，且在20世纪80年代末达到峰值。

汛期及非汛期蒸发量率距平率过程线见图1(e)、图1(f)，可见汛期及非汛期距平率规律与年尺度规律基本一致。由图1中虚线距平率5 a 滑动平均值可见，1964-1992年水面蒸发变幅较大，基本为3～4年为一个周期，1992年后变幅较小。

气温、蒸发量年代变化过程见图2。平均气温20世纪70至80年代各尺度微弱下降，随后持续上升，且在21世纪10年代到达峰值；蒸发量20世纪70至90年代各尺度蒸发量均大幅下降，21世纪初非汛期蒸发量呈现微弱上升趋势，年与汛期缓慢下降。

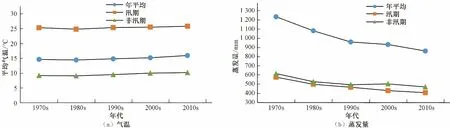
图2 气温、蒸发量年代变化趋势图Fig.2 Trend chart of temperature and evaporation in time

由此可见近5 个年代中，20世纪80年代气温上升0.37 ℃/10a，蒸发量下降122.67 mm/10a；该时段气温上升幅度最小，且蒸发量下降幅度最大，“蒸发悖论”规律最显著。21世纪以来，较20世纪末3 个年代，气温变幅增大，蒸发量变幅减小，“蒸发悖论”规律较不显著。

3.2 蒸发量与各要素变化趋势分析

蒸发量与各要素变化趋势分析采用Sig 值与T值对其气候倾向率进行检验，并结合MK-Z值对其变化趋势作进一步验证。水面蒸发与各要素气候倾向率与显著性分析见表1。

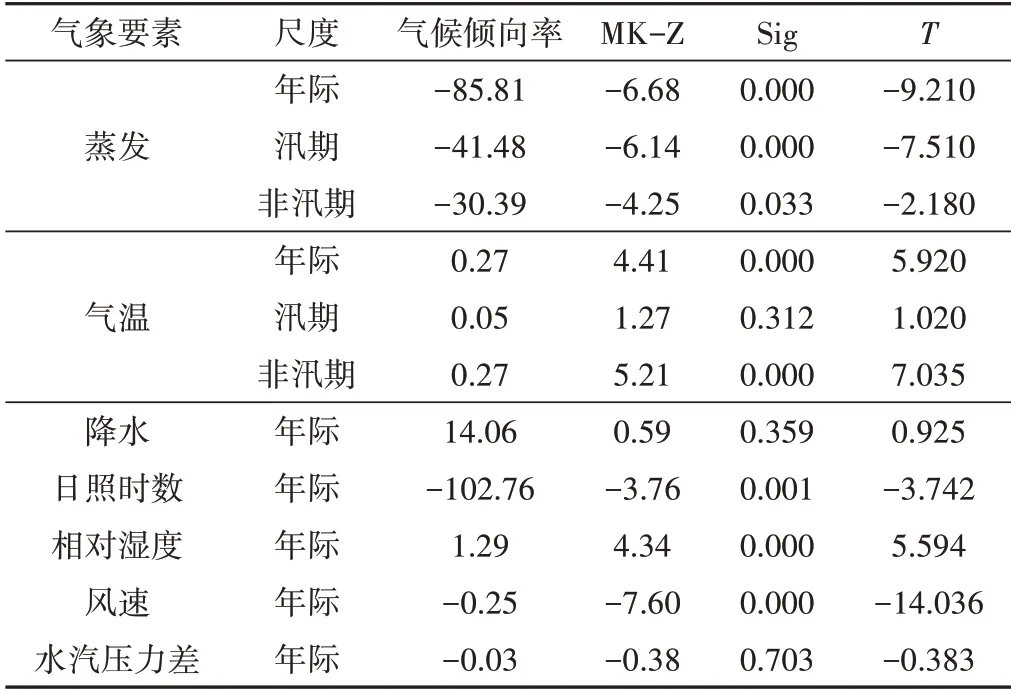
表1 水面蒸发与各要素多尺度气候倾向率与显著性分析表Tab.1 Analysis table of water surface evaporation and multi-scale climate tendency rate and significance of each element

由表1可知，水面蒸发量年尺度及(非)汛期的气候倾向率均小于0，显著性sig值小于0.05，MK-Z、t检验绝对值分别大于1.64、2.00，通过了α= 0.05 的显著性检验，表明水面蒸发量多尺度均存在显著下降趋势。

气温年际及(非)汛期的气候倾向率均大于0，年际与非汛期通过了α=0.05的显著性检验，表明气温呈现显著上升趋势；而汛期平均气温未通过显著性检验，无明显变化趋势。

降雨量以14.06 mm/10a 速率上升但变化不显著；相对湿度以1.29%/10a 速率显著上升；日照时数与风速气候呈显著下降趋势，气候倾向率分别为-102.76 h/10a 与-0.25 m·s-1/10a；水汽压力差无明显变化趋势，气候倾向率为-0.03 mb/10a。

3.3 蒸发量与气象因子相关性分析

为准确分析蒸发量变化的主要影响因子，揭示五道沟地区“蒸发悖论”成因，选取6 个气象因子：气温、日照时数、降水量、风速、相对湿度与水汽压力差，以年尺度与（非）汛期多尺度详细分析各要素与蒸发量的相关关系与关联度，见表2。其中，rt为时间与各气象要素相关系数；re为蒸发量与气象要素相关系数，当rt与re均大于临界值0.273 时，计算完全相关系数|r|。

由表2可知，年风速与蒸发呈显著正相关，相对湿度与蒸发呈显著负相关（P<0.01），完全相关系数风速（0.624）>相对湿度（0.418）。灰色关联度结果显示风速（0.708）>相对湿度（0.626）>0.5，则两者与蒸发量均为较高关联，风速关联度最高，表明风速对蒸发量影响的最大，与相关分析结果相一致。

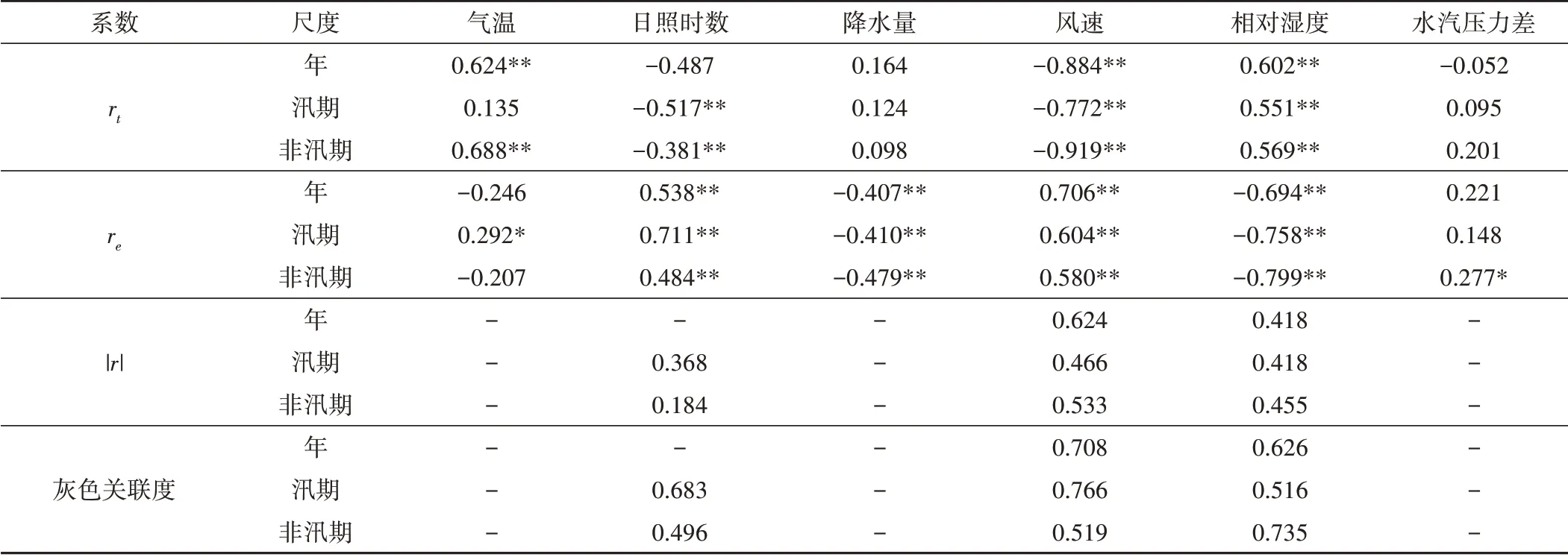
表2 水面蒸发与各气象要素Pearson相关系数、完全相关系数及灰色关联度Tab.2 Pearson correlation coefficient,perfect correlation coefficient and gray correlation degree between evaporation and meteorological elements

汛期与非汛期相对湿度，风速，日照时数与蒸发均显著相关（P<0.01）；汛期灰色关联度均在0.5～0.85 范围内，属较高关联；而非汛期日照时数灰色关联度为0.496，小于0.5，属低关联。

上述结果表明：年际与非汛期蒸发量主要影响因子为风速、相对湿度；而汛期蒸发量主要影响因子为风速、相对湿度、日照时数。

3.4 “蒸发悖论”成因分析

为进一步研究该区“蒸发悖论”成因，以水面蒸发量为因变量，以风速、相对湿度、日照时数为自变量，分别建立年际与（非）汛期多元回归线性模型，由表3可见，年际、汛期、非汛期模型拟合调整R2值分别为0.604、0.684、0.658，即自变量可代表因变量约60%、68%、66%的变化。

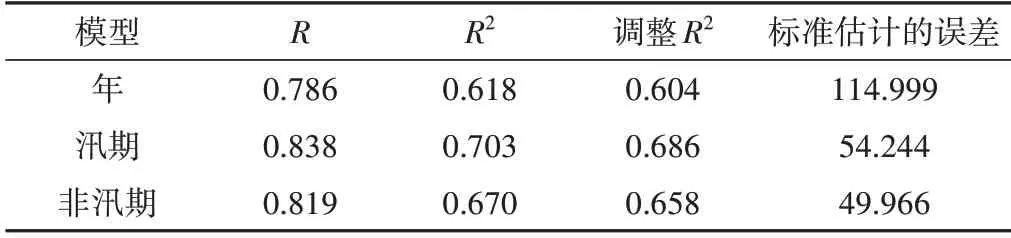
表3 复相关系数变化情况Tab.3 The change of complex correlation coefficient

年尺度与（非）汛期蒸发量与主要影响要素多元回归结果见表4，表中B代表蒸发影响要素的回归系数，结合本文3.3相关分析结果，设置年际、非汛期预测变量：(常量),风速,相对湿度；汛期预测变量：(常量)风速,相对湿度,日照时数。

由表4可知，回归结果具有显著性。回归方程分别为：

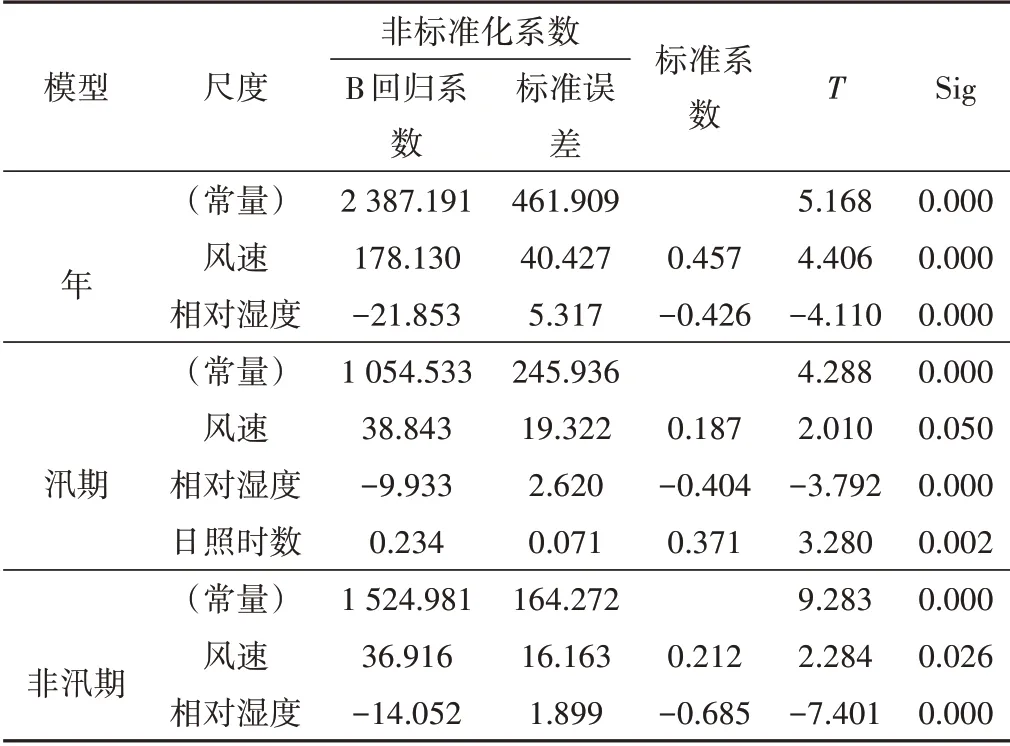
表4 蒸发量主要影响要素偏回归系数及其显著性Tab.4 The partial regression coefficient and its significance of the main factors affecting evaporation

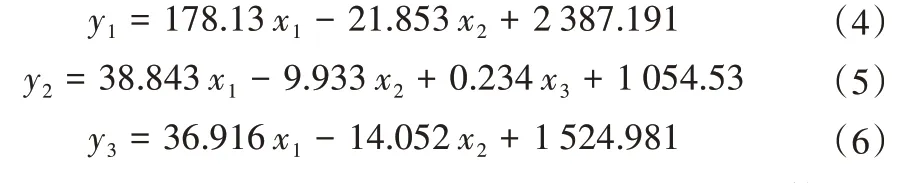
式中：x1为平均风速；x2为平均相对湿度；x3为日照时数；y1为年尺度拟合蒸发量；y2为汛期拟合蒸发量；y3为非汛期拟合蒸发量。

根据公式(4)～(6)计算得到各尺度蒸发量的模拟值，以蒸发皿实测值为横坐标、相应模拟值为纵坐标绘制散点图见图3，由此检验两者拟合关系。

由图3(a)可见，年尺度实测值与其相对应模拟值大致均匀分布在y=x直线两侧。年际回归相对误差为0.04%～32.45%，平均相对误差为6.54%，相对误差绝对值在20%以内归为合格，则合格率为96%。

由图3(b)与图3(c)可见，汛期与非汛期实测值与其相对应模拟值大致均匀分布在y=x 直线两侧。汛期回归相对误差为0.13%～55.18%，平均相对误差为7.64%，合格率为96%；非汛期回归相对误差为0.12%～21.42%，平均相对误差为7.21%，合格率为98%。

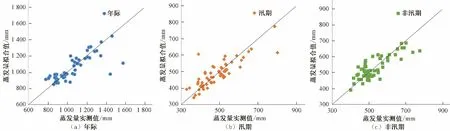
图3 年际、汛期和非汛期实测与模拟值关系图Fig.3 Relationships between measured and simulated values in interannual,flood season and non-flood season

上述结果表明，回归方程拟合较好，可用其分析各影响因子对蒸发皿蒸发量贡献率。

水面蒸发量M-K 突变检验如图4所示，UF与UB两曲线交点不在临界线内，没有发生显著突变。UF曲线1989年后超出临界值范围，且UF值均小于0，该年后蒸发量存在显著的下降趋势。

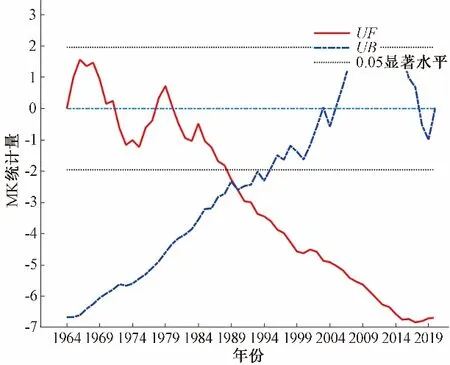
图4 水面蒸发量M-K突变检验Fig.4 M-K mutation test of water surface evaporation

蒸发量累积距平值于20世纪80年代达到峰值，且1989年后呈显著下降趋势，因此可将1964-1989年作为基准期，分析1990-2020各影响因子对于蒸发量相应变化量及贡献程度，各因子贡献率结果见表5。

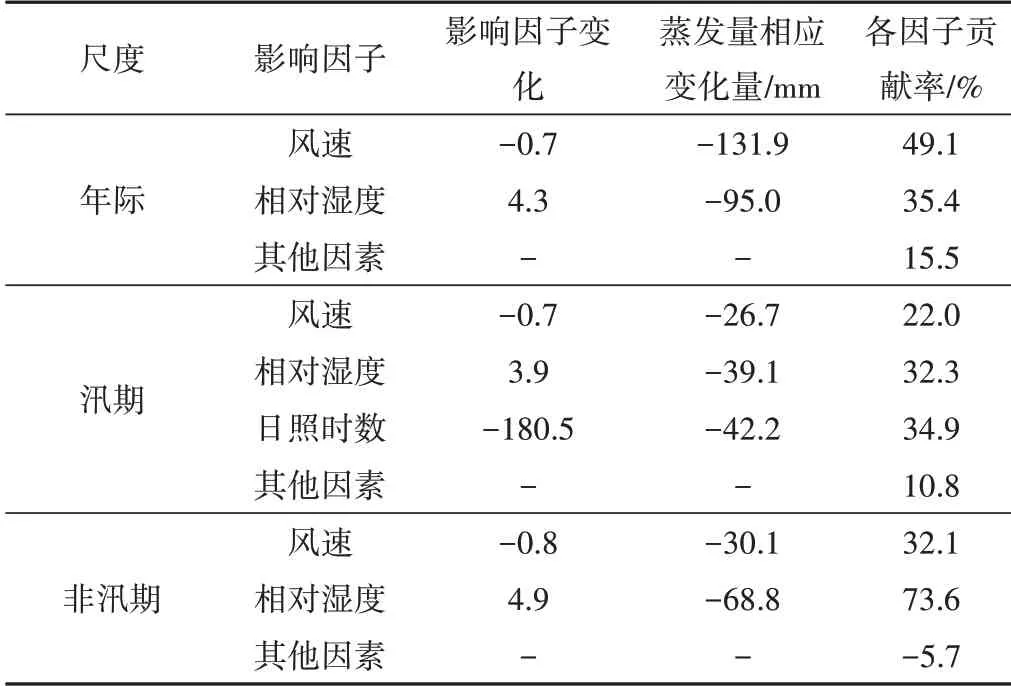
表5 各因子对蒸发量的影响量及贡献率Tab.5 The influence amount and contribution rate of each factor on evaporation

年尺度1990年后蒸发量较基准期下降268.5 mm，风速下降0.7 m/s，导致蒸发量相应减少131.9 mm；相对湿度增加4.3%，导致蒸发量相应减少95 mm。两者对蒸发量下降的贡献率分别为49.1%与35.4%，其他贡献率为15.5%。

汛期蒸发量较基准期下降121.1 mm，风速下降0.7 m/s，相对湿度增加3.9%，日照时数减少180.5 h，蒸发量分别相应减少26.7、39.1、42.2 mm，故风速、相对湿度、日照时数贡献率分别为22.0%、32.3%、34.9%，其他贡献率为10.8%。

非汛期蒸发量较基准期下降93.5 mm，其中风速下降0.8 m/s，导致蒸发量相应减少30.1 mm；相对湿度增加4.9%，导致蒸发量相应减少68.8 mm。两者对于蒸发量量下降的贡献率分别为32.1%与73.6%，其他贡献率为-5.7%。

该地区“蒸发悖论”主要成因是风速下降、相对湿度的增加以及日照时数的减少，该结论与王怡宁[12]、李秀[13]、陈伏龙[22]等研究成果具有一致性。

4 结 语

（1）五道沟地区近57年平均气温上升了0.27 ℃/10a，而蒸发皿实测蒸发量以85.8 mm/10a 速率下降，该地区存在“蒸发悖论”现象。该地区存在明显“蒸发悖论”现象；汛期、非汛期气温分别以0.05、0.27 ℃/10a 上升，蒸发以41.49、30.39 mm/10a下降；汛期“蒸发悖论”规律更具显著性，排序为汛期＞年＞非汛期。

（2）近5 个年代中，20世纪80年代气温上升0.37 ℃/10a，蒸发量下降122.67 mm/10a；该时段气温上升幅度最小，且蒸发量下降幅度最大，“蒸发悖论”规律最显著。21世纪以来，较20世纪末气温变幅增大，蒸发量变幅减小，悖论现象较不明显。

（3）各气象要素趋势分析结果表明：蒸发量各尺度均呈显著下降趋势；气温年尺度与非汛期呈显著上升趋势，汛期无明显变化趋势；降雨量以14.06 mm/10a 速率上升但变化不显著；相对湿度以1.29%/10a 速率显著上升；日照时数与风速气候呈显著下降趋势，气候倾向率分别为-102.76 h/10a 与-0.25 m·s-1/10a；水汽压力差无明显变化趋势，气候倾向率为-0.03 mb/10a。

（4）该地区“蒸发悖论”主要成因是风速下降、相对湿度的增加以及日照时数的减少。与1964-1989年基准期相比，1990-2020年各影响因子对蒸发量下降的贡献率为：年尺度上，风速（49.1%） ＞相对湿度（35.4%）；汛期日照时数（34.9%）＞相对湿度（32.3%）＞风速（22.0%）；非汛期相对湿度（73.6%）＞风速（32.1%）。

本文分析淮北平原年尺度、汛期、非汛期及年代多尺度蒸发量下降差异性及其成因，仅考虑气象要素对蒸发量的影响。考虑多站点、多影响因素，在更大区域上分析“蒸发悖论”及成因有待进一步研究。