BF-850B立式高速数控机床精度检测及误差补偿研究

杨秀芝，查吉利，徐绍勇，王兴东，蒋宇辉

(1.湖北理工学院智能输送技术与装备湖北省重点实验室，湖北黄石 435003；2.武汉科技大学冶金装备及其控制省部共建教育部重点实验室，湖北武汉 430081)

0 前言

为迎接中国制造2025的到来，国内数控机床数量和质量均呈现突飞猛进势头，但与欧美日所产机床相比精度等方面还存在差距。特别是随着计算机技术、微电子的发展，数控机床正加速进步，以便满足各方用户更多需求。其中对数控机床定位精度的检测、控制与补偿已成为国际机床展上各国机床制造商展示其机床核心技术指标和焦点[1]。本文作者针对所研究的BF-850B立式高速高精度线轨数控机床，提出了激光干涉仪与循圆检测共同补偿策略，对机床精度进行补偿研究。研究结果表明：该补偿方式可以很好地弥补工作台及其他部件带来的人工或加工误差，并根据计算机反馈的信息进行补偿，效果较好。

1 定位精度的检测方法

BF-850B立式数控机床主要运用于汽车零部件、家电模具和小型模具架加工，机床主要包括X、Y、Z三个移动轴以及主轴和刀库两个旋转轴。

此检测方法分为两部分：第一部分为激光干涉仪，进行三轴精度检测及误差补偿；第二部分为球杆仪，进行循圆检测及误差补偿。搭建的实验平台如图1所示。

图1 基于BF-850B机床的实验平台

1.1 波长补偿

线性定位测量精度取决于激光波长，激光波长测量精度不仅和激光稳频精度有关，还与环境参数如气压、相对湿度和气温有关[1]，所以在对机床进行精度检测及补偿之前需对激光进行波长补偿分析。

本文作者所用激光干涉仪具有激光波长自动补偿系统，这样，可自动调整激光波长读数。

1.2 三轴精度检测方法及原理

1.2.1 定位精度检测方法

数控机床静态补偿的原理是在数控系统无补偿的情况下，将测量行程N等分，测出目标位置的误差值。单向补偿方式的补偿值参照正向误差值求得。增量型补偿是取相邻两点位置偏差的绝对值作为补偿量，输入到数控系统参数中。待误差补偿生效后，数控系统实现误差补偿功能。

1.2.2 定位精度检测原理

实验中要对线性测量进行设定，使用随附的两个外螺钉将其中的一个线性反射镜安装在分光镜上。这个组合装置称为“线性干涉镜”，它形成激光光束的参考光路。线性干涉镜放置在激光头和线性反射镜之间的光路上，如图2所示。

图1为此次测试平台，采用线性角锥反射镜系统[1-2]，系统硬件配置如图3所示。其过程如下：(1)激光头发出的光被分光镜 A分成两束光；(2)大约一半激光被射到固定角锥反射镜 B上，形成参考光束；另一半激光射到移动角锥反射镜C上，形成测量光束。

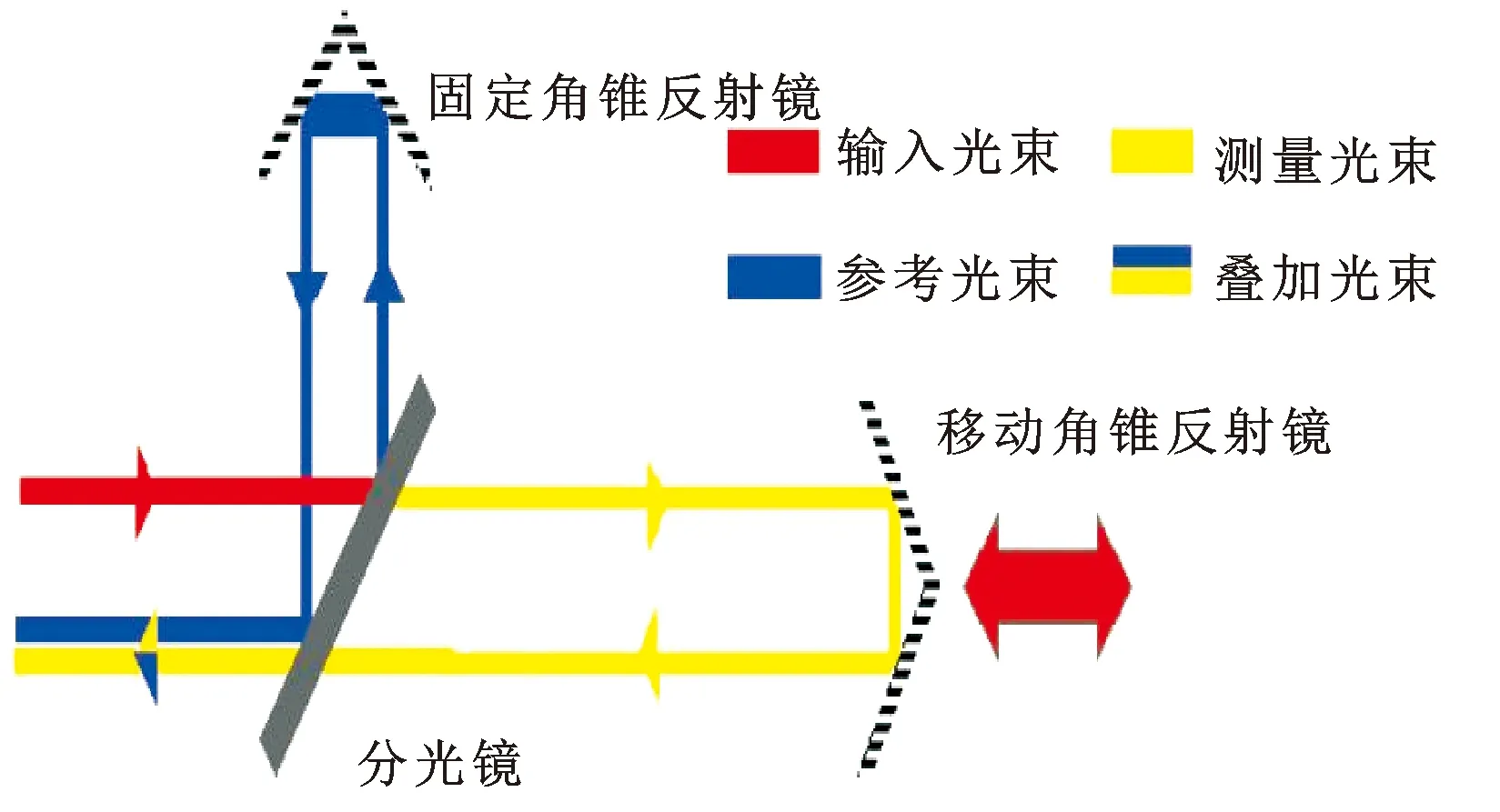
图2 线性干涉原理示意

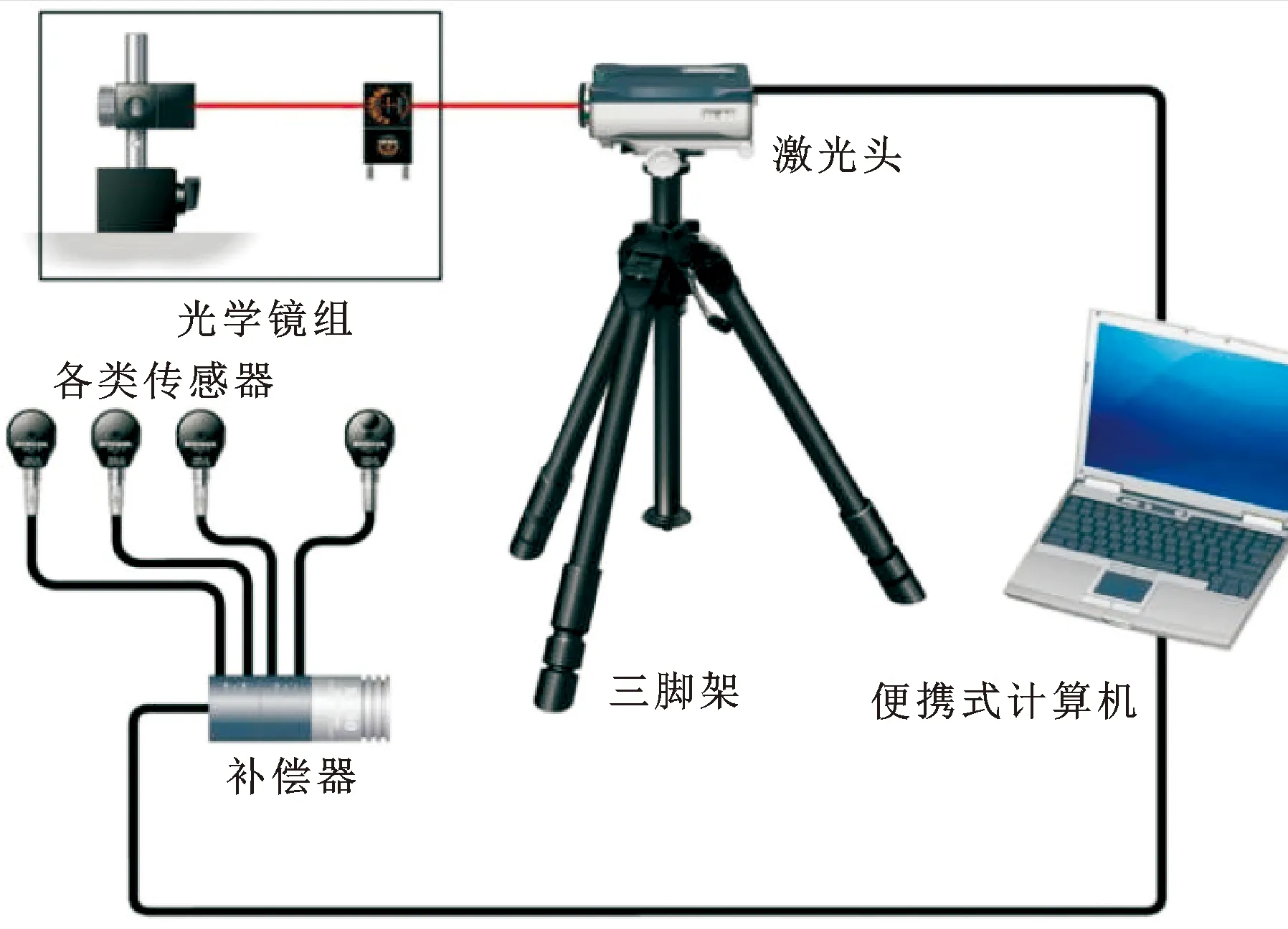
图3 实验基本线性测量硬件配置

根据国际标准ISO 230-2 1997中关于机床定位精度和重复定位精度的评定方法，可得单向定位精度的数学模型的系列公式[3]如下：

(1)

(2)

单向重复定位精度为

Ri↑=max[4si↑]

(3)

Ri↓=max[4si↓]

(4)

(5)

(6)

式中：j为循环次数；Pi为第i个测量点序的理论位置；Pij、xij分别为第j次循环下第i个测量点序的实际位置和位置偏差。按上述数据处理方法，将采集数据输入数控机床精度检测系统，得到误差补偿数据。

1.3 检测实例分析

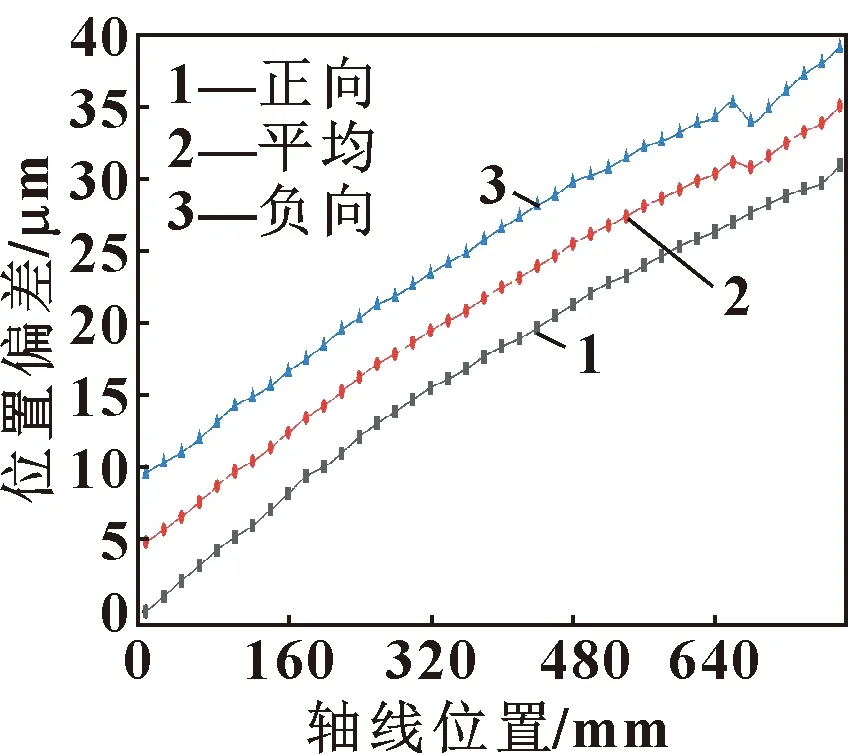
图4 x轴未补偿时位置偏差曲线

文中研究以BF-850B立式高速高精度线轨机床搭建测试平台，采用激光干涉仪检测x轴定位精度，测量方法为等间距测量法，螺距误差补偿方式为单向增量型补偿。根据采集到的数据进行误差分析，然后进行误差补偿。数据采集方法：将机器沿着测试轴移动到若干个不同位置，然后测量机器的误差。也可以采用编写零件程序的方法，将被测物从一个目标位置移到下一个目标位置，并在每个目标位置暂停几秒钟，在每次暂停过程中进行测量[4]。通过直接对数控机床进行精度检测，得到未补偿时的定位精度曲线如图4所示。可知：补偿前平均位置偏差为0.030 2 mm。系统偏差为0.039 1 mm，定位精度为0.040 5 mm，且曲线呈逐级递增趋势，说明x轴运动误差呈升高趋势，因此需要进行误差补偿。

将补偿间隔设为20 mm，在补偿起点为0、终点为780 mm处进行采集，数据设置如图5所示；此处分别采用同一系数对所有行程区间内的点位进行一次性线补偿和将全测量行程根据其误差特性差别采用若干个细分区间采用不同系数分别进行补偿的多段式线性补偿。并基于Python软件的pycharm集成开发环境构建sklearn线性拟合模型，将得到的误差补偿数据输入至数控机床控制系统，然后按照补偿前的方式继续操作后得到补偿后位置偏差如图6所示。

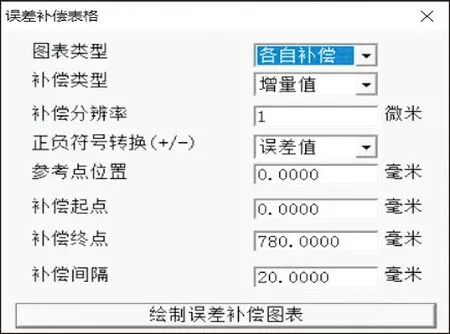
图5 误差补偿调整图

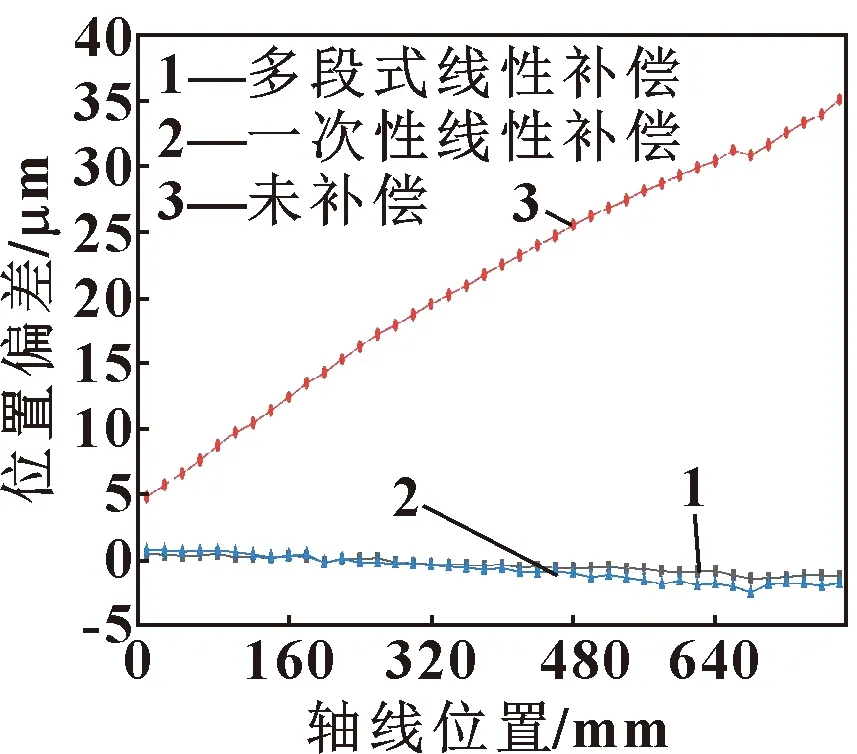
图6 补偿后x轴位置偏差曲线

由图6可知：补偿前均偏差范围为0.003 2 mm，系统偏差为0.004 2 mm，定位精度为0.005 6 mm，且曲线图偏差范围在很小范围内波动，x轴运动轨迹已趋于平稳，说明误差已得到很好的补偿。通过图6导出补偿后误差补偿值，分析前后两个均值补偿数值并对它们分别做均值计算得:

补偿前均值为

补偿后均值为

由此可知：补偿后的均值更趋近于0，这证明数控机床的稳定性能得到了较好的提升，从而使得机床精度明显提升。

对比图4、图6可以看出：数控机床的x轴精度由补偿前的均偏差范围0.030 2 mm提高到补偿后的均偏差范围0.003 2 mm。定位精度和重复定位精度均有不同程度的提升。由此可知，运用激光干涉仪进行误差补偿，该补偿策略原理正确、效果显著。

2 球杆仪下循圆检测

运用球杆仪检验工作台面的水平精度(以xy轴垂直度为例)，补偿前如图7所示。可知：工作台面的水平精度为0.005 3 mm，且上下左右4个方位的差值明显，需要对工作台的精度进行补偿，就必须对工作台作真圆度分析。通过参数修改和仿真分析，得到误差补偿后的结果如图8所示。工作台面的水平精度为0.001 0 mm，且上下左右4个方位的峰值明显减小。由此证明，运用该方法对工作台面进行真圆度分析，该补偿方法原理正确、效果明显。

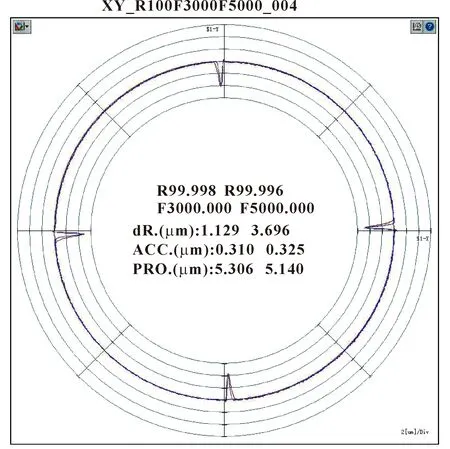
图7 补偿前曲线

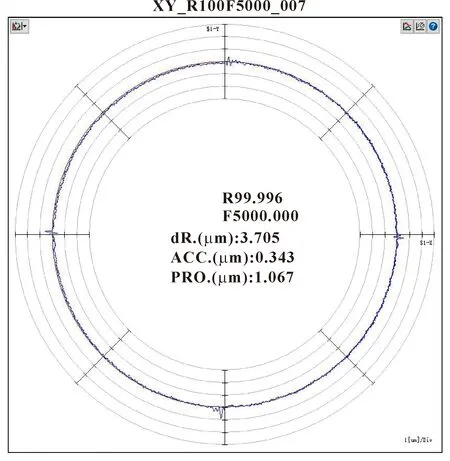
图8 补偿后曲线

3 结语

通过激光干涉仪对选定机床进行三轴定位精度检测，并对反向间隙误差和丝杠螺距误差进行补偿，同时结合球杆仪进行循圆检测及误差补偿。这两种测试手段的结合大大提升了数控机床的精度水平；实验中通过多次实验确保了测量数据的可靠性。可见，此方法对数控机床精度检测与误差补偿具有时效性和通用性，可以大大缩短检测周期，降低开发成本。