电液位置伺服系统的自适应抗饱和控制

鄂东辰，路时雨，刘超强，蔡玉强，张立杰

(1.华北理工大学机械工程学院，河北唐山 063210；2.燕山大学河北省重型机械流体动力传输与控制重点实验室，河北秦皇岛 066004；3.燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004)

0 前言

电液伺服系统具有功率密度大、响应速度快等优点，被广泛应用于工程机械、军工和航空航天等领域。由于电液伺服系统具有非线性和参数不确定性等特点[1]，给控制器的设计造成了很大困难。为达到较好的控制效果，学者们对其进行了大量的研究。

阀控缸电液位置伺服系统控制方法分为基于模型的方法[2-3]和基于误差反馈的方法[4-5]，前者理论性强，适用于非线性控制对象，后者原理简单，不需要建立被控对象的数学模型，但其本质为线性控制方法，不适用于非线性被控对象。因此，基于模型的方法为电液伺服系统控制策略的主要研究方向。针对模型参数不确定问题，学者们提出了多种鲁棒控制算法，例如滑模控制[6-7]、自适应控制[8-10]和自抗扰控制[11-12]等。滑模控制是将状态变量限制在滑模面上，减小参数变化对控制精度的影响。赵清亮等[13]应用滑模控制，实现金刚石超精密加工。吴宝举等[14]应用滑模方法控制水下机器人。自适应控制是根据系统输入和输出自适应调整模型的参数，保证控制器的有效性。程冲等人[15]应用自适应控制，实现了发电机转子惯量的调节。侯忠生等[16]应用无模型自适应方法，实现了车辆的自动泊车。自抗扰控制是1998年我国学者韩京清[17]提出的，通过扩展观测器估计系统的干扰和未知因素，再将估计值加入到控制器中以补偿干扰和未知因素的影响，很好地解决了系统参数不确定问题。邱建琪和留若宸[18]提出改进自抗扰控制方法，实现电机的位置调节。

以上的鲁棒控制策略中没有考虑系统输入饱和问题。在生产实际中，饱和现象普遍存在[19-20]，如伺服阀的控制电压被限制在±10 V之间，当控制量超出这个范围时阀芯位移不再随输入电压的增加而增大，即发生输入饱和。这时伺服阀不能根据控制信号准确地调节进入液压缸的流量，导致液压缸位移跟踪精度降低。对此，本文作者针对具有输入饱和限制和不确定性的阀控缸电液伺服系统提出自适应抗饱和控制策略，在反步法的设计框架下通过加入自适应与抗饱和算法解决参数不确定和输入饱和问题，并且通过粒子群算法优化控制器的参数。根据Lyapunov理论证明系统渐进稳定。通过仿真对比，验证该控制策略的优越性。

1 阀控缸系统建模

阀控缸电液位置伺服系统如图1所示。系统主要包括定量泵1、溢流阀2、伺服阀3和双活塞杆液压缸4。根据伺服阀的流量方程、液压缸流量连续性方程和液压缸活塞受力平衡方程建立系统的数学模型。

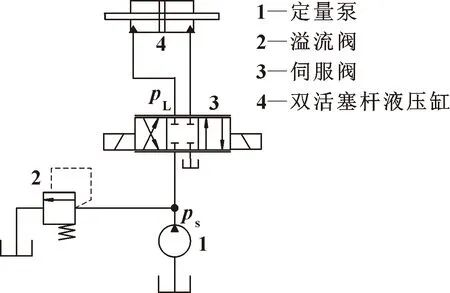
图1 阀控缸电液位置伺服系统

伺服阀流量方程为

(1)

式中：QL为流经伺服阀的流量；Cd为伺服阀口的流量系数；w为伺服阀口的面积梯度；xv为伺服阀阀芯位移；ps为伺服阀入口压力；pL为伺服阀出口压力；ρ为液压油密度。

液压缸流量连续性方程为

(2)

式中：Ap为液压缸活塞的作用面积；Ct为液压缸内泄漏系数；V为液压缸进油腔的容积；βe为油液的体积弹性模量。

液压缸活塞受力平衡方程为

(3)

式中：mt为活塞质量；Bp为活塞与缸筒内壁之间摩擦力的黏性阻尼系数；k为负载弹簧的弹性刚度；FL为外负载力。

伺服放大器等效为比例环节。伺服阀输入电流与阀芯位移之间的关系也等效为比例环节，则有:

kp=i/u

(4)

ksv=xv/i

(5)

式中：kp为伺服阀放大器的放大系数；ksv为伺服阀阀芯位移与输入电流i的比例系数；u为控制器输出电压。

(6)

y=x1

(7)

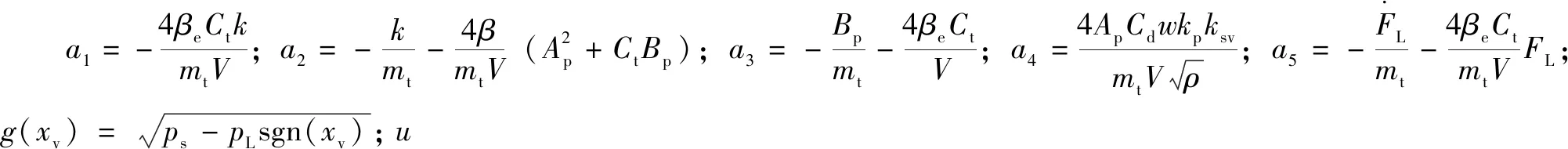
上式中外负载FL、黏性阻尼系数Bp和内泄漏系数Ct通常是不确定的，因此需要对它们进行在线自适应调整，使其更加准确地体现系统的工作状态，为控制器的设计奠定基础。

2 抗饱和控制器设计

在反步法非线性控制器的设计思想下，针对输入饱和与参数不确定问题，设计自适应抗饱和控制器。反步法是一种基于李亚普诺夫稳定性理论的反向递推设计方法，其适用于高阶非线性系统。由公式(6)可知，系统为3阶非线性微分方程组，针对每一个方程设计一个控制器。

2.1 位移环控制器设计

定义液压缸活塞位移的跟踪误差为

e1=x1-x1d

(8)

式中：x1d为设定的位移轨迹；x1为系统状态的实际值。如果e1等于零则x1完全准确地跟踪了x1d。

设Lyapunov函数为

(9)

则有：

(10)

x2作为位移环的控制量，根据Lyapunov稳定性理论设计x2的期望值，即位移环的虚拟控制量x2d为

(11)

2.2 速度环控制器设计

定义液压缸活塞速度跟踪误差为

e2=x2-x2d

(12)

将公式(11)(12)代入式(10)中得:

(13)

设第二个Lyapunov函数为

(14)

将公式(6)(12)(13)代入上式并求导得：

(15)

x3作为速度环的控制量，根据Lyapunov稳定性理论设计x3的期望值，即速度环的虚拟控制量x3d为

(16)

2.3 未考虑输入饱和时加速度环的控制器设计

定义液压缸活塞的加速度跟踪误差为

e3=x3-x3d

(17)

将公式(16)(17)代入式(15)中得：

(18)

设第三个Lyapunov函数为

(19)

将式(6)(18)代入上式得:

(20)

u作为加速度环的控制量，也是整个系统的控制输入。根据Lyapunov稳定性理论设计的u为

(21)

2.4 抗饱和加速度环的控制器设计

在控制器的设计过程中考虑到伺服阀的输入饱和限制，重新定义加速度跟踪误差，使其不仅包含由于控制算法导致的误差并且包含由于控制器输入饱和限制导致的误差，其计算公式为

(22)

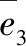
(23)

式中：u0为伺服阀输入的理想值。u为受饱和函数约束后的实际控制量,u=sat(u0,uL,uU)，其中sat为饱和函数，其计算公式为

(24)

式中：uL和uU分别代表伺服阀输入的下极限值和上极限值，uL=-10 V、uU=10 V。

由公式(6)(22)得：

kx3χx3-a4g(xv)(u-u0)

(25)

定义新的第三个Lyapunov函数为

(26)

则：

(27)

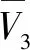
(28)

式中：η为鲁棒控制项，将在稳定性分析中给出。

3 系统稳定性分析和鲁棒控制项设计

3.1 未考虑输入饱和时的系统稳定性分析

根据公式(19)可得V3为正定函数。将式(21)代入式(20)中得:

(29)

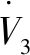
3.2 抗饱和算法的系统稳定性分析与鲁棒控制项设计

(30)

令

(31)

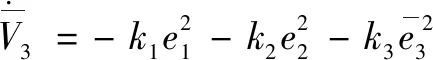
4 模型参数自适应

(32)

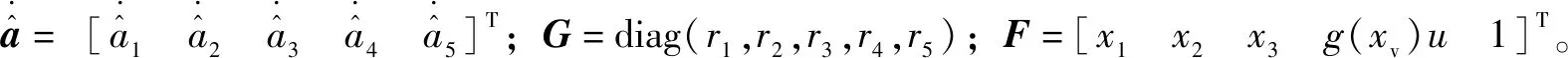
将参数的自适应估计值代替控制器(28)中的参数，并将鲁棒控制项代入，得到自适应抗饱和控制器为

(33)

加速度环的自适应抗饱和控制策略的结构框图如图2所示。

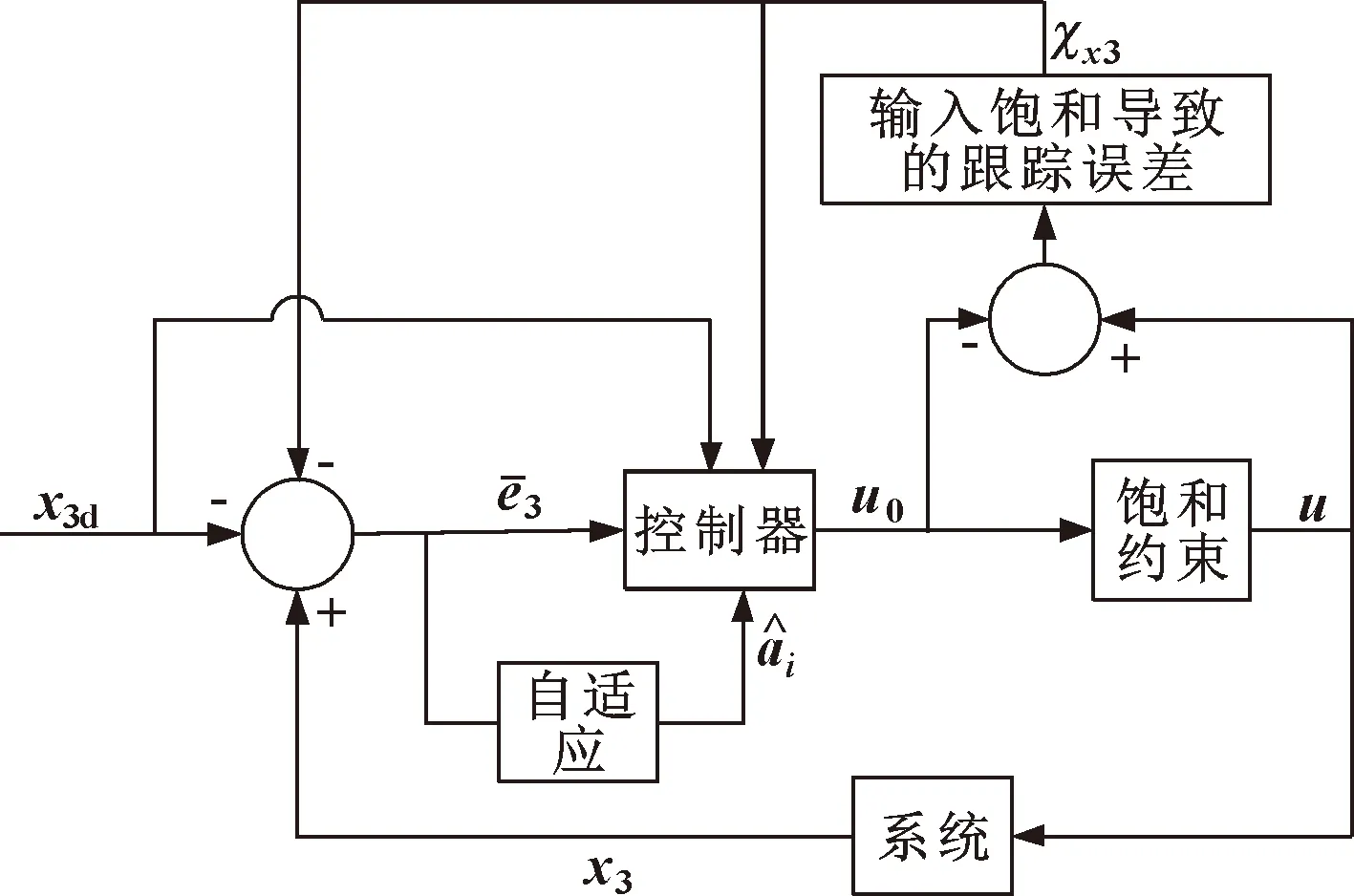
图2 自适应抗饱和结构框图

5 控制器参数优化

自适应抗饱和控制器的参数包括k1、k2、k3和kx3，这些参数影响了系统的收敛速度和跟踪精度。在控制器的设计过程中，通常根据经验确定这些参数，但该方法受到设计者主观经验的影响，效率较低。对此，采用粒子群算法优化控制器的参数。粒子群算法是一种群体智能全局搜索算法，它在规划搜索路径过程中不仅参照个体本身的最优信息，同时也参照整个群体的最优信息，使其能够快速地搜索到全局最优解。

针对前文中的控制器，定义粒子群优化的目标函数为

(34)

式中：n为仿真步数。

粒子的速度更新和位置更新计算公式分别为

(35)

(36)

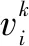
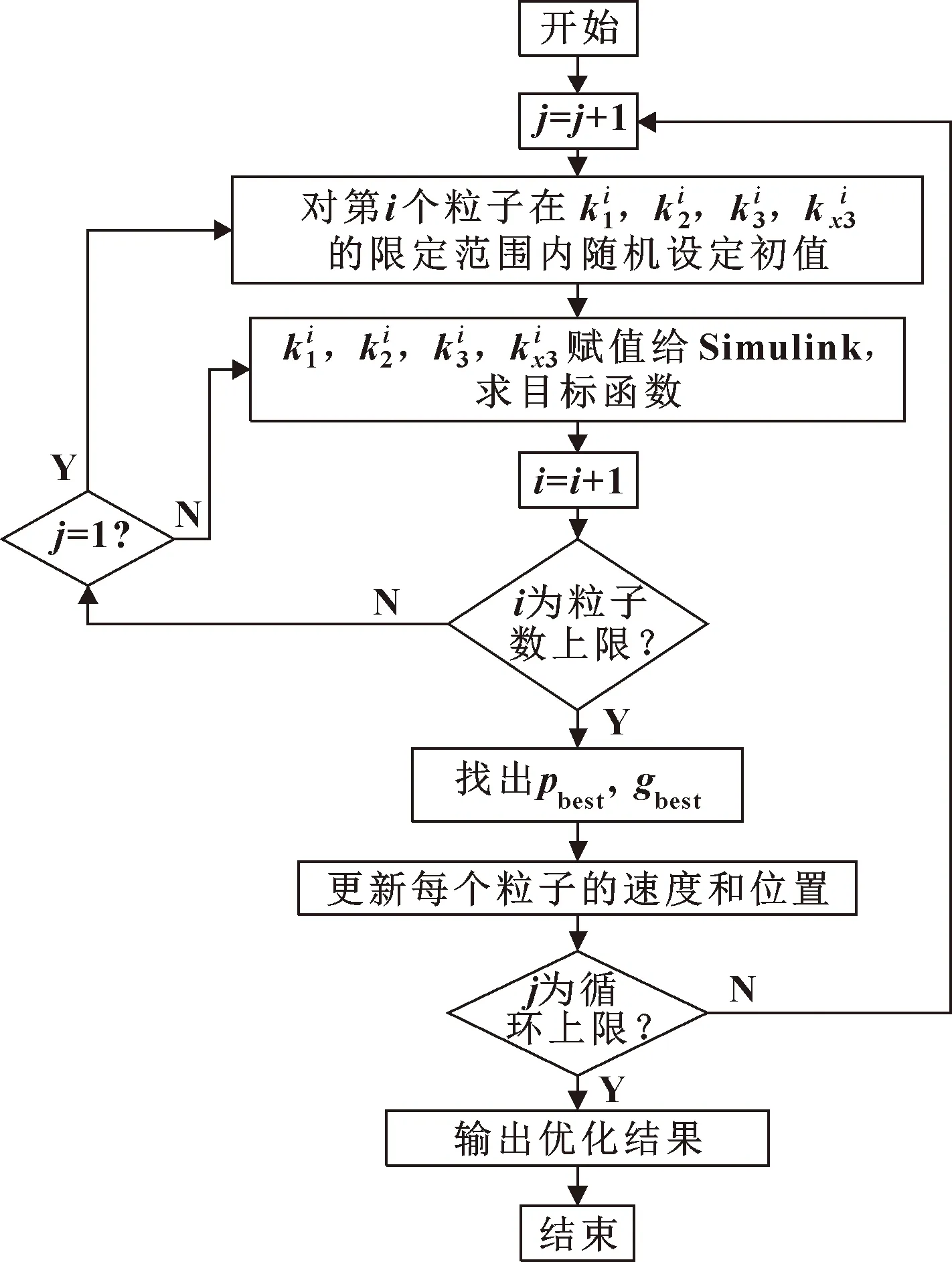
图3 粒子群优化算法流程

6 仿真结果与分析

通过Simulink仿真验证算法的有效性。根据阀控缸系统的实际工况设定仿真的模型参数如表1所示。位移环积分器的初始条件设为0.8，速度环和加速度环积分器的初始条件设为0。自适应参数设定为ri=1 (i=1～3)、r4=1×10-13、r5=1。仿真时长设为20 s。采用obe45微分方程数值求解算法。

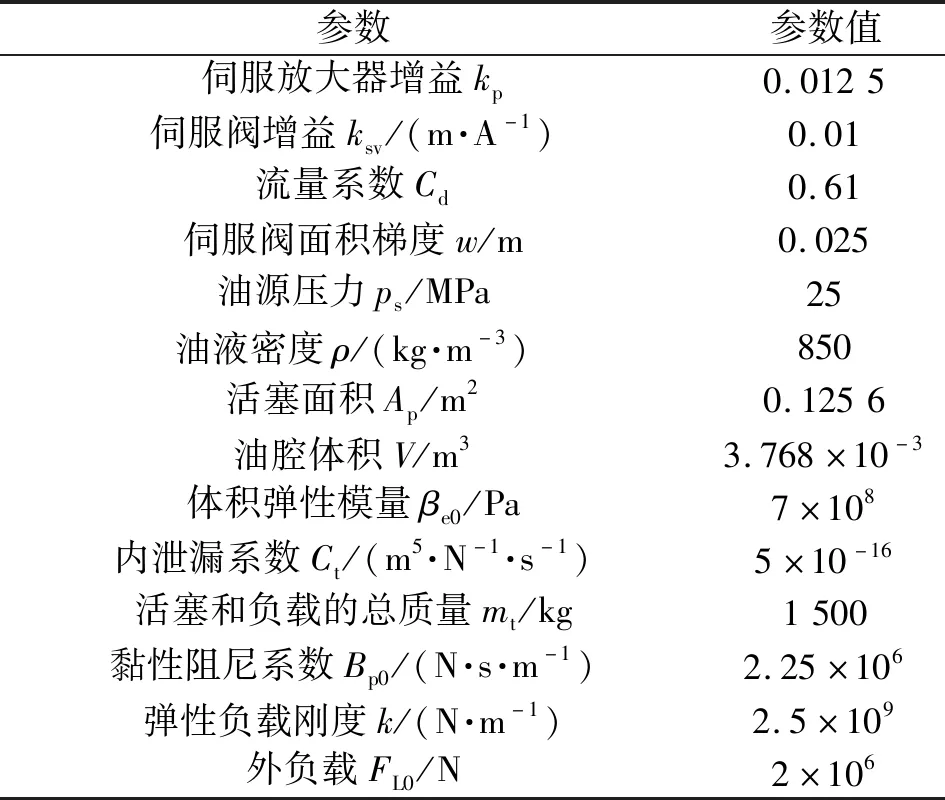
表1 仿真模型的参数

设定系统的位移跟踪目标为

x1d=1+0.5sin2πt

式中：t运行为时间。

在仿真过程中设定FL、Bp和βe按照公式(37)(38)(39)规律变化，以模拟系统参数的不确定性。

FL=FL0+0.09FL0sin(2π2t)

(37)

Bp=Bp0+0.05Bp0sin(2π2t)

(38)

βe=βe0+βe0×10-6sin(2π2t)

(39)

在粒子群优化算法中，设定循环次数为50次，粒子个数为30个。学习因子c1=c2=2，惯性因子ω=0.6，粒子最大运动速度vmax=500。利用MATLAB求解得出50次循环的目标函数如图4所示。控制器参数的寻优过程如图5所示。当循环次数大于40以后,目标函数和优化参数基本稳定，得出k1=4 818、k2=7 398、k3=12 849、kx3=3 377，再将这些优化结果代入Simulink模型中。

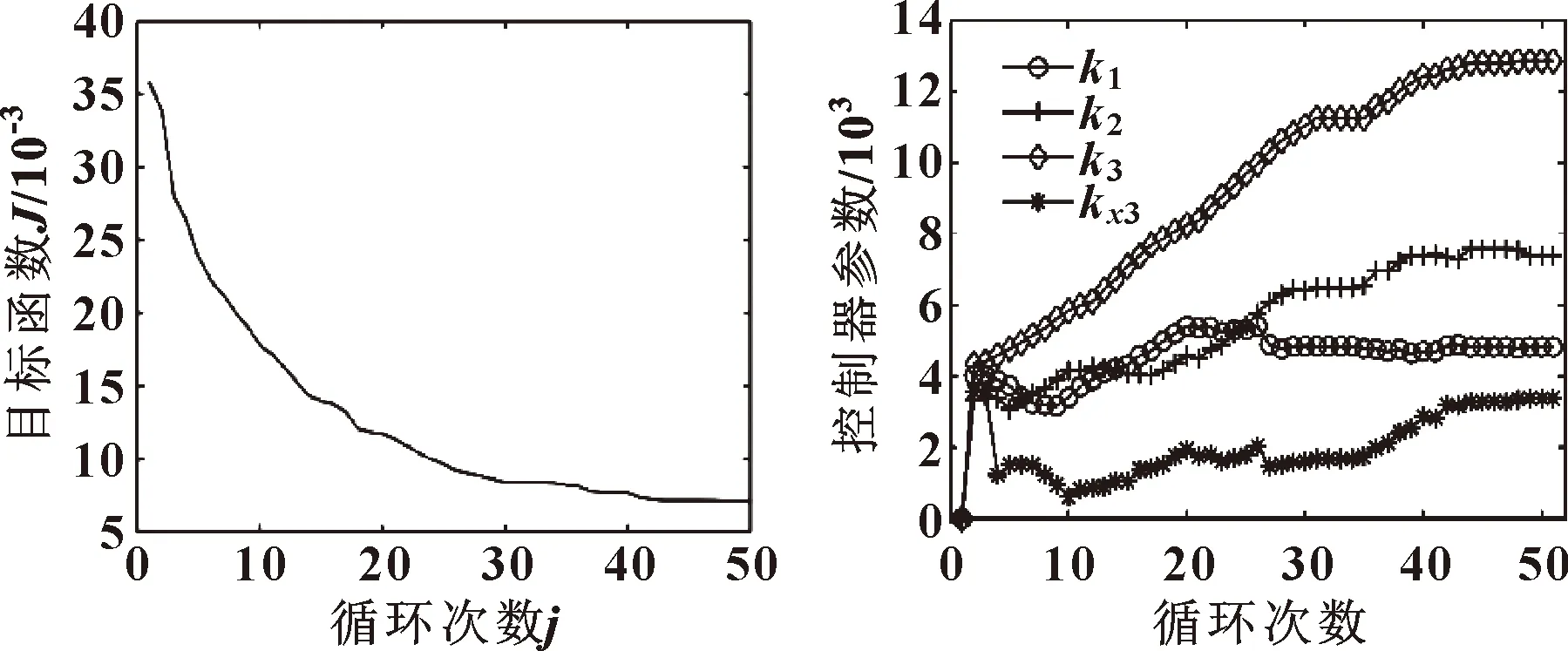
图4 优化过程的目标函数 图5 优化过程的控制器参数

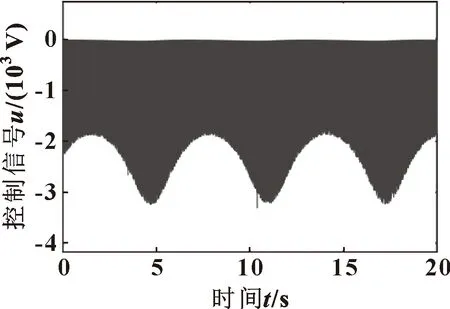
图6 无饱和限制的控制信号

当控制信号没有饱和限制时(u=u0)，控制信号和位移跟踪曲线分别如图6、7所示。可知：u0在-3 000～0 V之间波动；在该控制信号下位移具有较高的跟踪精度，最大跟踪误差为2.7×10-5mm，但是u0远超出了伺服阀可接受的电压范围，不符合真实工况。在相同的仿真条件下对控制信号进行饱和限制得到的理想控制信号如图8所示。由于饱和的限制使跟踪误差增加导致u0幅值急剧增大，使实际控制信号u在uL～uU之间往复波动，得出的位移跟踪曲线如图9所示。可知：由于输入饱和的影响使跟踪精度降低，最大跟踪误差达到-0.7 mm。

当采用文中提出的抗饱和策略后，在相同的仿真条件下得出的控制信号如图10所示，相对于无饱和限制的控制信号的幅值明显减小，在稳态阶段控制信号的幅值在±10 V之间，避免了输入饱和。其跟踪曲线如图11所示。在稳态阶段最大跟踪误差为5.8×10-6mm，相对无抗饱和方法误差显著减小，验证了抗饱和控制策略的有效性。

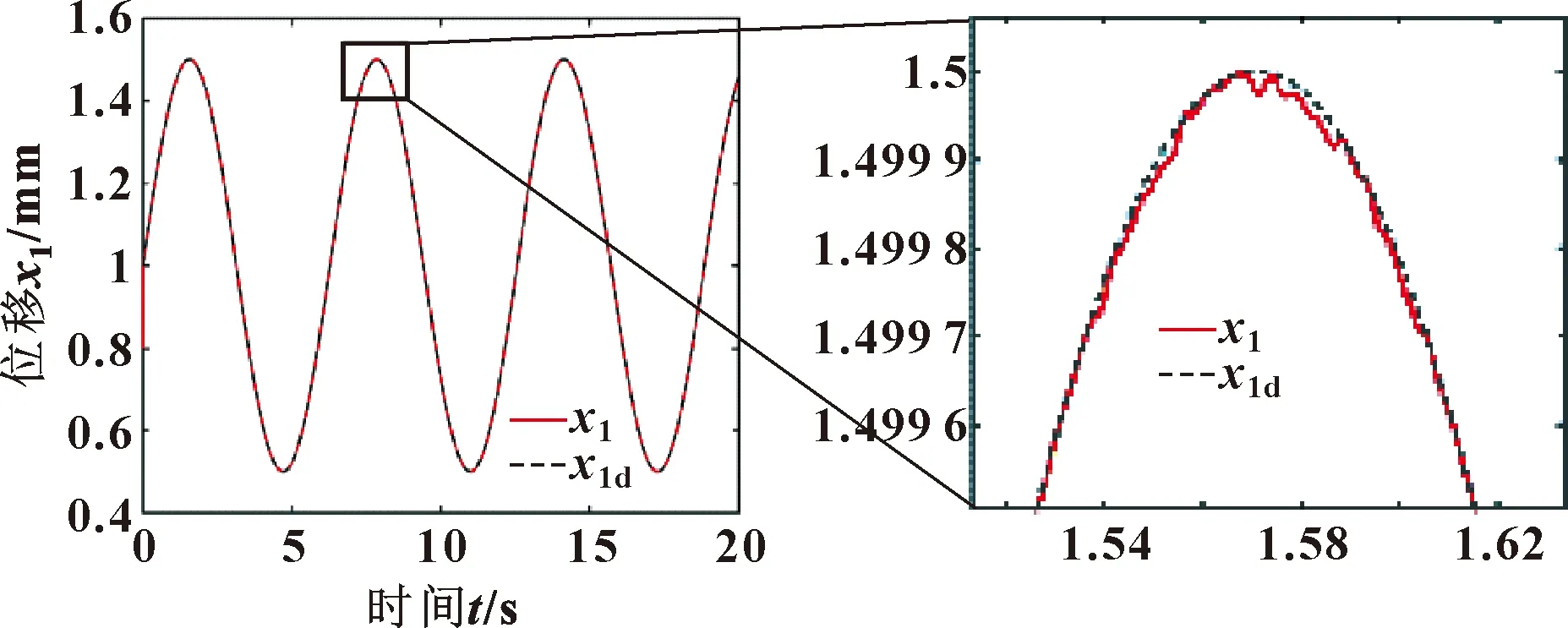
图7 无饱和限制的位移跟踪

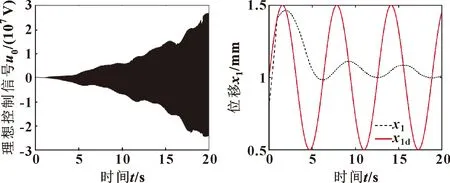
图8 有饱和限制的理想控制信号 图9 有饱和限制的位移跟踪

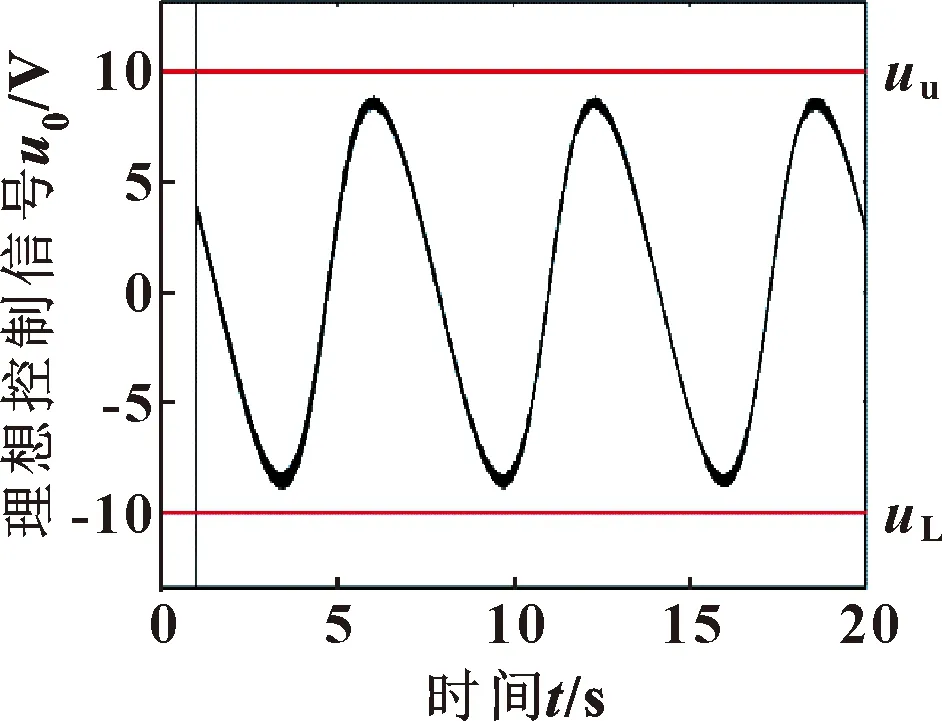
图10 抗饱和控制信号

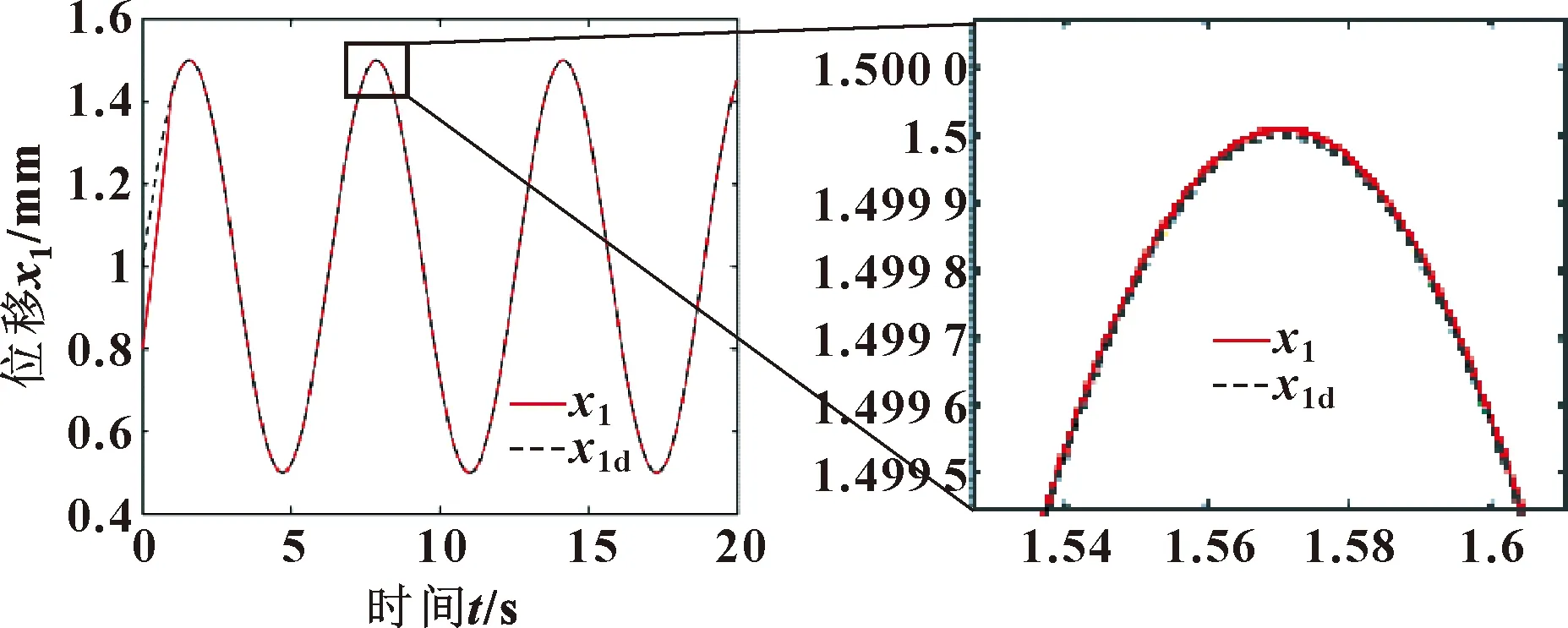
图11 抗饱和控制的位移跟踪

7 结论

(1)针对电液位置伺服系统的输入饱和问题在自适应反步法的基础上提出抗饱和控制策略，将输入饱和导致的误差加入到Lyapunov函数中，并基于该函数设计控制器，使伺服阀的控制信号减小到可接受的输入范围内，避免输入饱和。

(2)针对控制器参数的选取问题，通过粒子群搜索方法优化控制器的参数。

(3)仿真结果表明：该控制策略在参数不确定且具有输入饱和限制的条件下位移最大跟踪误差为5.8×10-6mm，与无抗饱和算法误差相比显著减小。研究成果为参数不确定、输入饱和限制的系统控制器设计提供了参考。