定模动辊机电系统动力学智能优化方法

王鹏远

(北方工业大学机械与材料工程学院，北京 100144)

0 前言

将高强钢板材通过渐进成型方式制成变截面构件，在轻量化工程应用中具有现实意义[1]。北方工业大学研制的定模动辊成型装备，将具有特定轮廓的轧辊顺序组合，对金属板材进行沿模具型面渐进成型，从而得到变化的横截面形状，是一种节能高效的变截面辊弯成型设备,如图1所示[2]。在金属成型过程中，运动加速度对材料的成型质量以及成型过程有着较大影响，所以减小加速度峰值，增加运动的平稳性是需要研究的装备性能优化问题。文中以加速度为目标函数，开展定模动辊成型机的动力学优化。

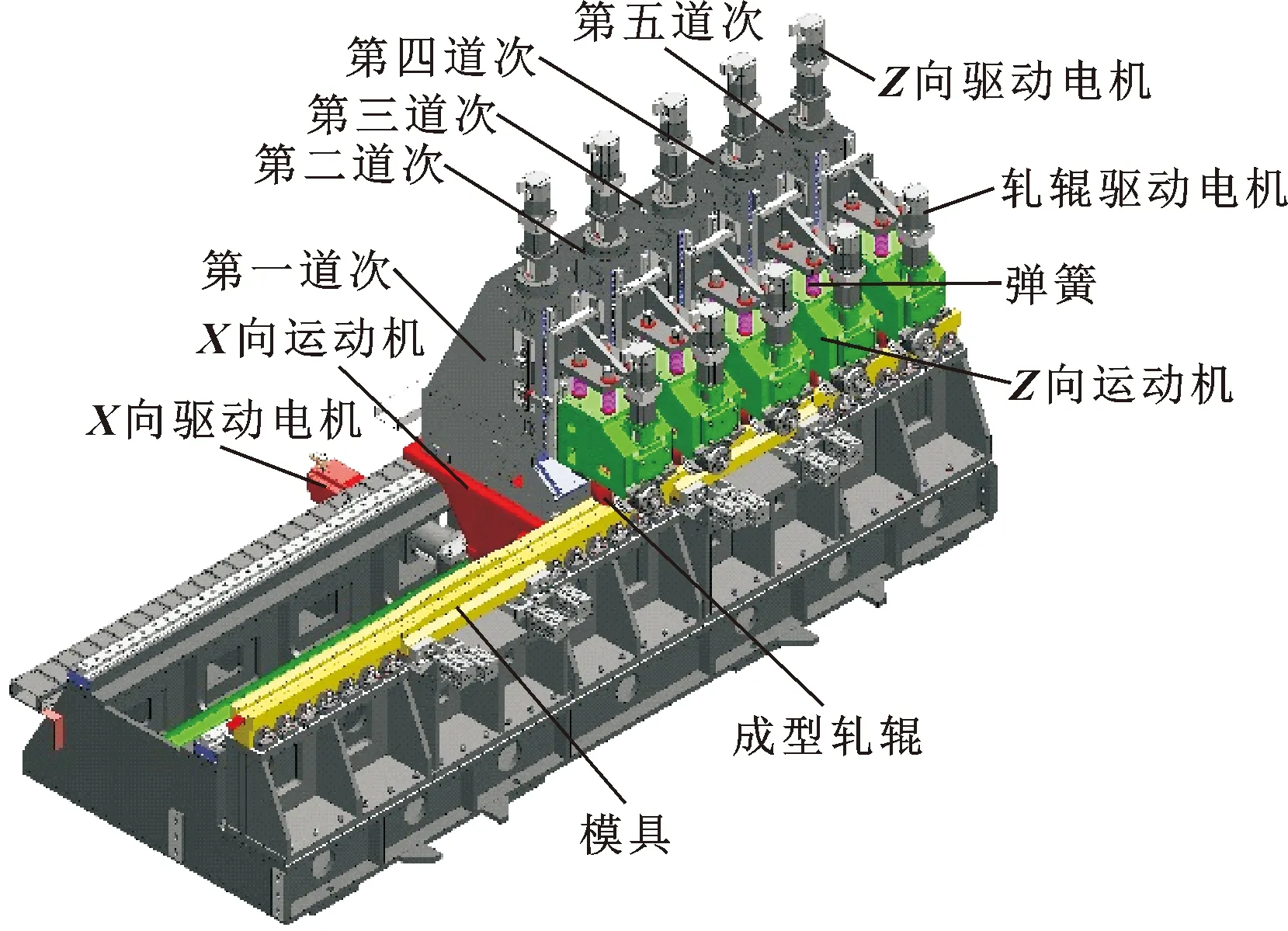
图1 定模动辊成型机三维模型

定模动辊成型装备机电系统动力学优化涉及装备伺服电机、传动装置、辊模机构与成型板材复杂系统，构成复杂，影响因素多，属于高耦合、多极值、多优化变量的优化问题。传统的优化方法如牛顿法等，适合凸函数优化，无法在多极值的优化问题中取得良好效果[3]。粒子群算法是源于对鸟群的研究提出的一种群体智能优化方法，具有并行性、鲁棒性、记忆性等优点而在优化领域有着广泛应用[4]。

近些年来，人工智能的兴起提供了一种新的优化思路。目前比较火热的自动驾驶，机器人自动学习，以及以AlphaZero为代表的棋类智能软件，都应用到深度强化学习[5]。深度强化学习是一种自动学习最优策略的机器学习方法，它采用概率模型或者策略函数输出动作与环境交互，用动作值函数计算该动作的值，通过不断与环境交互找到动作值最大的最优动作[6]。与粒子群迭代寻优方法相比，深度强化学习方法输出的动作之间关联性较小，能够更充分地探索环境，找到更优动作。

深度确定性策略梯度(Deep Deterministic Policy Gradient，DDPG)算法是应用于连续动作空间的深度强化学习算法，在连续动作空间中有着良好表现[7]。LIANG等[8]利用DDPG算法对电力市场进行建模，分析电力市场均衡问题;RODRIGUEZ-RAMOS等[9]将DDPG算法应用到无人机着陆。机电系统动力学优化属于高位连续动作空间问题，本文作者采用DDPG算法对定模动辊弯机电系统进行动力学优化。

1 动力学优化的强化学习模型

1.1 强化学习

强化学习是解决动作与环境交互生成的马尔可夫决策过程(Markov Decision Process，MDP)问题的一类算法，其基本结构如图2所示[6]。

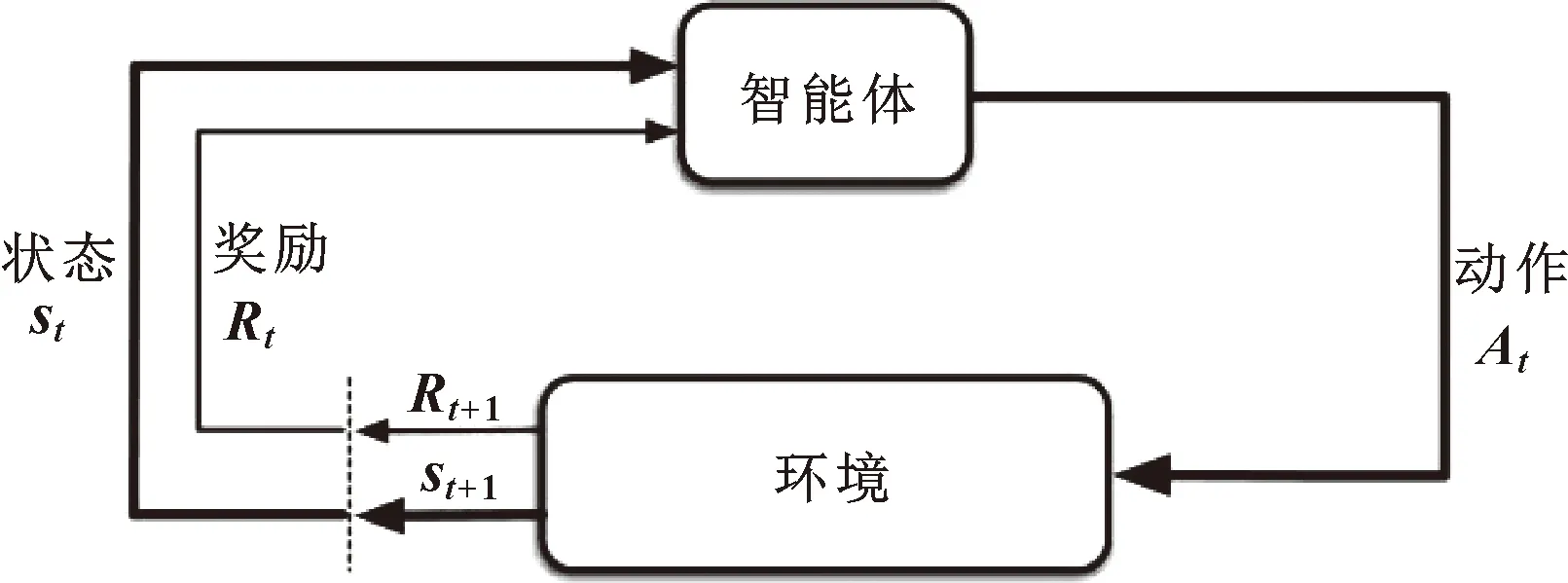
图2 强化学习框架

强化学习首先包括2个基本的交互对象：智能体(Agent)与环境(Environment)。Agent能够感知环境的状态来选择动作，并根据环境反馈的奖励来调整策略实现决策与学习的功能；环境能够接收Agent选择的动作并改变其状态，并反馈给Agent对应的奖励。

Agent与环境交互学习的动态过程就是一个MDP。MDP包括以下几个要素：

(1)状态空间S={s0,s1,…,si}，表示环境所有状态信息的集合。

(2)动作空间A={a0,a1,…,ai}，表示Agent所有动作的集合。

(4)奖励函数R(st,at)用来描述Agent选择动作的奖励，奖励函数的设置与要实现的目标一致。

策略π(s)是Agent根据状态s选择动作a的依据。策略分为确定性策略(Deterministic Policy)与随机性策略(Stochastic Policy)2种。确定性策略是指对于一个状态，策略只会输出一个动作，即每一个状态s都对应唯一的一个确定动作a；随机性策略则是指对于一个环境状态s，Agent可以选择多个动作，每个动作对应一个概率，这些动作的概率相加之和等于1：

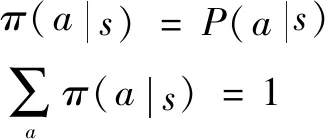
(1)

强化学习的目标是找到一个最优的动作，使得Agent在状态s下得到的累积期望奖励最大；因此强化学习的目标转换为Agent学习到一个最优的策略，使得Agent由该策略得到的动作、累积期望奖励最大。

设Agent基于策略π与环境交互得到的一条轨迹为

τ={s0,a0,r1,s1,a1,r2,…,st-1,at-1,rt,st,…}

则这条轨迹的累积期望奖励定义为

(2)

其中:0<γ<1表示折扣系数。

为了定量描述策略π反馈的累积期望奖励的大小，定义2个价值函数：状态值函数与状态-动作值函数。状态值函数Vπ(s)表示Agent在状态s下采用策略π得到的累积期望奖励。其定义如下：

γVπ(s′)]

(3)

其中:s为当前时刻状态；a为在s下Agent遵循策略π得到的动作；s′为s下一时刻的状态。

式(3)也叫作状态值函数的贝尔曼方程。通过状态值函数的贝尔曼方程，当前状态的值函数可以通过下一时刻状态的值函数计算。

动作-状态值函数Qπ(s,a)也叫Q函数或动作值函数，表示在状态s下，Agent遵循策略π，依据动作概率选择动作a得到的累积期望奖励。Qπ(s,a)的定义如下：

(4)

将公式(3)与公式(4)对比可得：Vπ(s)就是在状态s、Agent遵循策略π下，对所有动作Qπ(s,a)的期望。所以Vπ(s)与Qπ(s,a)二者之间的关系为

(5)

将公式(5)代入公式(4)得到Qπ(s,a)的贝尔曼方程：

(6)

其中：a′为Agent在s′下遵循策略π选择的动作。

1.2 定模动辊成型装备机电系统动力学的强化学习模型

基于能量守恒定律得到五道次定模动辊弯成型机的动力学模型[10]：

j=1,2,…,11

(7)

在成型过程中，五道次定模动辊成型装备X向运动大机架运动的平稳性与材料的最终成型质量直接相关。因而，选择大机架的加速度为优化对象，减小加速度的峰值降低速度的波动程度，提高运动的平稳性。所以，优化目标函数为

(8)

选定定模动辊成型装备机电系统参数作为设计变量[11]，其取值范围如表1所示。

表1 设计变量及其取值范围

定模动辊成型装备机电系统动力学的强化学习模型定义如下：

(1)环境L。将定模动辊成型装备的动力学方程定义为强化学习的环境。

(2)动作空间A。将8个优化变量定义为动作a。

(3)状态空间F。将动作a代入到环境L中，通过龙格-库塔法求解动力学方程得到加速度峰值f=L(a)，加速度峰值f定义为状态。

(4)奖励函数τ。优化目标是降低加速度峰值，因此，加速度峰值减小越多则奖励应该越大。所以，奖励函数定义为：τi=f0-fi,f0表示定模动辊成型装备未优化时状态,fi表示任意一组动作对应的状态。

2 优化算法——深度确定性策略梯度算法

2.1 基于标准MDP的深度确定性策略梯度算法

在强化学习算法族中，深度确定性策略梯度(DDPG)算法是深度神经网络在强化学习算法中的一个成功应用，它在连续高维动作空间问题有着良好表现[7]。DDPG算法是一个基于确定性策略梯度的无模型、演员-评论家算法。演员-评论家算法包含一个策略函数和一个动作值函数：策略函数作为一个演员，生成动作并与环境交互；动作值函数作为一个评论家，对演员的表现进行评价并指导演员的后续动作。

DDPG算法采用2个深度神经网络T(f,a|θT)，μ(fθμ)分别近似动作值函数Tμθ(f,a)、策略函数μθ。其中，θT、θμ分别表示T(f,a|θT)、μ(f|θμ)的参数。

定义T(f,a|θT)损失函数为

(9)

其中：yi=ri+γTμθ[si+1,μθ(si+1)]，γ表示折扣。所以，为了最小化损失函数L(θT)，利用梯度下降法更新T(f,a|θT)的参数θT[12]：

θT←θT-λ∇θTL

其中:λ为学习率。

T(f,a|θT)关于θμ的梯度为

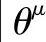
(10)

SILVER等[13]证明公式(10)为确定性策略梯度。μ(f|θμ)的目标是最大化T(f,a|θT)，因此参数θμ按照梯度上升法更新：

θμ←θμ-λ∇θμJ

(11)

2.2 神经网络设置

文中采用前馈全连接神经网络表示μ(f|θμ)与T(f,a|θT)。由第1.2节可得，策略函数的输入为状态f，输出为动作a。因此，策略网络μ(f|θμ)的输入层为1个神经元，输出层为8个神经元。隐藏层采用两层，神经元分别为400、300。所以，μ(f|θμ)第二层的输入为

K2=ω1,2z2

(12)

第二层输出为

P2=g(K2)

(13)

μ(f|θμ)第三层输入为

K3=ω2,3P2+z3

(14)

第三层输出为

P3=g(K3)

(15)

μ(f|θμ)输出层的输入为

K4=ω3,4P3

(16)

输出层的输出为

y=l(K4)

(17)

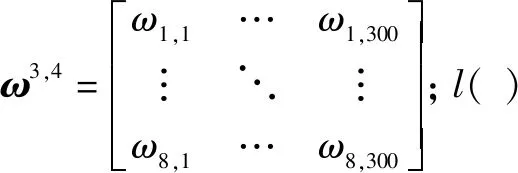
动作值函数计算环境在状态f与动作a下得到的期望累积奖励，因而动作值函数的输入为f与a，输出为动作值Tμθ(f,a)。所以，动作值网络T(f,a|θT)的输入层为9个神经元，输出层为1个神经元，隐藏层同样采用两层，神经元分别是400、300。输出层没有激活函数，直接输出神经网络计算出的动作值。

2.3 激活函数

在上面神经网络各层之间，g( )与l( )分别为神经网络层的激活函数。神经网络中每层神经元的输入可以表示为：H=ωTx+b。激活函数在神经网络中目的是引入非线性因素，提高神经网络的非线性逼近能力。因此每个神经元的输出为u=f(z)，f( )表示激活函数。

T(f,a|θT)与μ(f|θμ)的隐藏层采用ReLU函数作为激活函数，因此：

g(x)=ReLU(x)=max(0,x)

(18)

神经网络在反向梯度传递时，很容易发生梯度消失，相比较于其他激活函数，ReLU函数计算速度快，解决了梯度消失问题，因此采用ReLU函数作为中间层的激活函数。

T(f,a|θT)输出层不采用激活函数，直接输出动作值网络的计算结果；μ(f|θμ)的输出层则采用tanh函数：

(19)

tanh函数将神经元的输出限定在[-1,1]之间，因此策略网络输出的动作值在[-1,1],所以采用区间变换,将动作值从[-1,1]转换到原区间。

设动作a=[a1,…,a8]第i个优化变量ai的原取值范围为[m,n]，因此区间变换公式为

(20)

2.4 神经网络学习样本

(21)

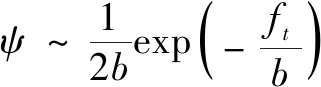
2.5 神经网络学习

MNIH等[15]最先证明，采用经验缓存和目标神经网络冻结可以提高神经网络训练的效率以及鲁棒性。经验缓存指建立一个经验池D将wi={fi,ai,τi,fi+1}作为一组数据存储到D内，D={w1,w2,…,wR}。当D存满数据时，采用随机抓取的方法在D内抓取数据训练神经网络，随后Agent继续与环境交互生成新的数据存入经验池D内覆盖旧数据。

设神经网络每次训练从经验池D抓取N个wi。由T(f,a|θT)的损失函数可得，yi为目标动作值。因此建立目标策略网络μ′(f|θμ)与目标动作值网络T′(f,a|θT′)计算yi。所以，第i个目标动作值:

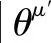
(22)

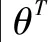
(23)

策略网络的更新为

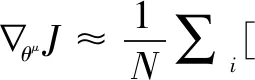
(24)

2.6 目标神经网络参数更新

目标神经网络的作用是计算目标动作值，如果目标动作值与实际动作值采用一个神经网络计算，则当神经网络参数更新时，目标动作值也会发生改变导致神经网络最终无法收敛。因此建立目标神经网络μ′(f|θμ′)与T′(f,a|θT′)，μ′(f|θμ′)与T′(f,a|θT′)参数θμ′、θT′会在一定的时间内保持不变，当主网络更新一定的次数后，目标网络的参数会采用软更新的方法，如公式(25)所示，ξ为软更新系数。

(25)

所以，基于MDP的DDPG算法进行定模动辊机电系统动力学优化的流程为：

第一步：初始化神经网络参数θμ、θT、θμ′=θμ，θT′=θT。

第二步：初始化经验池D大小R。

第三步：For episode=1 toP:

第四步：初始化动作噪声ψ。

第五步：Fort=1 toK:

第六步：μ(s|θμ)基于状态fi输出动作ai，将μ(f)=ai+ψ代入到动力学方程，采用龙格-库塔法求解动力学方程得到状态fi+1，用奖励函数τ(f,a)计算τi。

第七步：将wi储存到经验池D。

第八步：if 经验池=TRUE:

更新Q(s,a|θT)：

θT←θT-λ∇θTL

更新μ(s|θμ)：

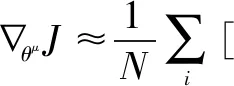
θμ←θμ+λ∇θμJ

更新μ′(s|θμ′)Q′(s,a|θQ′)：

θμ′←ξθμ-(1-ξ)θμ′

θT′←ξθT-(1-ξ)θT′

End if

End for

End for

3 优化结果分析

3.1 算法参数设置

文中采用前馈全连接神经网络。上述优化过程中，神经网络的节点、层数、权重等参数如表2所示,其中N(0,0.1)表示高斯分布。DDPG算法其余参数设置如表3所示。

表2 神经网络参数设置

表3 DDPG算法参数设置

3.2 优化过程分析

基于DDPG算法得到的T(f,a|θT)与μ(f|θμ)的训练过程，以及每轮次总奖励值变化如图3、图4、图5所示。

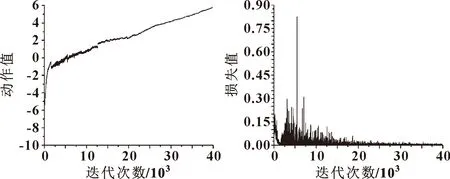
图3 μ(f|θμ)训练过程 图4 T(f,a|θT)训练过程

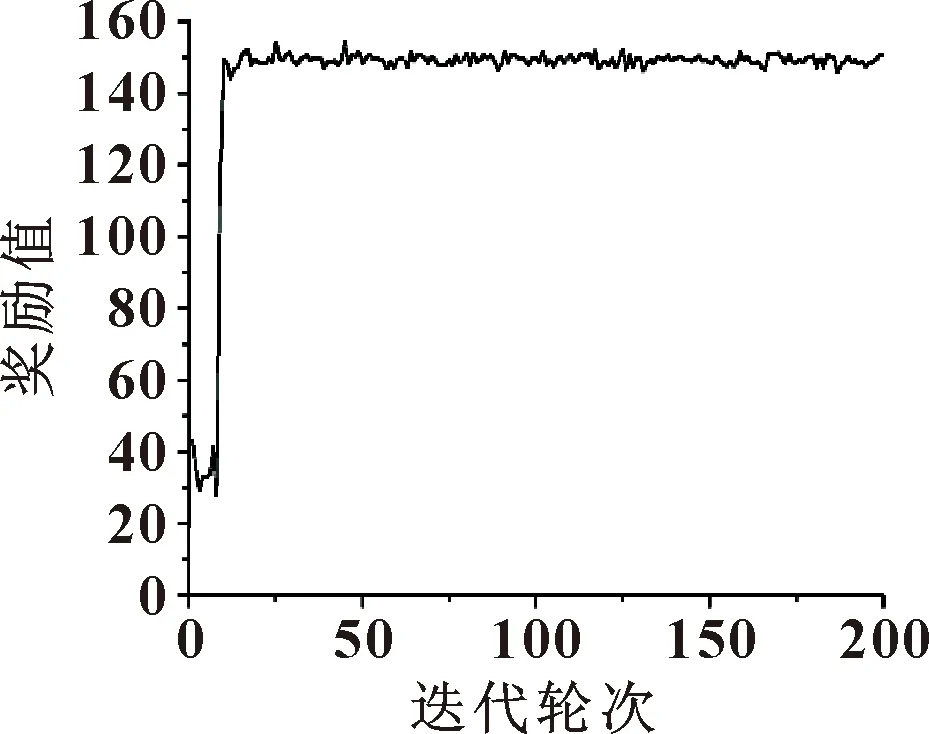
图5 每轮次奖励值

由图3可得:随着Agent不断学习，算法找到的策略的动作值也在不断上升。在0～5 000次，动作值从-10上升到0，在5 000～40 000次动作值从1上升到6左右。图4中动作值网络的损失值在0～5 000次下降得非常迅速，在5 000次后逐渐收敛到0。图5显示的是每轮次的奖励值之和，由图5可得：在0～25轮次中，奖励值的变化幅度最大，在25轮次之后，奖励值基本稳定在150左右，表明算法已经收敛。

3.3 优化结果分析

DDPG算法优化前后的8个变量取值如表4所示。

表4 设计变量优化结果

优化前后得到的加速度图像对比如图6所示。

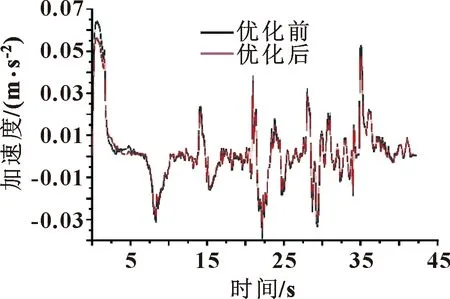
图6 优化结果对比

由图6可得：优化后的加速度曲线整体比优化前减小，在0～2 s内的加速度峰值由0.062 9 m/s2降低到0.055 2 m/s2。这表明基于强化学习方法的动力学优化有着显著的优化效果。

4 结论

文中基于强化学习“试错”学习最优策略的思想，采用DDPG算法对五道次定模动辊弯机电系统进行动力学优化，研究可得：

(1)深度强化学习方法在多参数、多极值、多优化变量的优化问题中有着良好表现，能够应用于机电系统动力学优化工程问题。

(2)通过采用深度强化学习方法优化辊弯成型设备，提高了设备的运行性能，为工业大批量生产提供了理论依据。

(3)以定模动辊弯成型机为对象，验证深度强化学习在机电系统动力学优化的应用效果，建立了机电系统动力学优化的一般马尔科夫决策模型，为机电系统动力学优化提供新的优化思路与方法。