基于LASSO-ISAPSO-ELM的含蜡原油管道蜡沉积速率预测

骆正山，潘柯成

(西安建筑科技大学管理学院,陕西 西安 710055)

管道运输是我国含蜡原油的主要运输方式[1]。因管道内部条件变化而导致的原油蜡分子析出会对管道带来蜡沉积问题[2]。蜡沉积会增大管道运输的阻力，提高生产成本，严重情况下甚至会造成管道堵塞，引发破坏性事故[3]。因此，探究含蜡原油管道中蜡沉积的形成规律，构建有效的蜡沉积速率预测模型，对于含蜡原油管道的安全生产具有重要的现实意义。

目前，国内外诸多学者已采用多种方法对含蜡原油管道蜡沉积速率进行了研究，如Liu等[4]、王凤辉等[5]、叶兵等[6]和张在孝等[7]分别采用热力学模型、Fick 扩散模型、OLGA软件仿真和室内环道试验的方式，针对不同的含蜡原油管段对其蜡沉积速率进行了有效预测。虽然研究成果尚佳，但上述研究均需进行大量的油品试验，研究成本较高且普适性差，难以应用于工程实践。此外，也有部分学者将机器学习技术引入到含蜡原油管道蜡沉积速率预测中，如田震等[8]、Xie等[9]、王磊等[10]和靳文博等[11]分别证实了反向传播(Back Propagation，BP)神经网络、径向基函数(Radial Basis Function，RBF)神经网络、支持向量机(Support Vector Machines，SVM)和最小二乘支持向量机(Least Square Support Vector Machine，LSSVM)用于含蜡原油管道蜡沉积速率预测的可靠性。但这些研究缺少对含蜡原油管道蜡沉积速率影响因素的客观筛选，且在预测模型方面，BP神经网络和RBF神经网络需要大量样本作为数据支撑，存在运行速度慢、预测效率差的缺陷；SVM和LSSVM的核函数参数确定困难，采用的传统优化算法收敛速度慢、易陷入局部最优，影响了模型的实用价值。

鉴于此，本文提出一种将套索算法(LASSO)、改进的模拟退火粒子群优化算法(ISAPSO)和极限学习机(ELM)有机结合的含蜡原油管道蜡沉积速率预测新方法，该方法首先采用LASSO选取影响蜡沉积速率的重要因素，简化样本集；然后用ISAPSO对ELM的参数进行优化，建立基于LASSO-ISAPSO-ELM的含蜡原油管道蜡沉积速率预测模型；最后以青海某厂原油室内环道试验数据为例进行实例研究，对模型性能进行了验证和分析。

1 基础理论

1.1 套索算法(LASSO)

含蜡原油管道蜡沉积速率受多种因素的影响，预测时若将影响较小的因素作为输入项代入模型，不仅会增加模型的训练时间，还会对模型训练的拟合度产生负面干扰，从而降低模型的预测精度，因此在预测前应对影响因素进行筛选，选出关键影响因素。套索算法(Least Absolute Shrinkage and Selection Operator，LASSO)是一种自变量选择方法，该方法通过引入一个惩罚函数的方式将影响较小的自变量系数压缩为0，从而将这些自变量剔除[12]。在此可利用LASSO达到因素筛选的目的。

假设初始数据集为(Xn,Yn),n=1,2,…,N，其中Xn=(xn1,xn2,…,xnm)T为自变量矩阵，Yn为因变量矩阵。令系数矩阵β=(β1,β2,…,βm)T，假定经归一化处理的Xn无一般损失，则LASSO的估计量可以表示为

(1)

其中，λ为惩罚因子，该参数越小，则惩罚度越小，模型中存留的自变量越多；反之，存留的自变量越少。可采用K折交叉验证法确定λ的最优参数。

1.2 模拟退火粒子群优化算法(SAPSO)

模拟退火粒子群优化算法(Simulated Annealing Particle Swarm Optimization，SAPSO)是基于粒子群优化算法(Particle Swarm Optimization，PSO)延伸出的一种具备跳出局部最优能力的元启发式优化算法[13]。SAPSO算法迭代时，计算每个粒子的适应度增量ΔE，依据Metropolis准则，若ΔE<0，即新解较优，则接受较优解；若ΔE>0，即新解较差，则以概率p接受较差解。该算法中速度v、位置z和概率p的具体表达如下：

vi,d(k+1)=wvi,d(k)+c1r1[pi,d(k)-zi,d(k)]+c2r2[pg,d(k)-zi,d(k)]

(2)

zi,d(k+1)=zi,d(k)+vi,d(k+1)

(3)

p=exp(-ΔE/T)

(4)

式中:i为粒子序号,i=1,2,…,I；d为维度,d=1,2,…,D；k为当前迭代次数,k=1,2,…,K；ω、c1和c2分别为惯性权重和两个学习因子，一般赋予固定值；r1和r2为0到1之间的随机数；pi,d和pg,d分别为个体最优位置和群体最优位置；T为退火温度，寻优前期，较高的退火温度可确保粒子迭代的随机性，避免算法陷入局部最优，而寻优后期，退火温度逐步下降，粒子迭代趋于稳定，算法向最优解收敛。

1.3 极限学习机(ELM)

极限学习机(Extreme Learning Machine,ELM)是基于单隐层的新型前馈神经网络，因其具有泛化能力强、人为操作少、训练速度快的优势，在预测领域中已被广泛应用[14]。假定经第1节自变量筛选后的简化数据集为(An,Yn)，其中An=[an1,an2,…,anf]T∈Rn，Yn=[y1,y2,…,yn]T。则拥有L个隐含层节点的单隐层神经网络可用如下公式表示：

(5)

式中:g(x)为激活函数；Wl=[wl1,wl2,…,wlf]T和el分别为输入权重和第l个隐含层节点阈值，由系统随机生成；θl为输出权重。

将公式(5)用矩阵表达如下：

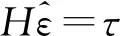
(6)

2 模拟退火粒子群优化算法(SAPSO)的改进

2.1 种群初始化的改进

SAPSO采用的随机初始化策略无法保证粒子初始位置的遍历性，致使部分粒子远离最优解，从而降低了算法的求解速度[15]。对此，可引入Tent混沌策略对算法初始化进行改进，但标准的Tent混沌策略存在小周期问题，且当混沌值为0、0.25、0.5和0.75时序列失效，需重新赋值[16]。因此，引入随机干扰项对Tent混沌策略进行改进，并利用改进的Tent混沌策略对粒子进行初始化，其表达如下：

(7)

式中:rand(1,0)为[0,1]内的随机数。

2.2 惯性权重和学习因子的改进

惯性权重(ω)和学习因子(c1、c2)控制粒子的寻优趋向和收敛速度。惯性权重较大且当学习因子c1>c2时，粒子趋向于全局寻优且收敛速度较快；反之，则粒子趋向于局部寻优且寻优精度较高。SAPSO的特点要求粒子在寻优前期趋向于全局寻优且具备较快的收敛速度；寻优后期趋向于局部寻优且具备较高的收敛精度[17]。

鉴于采用定值赋值策略无法满足上述要求，因此基于双曲正切函数构建惯性权重和学习因子随迭代次数增加而动态匹配的策略，具体表达如下：

ω(k+1)=[ωa+tanh(-8+16(K-k)/K)·ωs]/2

(8)

c1(k+1)=[ca+tanh(-8+16(K-k)/K)·cs]/2

(9)

c2(k+1)=[ca-tanh(-8+16(K-k)/K)·cs]/2

(10)

式中:(·)a为该参数的最大值与最小值之和；(·)s为该参数的最大值与最小值之差。

2.3 算法改进前后的对比

设粒子数量和最大迭代次数为200次，改进前的ω、c1和c2分别取固定值0.65、2.25和1.75；改进后的ω最大值和最小值分别取0.9和0.2，c1和c2的最大值和最小值分别取2.75和1.25。改进前后粒子初始化结果分别如图1和图2所示，惯性权重和学习因子的变化趋势如图3和图4所示。

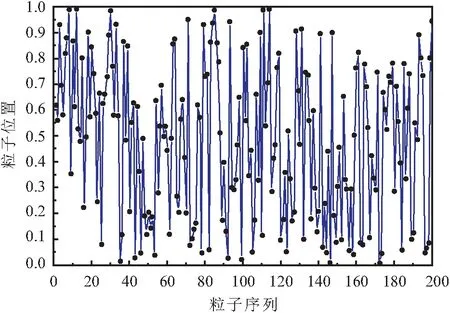
图1 随机初始化粒子

对比图1和图2可知，采用改进Tent混沌的初始化策略，有效地增强了粒子遍历性，避免了粒子区域的大面积空白。

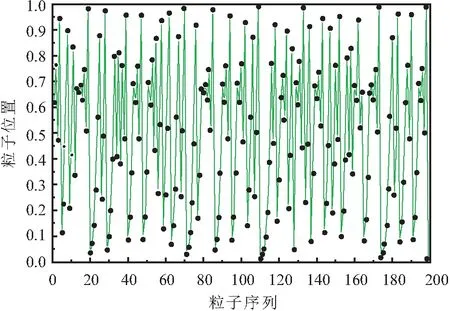
图2 改进Tent混沌策略的初始化粒子

由图3和图4可知：惯性权重和学习因子动态匹配的策略使算法的参数与算法特点相适应， 寻优前期惯性权重处于最大值，下降速度缓慢，且学习因子差值更大，故全局搜索能力更强，收敛速度更快，更易于跳出局部最优；寻优后期惯型权重快速递减，两个学习因子的变化与之匹配，故局部搜索能力更优，寻优精度更高。

图3 惯性权重的变化趋势

图4 学习因子的变化趋势

3 基于LASSO-ISAPSO-ELM的含蜡原油管道蜡沉积速率预测模型构建

3.1 模型构建

基于LASSO-ISAPSO-ELM的含蜡原油管道蜡沉积速率预测模型构建流程如图5所示。具体描述如下：

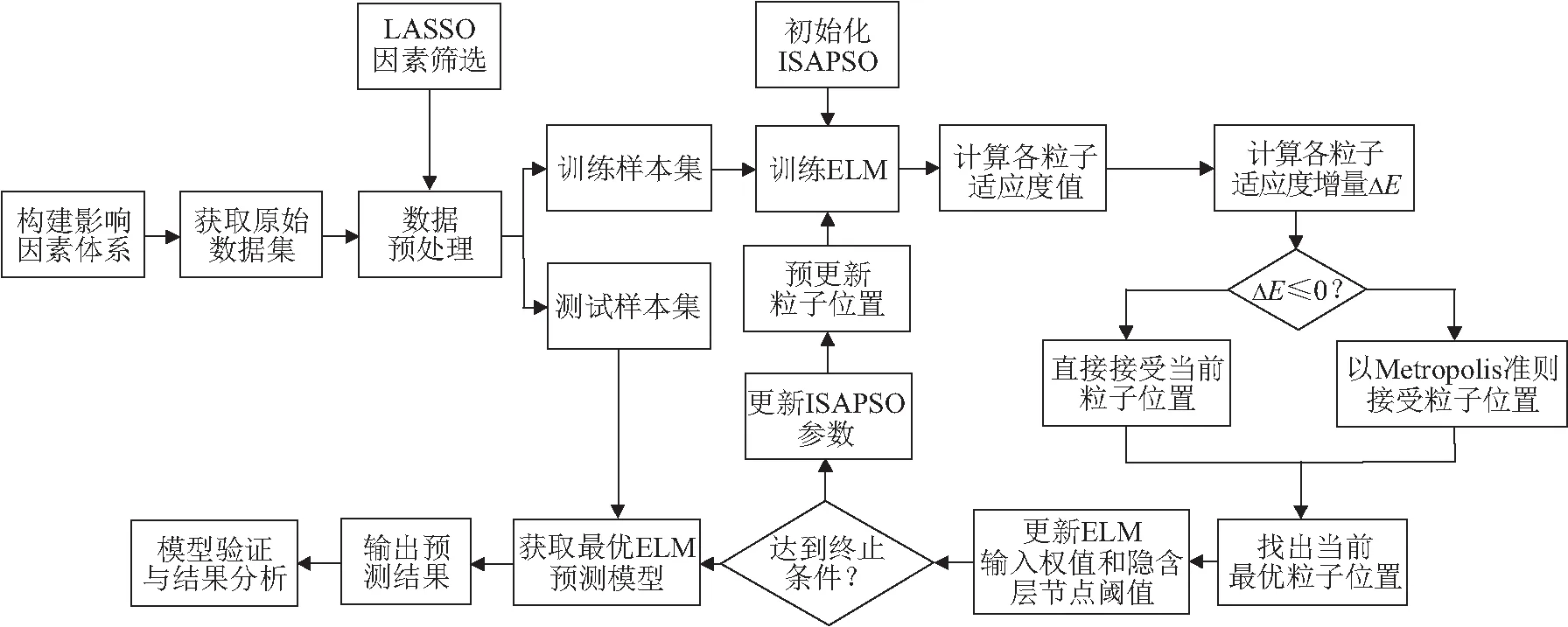
图5 基于LASSO-ISAPSO-ELM的含蜡原油管道蜡沉积速率预测模型流程

(1) 构建含蜡原油管道蜡沉积速率影响因素体系。根据具体工况，收集并整理含蜡原油管道蜡沉积速率数据集，并采用如下公式对数据进行预处理：

(11)

式中:xnm第n条数据的第m种影响因素数值，xmmax和xmmin分别为第m种影响因素的最大值和最小值。

(2) 采用10折交叉验证法确定LASSO的惩罚因子，对数据集中的影响因素进行筛选。

(3) 将简化后的数据集以4∶1的比例随机划分为训练集和测试集，代入训练集训练ELM的过程中引入ISAPSO对其进行优化。采用均方根误差(Root Mean Square Error，RMSE)作为适应度函数，通过ISAPSO不断迭代，以公式(3)和(4)更新粒子位置，寻找ELM最优的Wl和el组合，使得RMSE值最小，得到最优的含蜡原油管道蜡沉积速率预测模型。

(4) 输入测试集样本到最优预测模型中，得到含蜡原油管道蜡沉积速率的预测值，并与其他模型的预测结果进行对比分析。

3.2 模型评价

为了验证模型的预测效果，采用均方根误差(RMSE)、平均相对误差(Mean Relative Error，MRE)和希尔不等系数(Theil IC)对模型优劣进行评价，具体计算公式如下：

(12)

(13)

(14)

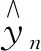
希尔不等系数介于0～1之间，其值越趋于0,表明模型预测误差越小，模型预测性能更佳。

4 实例应用与分析

4.1 影响因素体系构建与数据获取

通过对相关文献[9,18-19]的总结梳理及软件仿真，构建含蜡原油管道蜡沉积速率的影响因素体系，其中包含油温(F1)、壁温(F2)、黏度(F3)、管壁剪切应力(F4)、流速(F5)、管壁处温度梯度(F6)和管壁处蜡分子浓度梯度(F7)7个影响因素。

本研究以青海某厂原油为试验油样进行室内环道试验，其试验装置如图6所示。具体试验步骤如下：

图6 小型室内环道试验装置

(1) 将搅拌罐内原油升温至指定温度并恒温静置15 min，再调节参照管和测试管温度，使其与油温相同，以防油流进入后提前发生蜡沉积现象。

(2) 管道开泵，将罐内原油抽入环道内运转15 min，使油流充分冲刷管道，以排出管内空气。

(3) 数据采集前，将采集设备的数值归零，之后调节流量，待流量值稳定后将测试管壁温迅速调节至油温以下的指定温度，开始采集时间、压差、流量、流速等试验数据，并通过压差法即可计算得到测试管内的蜡沉积速率。

(4) 每轮试验完毕，将管道壁温升高并调大流量，对管道内部的蜡质进行冲刷，当参照管与测试管段各自压差大致相等时停泵，接入吹扫系统，将管道内蜡沉积物和余油吹扫至罐内，完成油样的回收再利用。

通过室内环道试验，获取该青海某厂原油蜡沉积速率数据集85组，部分原始数据如表1所示。

表1 室内环道试验各影响因素和蜡沉积速率的原始数据

4.2 LASSO的影响因素筛选

采用10折交叉验证法确定LASSO的惩罚因子λ，10折交叉验证过程如图7所示。

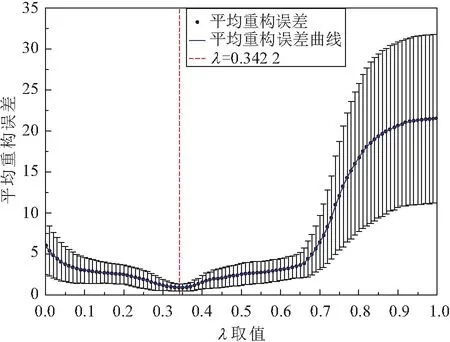
图7 10折交叉验证过程

由图7可知，当惩罚因子λ取值为0.342 2时,其平均重构误差值最低。

图8为LASSO拟合系数轨迹， 其给出了在不同λ取值下各影响因素拟合系数值的变化情况及影响因素的筛选结果。

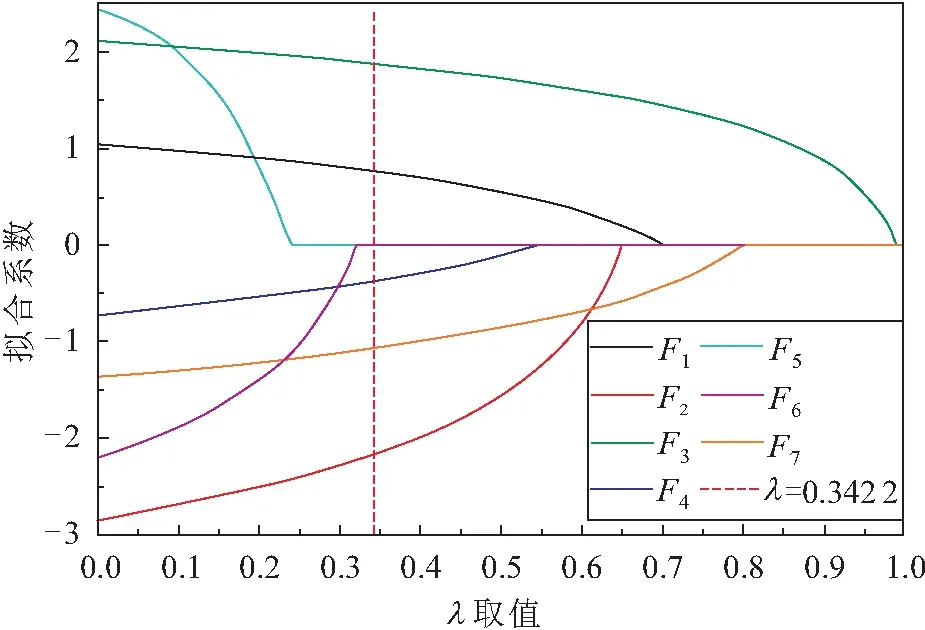
图8 LASSO拟合系数轨迹

由图8可见，当λ值为0.342 2时，F5和F6两项影响因素的系数值收敛为0。

为了分析LASSO筛选含蜡原油管道蜡沉积速率影响因素的可行性，本文对各影响因素进行了灰色关联分析。设分辨系数为0.5，各影响因素与蜡沉积速率的关联度，见表2。

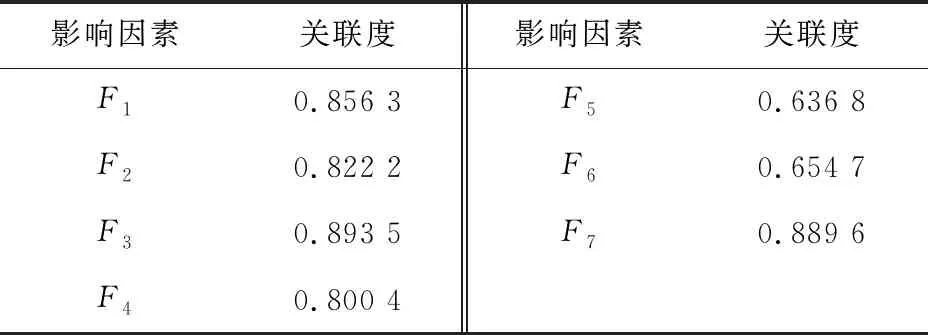
表2 各影响因素与蜡沉积速率的关联度

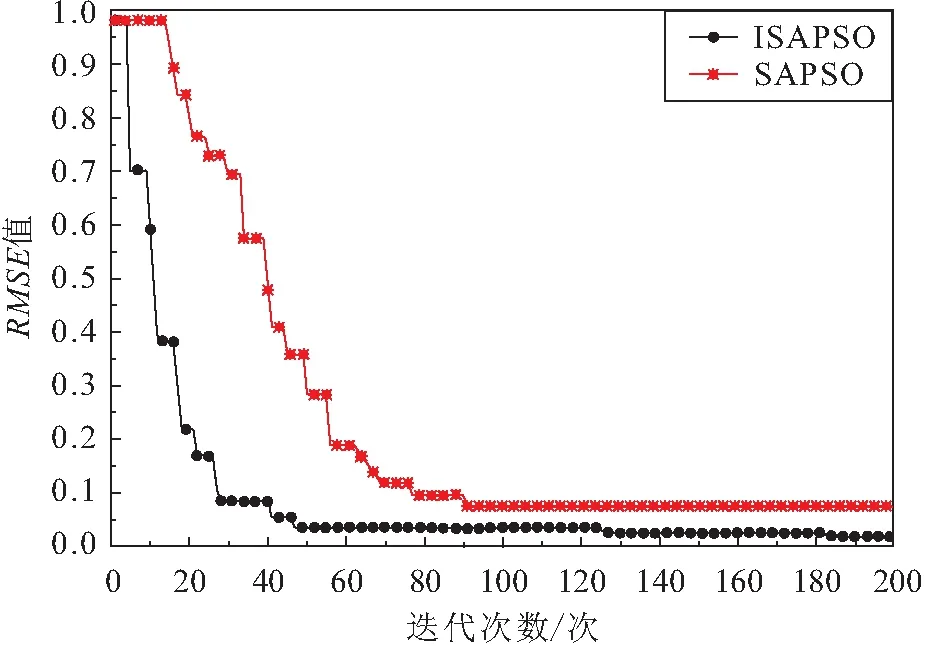
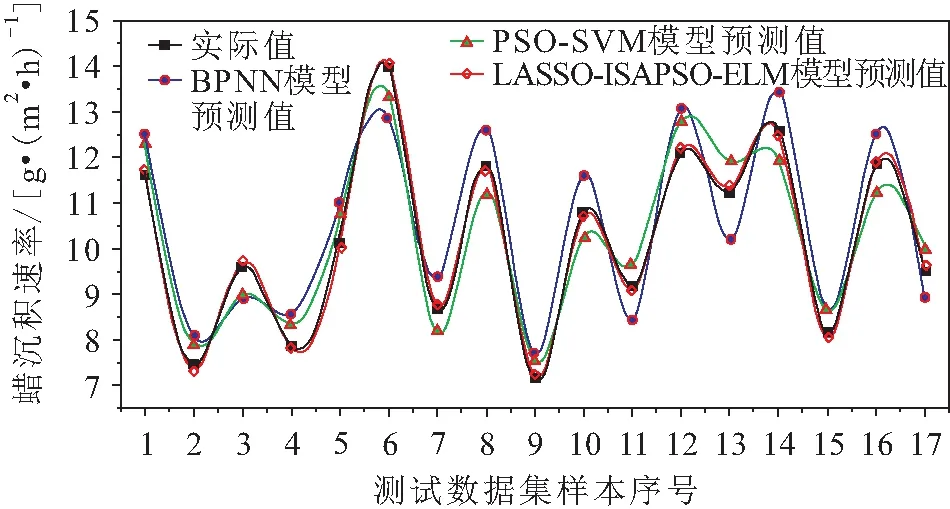
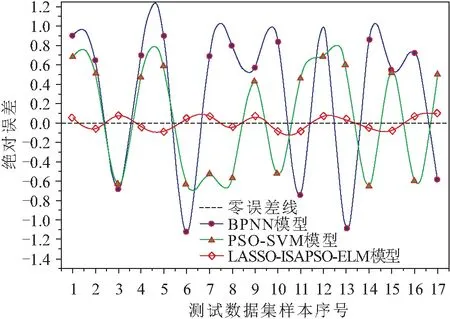
由表2可知，各影响因素与蜡沉积速率的关联度由小到大的排序为：F5

4.3 结果分析与模型评价

设ELM隐含层节点数为30，神经元传递函数为sigmoid函数。为了进一步检验影响因素筛选对模型训练的影响，分别以7项、6项、5项、4项影响因素作为输入项，将随机划分的68组训练集数据代入模型进行训练，通过计算可决系数R2来判定模型训练的拟合度(R2介于0～1之间，R2越趋近于1，表明模型训练的拟合度越高)，并记录模型训练时间。不同输入因素条件下模型训练的可决系数R2和训练时间，见表3。

表3 不同输入因素条件下模型训练的可决系数和训练时间

由表3可知:输入因素项为F1、F2、F3、F4、F7的情况下，R2值最趋近于1，说明模型训练未受到影响较小因素中过多的冗余信息干扰，模型训练拟合度最佳；当输入因素数量为4个时，R2值大幅下降，说明模型由于缺乏关键因素的信息，模型训练处于欠拟合状态，进一步说明LASSO因素筛选的准确性；此外，由于数据量的减少，5项输入因素较7项输入因素相比，其模型训练速度提升近3倍，有效降低了模型训练的时间成本。

为了展现ISAPSO的优势，将其与SAPSO进行对比，算法所有参数与第2.3节相同。在最优输入条件下，模型训练时两种算法的迭代过程对比如图9所示。

图9 模型训练时两种算法的迭代过程对比

由图9可知：寻优前期，较之于标准SAPSO，ISAPSO提前43代趋于收敛，且RMSE值更小，故说明ISAPSO跳出局部最优的能力更强，收敛速度更快；寻优后期，ISAPSO进行局部高精度搜索，最终RMSE值为0.01898，故说明ISAPSO的寻优精度更佳。

为了客观分析本文建立的基于LASSO-ISAPSO-ELM的含蜡原油管道蜡沉积速率预测模型的预测精度，将该模型与BPNN模型[8]和PSO-SVM模型[10]的预测结果进行了对比，其结果见图10、图11、图12和表4。

图10 3种模型预测结果的对比

图11 3种模型预测结果的绝对误差对比

图12 3种模型预测结果的相对误差对比

表4 3种预测模型评价结果对比

由图10至图12和表4可知：LASSO-ISAPSO-ELM模型与BPNN模型和PSO-SVM模型相比，其预测值与实际值更为贴近，未出现差异过大的预测值(见图10)；LASSO-ISAPSO-ELM模型预测结果的绝对误差在±0.1范围内波动，整体趋势更接近0误差线，说明其预测性能更加稳定(见图11)；LASSO-ISAPSO-ELM模型预测结果的相对误差在2%以内，较之于其他模型更小，即LASSO-ISAPSO-ELM模型的预测精度更高(见图12)；LASSO-ISAPSO-ELM模型预测结果的RSME值和MRE值分别为0.069 83和0.693 73%，比其他模型更低，LASSO-ISAPSO-ELM模型预测结果的TheilIC值为0.008 96，较其他模型降低了一个数量级，进一步体现了LASSO-ISAPSO-ELM模型的高预测精度(见表4)。

为了进一步验证LASSO-ISAPSO-ELM模型预测性能的优越性，将上述3种模型重置，均采用相关文献[9,11]中共计63组新数据集对所有模型重新进行训练和测试。其中，训练集和预测集按照50组和13组进行随机划分；LASSO-ISAPSO-ELM模型设置与本文相同，BPNN模型和PSO-SVM模型设置与其对应的文献相同。相关文献[9,11]数据集下3种预测模型评价结果的对比，见表5。

表5 相关文献[9,11]数据集下3种预测模型评价结果的对比

由表5可知，在新的样本数据下，LASSO-ISAPSO- ELM模型预测结果的RMSE值和MRE值依然最低，且TheilIC值依然维持在千分位数量级，表明该模型的预测精度依然最高，进一步说明了该模型对于数据的适应性较强，在含蜡原油管道蜡沉积速率预测中具有明显的优势。

5 结 论

针对含蜡原油管道蜡沉积速率预测问题，本文提出了一种基于LASSO-ISAPSO-ELM组合模型的蜡沉积速率预测新方法。首先，对LASSO、SAPSO和ELM的基础理论进行介绍，并对SAPSO的种群初始化、惯性权重和学习因子3个方面进行了改进；然后，阐述了模型构建的流程，并采用室内环道试验数据对模型进行了训练和预测验证，得到以下结论：

(1) 经LASSO算法筛选的油温、壁温、黏度、管壁剪切应力和管壁处蜡分子浓度梯度5项影响因素可以有效地提升模型训练的拟合度，并降低模型训练的时间成本。

(2) 采用改进的Tent混沌初始化策略并利用双曲正切函数动态匹配调整惯性权重和学习因子，可有效增强SAPSO的寻优能力，使算法的收敛速度加快近一倍，寻优精度亦有所提高。

(3) LASSO-ISAPSO-ELM模型的预测结果与实际蜡沉积速率基本吻合，与BPNN模型和PSO-SVM模型相比，该模型预测精度具有明显的优势，可有效满足实际工况中对含蜡原油管道蜡沉积速率的预测需求，为含蜡原油管道的清管周期制定和安全管理提供了新的决策依据方法。