新型梯形量水堰水力特性试验及数值模拟

高飞飞，李晓庆，2*，高强

(1. 新疆农业大学水利与土木工程学院，新疆 乌鲁木齐 830052； 2. 新疆水利工程安全与水灾害防治重点实验室，新疆 乌鲁木齐 830052)

根据最新水资源公报显示，中国农业用水量占总用水量62.1%以上[1]，在目前水资源短缺的大背景下对农业用水实行节水灌溉势在必行，灌区量水是农业节水灌溉和科学管理水资源的基础和前提[2]，这就要求灌溉渠道尤其是斗、农等末级渠道上安设适应性强、精度高的量水设施[3].梯形量水堰因测量方法简便、结构简单、测流精度高等优点，已成为应用最为广泛的灌区量水设施之一[4].目前对梯形量水堰的研究主要是提高其测流精度，但其测流范围小[5]，泥沙不易通过堰板[6]等问题较少引起关注.当灌溉渠道过流量大于梯形量水堰测流范围时，文献[7-8]提出在量水堰板底部增设孔口，其研究使堰孔组合式量水堰测流范围提高，但其研究仅初步探讨了不同形状底孔对应下的流量公式.为更好地提升堰孔组合量水设施在灌溉渠道上的适用性，文中在改进型堰的基础上提出堰孔组合的新型梯形量水堰，采用室内水工模型试验与数值模拟相结合的方法对不同底孔高度的新型堰进行水力特性试验，并对试验和模拟结果进行分析，找到标准梯形量水堰最合适的孔口高度以及精度较高的测流公式，可为堰孔组合量水设施的推广和应用提供参考价值.

1 新型梯形量水堰结构

《水工建筑物与堰槽测流规范》(SL 537—2011)[9]推荐的堰口边坡坡度特定为4∶1(垂直距离∶水平距离)的6种标准梯形堰系列中，其中最小尺寸为b=250 mm(堰顶宽)，测流范围l测为0.002～0.012 m3/s的标准梯形量水堰，其结构示意图见图1a，结构尺寸参数如表1所示，其余参数含义见文献[9].文中简称为标准型.针对标准型堰测流范围与灌区过流能力不匹配，文献[5]在标准堰的基础上对其进行改进，提出改进型梯形堰(以下简称改进型)，改进型示意图见图1b，主要结构尺寸参数如表1所示.根据实验室场地、供水等条件，并和以往研究学者的成果在同一水平进行对比，文中亦选用堰顶宽为250 mm，并在改进型堰的基础上于渠底同高处增设防淤孔口(以下简称为新型堰)，其孔口宽b均为250 mm，孔高z设置4种规格，分别为30，40，50，60 mm，新型堰主要结构尺寸参数见表1，其结构示意图见图1c.

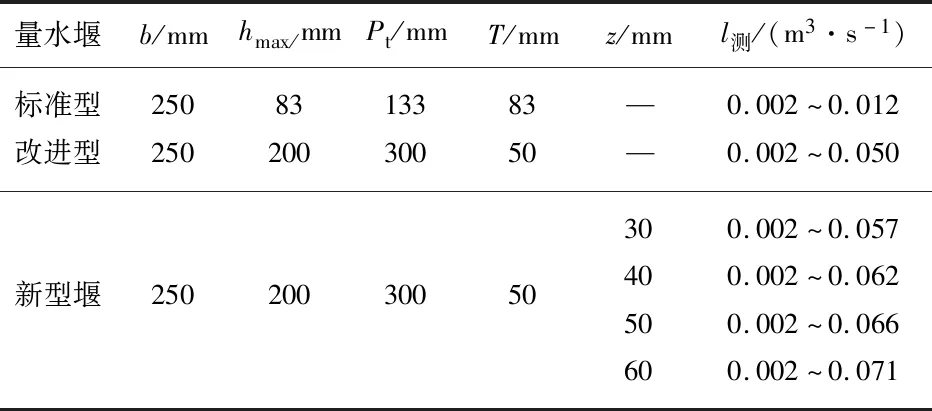
表1 量水堰尺寸参数Tab.1 Dimension parameters of measuring weir

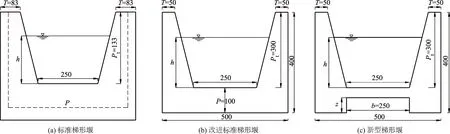
图1 梯形量水堰结构尺寸Fig.1 Structure dimension of trapezoidal measuring weir

2 测流公式理论分析及试验装置

2.1 测流公式理论分析

新型梯形量水堰作为灌区渠道上的一种量水设施，其任务主要是精确地确定过流量，当堰前总水头H>d+z时，过流量由堰流和孔流2个部分组成，形成了典型的堰孔组合式过流，如图2所示.

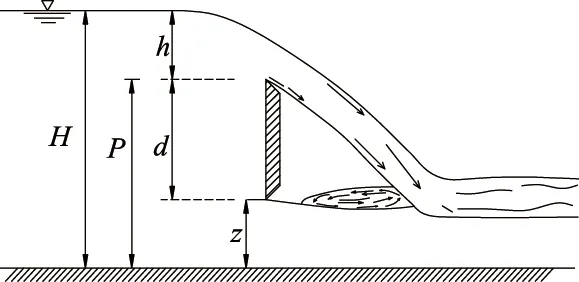
图2 新型堰过流示意图Fig.2 Schematic diagram of new weir overflow

对堰孔同时存在的条件下泄流，SAMANI等[10]分别对孔流和堰流的泄流量进行计算，最后通过叠加给出总泄流量，这种计算流量的方法忽略了孔流与堰流之间的内部作用.文中将修正后的堰上流量和孔口流量相加得到式(1)，即

Q=λQw+ωQo,

(1)

式中:Q为总流量;Qw为通过堰的流量;Qo为通过孔口的流量;λ,ω均为修正系数，将堰流公式、孔流公式[11]代入式(1)可得式(2),即

(2)

式中：b为改进堰堰顶宽度，孔口宽在试验中与堰顶宽度一致，m；z为孔口高度，m；h为堰前水头，m；H为在堰板上游0.8 m处测得的总水头，m；g为重力加速度，m/s2.对式(2)进行改写可得式(3)，即

(3)

由于公式中堰流和孔流的流量系数m,μ不易通过解析法获得，且鉴于试验条件修正系数λ,ω也无法准确得出，对式(3)进行量纲一化分析可得到函数关系式，即

(4)

故新型梯形量水堰测流公式为

(5)

式中:m为综合流量系数；Re为雷诺数，其值为流体惯性力与黏性力之比，是表征流体流动状态的量纲一数，试验中雷诺数Re的值为17 539～50 740，水流状态为紊流，故对雷诺数不予讨论；We为韦伯数，当渠道中新型梯形堰堰前水头h>30 mm时[12]，表面张力对流量的影响较小，因此韦伯数可忽略不计；Fr为佛劳德数；H/z为堰前总水头与孔口高度的比值；h/z为堰前水头与孔口高度的比值.对试验数据进行分析，将建立的定量关系代入式(5)即可得到新型梯形量水堰测的测流公式.

2.2 试验装置

试验系统由供水首部、矩形水槽、回水渠道3个部分组成，如图3所示，首部和回水渠道用来保证矩形水槽中的水流为恒定流.试验系统中水槽尺寸为一长4.5 m、宽0.5 m、高0.5 m的矩形水槽，新型堰堰板采用有机玻璃板制作，共4组堰板；水槽中流量通过首部中阀门进行控制，并用已率定参数的90°三角形堰测量；堰前水头使用SCM60型水位测针测量，精度为±0.1 mm，监测位置取距堰板上游0.8 m处；根据灌区斗、农渠实际流量，试验流量设置了7个水平，调节范围为16～43 L/s，测得了自由出流情况下共35组数据.在测量流量和水头时，需在其稳定的情况下测量，以保证精度，为后续数值模拟模型参数的选择提供参考.

图3 试验系统立面布置示意图Fig.3 Schematic top view of experimental system

3 新型梯形量水堰数值模拟

3.1 湍流模型选择

由2.1可知渠道中水流的流动状态为紊流，故需选择合适的湍流模型对其进行模拟[13].当水流流经堰板时，会因过水断面减小以及堰板的阻挡作用，水面会发生剧烈的变化，RNGk-ε模型比标准k-ε模型在处理高应变率及流线弯曲程度较大的流动有更好的表现，因此选择RNGk-ε模型进行模拟研究，其控制方程中连续方程为

(6)

雷诺方程为

(7)

(8)

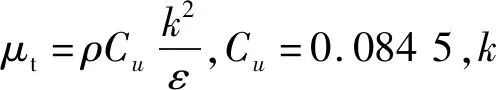
湍动能k方程为

(9)

湍动能耗散率ε方程为

(10)

上述式中：Gk为平均速度梯度引起的湍流动能的产生；C1ε，C2ε为经验值，分别为1.42，1.68.通过给定的实际工况及具体的边界条件，即可得到所求流场各水力参数的分布规律.

3.2 模拟自由水面的VOF法

VOF模型是一种体积流体模型，基本原理为通过引进网格体积比函数Fw实现对每一计算单元相界面的追踪，若某一计算单元Fw(xi，t)=1，即表明该计算单元充满了第i相流体，若某一计算单元Fw(xi，t)=0，说明该单元不存在第i相流体，若Fw(xi，t)∈(0，1)，则表示计算单元包含了第i相流体和其他流体.描述Fw的控制方程为

(11)

将式(11)与湍流数学模型的控制方程式(6)—(10)联立求解，就可获得相应的未知变量，如流速、压力、流线、水体积分数等[14].

3.3 网格划分及边界条件

新型梯形量水堰三维几何模型选用DesignMo-deler软件进行建立，如图4所示，以长4.5 m，宽0.5 m，高0.5 m的矩形水槽为研究对象，选取模型中新型堰堰板右侧底角为原点，x轴正方向为水流方向，z轴负方向为重力加速度方向，y轴正方向为矩形渠道左岸方向.

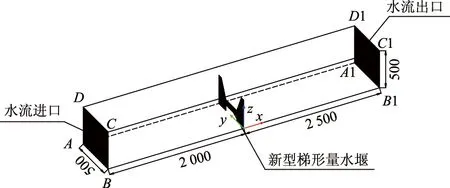
图4 模型计算区域Fig.4 Computational domain of model

在对矩形水槽进行网格划分时，网格画的越密，精度越高，对所得结果的影响越小，但计算时间也随之增加.由于水流流经堰板时，水流变化剧烈，故对堰板附近的网格进行了局部加密处理，经计算局部加密的网格为10 mm时，对所得结果的影响较小，此时计算区域网格数量约24万个.

边界条件设定为水流进口分割成上部空气进口、下部水流进口，并设置上部空气进口为压力入口，下部水流进口为速度入口，并给定进口速度；水流出口为压力出口，模型顶面与大气相通，相对压强定义为0，其余壁面设置为无滑移固壁条件(wall).

利用数值模拟对改进堰及4种孔口高度为30，40，50，60 mm的新型梯形量水堰各进行了总流量Q=16.72，19.32，22.52，27.20，31.37，37.75，42.20 L/s的模拟研究，并以进出口流量差值小于1%作为收敛条件，同时设置了监测断面来监测堰上的出流流量.

4 结果与分析

4.1 堰前水深与流量

根据《灌溉渠道系统量水规范》(GB/T 21303—2017)要求，试验和数值模拟均取距堰板上游0.8 m处的堰前水头进行测量，在Fluent中以水相的体积分数为0.5作为水气交界面，即堰前水头.通过对实测堰前水头和模拟堰前水头值进行对比分析，如表2所示.由表2可知，模拟值与试验值最大相对误差为5.85%，平均相对误差δ为2.53%，说明利用Fluent软件对新型梯形量水堰进行模拟是一种有效可靠的方法.

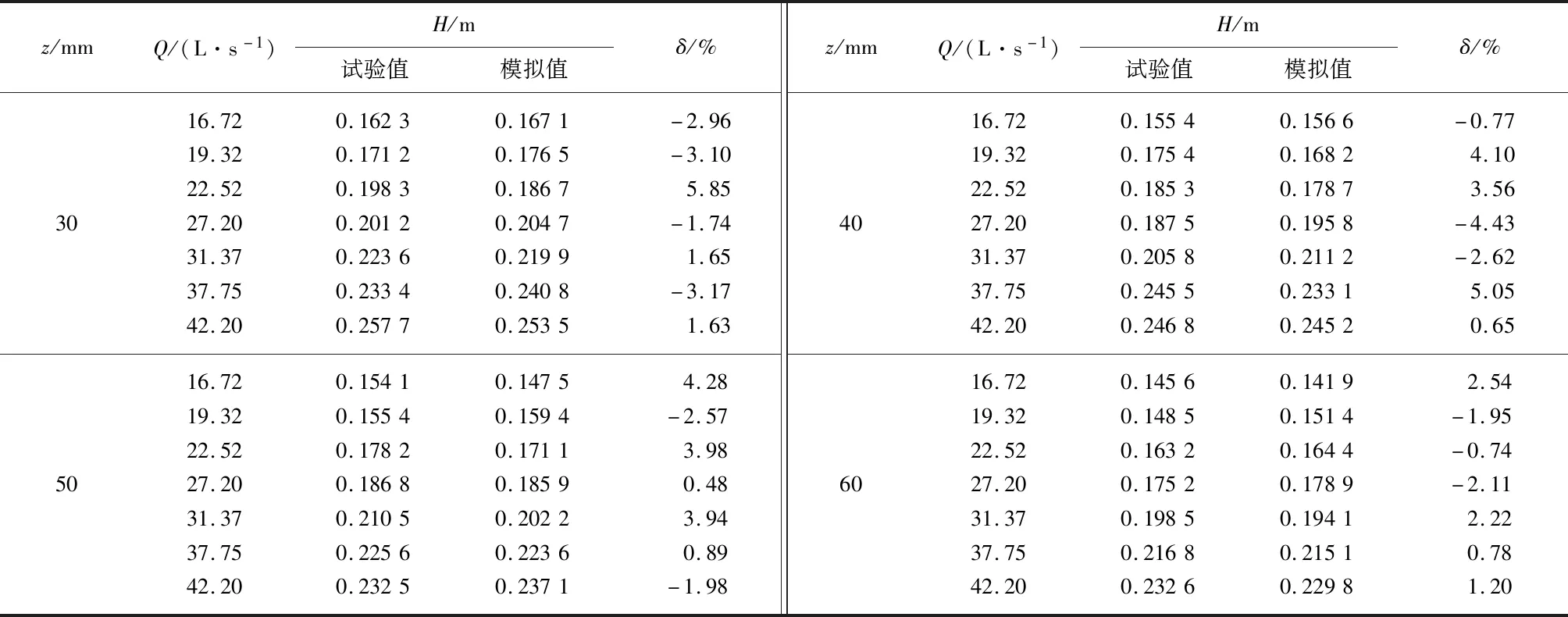
表2 试验值与模拟值对比Tab.2 Comparison of experimental and simulated values

4.2 孔口过流对堰上出流的影响

文献[15]表明：水流通过孔堰结构泄水建筑物时，会在建筑物的影响下，出现水体分层，分别从建筑物上、下通过，且上、下通过的流量之间会存在内部作用，相互影响.由图1b，1c对比可知，新型堰结构上相较于改进堰在底部增设了孔口，结构的差别会使原先改进堰的过流规律发生变化，为此需对新型堰的堰上过流规律进行研究.文中通过在Fluent软件中设置堰上的监测断面，以此获得了不同底孔高度、不同流量条件下的堰上过流量，将堰上断面的监测值与刘焕芳等[5]拟合出的改进堰公式计算值进行对比，如图5所示，图中δ为相对误差.

图5 堰上流量监测值与公式计算值对比图Fig.5 Comparison diagram of weir flow monitoring value and formula calculation value

从图5可以看出，不同孔口高度的新型堰在不同堰前总水头下堰上过流量监测值都略大于公式计算值，表明增设底部孔口后，孔口过流均促进了堰上过流；通过分析可知，从堰口溢出的水流在跌落的过程中有向下的速度分量，堰流在渠道下游与孔流汇合时，受孔流影响堰流的行进流速发生了变化，且孔流对堰流行进流速表现为一种促进作用，增大了堰上出流的行进流速，故流量增大.考察监测值与计算值的差值特征可知，其波动范围在0.61～2.45 L/s，并随着流量的增大差值逐渐减小，说明随着流量的增大，孔口过流对堰上过流的影响越来越小.

4.3 流速分布

在改进堰底部增设孔口后，孔口出流对堰上出流产生了促进作用，为更直观地表现孔口出流对堰上出流的影响，文中在Fluent软件中监测了沿矩形水槽中心纵剖面处x方向水流内部流速分布图及水面线，如图6所示.

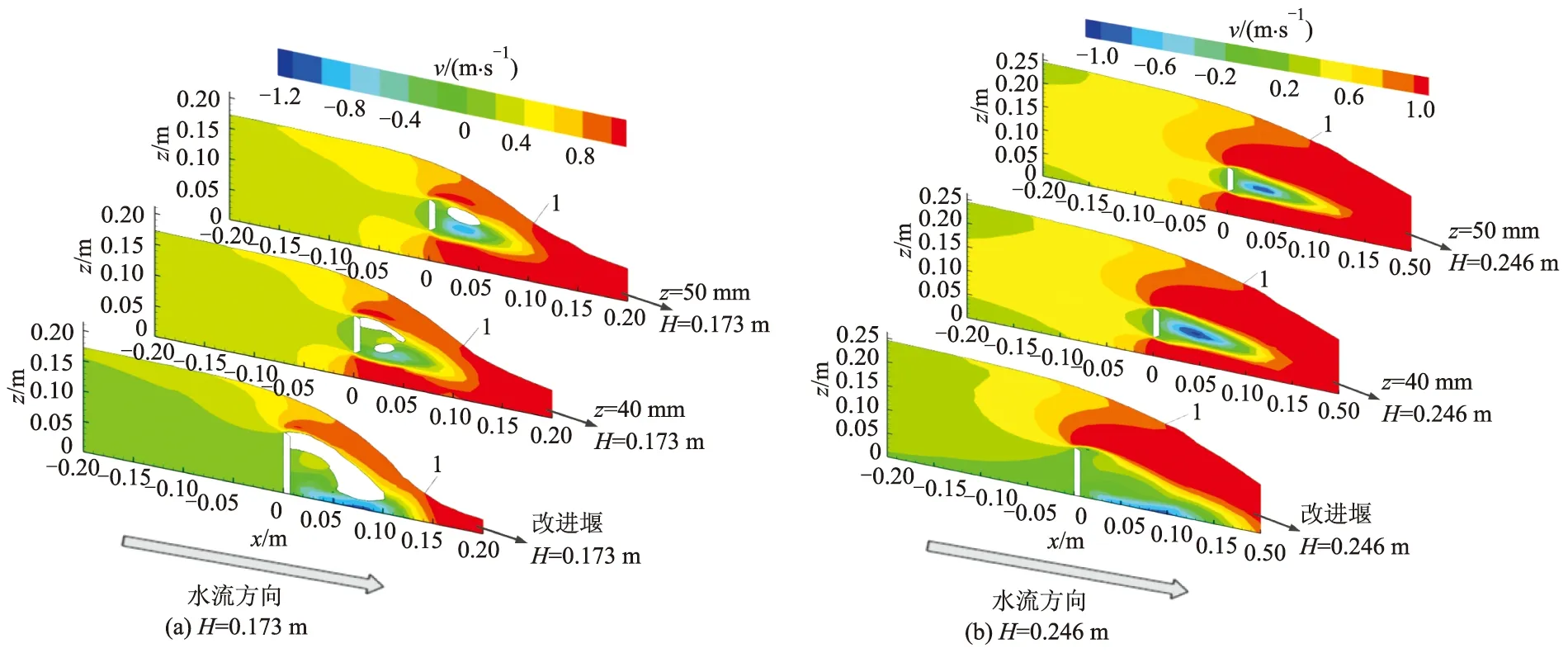
图6 水流沿x方向的流速分布图Fig.6 Flow velocity distribution diagram of water flow along x direction

由图6可知，水体从底孔通过时在其附近形成了特有的流场，改变了原先改进堰堰前底部水流沿x方向的流速分布，并在堰板前、后方与堰上水流均形成了掺混作用.由图6a模拟的结果对比可知，在堰板后方，掺混作用使堰上水流水舌内部的流速分布发生变化，见图中速度为1等值线的位置对比，流速分布的改变增加了堰上水流水舌的行进流速，在堰前水头不变的情况下，流量相应增加，可以看到在低水头情况下不同孔口高度的新型堰堰上监测值与计算值的相对误差均较大.

从图6b模拟的结果对比可知，在堰板后方掺混作用对堰上水流水舌内部的流速分布影响很小，如图中速度为1等值线的位置对比，由此可说明在高水头情况下，新型堰堰上水流与改进堰堰上水流的过流规律大致相同，可以看到高水头情况下不同底孔高度的新型梯形量水堰堰上流量监测值与公式计算值相对误差较小.通过监测图6b中改进堰、z=40，50 mm，速度为1等值线的位置可知，孔高为40，50 mm的新型堰孔流对堰流速度为1等值线的影响相较于改进堰分别增大了3%，9%，当以孔流对堰流的影响最小为条件，并考虑到新型堰的测流范围随着孔高的增大而增大时，文中推荐在堰顶宽b=250 mm的改进堰底部开设孔口50 mm形成新型梯形量水堰.

4.4 堰板两侧绕流

水流流经新型堰时，会因堰板的阻挡出现绕流，图7为z=40 mm，H=0.173 m的沿孔口长度方向不同位置的x方向的速度矢量图.

从图7可以看出，随着上游水流离堰板的距离越近，水流的绕流情况越明显，并在堰板上游附近出现了水流分流.

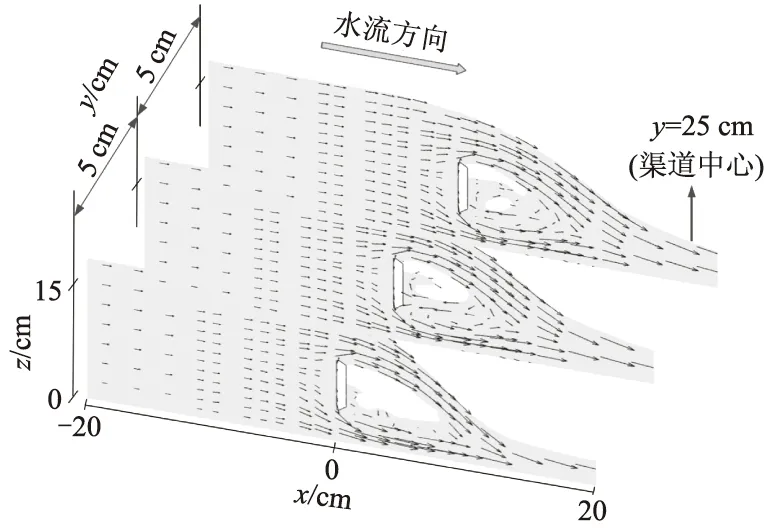
图7 速度矢量图Fig.7 Velocity vector diagram

4.5 综合流量系数

研究发现，综合流量系数m与h/z，H/z的关系最为显著，如图8所示.从新型堰结构可知，堰前总水头H=h+d+z，将其换算成H/z时，发现其比h/z多了一部分的尺寸效应(d，z)，由此使综合流量系数m与H/z的相关性较差，因此文中对综合流量系数m与h/z做了分析.

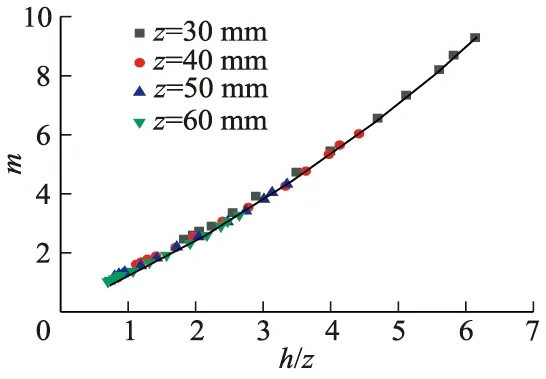
图8 综合流量系数m与h/z关系Fig.8 Relationship between combined flow coefficient m and h/z

由图8可知不同孔口高度的新型堰综合流量系数m随着h/z的增大而增大；对不同的h/z与计算出的综合流量系数进行拟合可知，其复相关系数达0.997.基于公式简单易用且通用性强的原则，得到了综合流量系数m与h/z的关系，并代入式(5)得到新型堰不同孔口高度下的测流公式，如式(12)所示，其适用范围:Q=[0.016,0.043] m3/s；b=250 mm；z=[30,60] mm；h=[0.04,0.17] m;P=100 mm.将不同底孔高度的不同堰前水头代入式(11)得到计算流量值，并与实测值对比，结果见表3.

(12)

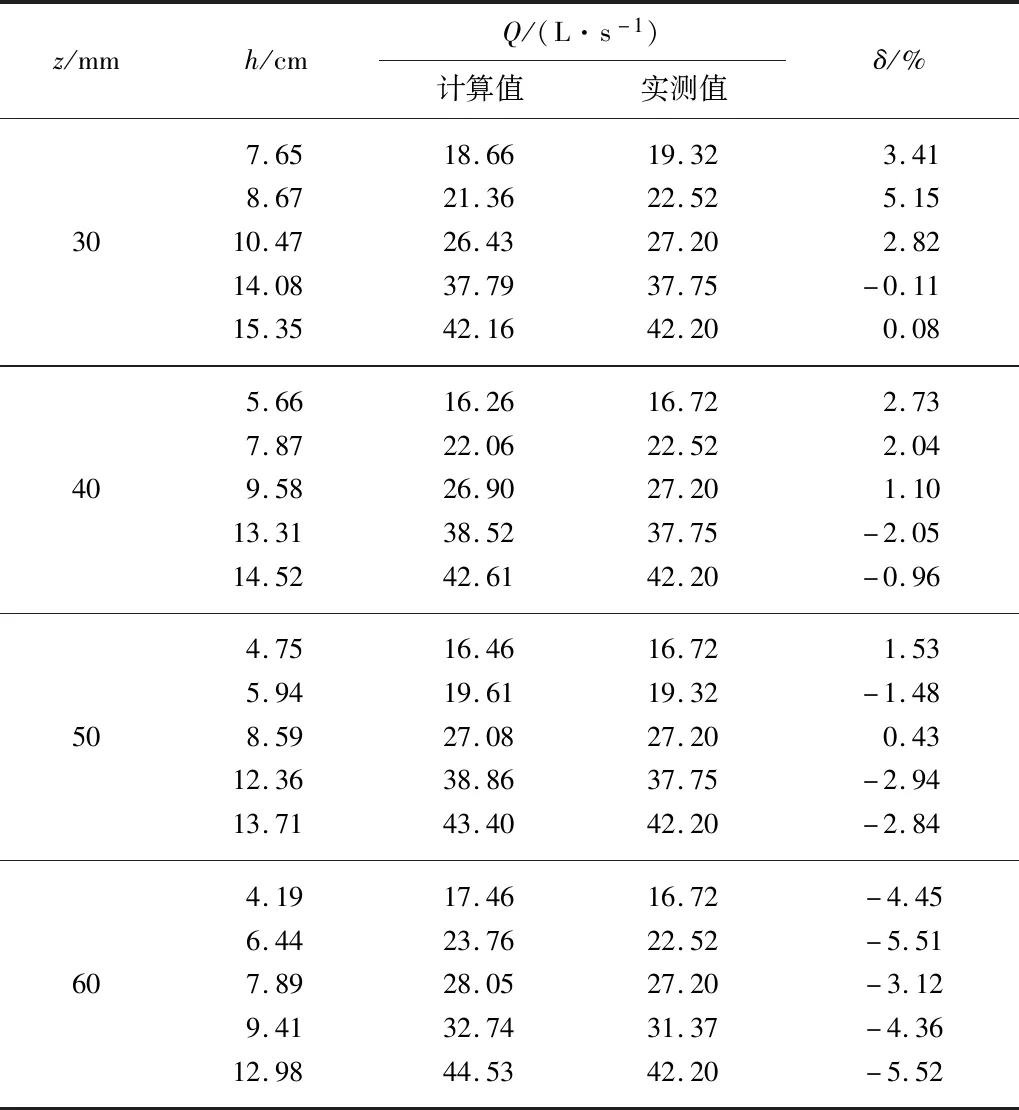
表3 实测流量值与计算流量值对比结果Tab.3 Comparison results between measured and calculated flow values

由表3 得知，式(12)的流量最大相对误差为5.52%，平均相对误差为2.63%，满足国家农业量水精度的要求；由于式(12)可计算不同孔口高度的新型堰流量，免去了因孔口高度不同，需重新率定综合流量系数的麻烦，公式的通用性较强.

对于b=250 mm的改进堰，可在堰板底部设置高为50 mm的矩形孔口形成新型堰，由表3知，采用式(12)计算其流量时，最大相对误差为2.94%，且最大过流流量较标准型扩大450%，较改进堰扩大32%，应用范围提升幅度较高，可应用于生产实践中.

5 结 论

1) 基于量纲一化分析原理，得到新型堰流量公式的基本型式，对所得数据进行分析并拟合出了综合流量系数的表达式，得到的测流公式平均相对误差为2.63%，满足国家农业量水精度的要求，且公式的通用性较强.

2) 通过对不同底孔高度、不同流量条件下的新型堰堰前水头模拟值与监测值进行对比可知，两者结果最大相对误差为5.85%，模拟结果可信度高，可以保证准确性.通过分析水流沿x方向内部的速度分布，获得了不同堰前水头、不同孔口高度条件下孔口出流对堰上出流的影响规律.

3) 考虑梯形量水堰在灌区量水中存在测流范围小等问题，可在b=250 mm改进堰的基础上，在底部增设高为50 mm的孔口形成新型堰，其测流范围更广，并具有良好的防淤效果，最大相对误差为2.94%，完全满足灌区对量水精度的要求.

4) 新型堰结构简单、测量方便，相比于同条件下的改进堰应用范围更广.