基于HJC损伤本构模型的灰岩隧道光面爆破数值模拟及工程验证❋

秦桂芳 曾 灿 徐间锋 贺 睿

①贵州路桥集团有限公司(贵州贵阳，550000)

②中南大学土木工程学院(湖南长沙，410075)

引言

近年来，我国高速铁路规模越来越大[1]。作为高速铁路的一个重要组成部分，隧道的数量和长度均在逐渐增大。在隧道爆破施工中，爆破方案的选择决定了隧道爆破开挖成型效果的好坏，进而影响隧道的掘进成本和开挖效率[2-3]。因成本低、效率高、灵活性好等优点，钻爆法被广泛运用于隧道施工作业中[4-5]。陈学松等[6]通过优化现场孔网参数，控制了爆破块度，降低了炸药的单耗。王圣涛等[7]在施工现场进行了多次空间间隔光面爆破试验，不断优化爆破参数后，提出了适合的爆破方案。岳中文等[8]利用试验和数值模拟的方法分析了在不同不耦合系数下混凝土的爆破漏斗，发现存在最佳的不耦合系数，此时能尽可能地利用炸药的能量；杨哲峰等[9]针对武汉地铁二号线工程，通过分析关键节点上的有效应力规律，确定出最佳的径向不耦合系数。张理维等[10]发现，炮孔连线间岩体的损伤程度随炮孔间距的增大而减小，损伤区由贯通变为不贯通。蔡峰等[11]利用Matlab编程和弹性理论求解了冲击波初始参数和沿爆破孔径向传播到爆破孔孔壁处的参数；并利用数值计算和现场试验验证了结果的正确性。

隧道爆破效果受装药结构、岩体性质等多种因素的影响[12-13]，相关参数变异性大，作用机理复杂，尚缺乏可直接借鉴应用的系统性成果。而盲目套用既有研究成果很可能会导致爆破效率低或材料浪费等现象。根据前人的研究成果发现，周边眼设计参数优化是实现隧道爆破控制最为有效的方法之一[14]。为保证六枝至安龙高速公路隧道的顺利施工，现针对灰岩的爆破效果开展研究，分析周边眼不同的径向不耦合系数、炮孔间距对硬岩光面爆破的影响，并结合现场情况对所提出的方案进行了验证。

1 工程概况

六枝至安龙高速公路隧道项目地处贵州高原西部。场区属溶蚀地貌单元，海拔介于938.9～1 414.5 m。隧道轴线通过段海拔为1 029.1～1 414.5 m之间。进口端为陡坡地形，自然坡度为40°～50°；洞身段穿越山脊，最高点处海拔为1 414.5 m；出口端为陡坡地形。洞身穿越地层主要为III级中风化灰岩。隧道按照时速80 km的标准进行设计。

原设计采用全断面施工，循环进尺2 m，每循环装药炮眼总数229个。前期施工发现，该爆破方案存在炮眼总数过多(每循环炮眼钻设耗时3～5 h)、炸药用量过大(单耗超过2 kg)、超挖严重(平均超挖量超过30 cm)等现象。因此，综合分析后，采用钻爆法施工。

2 基于显示动力学的爆破模拟方法

2.1 基本思路

隧道钻爆法施工过程中，周边眼合理的装药结构能有效地减小超挖量和欠挖量。为此，基于显示动力学ANSYS/LS-DYNA软件，将周边眼爆破时对围岩的冲击作用简化为二维尺度下的平面应变问题，并从损伤控制的角度，提出适用于六枝至安龙高速公路隧道的周边眼装药参数。

具体思路为:

1)改变周边眼单孔装药的径向不耦合系数，建立多种工况，对比分析得到合适的径向不耦合系数取值区间；

2)根据初拟定的径向不耦合系数建立周边眼双孔爆破模型，探讨不同炮孔间距下的爆破破岩效果，总结出合适的炮孔间距取值范围；

3)建立精细化隧道爆破数值模型，并对爆破效果做出评价；

4)将初始拟定的周边眼爆破参数应用于爆破现场，并分析爆破效果。

2.2 材料本构模型及参数

为模拟炸药瞬时爆炸产生的巨大能量使岩石处于大 应 变、高 应 变 率 的 状 态，岩 石 采 用HJC(Holmquist-Johnson-Cook)动态本构模型[15]，屈服方程为

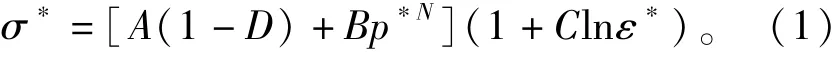
式中:σ*为标准化等效应力，为实际应力与静态抗压强度的比值；p*为标准化静水压力，为实际静水压力与静态抗压强度的比值；ε*为无量纲应变率，为实际应变率与参考应变率的比值；D为损伤变量；A、B、N和C为试验后确定的常数。

爆破载荷作用下，岩石的损伤演化方程为

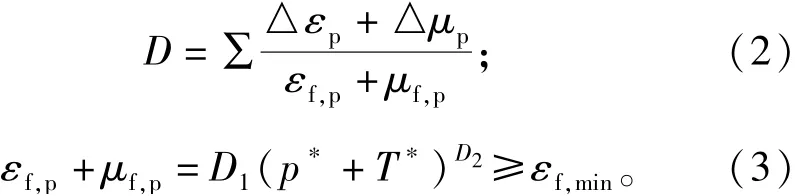
式中:△εp、△μp分别表示岩石在一个计算循环内的等效塑性应变和塑性体积应变；(εf，p+μf，p)表示常压下岩石断裂时的塑性应变；T*表示岩石所能承受的最大特征化静水拉力；D1、D2为损伤常量；εf，min为岩石断裂时的最小塑性应变。

爆破载荷作用下，岩石的状态方程包括线弹性、过渡和压密3个阶段。压密阶段的状态方程为

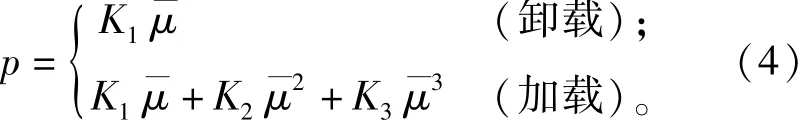
式中:K1为塑性体积模量；K2和K3为材料的压力常数；μ为修正后的体积应变。

结合现场地质勘察报告和经验取值，选定岩石的HJC本构模型参数，见表1。

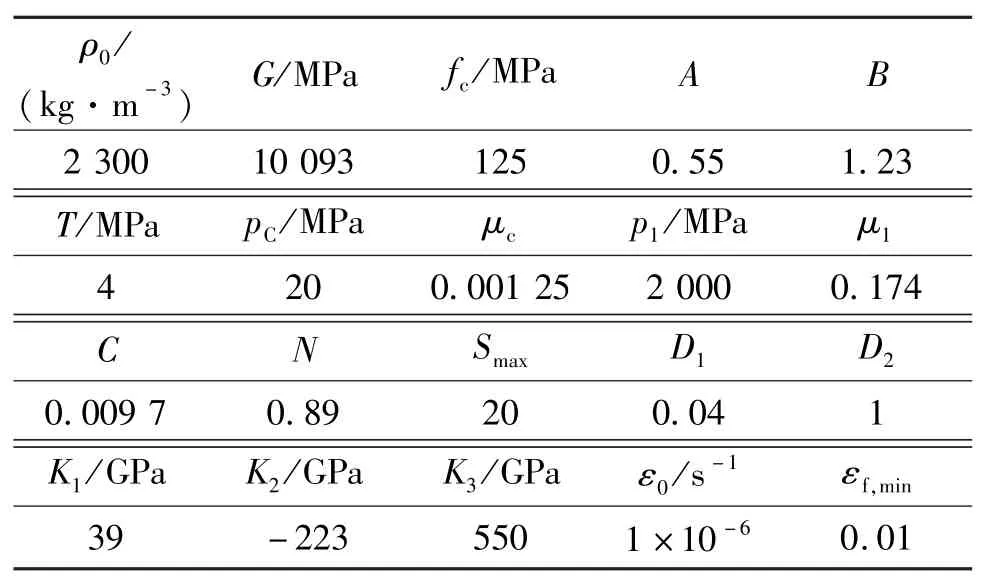
表1 岩石HJC本构模型参数Tab.1 Parameters of HJC constitutive model of rock

炸药选用常用的2＃岩石乳化炸药，材料模型为*Mat_High_Explosion_Burn，状态方程为

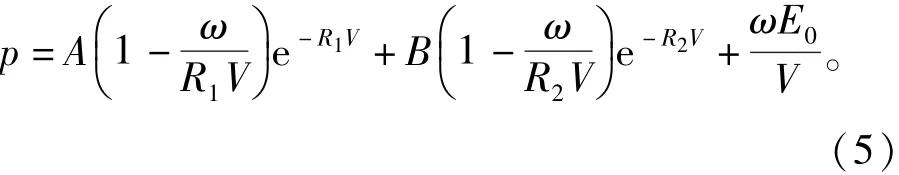
式中:p为爆轰压力；V为相对体积；E0为初始比内能；A、B、R1、R2、ω为常数。

炸药材料参数见表2。

表2 2＃岩石乳化炸药材料参数Tab.2 Material parameters of 2＃rock emulsion explosive

空气采用线性多项式状态方程*Eos_Linear_Polynomial进行描述:

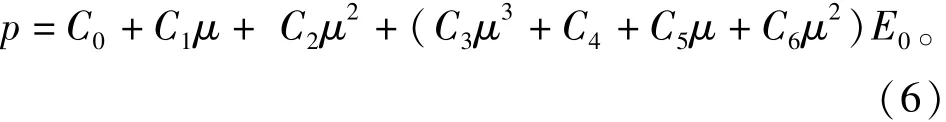
式中:C0~C6为常数；μ为体积比。

空气材料参数见表3。

表3 空气材料参数Tab.3 Material parameters of air

2.3 计算工况

主要分析了径向不耦合系数和炮孔间距等对爆破效果的影响。为方便计算，模型采用厚度为一个单元尺寸的准三维薄片性计算模型。

1)在分析径向不耦合系数对爆破效果的影响时，岩体采用单孔爆破。如图1所示，模型直径为100 cm，炮孔位于模型中心位置，药卷直径为3.2 cm。通过改变炮孔直径，设定径向不耦合系数kd分别为1.00、1.15、1.25、1.50和1.75共5个工况。

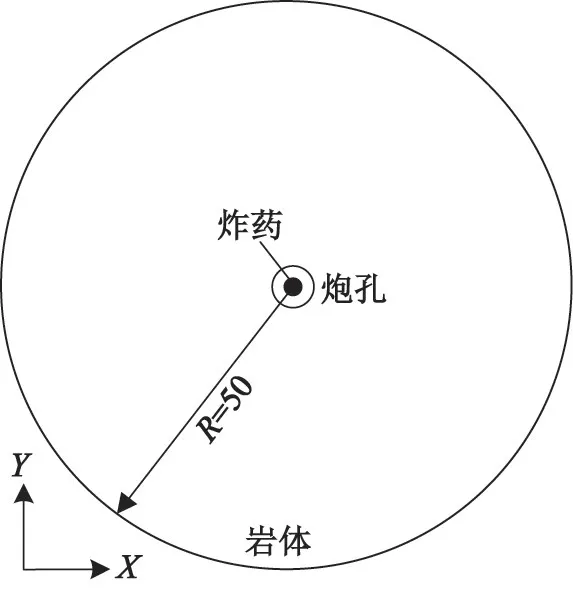
图1 单孔爆破模型(单位:cm)Fig.1 Single-hole blasting model(unit:cm)

2)在分析炮孔间距对爆破效果的影响时，岩体采用双孔爆破。如图2所示，模型尺寸为300 cm×300 cm，炮孔在模型中呈左右对称布置并设置中心起爆，药卷直径为3.2 cm。径向不耦合系数由图1中分析得到。保持径向不耦合系数不变，设定炮孔间距分别为45、50、55 cm和60 cm 4种工况。

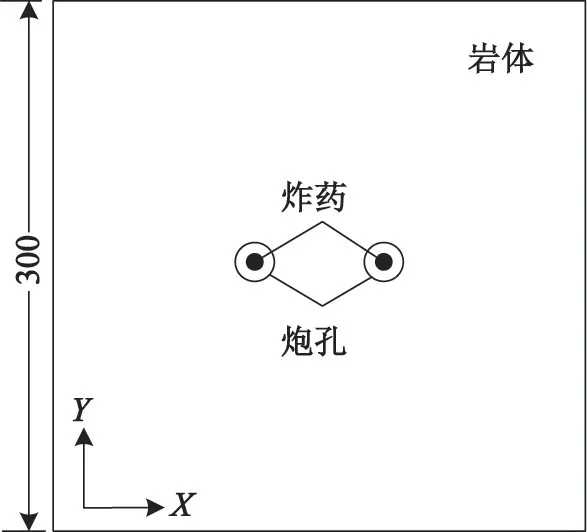
图2 双孔爆破模型(单位:cm)Fig.2 Double-hole blasting model(unit:cm)

3)以选定的径向不耦合系数和炮孔间距，建立隧道上台阶爆破开挖精细化爆破数值模型。模型的整体尺寸为1 500 cm×800 cm，周边眼共33个，光面爆破层厚度为70 cm，如图3所示。

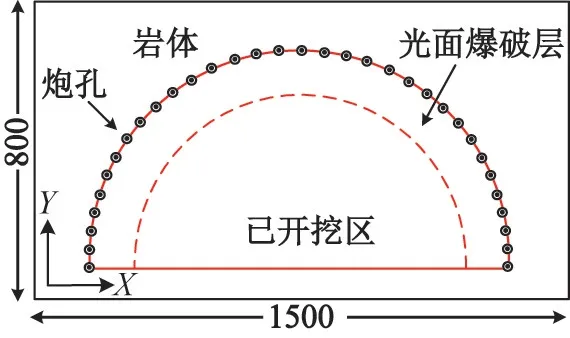
图3 爆破模型(单位:cm)Fig.3 Blasting model(unit:cm)

模型中，岩石采用Lagrange网格建模，单元类型为3D Solid 164，使用Lagrange算法。炸药和空气采用ALE网格建模，单元类型为3D Solid 164，使用多物质算法。岩石与炸药和空气之间的相互作用通过定义耦合算法来实现。模型的左、右两侧边界分别施加X向位移约束，上、下两侧边界分别施加Y向位移约束，厚度方向施加位移约束，四周添加无反射边界条件。

3 基于HJC本构模型的岩体损伤演化特征分析

3.1 单孔爆破岩体损伤特征

图4给出了当径向不耦合系数为1.00时，炸药起爆后灰岩的损伤变量D随计算时间的演化情况。图5给出了径向不耦合系数kd分别为1.00、1.15、1.25、1.50和1.75时岩体的损伤云图。

图4和图5中，红色区域代表完全损伤区(压碎区)，损伤变量D＝1.00；蓝色以外的灰色区域代表无损伤区(弹性区)，D＜0.05；介于红色与蓝色之间区域的是损伤区(裂隙区)，0.05＜D＜1.00[16]。

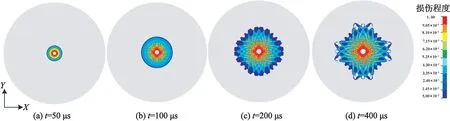
图4 径向不耦合系数为1.0时单孔爆破下灰岩的损伤演化图Fig.4 Damage evolution of limestone in single-hole blasting with radial decoupling coefficient of 0.1

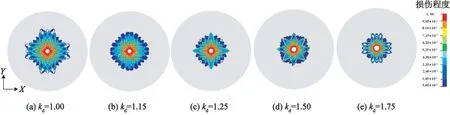
图5 不同径向不耦合系数下岩体的损伤云图Fig.5 Damage nephograms of rock mass with different radial decoupling coefficients

分析可见:

1)炸药起爆后，应力波以柱面波的形式向四周扩散传播。冲击载荷压力先作用在炮孔孔壁上，形成压碎区；衰减的应力波对压碎区之外的岩体产生切向拉伸力，形成放射状的径向裂隙区；在破裂区之外，应力波已衰弱，只能引起岩体的弹性振动，而不能破坏岩体，此区域即为弹性区。

2)在不同的径向不耦合系数下，岩体的损伤分布规律很相似，都呈现交叉放射絮状，由中心向外部扩展。

为更加清晰地剖析爆破作用下的破岩机理，分别在不同工况下提取炮孔附近岩体的孔壁压力p。从图6可知:炮孔孔壁压力随径向不耦合系数kd的增大而减小；当kd＜1.25时，孔壁压力变化较显著；当kd＞1.25时，孔壁压力变化较平稳。

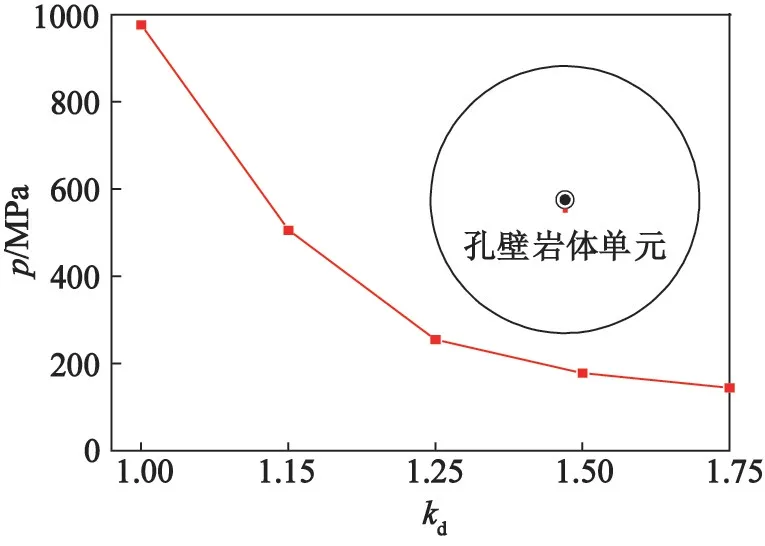
图6 孔壁压力与径向不耦合系数的关系Fig.6 Relationship between hole wall pressure and radial decoupling coefficient

为定量地探讨爆破作用下岩体损伤的空间分布规律，分别在各个工况下，提取沿同一爆心距R圆周上间隔10°的岩体单元，以其算术平均值来表征该爆心距下的岩体受爆破作用的损伤程度，如图7所示。从图7可知:kd＝1.00时，压碎区和裂隙区半径分别为13 cm和40 cm；kd＝1.75时，压碎区和裂隙区半径分别为7 cm和36 cm。因此，合理地增大径向不耦合系数，能够有效地减少炮孔周围的损伤。

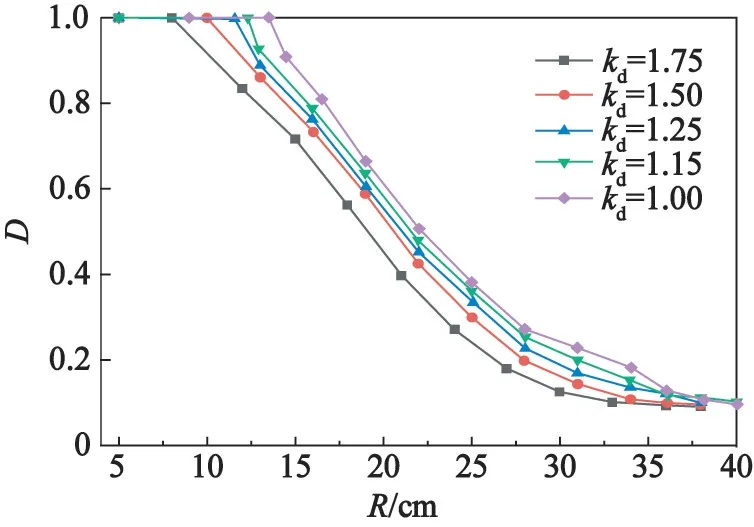
图7 岩体损伤变量与爆心距的关系Fig.7 Relationship between damage variable of rock mass and blasting center distance

综合分析结果和现场施工器械的可操作性，拟定炮孔直径为4 cm，径向不耦合系数为1.25。这样既一定程度上降低了围岩的损伤程度，也提供了足够大的孔壁压力，保证了破岩效果。

3.2 双孔爆破岩体损伤特征

隧道周边眼光面爆破的炮孔间距一般设定在40 cm以上。由单孔爆破数值模拟结果可推知，周边眼单孔爆破的损伤仅能影响相邻炮孔区域。因此，开展双孔爆破岩体损伤特征分析。

图8给出了炮孔间距依次为45、50、55 cm和60 cm 4种工况下的岩体损伤云图。分析可知:双孔爆破时，岩体的损伤分布和单孔爆破时的损伤演化规律类似，都呈交叉放射状向外扩散；炮孔之间的岩体受爆破应力波的叠加作用，形成较大的压碎区；炮孔连线中心岩体单元主要受到拉伸破坏。

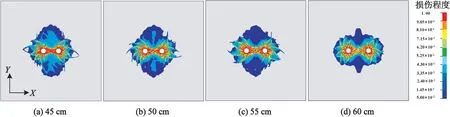
图8 不同炮孔间距下岩体的爆破损伤演化图Fig.8 Blasting damage evolution of rock mass with different blast hole spaces

图9是炮孔中心测点岩体单元的拉应力峰值与炮孔间距的关系。凝灰岩的抗拉强度σt＝4 MPa。岩体的动态抗拉强度是静态时的1～10倍，这里取定灰岩的动态抗拉强度σt为16 MPa。

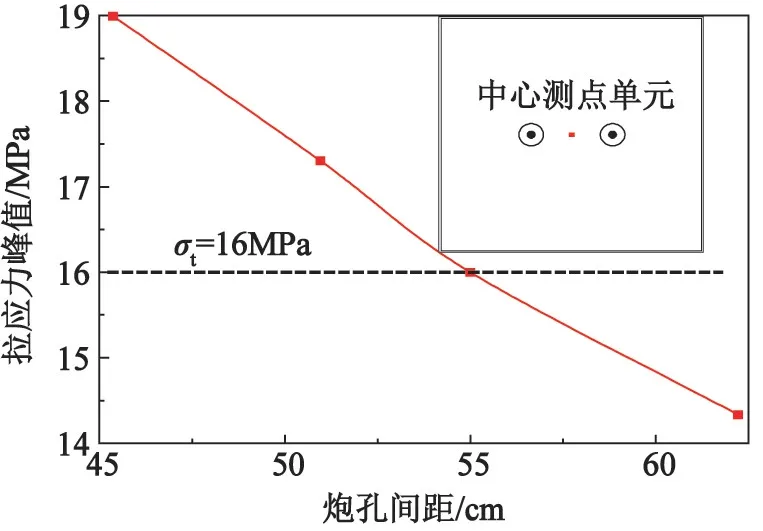
图9 测点拉应力峰值与炮孔间距的关系Fig.9 Relationship between peak tensile stress at measuring points and blast hole space

由图9可知，随着炮孔间距的增大，中心测点单元的拉应力峰值逐渐减小，且当炮孔间距大于55 cm时，中心测点单元达不到动态抗拉强度。以D＞0.05来界定岩体受到爆破作用的影响，提取各个炮孔间距下在X(炮孔中心连线)、Y(垂直炮孔中心连线)方向上的最大损伤长度，如图10所示。

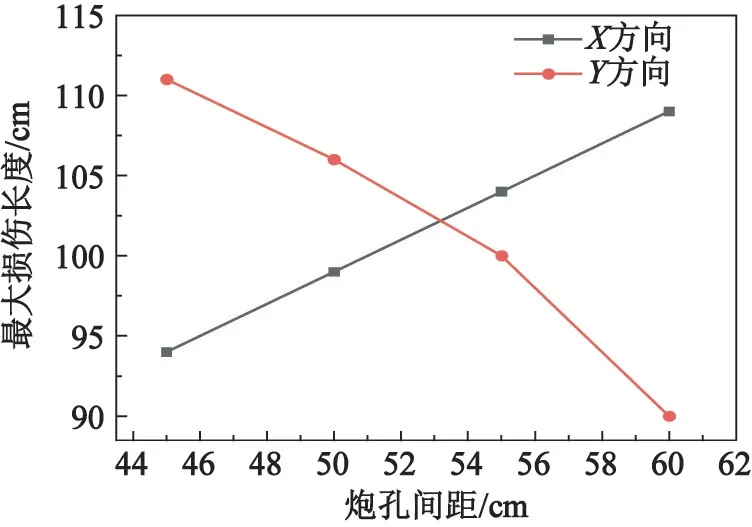
图10 最大损伤长度与炮孔间距的关系Fig.10 Relationship between maximum damage length and blast hole space

由图10可知:当炮孔间距增大时，沿着X方向的损伤长度逐渐增大；沿着Y方向的损伤长度逐渐减小。因此，在隧道周边眼爆破时，炮孔间距的大小会影响当前爆破掌子面的径向损伤范围。为保证足够的爆破破岩效果，也尽量降低围岩的损伤范围，拟定炮孔间距为55 cm。

3.3 隧道爆破成型效果数值模拟

周边眼径向不耦合系数为1.25、周边眼间距为55 cm、光面爆破层厚度为70 cm时，隧道光面爆破的数值模拟效果见图11。

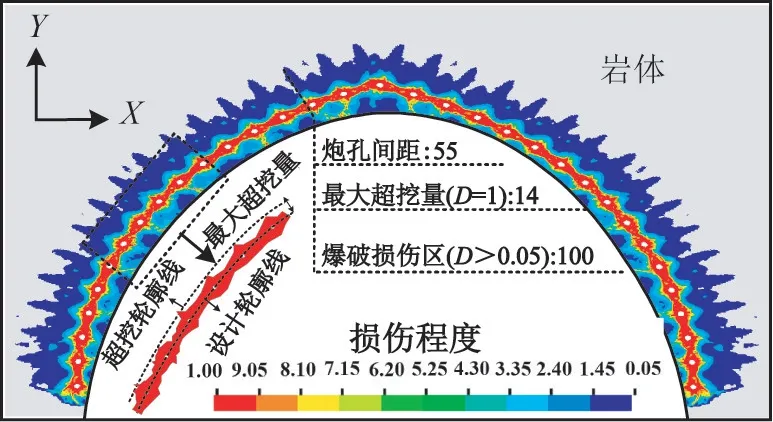
图11 隧道光面爆破的数值模拟效果图(单位:cm)Fig.11 Numerical simulation outcome of smooth blasting of tunnel(unit:cm)

与隧道爆破成型效果直接相关的因素是隧道的超挖和欠挖。根据《锚杆喷射混凝土支护设计施工规定》，爆破方式采用光面爆破时，平均线性超挖应小于15 cm。

式中:△S为超挖面积，m2，由数值模拟结果得△S＝1.51 m2；L为隧道断面设计周长，m，取L＝18.84 m；△R为平均径向超挖差，m。

由数值模拟结果可知，平均径向超挖差△R为8 cm。由此可以判定，当光面爆破层厚度为70 cm时，径向不耦合系数取1.25、炮孔间距取55 cm是可行的。

4 工程应用

将上述推荐参数应用于六枝至安龙高速公路隧道III级灰岩段的现场爆破，爆破效果如图12所示。可以看出，爆破参数优化后，轮廓线平整，极大地减少了局部的超挖和欠挖，降低了造价，既达到了良好的爆破开挖效率，同时也控制了岩体振速，使隧道爆破对周边环境的影响在允许范围内。爆破结束后形成的隧道开挖轮廓线与设计轮廓线基本吻合，说明设定的爆破参数是合理的。

图12 爆破效果Fig.12 Blasting outcomes

5 结论

为提高硬质灰岩地层隧道爆破开挖效果，基于显示动力学中的HJC损伤本构模型，通过有限元数值模拟方法分析了周边眼径向不耦合系数、炮孔间距对隧道爆破效果的影响，得出的主要结论如下:

1)单孔爆破工况中，炮孔孔壁压力随径向不耦合系数的增大而减小；炮孔周围围岩的损伤程度随径向不耦合系数的增大而减小。

2)双孔爆破工况中，当炮孔间距增大时，沿着X方向的损伤长度逐渐增大；沿着Y方向的损伤长度逐渐减小。

3)基于数值模拟结果，优化得到适用于工程应用的爆破参数，即:径向不耦合系数为1.25，炮孔间距为55 cm。该爆破参数应用于现场后，隧道轮廓线平整，爆破形成的隧道开挖轮廓线与设计轮廓线基本吻合，应用效果良好。

采用的爆破损伤模型及计算方法可以为类似工作提供一定的参考。但隧道光面爆破效果与其他诸多爆破参数(光面爆破层厚度、装药量、炮孔孔径、起爆时差等)的设定有关，高应力条件下各爆破参数对岩体爆破损伤的影响还需要进一步研究。同时，应加强对光面爆破成型现场的监测，实时合理地调整爆破参数。