带有随机网络时延的H∞模糊控制的偏差界依赖设计

马明，张丽娟，孟莹梅

（江苏城市职业学院，江苏南通，226006）

0 引言

网络化控制系统 (NCSs) 具有资源共享、低成本、高可靠性和远程控制等优点[1]。网络诱导时延会在对象与控制器之间的信息交互时产生，它们会破坏[2,3]或改善[4]系统稳定性和性能。网络诱导时延通常表现时变或者随机特征[5]。如何充分利用网络诱导时延的特征建模、分析和设计NCS是非常重要的课题，分别针对线性NCS[6-9]和基于T-S模糊模型的NCS[10]已有一些文献报道。

文献[10-12]研究了基于网络的T-S模糊系统的模糊控制，但假设模糊控制器依赖于连续检测的前件变量，必然增加执行成本。文献[13-17]去掉了这个假设，构造了一类依赖于可利用离散前件变量的模糊控制器，将带有网络诱导时延的基于T-S模糊模型的NCS建模成具有区间时变时延的异步 T-S模糊系统。然而，文献[13,14]忽略了T-S模糊模型和模糊控制器的前件变量的异步运行特征，导致设计结果非常保守[15]。文献[16,17]引入了异步归一化隶属度函数的偏差界，但是文献[16,17]引入许多松弛矩阵变量，计算量过大，本文将考虑网络诱导时延的随机特征以及T-S 模糊模型和网络化模糊控制器的异步运行特征，研究网络化模糊H∞控制问题，主要贡献如下：

（1）利用伯努利分布刻画网络诱导时延的随机特征, 构造一类依赖于离散前件变量和采样状态的网络化模糊控制器，建模一个具有两个分段区间时变时延和随机参数的异步T-S模糊系统。

（2）利用偏差界和归一化隶属度函数的凸性，建立了异步系统的H∞性能分析和控制器设计的新颖时滞依赖判据。

（3）证实了所提方法比现有方法具有较低的计算复杂度，且具有较低的保守性和计算复杂度。

1 预备知识

文中的数学符号定义如下：sym{X} =X+XT，ε表示数学期望，*表示对称诱导项，⊗表示Kronecker积，L2[0,∞)表示定义域为[0,∞)上的均方可积函数。

2 问题描述

本文考虑的系统框架如图1所示，模型描述如下：

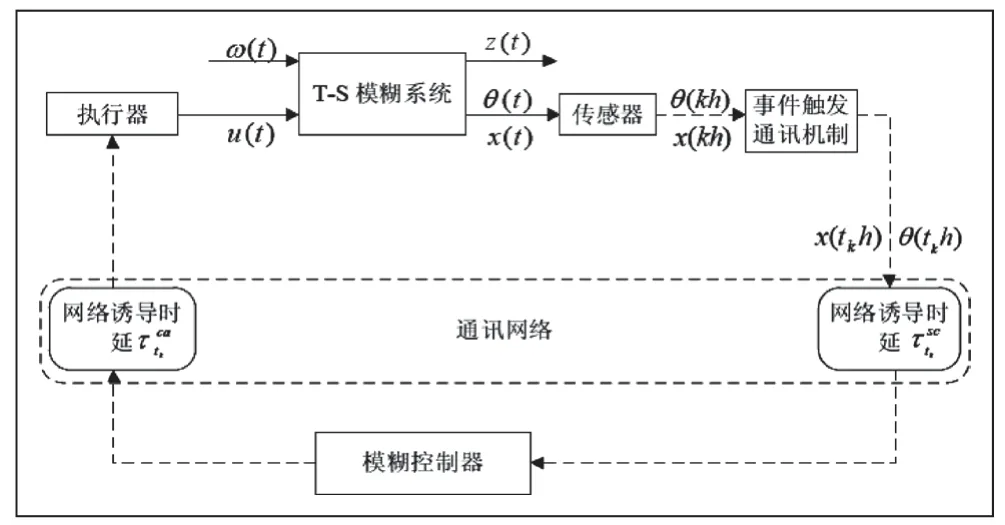
图1 事件触发通讯机制下的T-S模糊系统的控制框架

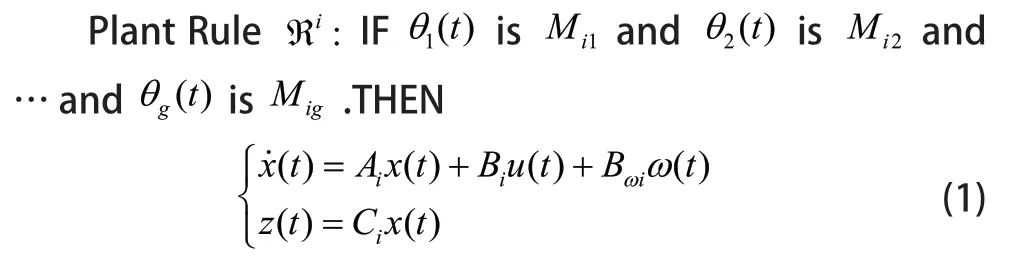
其中i= 1,2,...,r，r是IF-THEN规则数目：x(t) ∈ℝn,u(t) ∈ℝm,z(t) ∈ℝp,ω(t)∈ℝl分别是系统的状态向量，控制输入，被控输出和外部干扰输入且ω(t) ∈L2[0,∞);Ai,Bi,Bωi,Ci为适当维数的定常矩阵；Mij(i= 1,2,...,r;j= 1,2,...,g)为模数集，前件变量θ(t)=[θ1(t) ,θ2(t),...,θg(t)]T是关于x(t)的函数并且不依赖于u(t)。系统（1）的初始状态为x( 0)=x0。系统（1）的全局模型可描述为：

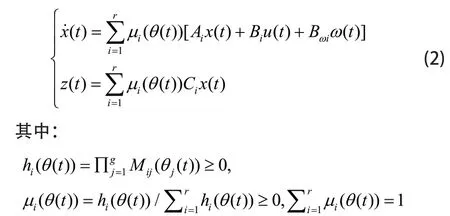
模糊系统（1）的采样信号θ(kh)和x(kh)(k∈ℕ)经事件触发器筛选后到模糊控制器，其事件触发算法如下：

满足：

因此，本文的研究目标是设计控制器（4）使得闭环系统（8）达到均方意义下随机稳定的并具有一定的H∞性能，即：

3 模糊H∞性能分析和控制器设计

本节主要研究系统（8）的模糊H∞性能分析和控制器设计的时滞依赖判据，描述如下：

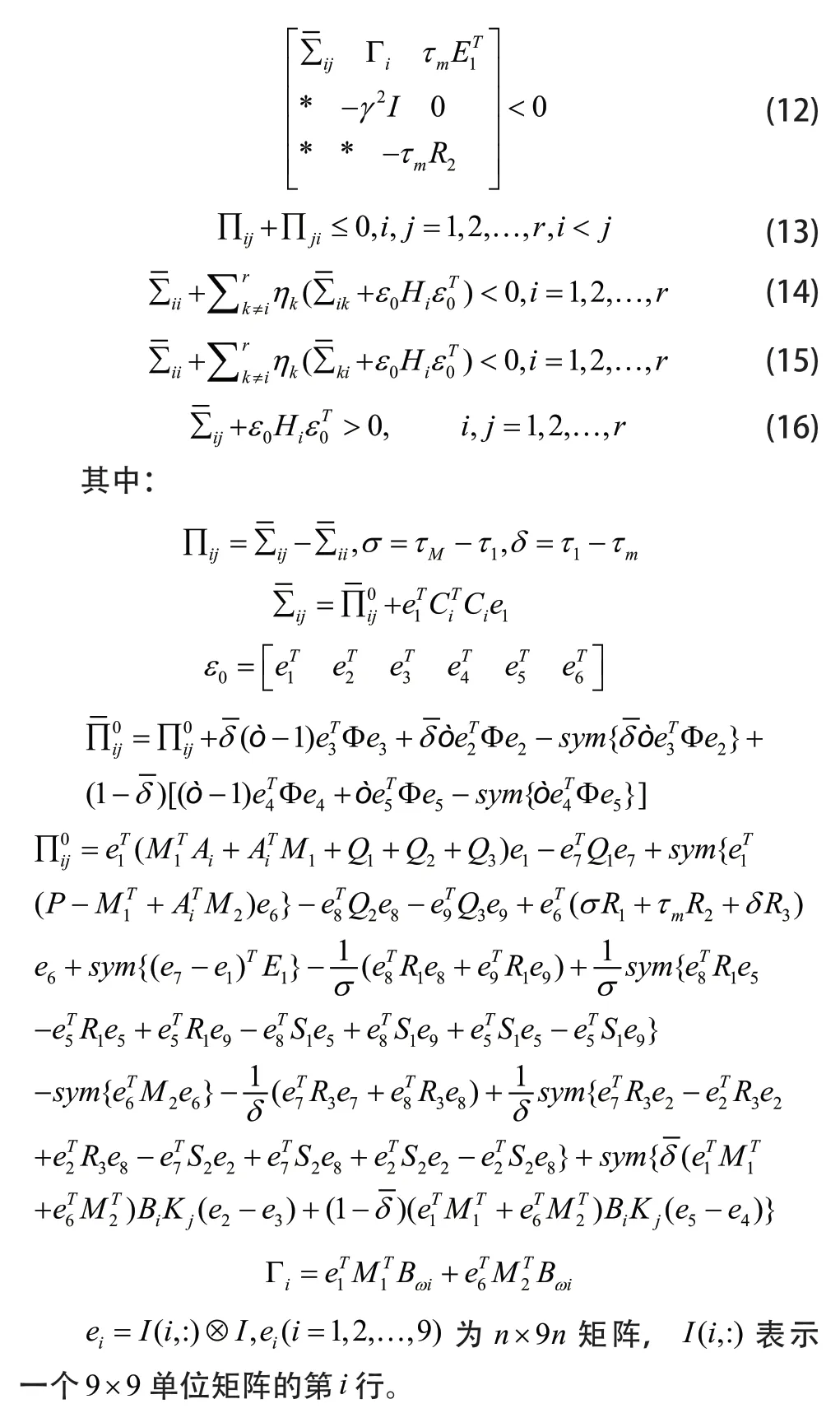
证明 构造以下Lyapunov-Krasovskii泛函：

接下来，我们证明具有ω(t)=0的系统（8）在均方意义下是随机稳定的。对任意具有适当维数的矩阵 M1和 M2，当ω(t )=0, t ∈Ωl,k时，以下等式成立：

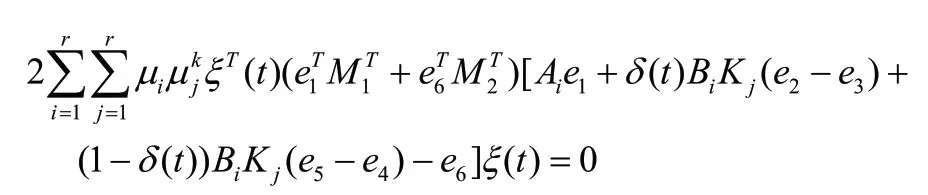
由文献[18]中的引理1和文献[19]中的引理1可知，若（10）-（11）成立，则：

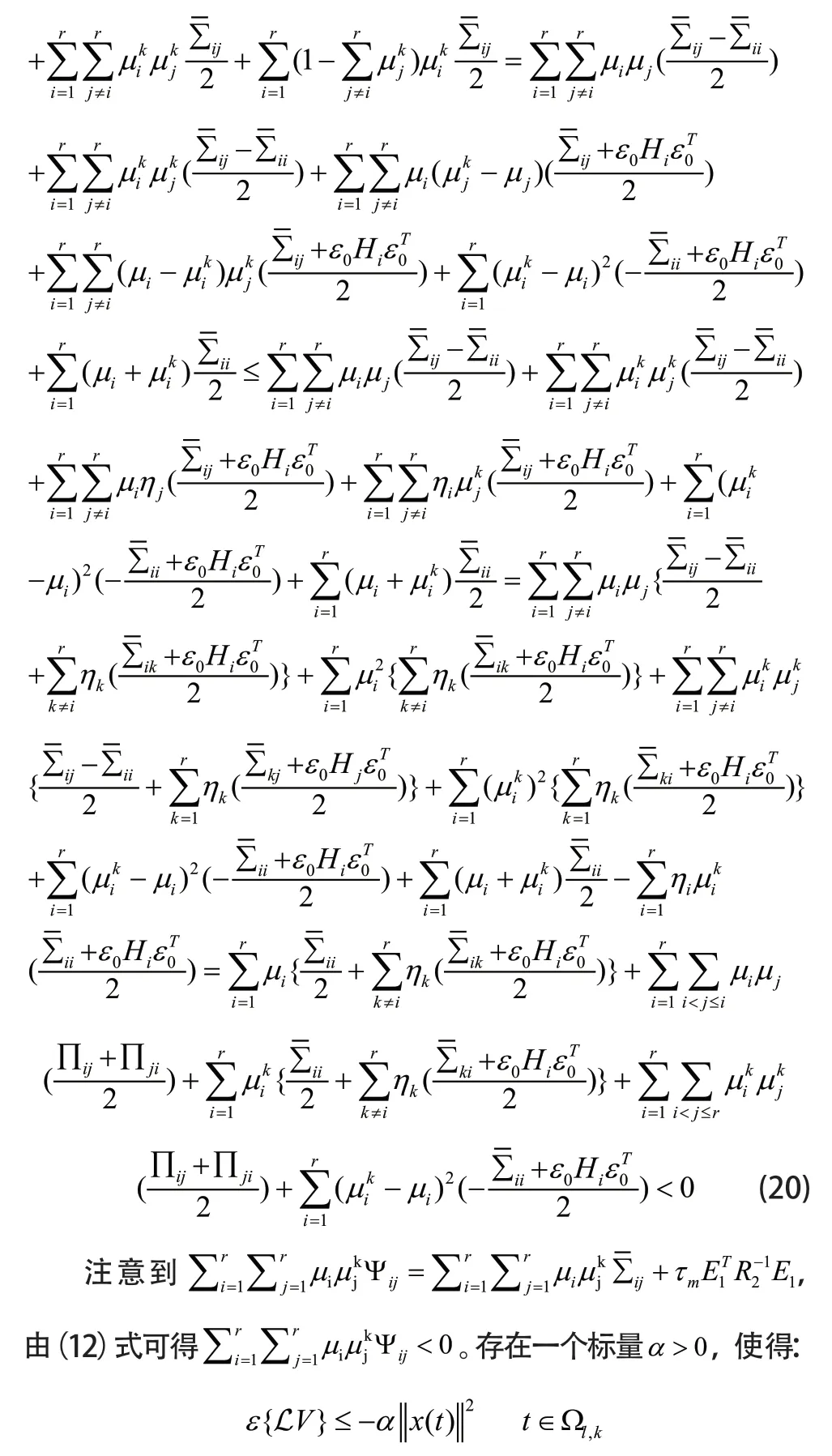
这就表明具有()0tω=的模糊系统（8）在均方意义下是随机稳定的。

下面，我们证明在零初始条件下，对任意非零的ω(t ) ∈ L2[0,∞]，闭环系统（8）具有给定的H∞性能γ，利用（17）式可得：

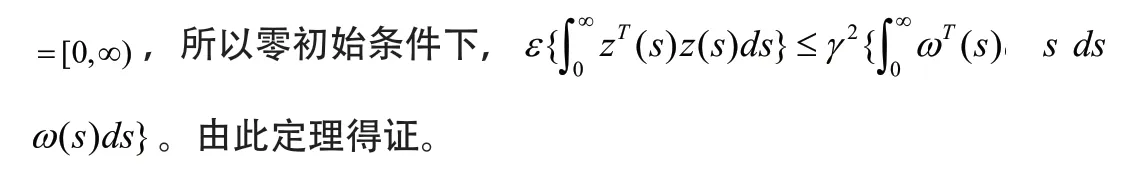
注2：从定理1的证明可以看出，我们建立了异步T-S模糊系统的H∞性能判据。而现有文献[16,17]的主要结论没有考虑网络诱导时延的随机特征，且增加计算复杂度和引入保守性。

下面给出基于LMI的控制器设计判据。

4 仿真例子

考虑以下非线性弹簧-质量-阻尼系统[16]：

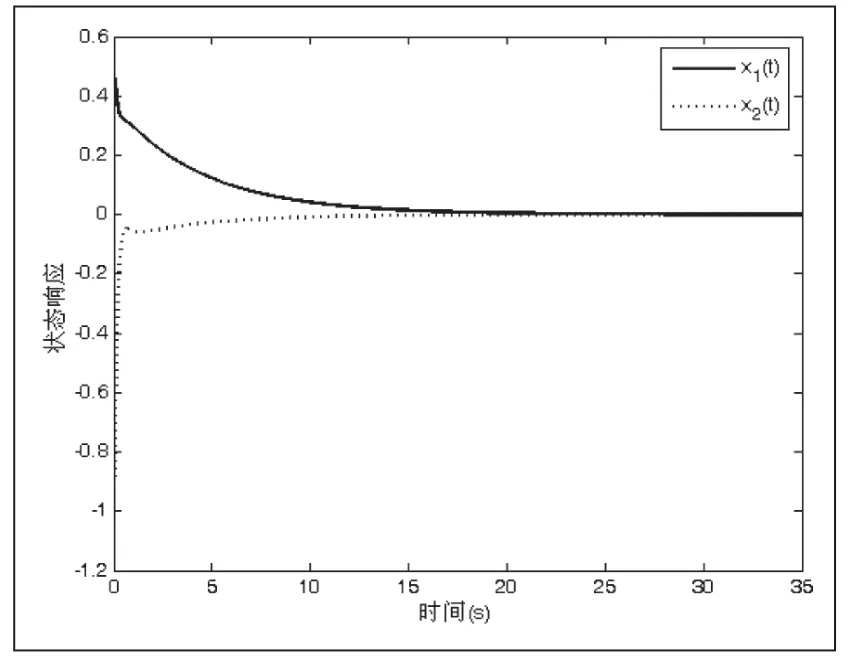
图2 系统（31）的状态响应

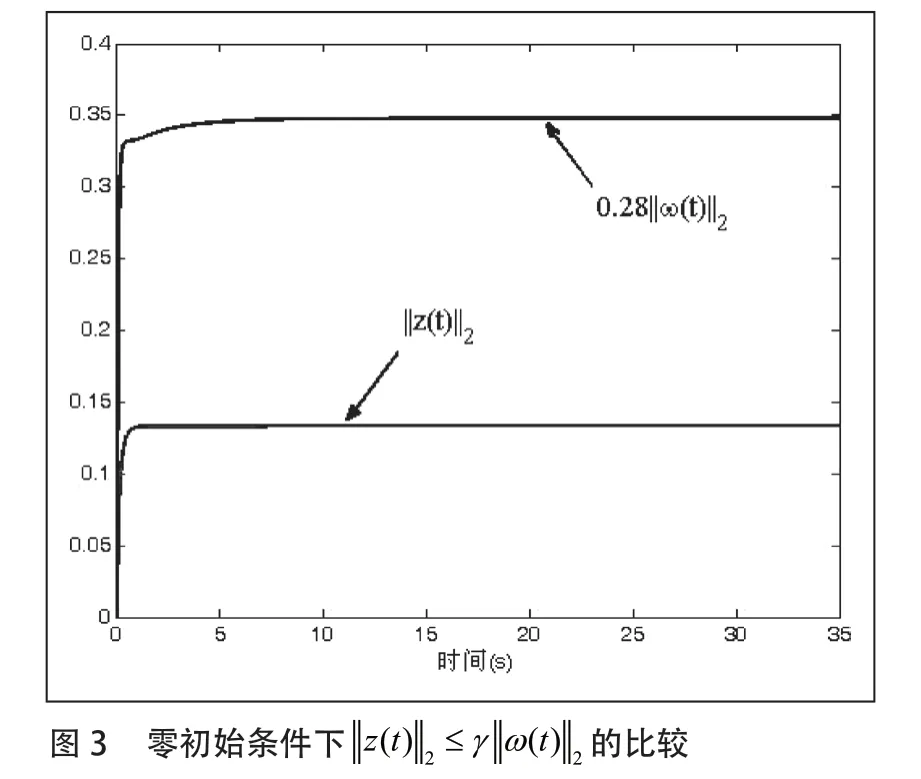
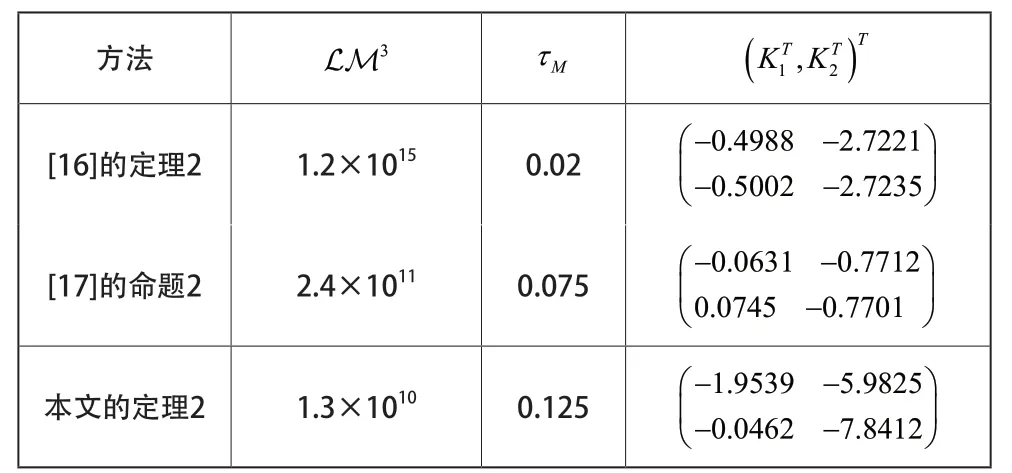
表1 不同方法下的计算复杂度，上界及控制增益的比较

5 结论

本文研究了T-S模糊系统的网络化H∞控制问题。考虑到网 络诱导时延的随机特征，并利用异步归一化隶属度函数的偏差界和归一化隶属度函数的凸性，建模闭环系统成一个带有两个分段区间时变时延和随机参数的异步T-S模糊系统，得到了网络化H∞模糊控制的设计结果。通过仿真例子说明了方法的优势。