基于MEA-BP神经网络的钻井机械钻速预测

张立刚，苗振华，黄小刚，袁胜斌

（1.东北石油大学 石油工程学院，大庆 163318；2.中法渤海地质服务有限公司，天津 300457）

我国油气资源丰富，但随着勘探和开采力度的不断加大，浅部地层和较容易开采的油气资源日益减少，正逐步向深层和非常规方向发展[1-2]。随着开采难度的增加，容易出现钻井周期长、成本高、风险大等问题。因此，如何精准有效地预测出机械钻速对提高钻井效率有着重要意义[3-4]。

机械钻速预测受研究区块地理环境的多重影响，不同学者所建立的机械钻速预测模型存在些许差异[5]，但随着大数据和机器学习等计算机技术的发展，机械钻速预测模型精度在不断提升，为现场高效施工提供了有利的参考依据[6-7]。文献[8]通过可钻性系数、钻压、转速、井深和洗井液冲洗量5 个参数，建立了机械钻速的多元回归预测模型，钻速平均相对误差为7.66%。文献[9]利用BP 神经网络，考虑钻井液密度、钻压、转速、水利参数和钻井液等指标实现井下机械钻速预测，验证了神经网络预测机械钻速的可靠性。文献[10]分别建立了基于决策树、随机森林、全连接神经网络和支持向量机的机械钻速预测模型，结果表明支持向量机的钻速预测模型精度最高。不难看出其他学者在机械钻速预测方法上已经做了许多工作，但是在钻速模型建立过程中多基于单一智能算法实现，且缺乏对训练数据进行充分预处理的过程，造成出现预测误差大、模型稳定性差和容易陷入局部最优等问题。

因此本文考虑一种基于MEA-BP 的混合算法来实现机械钻速预测，利用思维进化算法对传统的BP神经网络进行优化处理，可以有效避免神经网络陷入局部最优。同时对训练数据进行多重预处理操作，降低数据冗余度，进一步提高机械钻速预测精度。

1 算法原理

1.1 BP 神经网络

BP（back propagation）神经网络算法又被称为误差反向传播算法，其具有较高的灵活性，在信号处理、模式识别和智能控制等领域被广泛使用[11]。BP神经网络拓扑结构如图1所示，其中X1～Xn为输入参数值，Y1～Ym为预测结果值，Wij和Wjk为神经网络的权值，网络一般由输入层、隐含层和输出层三部分构成。

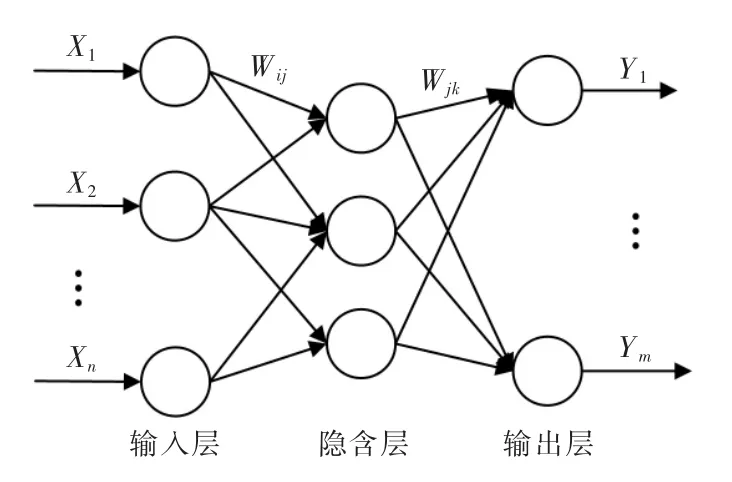
图1 BP 神经网络拓扑结构图Fig.1 BP neural network topology diagram

神经网络中的学习算法由正向传播和反向传播两部分组成，正向传播获得输入数据的真实输出值，而反向传播则根据真实输出值和期望输出值之间的误差来修正连接权值，通过不断修正来减小误差，最终实现更好的目标效果。

1.2 MEA-BP 组合模型

思维进化算法（mind evolutionary algorithm，MEA）受遗传算法（genetic algorithm，GA）的启发进一步演化而来，与遗传算法有着许多相似的特征，保留了遗传算法中的一些概念，其主要由种群、个体、环境和公告板组成[12]。并提出了“趋同”和“异化”的思想，代替了遗传算法中“交叉”与“变异”思想。根据得分函数来判断种群趋同、异化操作是否完成，若完成则输出最优个体，用来训练BP 神经网络模型[13]。

传统BP 神经网络主要依赖误差函数对初始权值和阈值进行调整，容易出现稳定性差、陷入局部最优等问题。大量学者研究表明，通过思维进化算法对BP 神经网络进行优化处理，可以有效避免网络陷入局部最优，提高预测精度[14]。具体的MEA-BP算法流程如图2所示，其实现过程大致如下：

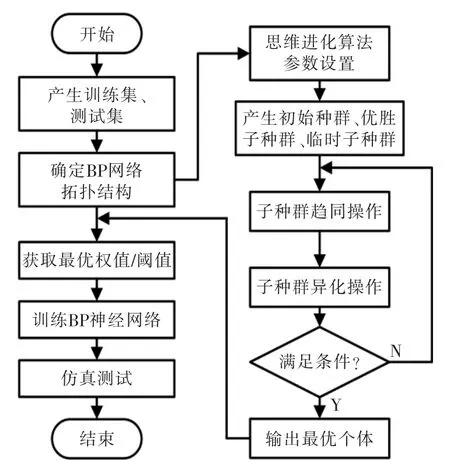
图2 MEA-BP 流程Fig.2 MEA-BP flow chart

（1）数据预处理，确定网络训练数据样本，并设定BP 神经网络的拓扑结构；

（2）思维进化算法参数设定，定义迭代次数、种群大小、优胜子种群和临时子种群大小等参数；

（3）产生初始种群，并计算各种群得分，得分函数为

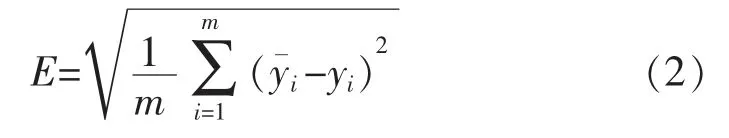
（4）执行趋同和异化操作，通过不断迭代，更新优胜种群和最优得分；

（5）判断是否满足输出条件，若满足则输出最优权值和阈值，否则继续执行上述步骤（4）的操作；

（6）将最优权值和阈值赋给BP 神经网络模型，进行迭代训练，最终输出预测结果。

2 机械钻速预测模型建立

2.1 数据预处理

在实际钻井过程中，机械钻速受到机械参数和钻井液参数的共同影响。本文基于井场实钻数据，综合考虑了机械参数和钻井液参数对钻速的影响。选取深度、钻压、转速、扭矩、泵压、排量、钻头尺寸、钻井液密度8 个参数，为了降低数据的冗余性，通过小波降噪、标准化处理、灰色关联度分析等方法，筛选出和钻速相关性较高的参数，用来预测机械钻速。

2.1.1 小波降噪

钻井数据采集是一个较为复杂的过程，采集到的数据可能会受到工程、环境、人为等多因素的干扰，造成数据出现异常现象。为了消除钻井数据中异常干扰，选择小波阈值降噪方法，该方法通过小波分解、阈值处理和小波重构等流程实现降噪目的[15]。

在小波降噪过程中选择合理的阈值处理方式至关重要，本次选择硬阈值方式，该方式可以较好地保留原信号，且均方误差较小，其公式如下：

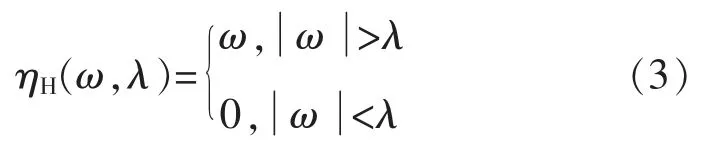
利用硬阈值方法降噪处理后的部分数据如图3所示，通过降噪前后数据对比，可以发现降噪前后数据趋势仍保持一致，并没有改变原始数据特征，并且降噪后的数据相较于原始数据变得更加平滑，消除了一些尖峰状异常数据。

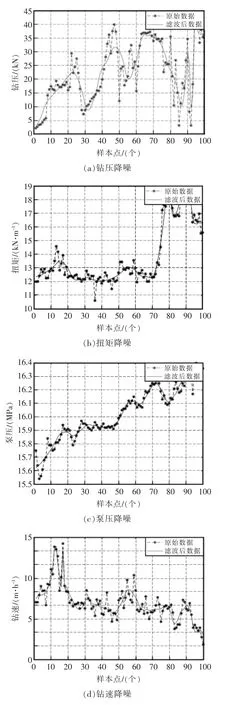
图3 小波降噪前后数据对比图Fig.3 Comparison of data before and after wavelet noise reduction

2.1.2 标准化处理

对小波降噪后的钻井参数进行标准化处理，由于选取的参数在数值分布上和量纲上并不统一，在模型建立过程中难免会受到相应的影响，因此进行标准化处理，消除不同参数之间量纲和量级上的差异。选择min-max 方法来实现，见公式（4），处理后的数据分布在0 和1 之间。

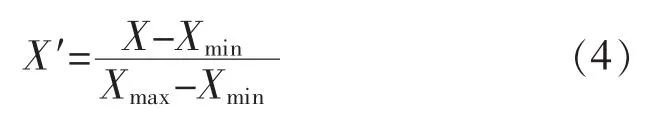
式中：X 为样本值；Xmin为样本最小值；Xmax为样本最大值。

2.1.3 灰色关联度分析

为了提高模型计算速度、降低数据冗余度，通过相关性分析优选出和机械钻速相关性较高的参数。但钻井参数之间关系较复杂，传统的一元多元分析难以刻画各参数之间的关系，因此引入灰色关联度分析方法。通过计算各参数和机械钻速之间的灰色关联度，筛选出灰色关联度较高的参数作为模型输入参数。灰色关联度计算公式如下：

式中：ξi（k）为灰色关联系数；x0（k）为参考序列；xi（k）为比较序列；ρ 为分辨系数，一般取0.5；γi为灰色关联度。

计算出不同钻井参数与钻速的灰色关联度值，将计算结果绘制成柱状图（图4），由图4可知钻压、转速、泵压、排量、密度这5 个参数与钻速的灰色关联度较高，说明这些参数和钻速的相关性更好，因此最终优选出这5 个参数作为钻速预测模型的输入数据，从而实现降低数据冗余的效果。

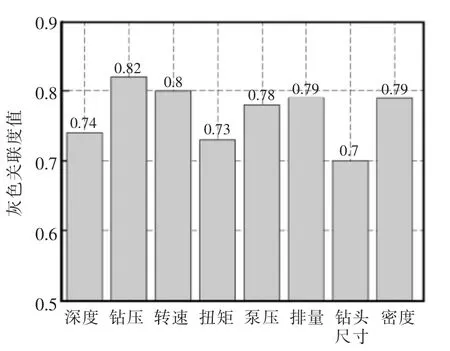
图4 各参数与钻速的灰色关联度值Fig.4 Gray correlation value of each parameter and ROP

2.2 机械钻速预测模型构建

MEA-BP 机械钻速预测模型的建立大致分为4个步骤，钻速预测模型原理框图如图5所示。步骤1为数据预处理，基于井场实测的钻井数据进行小波降噪处理，消除异常尖峰数据，同时对降噪后的数据进行标准化处理，再利用灰色关联度分析方法，把降噪后的数据与机械钻速进行灰色关联度分析，筛选出与机械钻速关联度较高的参数作为BP 神经网络的输入数据；步骤2 和3 为预测模型的建立，在步骤2 中对BP 神经网络和思维进化算法进行初始化处理，思维进化算法进行趋同、异化操作不断更新权值和阈值；步骤3 为神经网络的训练过程，输入优选的5 个参数，经训练后输出预测的机械钻速；步骤4 为模型评价与输出，在训练迭代过程中，若输出结果与目标结果误差较大则调整参数重复执行上述步骤，反之输出预测结果。

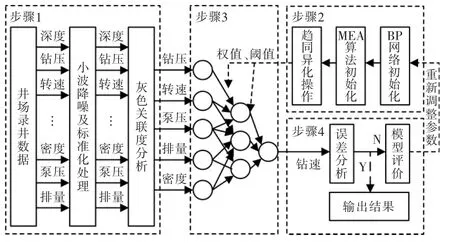
图5 MEA-BP 钻速预测模型原理框图Fig.5 MEA-BP ROP prediction model principle block diagram

3 模型应用与分析

模型数据基于现场某实钻井X1井，该井为直井，实钻井深达到4276 m，且机械钻速波动较大。目的层为前古近系花岗岩和恩平组砂岩，目的层平均机械钻速为9.3 m/h。将上述MEA-BP 模型应用在该井，对机械钻速进行预测，同时与BP 和GA-BP 模型预测结果进行对比分析。

3.1 MEA-BP 模型参数设置

通过数据预处理，确定网络输入为钻压、转速、泵压、排量和密度5 个参数，输出为机械钻速1 个参数，故神经网络输入输出结构为5-1 模式，隐含层单元个数根据经验公式确定，本次模型选择10个，故网络结构为5-10-1 模式。MEA-BP 模型迭代次数设为100，种群大小为200，优胜种群和临时种群个数分别为5。

3.2 结果分析与评价

基于X1井数据，对MEA-BP 进行初始化设定后，MEA 算法执行其特有的趋同和异化操作，通过不断地迭代处理选择合适的权值和阈值，从而提高机械钻速的预测精度。MEA 异化后的趋同过程如图6所示。

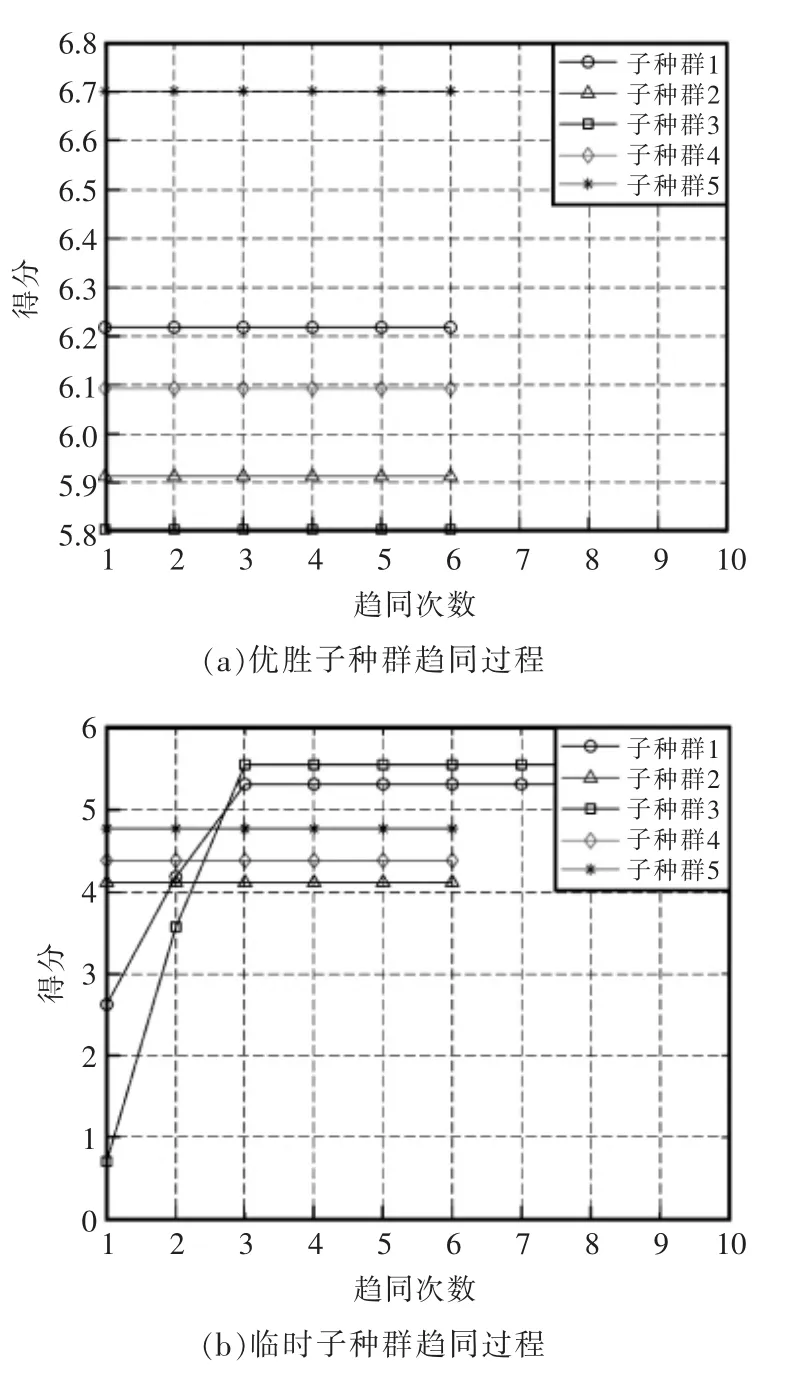
图6 异化后子种群趋同过程Fig.6 Subpopulation convergence process after alienation

根据图6可知，此时图6（a）中5 个子种群的得分不再发生改变，并且得分均高于图6（b）中的临时子种群得分，此时说明趋同和异化操作已全部完成，输出最优权值和阈值。BP 神经网络根据输出的权值和阈值进行模型训练，输出预测的机械钻速结果。

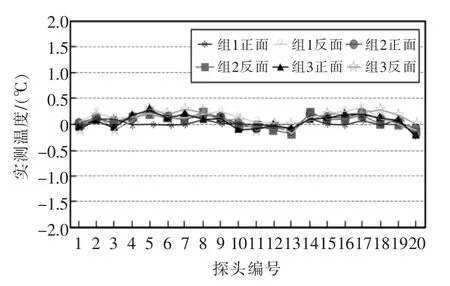
图6 荧光材料浓度对探头一致性的影响Fig.6 Influence of content of phosphor powder to probe consistency

为了验证MEA-BP 模型预测效果，将其预测结果与目前常用的遗传算法优化的BP 神经网络（GABP）和未优化的BP 神经网络的预测结果进行对比，这3 种不同模型的机械钻速预测结果如图7所示。通过该图可知，3 种算法模型都有效地预测出了机械钻速，且与实际机械钻速趋势大致相同，但每个方法预测的结果与实际钻速都存在着些许误差。

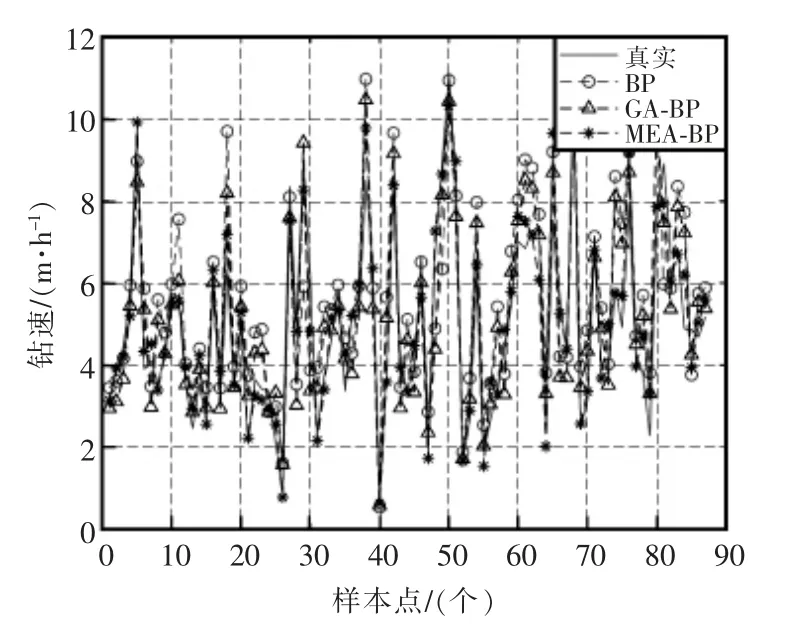
图7 不同模型钻速预测结果Fig.7 ROP prediction results of different models

针对不同模型预测的机械钻速，计算了其与实际机械钻速的误差百分比，并将误差百分比绘制成折线图，如图8所示。同时选取了均方误差（MSE）和决定系数（R2）作为模型的评价指标，具体的评价指标见表1。

图8 不同模型误差对比Fig.8 Error comparison of different models

表1 评价指标Tab.1 Evaluation indicators

由图8中的3 种机械钻速预测模型对比可知，未经优化的BP 神经网络模型预测值与实际值误差波动最大，而GA-BP 模型预测误差相较于BP 神经网络预测结果有一定提升，MEA-BP 模型预测的误差波动最小、效果最好，通过误差比较可知MEA-BP模型预测的机械钻速精度最高。由表1可知，MEABP 模型的均方误差（MSE）为0.060，小于另外2 个模型的均方误差值，并且MEA-BP 模型的决定系数（R2）为0.936，相较于另外2 个模型更接近于1。因此通过思维进化算法优化后的BP 神经网络钻速预测模型，有着更高的精度和更好的拟合度。

4 结语

针对机械钻速预测问题，在传统的BP 神经网络模型上采用思维进化算法进行优化处理，选择更合理的权值和阈值，进一步提高了神经网络的运算速度和泛化能力。

在模型构建过程中，考虑到影响机械钻速的变量多且具有较强的非线性特点。因此对数据进行了预处理，包括小波降噪、标准化处理、灰色关联度分析等操作，预处理后的数据与机械钻速的相关性更高且数据冗余更低，有利于提高模型预测精度。

通过对比BP、GA-BP 和MEA-BP 3 组不同模型预测的结果，发现BP 神经网络预测的结果误差波动较大，预测精度低于优化后的2 组模型，而基于MEA-BP 预测的效果最好。