基于模型预测控制的移动回收站对接控制算法
齐贝贝,宋 敏,王林林,张亚维
(西安航空职业技术学院 航空维修工程学院,西安 710089)
如今人们发现越来越多的资源来源于海洋,因此探索海洋对于获取能源和相关资源意义重大。自主水下机器人AUV 是一种智能化的海洋探测设备,目前已经成为探索海洋资源的重要工具之一。由于AUV 自身条件受限,不能长时间作业,需要及时进行能源补充、数据下载等任务,因此在自主水下机器人的控制过程中,回收控制是重要的关键技术之一[1]。目前在AUV 回收控制的研究中,绝大多数回收站都是静止的,移动回收站的AUV 回收控制研究很少。在整个回收过程中,由于回收站受到海流的影响,AUV 与回收站都处于运动状态。随着AUV 与移动回收站相互接近,两者也会产生相互干扰,AUV 不仅要克服各种复杂约束限制,而且要抵抗外界干扰。所以,移动回收站AUV 回收对接研究具有一定难度[2]。
关于自主水下机器人的水下回收对接问题,国内外的广大学者和研究人员做了大量的研究。为了实现在未知的海流干扰下的回收对接,文献[3]提出了一种基于鲁棒模糊理论的水下航行器对接控制算法,并通过MATLAB 仿真验证了该算法;针对REMUS-100 型AUV,文献[4]设计了一种基于超短基线USBL 定位的回收对接系统,并且成功地完成了对接试验。
关于水下机器人的自主回收对接,国内也有相关的研究成果。文献[5]针对动基座水下航行器回收对接控制,采用了模型预测控制算法,同时满足多种复杂的约束条件,通过仿真验证了算法的有效性。为了满足AUV 水下对接系统的需求,文献[6]建立了AUV 的动力模型,将回收对接控制分为追踪回归和直线对接2 个阶段,通过仿真研究,验证了控制策略的可行性。文献[7]考虑到水下运动母船与AUV 的自主回收控制问题,根据有限时间同步理论,设计了一种能够在有限时间内被运动母艇回收的滑模控制器,并在仿真中验证了该控制器的有效性。
本文在之前研究的基础上,考虑了实际应用场景下,由海流造成的回收站移动的问题,提出了基于MPC 的AUV 移动回收站对接控制算法。针对安装有应答器的移动回收站,采用基于MPC 的对接控制算法对AUV 进行运动控制,其中重点研究了状态约束中的可见性约束和自身约束中的输入约束。通过预测控制器的解算给出最优控制输入,在满足约束条件的同时,实现AUV 的回坞导引控制。最后,在回收站移动的情况下,通过仿真证明了所设计的对接控制算法是有效的。
1 AUV 建模
AUV 的6 自由度空间运动方程是一个较为复杂的非线性系统。在工程实践中,为了研究AUV 的运动规律,常将6 自由度空间运动分解为垂直面运动与水平面运动两部分,同时忽略它们之间的耦合,并假设横滚运动在重力的恢复力矩作用下是稳定的。注意到本文研究的AUV 的回坞过程发生在海面上,因此本文主要研究欠驱动AUV 水平面运动的控制问题,下面给出欠驱动AUV 在水平面内的3 自由度运动模型。
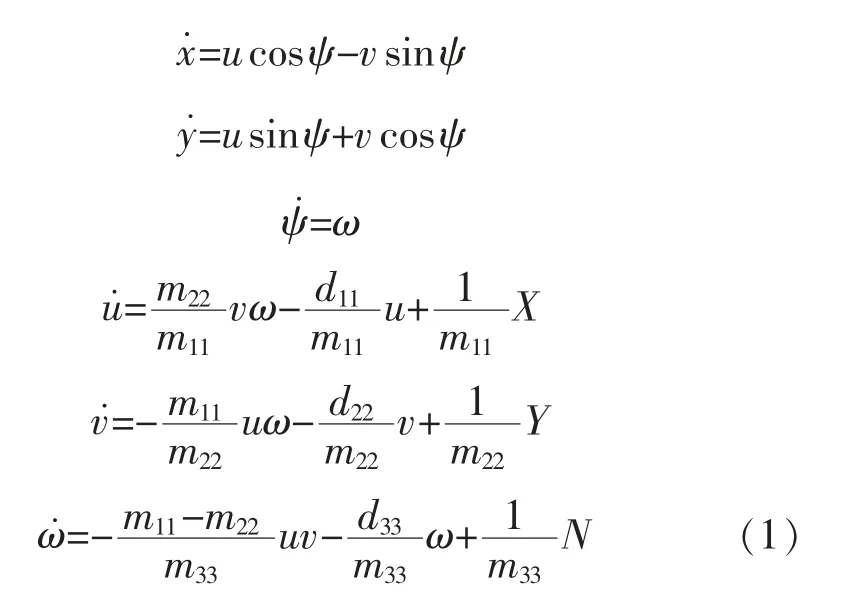
式中:m11,m22和m33为包含附加质量的惯性系数;d11,d22和d33为阻尼系数;X,Y 和N 为控制力和力矩。
2 回收系统
回收对接系统如图1所示,将USBL 的收发器安装在AUV 的头部,2 个应答器安装在回收站的两侧。为了描述AUV 的运动,定义了对接坐标系和体坐标系。回收站上的2 个应答器的中点作为对接坐标系的原点,记为原点O,沿着x 轴的方向为回坞的方向,y 轴与x 轴垂直;AUV 的浮心作为体坐标系的原点,记为原点OB,AUV 的纵轴为xB轴,并指向运动的前方。
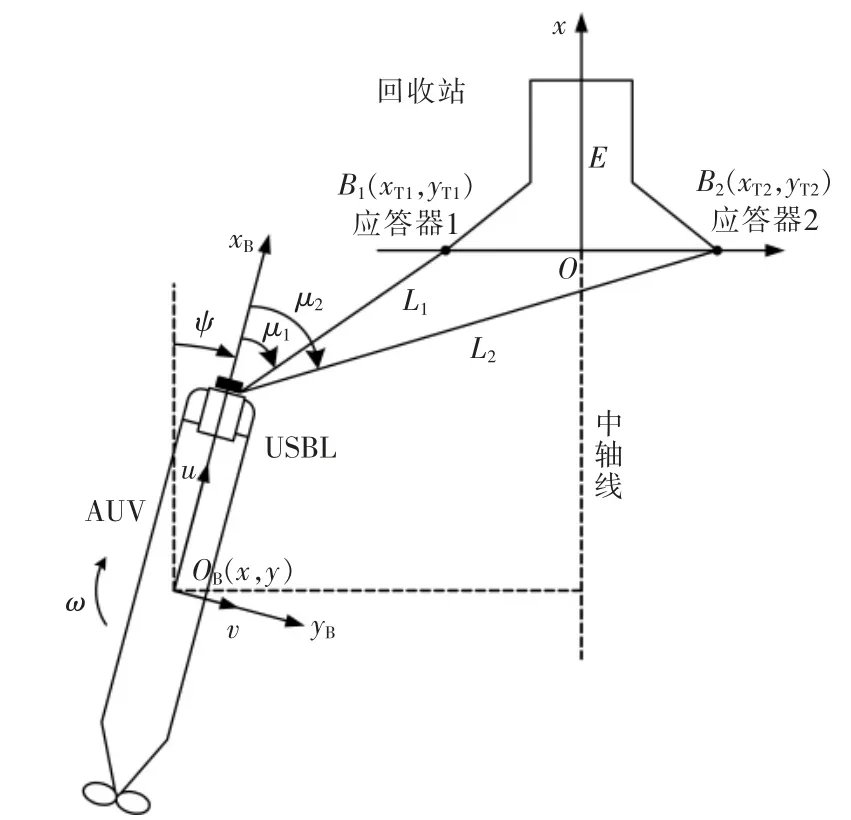
图1 AUV 回收对接系统图Fig.1 Diagram of AUV docking system
3 回坞导引模型预测控制设计
模型预测控制算法在设计时就有约束项,因此在处理带有约束的控制问题时,较其他算法具有优越性。本文提出的基于模型预测控制的AUV 回收控制算法中,重点研究了约束优化问题,模型预测控制器解算出的最优控制输入在满足约束的同时,完成AUV 在水平面内的回收。
在欠驱动自主水下机器人AUV 的水平面运动方程中,x= [x yψ]T是AUV 的广义坐标矢量,v=N为系统的输入量。
在欠驱动AUV 的水平面回收控制问题中,利用模型预测控制算法设计回收对接预测控制器。在时间间隔[t,t+TP]内,计算与系统状态x(t)有关的代价函数。然后最小化代价函数从而得到最优的控制输入,并且将最优的控制输入作用于在比预测时域TP短的控制时域Tc上。
本文的代价函数选择了最简单的二次型,处理系统约束优化问题的代价函数为[9]
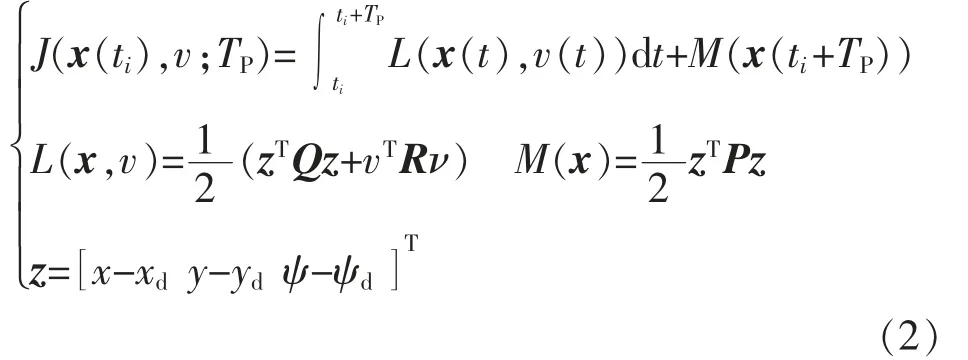
式中:L(x,v)是代价函数;M(x)是终端代价函数;Q和R 分别为状态代价权重矩阵和输入代价权重矩阵;P 为终端状态代价权重矩阵;xd= [xdydψd]T为AUV 期望的广义坐标矢量。
王霞在知道到这件事情后,这次来皮山结亲,专门看望了这个特殊家庭,并为孩子带来一些学习用品和冬日御寒的衣服,为老人带来一些礼品。王霞表示,她会一直关心这两个孩子,一起面对困难,让孩子健康成长……
然后求解系统约束优化问题:

同时满足下列2 个约束条件:

式中:v∈K 为系统的输入约束;x(ti)∈Ω 为系统的状态约束。本文在下一节中详细给出这2 种约束的处理。
在时刻ti,模型预测控制MPC 算法包括以下几个步骤[10],如图2所示。
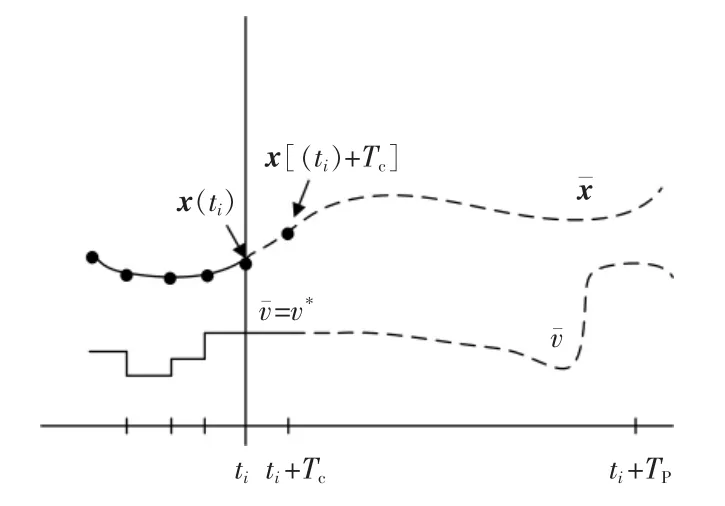
图2 MPC 算法示意图Fig.2 Schematic diagram of MPC algorithm
(1)测量ti时刻系统的坐标x(ti)。
(2)通过在线求解系统约束优化问题(3)从而得到开环的优化控制输入[ti,ti+TP]。
(3)把控制时域Tc内的第一个输入v*,即[ti,ti+Tc]中的第一个控制输入施加给系统。
(4)在下一个采样时间ti=ti+Tc,重复上述优化问题从而形成模型预测控制律。
4 约束系统
在移动回收站AUV 对接回收过程中,存在着多种复杂的约束。本文主要研究的约束问题是状态约束中的可见性约束和自身约束中的输入约束。
4.1 可见性约束
状态约束中的可见性约束指的是USBL 对应答器可见性的约束[11],即在AUV 回坞过程中,回收站要始终处在USBL 的工作扇面之内。系统的可见性约束如图3所示,USBL 收发器的可视角为α,可视角是关于xB轴对称的,回收站上应答器的位置范围为[-yT,yT],USBL 的工作区域为[ f2,f1]。回收站上应答器的位置在USBL 的工作区域内,即[-yT,yT]⊆[f2,f1]。将可视角α 平移到AUV 的浮心,与回收坐标系的y 轴交于A′和B′两点,USBL可视范围变为[f2′,f1′]。由直角三角形A′O′OB和B′O′OB得:
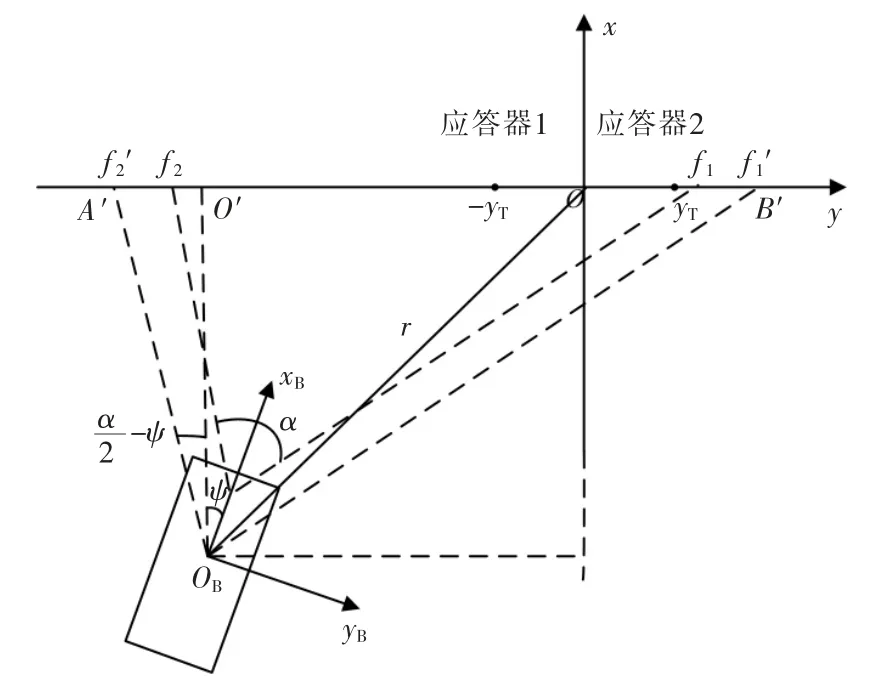
图3 水平面内AUV 回坞可见性约束示意图Fig.3 Schematic diagram of docking visibility constraints of AUV in horizontal plane
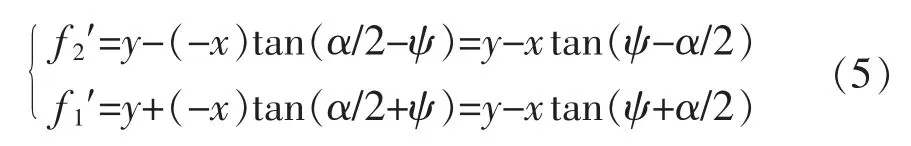
显然,f2′≤f2,f1′≥f1。因此,f2′≤-yT,f1′≥yT,即:

综上,可将可见性约束写为如下3 个不等式:
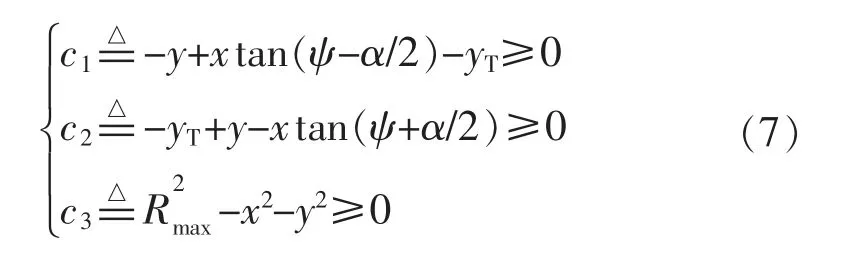
4.2 输入约束
由于自主水下机器人AUV 本身硬件性能的原因,所以存在自身约束。本文中主要研究的自身约束是输入力矩约束,可以表示为

因此,求解约束优化问题:

满足约束条件:
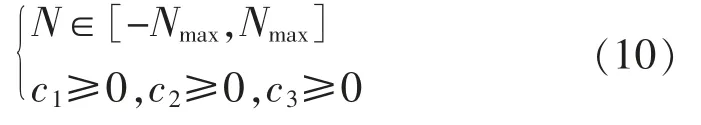
目标函数为

式中:L(x,v),M(x)和z 的定义与式(2)中的定义是相同的。
5 仿真验证
为了验证提出的基于模型预测控制的移动回收站对接控制算法,本文采用REMUS AUV 模型参数进行仿真研究。仿真中,设AUV 起始点坐标为(-8,-10),初始航向角为45°,前向速度为1 m/s,回收站的初始位置为(-1,0),受到海流的干扰,以0.05 m/s 速度沿y 轴正向运动,期望的入坞方向为0°。正定矩阵Q∈R3×3,Q=diag([1 300 500]),R=1。控制输入N∈[-100,100],可视角α=120°,即可视范围为[-60,60]。在回坞过程中考虑了状态约束中的可见性约束和自身约束中的输入约束,求解代价函数得到最优的控制输入。通过仿真得到AUV 预测控制回坞轨迹如图4所示,从图中可以看出在模型预测控制下,AUV 能够以较光滑的轨迹、较短的时间航行到移动回收站。AUV 回收对接中航向角变化如图5所示。AUV 回收对接中控制输入变化如图6所示,由图可见,控制输入不超过100 N·m 满足输入约束。仿真结果验证了算法的有效性。

图4 AUV 模型预测控制回坞轨迹Fig.4 AUV docking trajectory with MPC
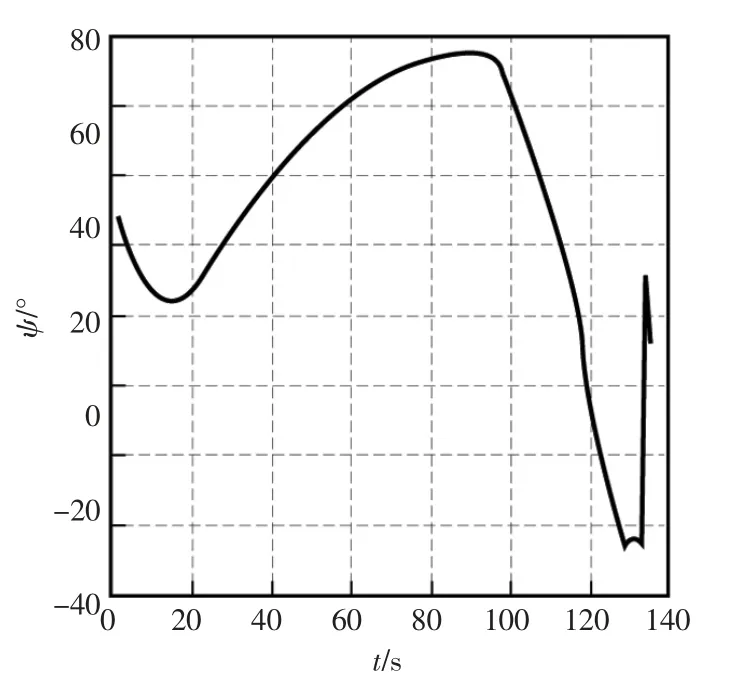
图5 AUV 模型预测控制回坞航向角变化图Fig.5 Yaw angle of AUV docking with MPC
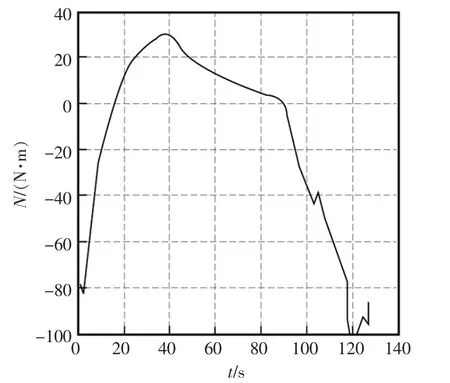
图6 AUV 预测控制回坞控制输入变化图Fig.6 Control input of AUV docking with MPC
6 结语
本文针对自主水下机器人AUV 回收对接控制问题,提出基于模型预测控制的移动回收站对接控制算法。回收站在海流的作用下发生移动,采用模型预测控制MPC 算法设计回收对接预测控制器,来完成回收对接。在MPC 算法中,重点研究了状态约束中的可见性约束和自身约束中的输入约束。最后,通过采用REMUS AUV 的模型参数进行仿真,仿真结果证明了自主水下机器人的移动回收站对接控制算法是有效的。

