基于LMS的环型TMR阵列传感器滤波算法设计
陈泽纯,石洪,赵聪,陈月
(1.国网湖北省电力有限公司营销服务中心(计量中心),武汉 430000; 2. 黑龙江省电工仪器仪表工程技术研究中心有限公司,哈尔滨 150000)
0 引 言
随着光伏、风电、电动汽车等新能源系统的发展,采用非接触式隔离测量技术的电流互感器在电力工业的需求日益增加[1-3]。然而,传统的霍尔电流传感器存在灵敏度低、功耗高、线性度差等缺陷,无法满足适应复杂的电磁环境。为了实现高精度、低成本的电流测量,迫切需求新型材料的传感器技术[4-6]。
根据传感器薄膜材料的不同,磁阻传感器可分为各向异性磁阻(AMR)[7-8]、巨磁电阻(GMR)[9-11]、隧道磁阻(TMR)[12-14]传感器等。其中,AMR的灵敏度优于霍尔传感器,但其线性范围较窄,需要通过置位/复位线圈对其进行置位/复位,使得AMR传感器制造过程复杂;GMR传感器的薄膜中间层采用金属材料,容易受到环境温度等周围因素的影响,不适用于高频信号采集;相比较于霍尔、AMR、GMR传感器,TMR传感器的中间层采用绝缘材料,能够更好地适应温度变化,并且具有灵敏度高、低功耗、高线性度和较宽范围频率响应等优点。
为了进一步提升磁阻传感器的测量效果,通常将传感器设计为环型磁阵列,即将多个磁阻传感器均匀地分布在导体周围测量磁场强度[15-17]。这种结构能够降低传感器的体积和质量,提升磁阻的抗饱和能力。然而实际工程中,由于铁芯不能完全屏蔽外界磁场,位于环型传感器外部的磁场源会在测量目标电流时产生干扰,降低测量精度。文献[18]采用Kalman滤波器,对传感器测量的磁场强度进行滤波处理,从而获得较为精准的导体电流,但该方法只验证了小电流工况,不能有效应用于大电流测量场景。文献[19]提出一种求和算法,将各传感器的输出求和,然后通过计算平均值的方式估算待测导体周围的磁场强度,但测量的精度有待进一步提高。
针对上述问题,本文分析了环型TMR阵列传感器的测量原理,并提出了一种基于最小均方根(Least-Mean-Squares,LMS)算法的磁阵列测量滤波算法,数值仿真和实验结果表明该方法的正确性及有效性。
1 环型TMR阵列传感器测量原理
环型TMR阵列传感器是由多个TMR传感器元件均匀分布在导体周围的圆形PCB组成[20-21],如图1所示。以N个TMR传感器形成的半径为r的传感器为例,载流导体穿过环形阵列。假设需要被测的载流导体穿过环型阵列的中心点,并且与磁阵列所在的空间平面垂直,则根据毕奥萨伐尔定律,待测导体沿着单个TMR传感器元件与中心方向的灵敏点的磁感应强度为:
式中μ0为自由空间的磁导率;I为待测导体的电流。
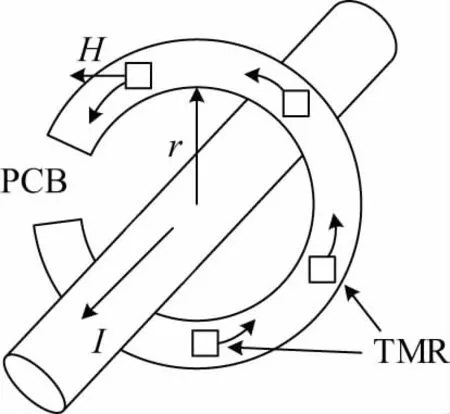
图1 TMR电流传感器开环结构示意图
因此,包含N个TMR元件的环型磁阵列传感器测得的磁感应强度为:
式中 定义磁阵列上的TMR传感器个数为N;每个传感器元件对应的灵敏度单位方向向量为s;下标i表示为第i个TMR传感器。如果载流导体没有穿过环形阵列的中心或者没有垂直于阵列平面,则ri的取值将发生变化。因此根据式(2),载流导体电流被测量出的电流大小为:
2 磁阵列滤波算法设计
2.1 LMS算法的基本原理
图2为LMS滤波器[22]的基本结构,xk和wk(k=1,2,...,n)为样本的输入信号和权重系数,y为输出信号,d为期望的响应即参考值,e为输出信号和参考值的误差。

图2 LMS滤波器基本结构
当前滤波器的输出信号y可表示为:
则样本的误差e表示为:
e=d-y=d-wTx
(5)
一般取估计误差e的均方值J作为评价线性滤波器的性能指标,即:
为了便于实际计算过程,将单次数据的平方误差e2代替均方误差J。则梯度向量的估值可表示为:
考虑图6所示的线性滤波器,利用来搜索权向量wk的维纳解wopt的最速下降法,成为自适应LMS算法,即:
式中μ是自适应增益常数。
因此自适应LMS算法的实现步骤如下:
(1)初始化:w(0) = 0,,选取自适应常数μ,并且有0<μ<1;
(2)迭代计算:根据式(4)~式(8),有:
(3)收敛条件:
式中a是用于判断收敛的常数,一般取0.05。
2.2 基于LMS算法的磁场滤波方法
磁传感器阵列在测量环型阵列内部磁场时,容易受到外界磁场的干扰,影响测量精度。文中根据最小均方根(Least-Mean-Squares,LMS)算法,提出一种降低磁场干扰的磁阵列自适应测量的方法,当磁感应强度作为输入时,LMS算法的表达式为:
其中,为滤波器处理后的磁感应强度;w1(t),w2(t),…wM(t)为在t时刻的权重系数,M表示滤波器抽头数即滤波器的阶数;μ为收敛因子,为恒定值,其小于输入信号相关矩阵的最大特征值倒数;Btar(t)为载流导体产生的磁感应强度的实际值,Bi(t)为各传感器检测的磁感应强度。
式(11)得到的基于LMS算法的磁场估算流程图如图3所示。其中,B(t)=[B1(t),B2(t),…,BM(t)],W(t)=[w1(t),w2(t),…,wM(t)]。磁场的输入形式可以为以下两种情况:(1)环型磁阵列中M个磁传感器在同一时刻输出,即为M个数值;(2)环型磁阵列中M个磁传感器在同一时间段输出,即为M个集合。
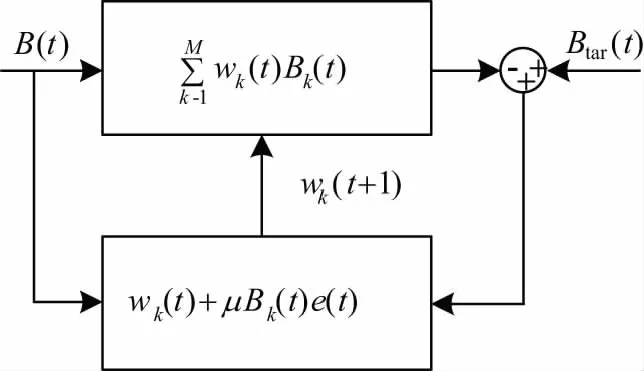
图3 基于LMS算法的磁场估算流程图
2.3 磁阵列模型分析
为了进一步分析磁阵列的工作性能,建立磁阵列模型,即采用三个磁传感器元件均匀分布于载流导体的周围,并将某一段时间内磁传感器检测的磁感应强度作为LMS滤波器的输入,磁阵列模型如图4所示。根据毕奥-萨法尔定律,磁传感器Si(i=1,2,3)检测到载流导体的磁感应强度为:
其中:

图4 基于LMS算法的磁阵列模型
图4中,载流导体1中的电流I1(t)为磁阵列要测得的目标电流,载流导体2的电流I2(t)为对磁阵列产生干扰的电流。两个导体间的距离为D,Bφ和Br为对磁传感器产生干扰的两个分量。其中Bφ是平行于磁传感器的分量,Br为载流导体1沿着磁传感器延伸方向的分。将TMR传感器在某段时间内的输出作为输入,则有:
式中B1(t)、B2(t)、B3(t)为三个磁传感器在时刻t时刻测得的磁感应强度;为经LMS滤波器滤波后的磁感应强度。根据式(2),最后测得的磁感应强度为:
2.4 三相交流系统测量方法
上述方法仅分析了干扰电流为一平行电流的情况,因此在测量三相交流系统某相电流时,需要对算法进行改进。三相交流系统的磁阵列模型如图5所示,其中,I1为待测相导体的电流,I2和I3为其余两相的电流,即干扰电流,每个磁阵列包含4各TMR传感器。

图5 三相交流系统的磁阵列模型
根据毕奥-萨法尔定律,四个TMR传感器测得的磁感应强度为:
将式(16)的结果代入式(11)进行LMS滤波处理,最后根据式(2)计算传感器的测量结果。
3 数值分析
为了进一步分析基于LMS滤波算法的磁场测量的正确性和有效性,本文对载流导体间的距离D和载流导体与磁传感器的距离R进行了数值仿真分析。
假设载流导体1的电流I1(t)和干扰磁场的导体2的电流I2(t)为正弦信号,频率50 Hz,电流的幅值分别为500 A,1 000 A和1 500 A。
(1)工况1:令载流导体间的距离D为0.12m,通过改变载流导体与磁传感器的距离R的值,改变二者的值。当Φ1为0,则磁感应强度通过公式计算,得到估算磁场与目标磁场的均方根误差(Root Mean Square Error,RMSE),如图6所示,当D/R为2时,RMSE最小。
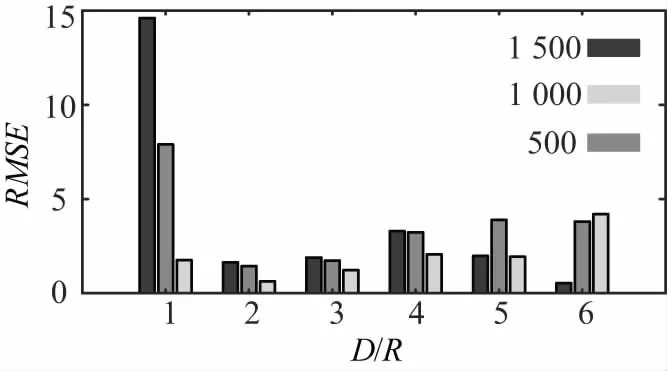
图6 均方根误差随D/R的变化
(2)工况2:令载流导体和干扰磁场的导体的电流均为500 A,改变载流导体与磁传感器的距离R的值。最终结果如图7所示。可以看出,R的值呈现非线性变化,当保持一定距离时,能有效降低RMSE。

图7 均方根误差随R的变化
(3)工况3:根据工况1、工况2的仿真结果,设定载流导体与磁传感器的距离R为0.06 m,载流导体间的距离D为0.12 m,Φ1为0。使干扰磁场的导体2的电流I2(t)从I1-250 A到I1+250 A变化,数值仿真结果如表1所示。

其中,Bc为经过滤波器得到的估算磁感应强度,Bo为载流导体产生的磁感应强度。可以看出,随着被测导体电流的增加,测量磁场的误差将放大。当I1=1 500sin(100πt)A,I2=1 550sin(100πt)A时,RMSE最大,为89.44%,此时滤波后磁感应强度波形与目标电流产生的磁场波形如图8所示。
下面对三相交流系统下传感器性能进行仿真分析,分别令磁传感器的个数为2个~4个,排列方式根据图8进行排列。其中,TMR传感器与载流导体的距离R的值为0.15 m,载流导体间的距离D为0.3 m。假设载流导体1的电流I1(t)为δsin(100πt),干扰磁场的导体2、导体3的电流I2(t)和I3(t)分别为δsin(100πt-2π/3)和δsin(100πt+2π/3),δ的变化范围从100 A~600 A。仿真结果如图9所示。

图8 滤波后磁场、目标磁场及误差曲线
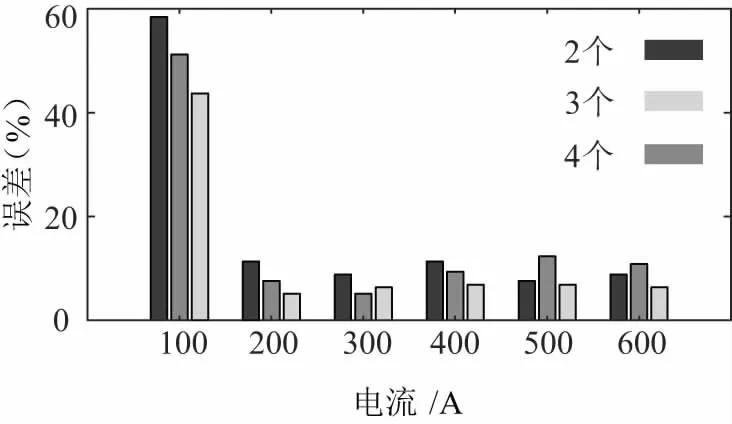
图9 不同传感器个数对测量精度的影响
4 实验结果分析
为验证文中算法的有效性,搭建实验测量系统,如图10所示,其中,环型TMR磁阵列传感器样机的圆周的半径为15.6 mm,4个TMR传感器元件选用TMR2301,该元件的温度稳定性良好,磁场饱和度±500 Oe,灵敏度为1 mV/Oe,带宽200 kHz;电流测量采用CA-PAC12型号电流钳,并通过示波器读取载流导体的电流数据;传感器测量数据通过数据采集器读取并由USB上传至上位机,利用MATLAB软件进行滤波处理。
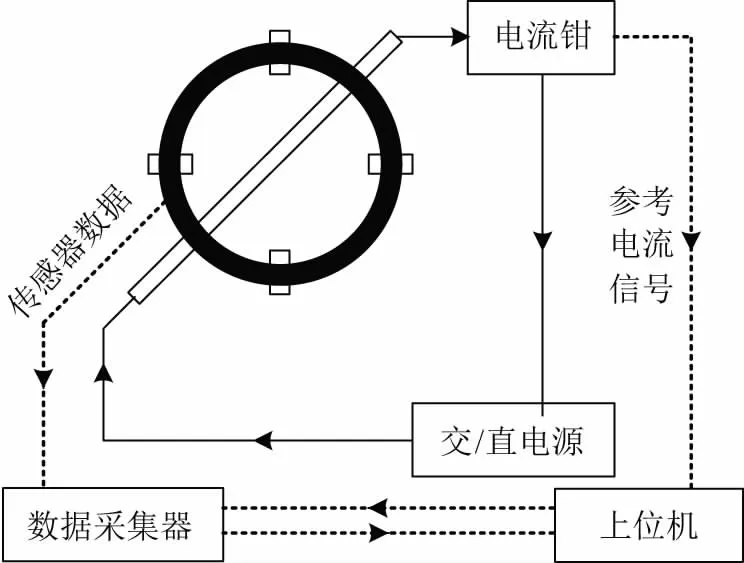
图10 实验测试系统
在接下来的实验中,分别设置直流电流为100 A,交流电流的有效值为100 A,电流钳测量的电流如图11和图12所示,TMR传感器测量的电流如图13和14所示。相对于电流钳测量的实际电流,TMR传感器样机的测试精度更高,其中直流电流和交流电流的平均误差分别为0.41%和1.21%。

图11 电流钳测量的直流电流
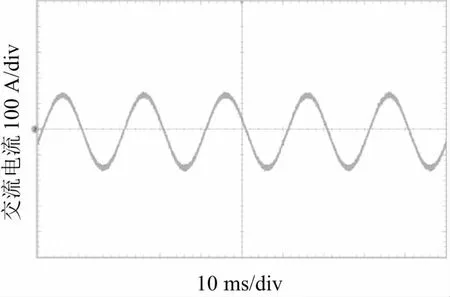
图12 电流钳测量的交流电流

图13 TMR传感器测量的直流电流

图14 TMR传感器测量的交流电流
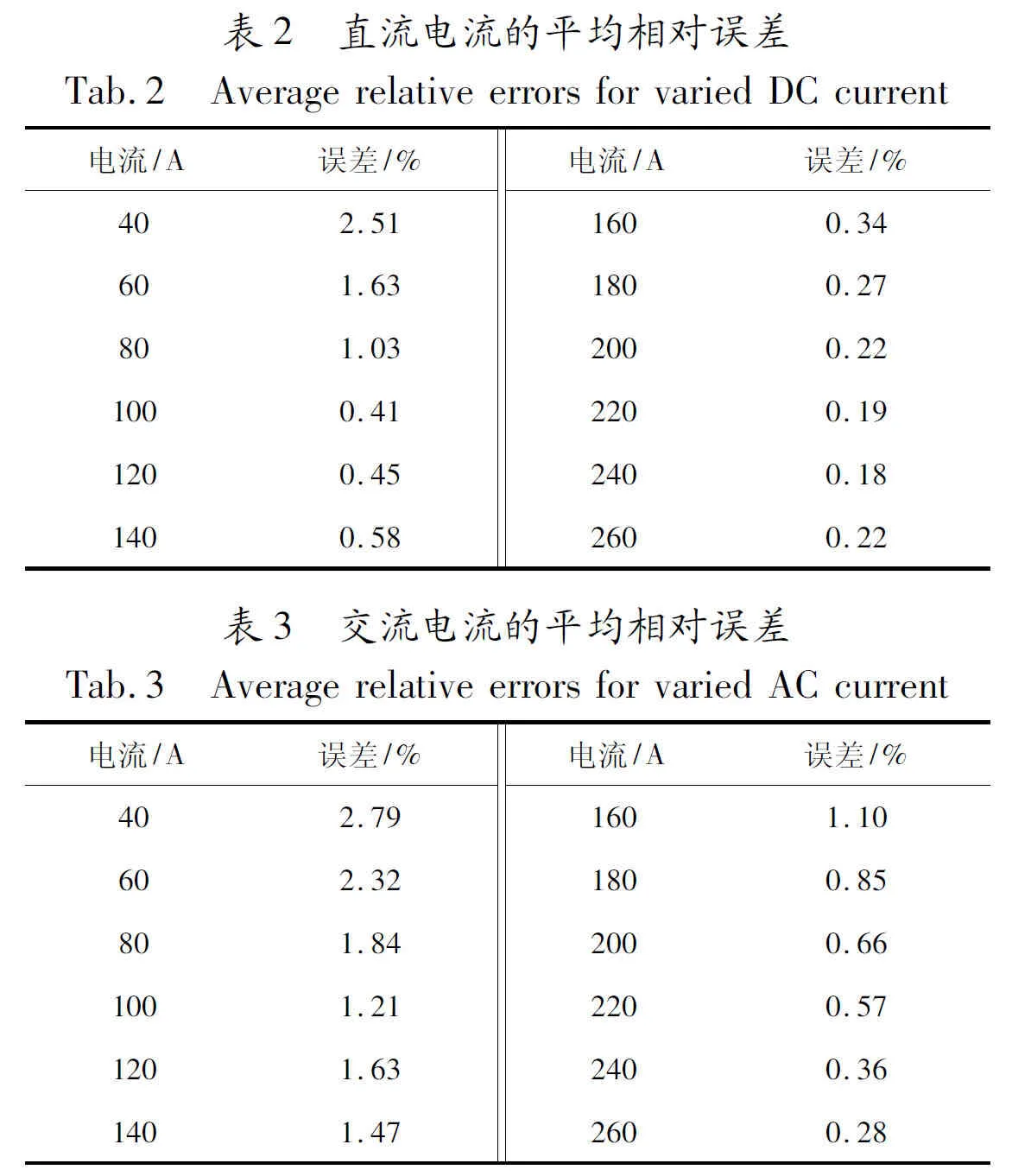
此外,对测量系统的动态范围进行了实验分析。分别进行了从40 A~260 A的直流和交流实验。表2和表3显示了电流测量时的平均误差。由于TMR传感器和采集芯片存在固有误差,使得平均相对误差随着电流的增大而减小。
进一步分析干扰环境下,环型TMR传感器的测量精度,令干扰电流导体平行于待测导体,则考虑干扰电流的实验测试系统如图15所示。此时,被测电流与干扰电流的值相同。

图15 考虑干扰电流的实验测试系统
测量系统的动态范围为40 A~260 A,直流和交流测量结果如表4和表5所示,电流钳交流测量结果如表6所示,可见环型TMR传感器的测量精度满足大电流测量需求,并且有较好的抗干扰能力。

5 结束语
文章提出了一种环型TMR阵列传感器自适应滤波算法,采用LMS算法设计自适应滤波器,降低传感器输出信号与期望响应的误差。数值和实验结果表明,所提出的滤波算法能够有效屏蔽外界磁场,降低其对环型阵列内部磁场的干扰,提升测量精度,相对于当前的钳形电流传感器测量装置具有更小的平均相对误差,符合实际工程需求。

