问题解决模式下“空间三角”单元教学研究

沈 良

(萧山区第五高级中学，浙江 杭州 311202)

在以核心素养培养为目标的新课程背景下，单元教学显得越来越重要，它有利于将碎片化知识转化为系统性知识，有利于提升学生的学习能力，从学习专家结论转变为能像专家一样思考问题.而如何更好地理解教材、挖掘教材，更好地开展单元教学值得我们深入研究.本文以喻平教授关于“以问题解决过程线索为主题的单元教学模式”的理论为指导，探索“空间三角”(本文指“异面直线所成的角”“直线与平面所成的角”和“二面角的平面角”)的单元教学研究，谈谈问题解决模式下数学单元教学的落实与推进.

1 内容重构的背景

2019年人教版高中《数学(必修2)》第8.6节“空间直线、平面的垂直”中，包含“直线与直线垂直”“直线与平面垂直”“平面与平面垂直”这3个部分内容，其中又涵盖了“异面直线所成的角”“直线与平面所成的角”“二面角”的学习.“空间直线、平面垂直”与“空间三角”的定义交织在一起，通过异面直线所成角为直角定义了两条异面直线垂直；通过直线与平面垂直找到斜线在平面内的射影，从而定义了直线与平面所成的角；通过二面角的直二面角定义了面面垂直.以垂直为主线展开研究，有两个方面重要意义：一方面，继续加强从“一般观念”上的引导，让学生明确“什么是空间直线、平面的垂直”以及“当空间直线、平面垂直时，其要素中有什么确定的不变关系”；另一方面，充分类比空间直线、平面平行关系的研究方式，引导学生研究空间直线、平面之间的垂直关系.

开展以空间三角为主线的单元教学实践需考虑以下4个方面：

1)问题的普遍性.空间三角作为刻画直线、平面之间相对倾斜程度的几何量，在生产、生活实际中具有普遍性，是我们研究直线、平面位置关系经常需要面临的度量问题.而垂直作为一种特殊的位置关系固然值得我们重点研究，但特殊寓于一般中，设计从一般到特殊的学习路径同样值得我们研究.

2)思想的一致性.教材中，空间三角定义给出平面化的方法，渗透了降维思想.两条异面直线所成的角通过平移用相交直线所成角刻画，直线与平面所成角用直线和它在平面上的射影所成角定义，而二面角的平面角则用棱上一点在两半平面内分别作棱垂线的夹角定义.概念建构思想的一致性，有利于我们开展空间三角的类比学习.

3)知识的发展性.“点动成线、线动成面、面动成体”，从降维思想出发，引申出这样的思考：直线与平面所成角可否用该直线与平面内直线所成角刻画，平面与平面所成角能否用直线与平面所成角去度量刻画.也就是从事物的发展性考虑，寻找“线线角、线面角、二面角”建构过程中的内在联系性.

4)内容的系统性.当有了3个空间角的概念后，在一般化的问题中，特别是在变化过程中，我们需要更进一步研究这3个角的联系，培养学生从孤立到联系看问题的习惯.同时，数学是人类对事物抽象结构与模式进行严格描述的一种通用手段，能否抽象出一个几何模型刻画空间三角的大小关系，这是培养学生模型意识的重要方面.

2 内容重构的路径

基于上述思考，笔者尝试以“空间三角”为主线、“空间直线、平面垂直”为辅线进行单元教学设计.又因空间三角是我们现实中经常会面临的度量问题，这类问题具有极强的现实意义，故笔者开展以“问题解决过程为线索”的主题单元设计.以问题解决过程线索为主题组织单元，是指在解决问题的过程中可能会出现许多新问题，然后以这些新问题串为主线展开研究进而产生新知识学习的单元教学设计[1].

本单元总共包含5课时内容设计，主要为“异面直线所成的角”(1课时)、“直线与平面所成的角”(1课时)、“二面角”(2课时)以及“空间三角联系”(1课时).每课时主要包含“问题聚焦、概念生成、模型建构、联结应用”这4个段落推进.基于问题解决感知各空间角的度量，通过操作确认感受直觉合理性，借助几何模型开展推理论证感受数学严谨性，最后进行计算应用.

1)问题聚焦.在以问题解决过程为线索设计空间三角教学中，一个好的问题包含3个方面重要特征：①情境性，空间角的度量源于生活，在教学中应尽可能选择一些生动的情境，激发学生学习的积极性，也能使学生了解数学学习的现实意义；②建构性：问题的选择不仅要实现解决问题本身，也要能较好地实现知识建构，特别是在以空间三角为研究对象的过程中，需要融入“空间直线、平面垂直”的学习，故选择的情境问题要利于知识的建构与发展；③度量性：空间三角本身就是为度量而用，因此教学中选择的问题尽量以具体运算为对象，让学生在计算过程中，感知角的定义与大小，由感性认识发展到理性认识.

2)概念生成.以问题解决过程作为单元教学的主题，一定程度上颠覆了教材中以知识逻辑结构为顺序的过程，它从解决问题入手，分析可能产生的概念和命题，厘清知识产生的缘由，还原知识的形成过程[1].在空间角问题解决过程中，逐步完善空间角定义，逐步提出“空间直线”“平面垂直”的定义，进而得出空间直线、平面垂直相关的判定定理和性质定理等.

3)模型建构.明确概念的内涵和外延之后，需要思考概念所具有的性质，特别是能否找到探索概念性质的一般规律或模型，从而对概念进行结构化处理.立体几何中相关性质的探索必然是借助特殊几何体模型实现的.在空间角的学习中，重要的是思考线面角、二面角的性质具有怎样的性质，可以发现最小角性质定理和最大角性质定理，且这两个性质定理可在几何体“鳖臑”中有较好的呈现.

4)联结应用.“联结应用”指的是对概念的进一步理解和应用.在建构完知识体系后，接下去是呈现知识学习的意义，体现数学的应用价值，也是对教学中一开始提出问题和解决问题的呼应，空间角学习的意义自然是刻画空间直线、平面的相对倾斜程度.

3 内容重构的目标

以“空间三角”为主线的单元学习，教学目标包含以下5个方面：

1)理解空间三角所表达的物理意义——刻画相对倾斜程度，对数学中的“定量刻画”有一定认知;

2)理解空间三角的定义，能运用定义求解简单的空间角大小;

3)运用联系的观点看待空间三角关系，构建几何模型证明三者的不等关系，得出空间角的两个性质定理，并能在简单问题中判断空间角的大小;

4)在问题解决过程中，渗透空间直线、平面的垂直关系的概念，由平行类比学习空间直线、平面的判定定理和性质定理等;

5)通过空间三角的学习，体会转化思想在空间几何度量中的作用(空间问题平面化)，并对数学概念的建构有一定认知，进一步培养学生数学抽象、直观想象和逻辑推理等素养.

4 空间三角单元教学实践

以“问题解决过程为线索”的主题单元设计，往往会选取一些比较经典的实际问题，在没有明确严格定义一些概念的情况下，通过直觉感知的方式尝试解决问题.这是一个从问题提出、问题解决、再逐步修正完善概念、最后利用概念度量相关问题的过程.这个过程与教材中以逻辑严密的方式呈现内容不同，更加注重学生问题解决的直觉性，使学生能更好地明白概念学习的必要性，更有利于学生从学习专家结论到能像专家一样思考的转变.

下面笔者结合教学实践，从“第2课时：直线与平面所成的角”“第3课时：二面角(1)”的教学过程，谈问题解决模式下的单元教学实践.

4.1 “第2课时：直线与平面所成的角”的教学过程

4.1.1 问题聚焦

例1如图1，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若AB=15 m，AC=25 m，∠BCM=30°，试求tanθ的最大值.

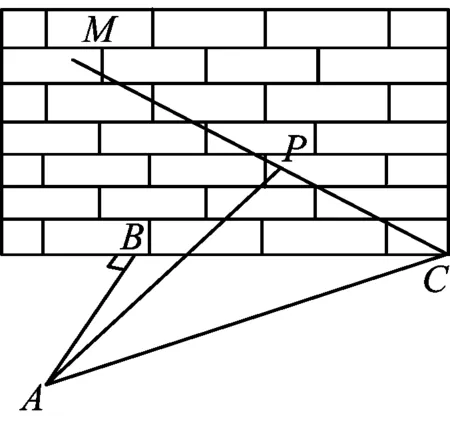
图1

(2014年浙江省数学高考理科试题第17题)

教学中抛出问题，先让学生独立思考，然后小组讨论，最后师生共研.教师主要引导学生思考两个方面核心内容：

1)如何表示这个仰角；

2)如何刻画仰角的正切值.

在教学中，学生提出过点P作BC的垂线PD，联结AD，则∠PAD为仰角θ.设PD=x，得

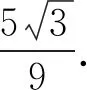
教师肯定了学生们的智慧，在还没有完全明确线面角概念学习的情况下，凭数学直觉找到了这个角，既体现了数学的自然性，也体现了学生直觉的正确性.教师进一步梳理：所谓仰角指的是直线AP相对于水平面ABC所成的角，这个角可称为直线与平面所成的角.

4.1.2 概念生成

那么一般地，如何定义直线与平面所成的角？师生将目光共同聚焦于线面角的定义探索.教师给出一个平面α和它的一条斜线l(如图2)，让学生尝试定义线面角.

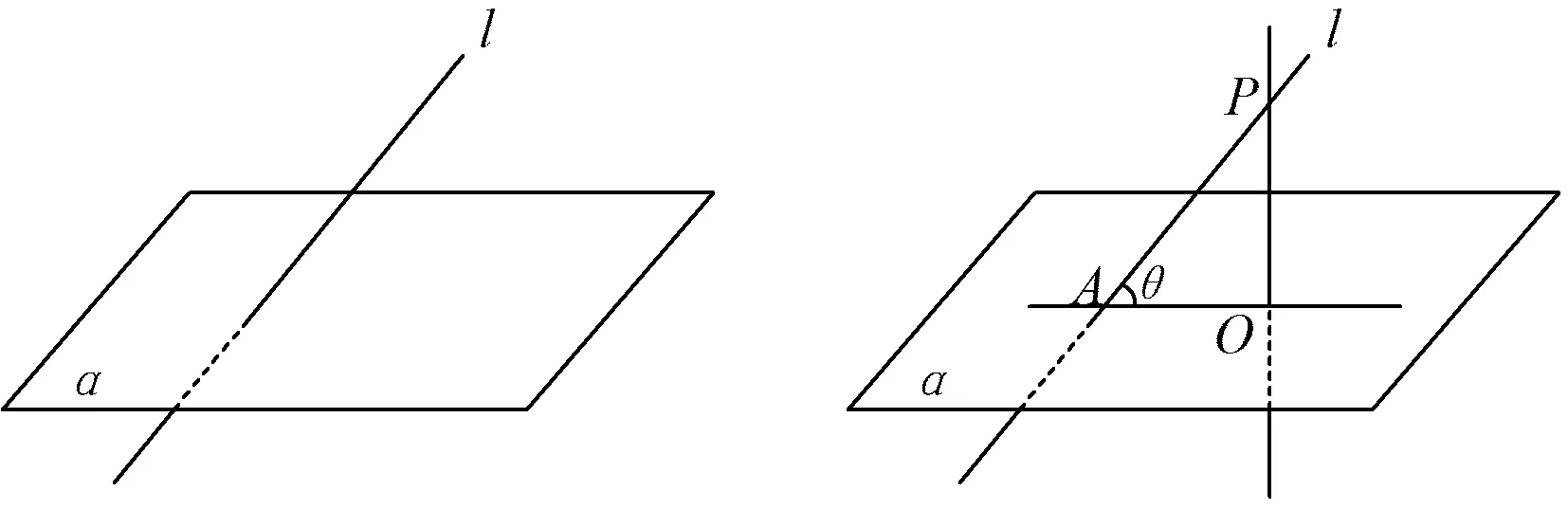
图2 图3

共同研究后，得出在直线l上任找一点P(如图3)，过点P作平面α的垂线PO(其中O为垂足)，则∠PAO就是直线l与平面α所成的角，即平面的一条斜线和它在平面上的射影所成的角，叫做这条直线和这个平面所成的角.

进一步，引导学生思考“如何界定一条直线与一个平面垂直”.这样的设计层层递进，首先通过观察旗杆与地面垂直的现象，发现旗杆与其在地面上的影子始终垂直，得出线面垂直的定义，并记此时线面角的大小为90°.再完成折纸探究，即如何翻折△ABC卡片，使折痕AD垂直于桌面，学生发现：当AD⊥BC，即在翻折过程中，AD⊥BD，AD⊥CD时，AD⊥平面BCD.由此猜想得到线面垂直的判定定理.最后通过类比线面平行，猜想与论证线面垂直的性质定理.

至此，从现实问题出发，通过“感知线面角(仰角)”到“一般化找线面角”，最后实现“精确定义和线面垂直判定”，在问题解决中一步步建构与完善概念，使学生深刻感受到数学学习的重要性.

4.1.3 模型建构

线面角本质上是运用平面化方法降维成一个线线角，用直线与其射影刻画该直线与平面的相对倾斜程度，那么“直线与它在平面内射影所成的角”和“直线与平面内任意直线所成的角”又具有怎样的关系呢？从而得出最小角定理：平面的斜线和它在平面内射影所成的角是这条斜线和这个平面内任一条直线所成的角中最小的角.这个关系的探索可以让学生先通过测量的方式进行初步判断，再通过几何画板演示等方法建立模型进行推理证明.

如图4，斜线AP在平面α内的射影为AO(其中PO⊥平面α)，作PB⊥AB，联结OB，则

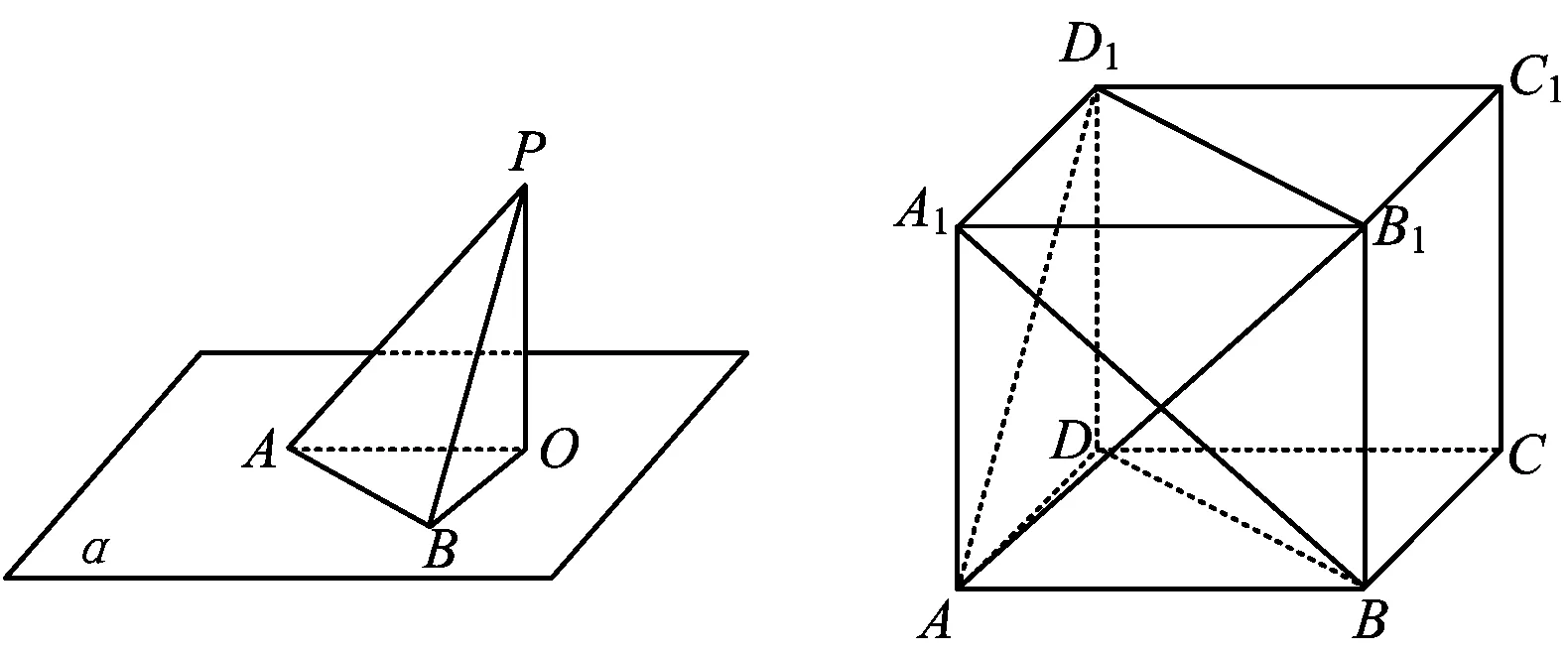
图4 图5

且

PO≤PB，

从而

sin∠PAO≤sin∠PAB，

于是

∠PAO≤∠PAB，

最小角定理得证.

4.1.4 联结应用

例2如图5，在正方体ABCD-A1B1C1D1中，

1)求直线A1B和平面ABCD所成的角；

2)求直线A1B和平面D1B1BD所成的角；

3)求直线AA1与平面AB1D1所成角的正弦值.

分析以正方体为载体进行线面角问题求解.通过求解可知，要找线面角，关键找线面垂直.

1)由AA1⊥平面ABCD可知直线A1B和平面ABCD所成的角为∠A1BA=45°.

2)取B1D1的中点O，易证A1O⊥平面D1B1BD，则A1B和平面D1B1BD所成的角为∠A1BO=30°.

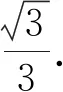
3个问题从易到难，步步递进，关注知识本质，促进概念理解和问题求解.

4.2 “第3课时：二面角(1)”的教学过程

4.2.1 问题聚焦

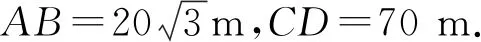
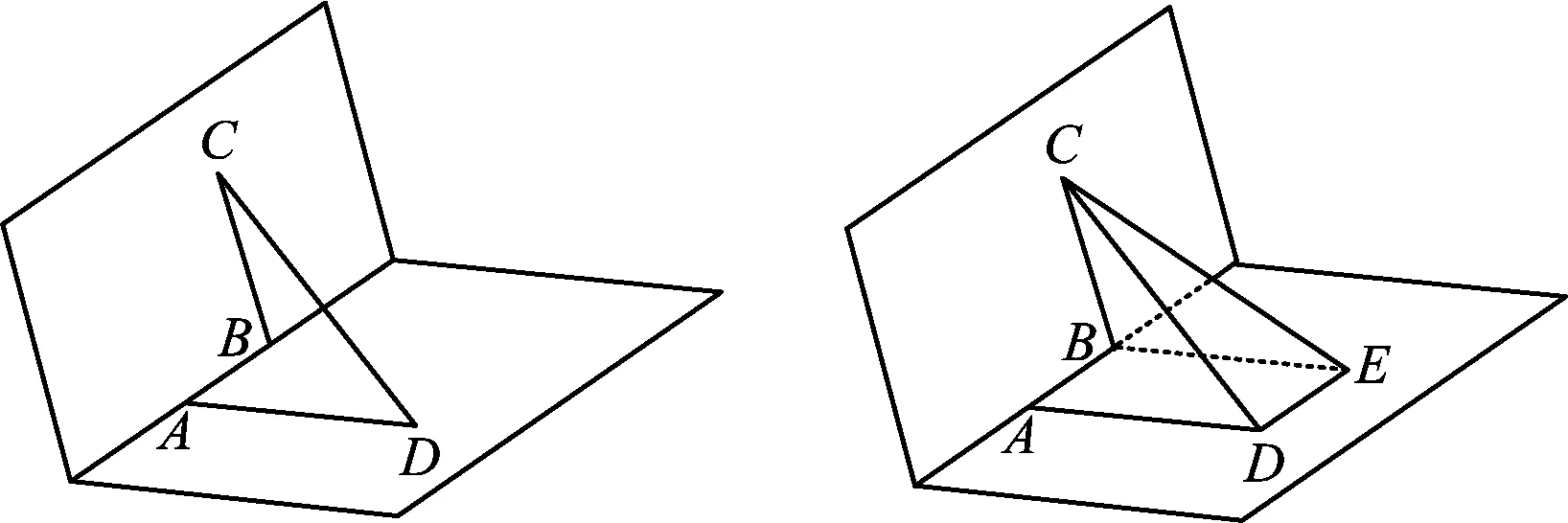
图6 图7

1)你认为如何刻画水坝与库底的相对倾斜程度？

2)尝试求库底与水坝所成角的大小.

学生先独立思考，再小组讨论，最后师生共研.学生普遍想到过点B作BEAD(如图7)，联结CE，用∠CBE的大小来衡量水坝与库底的相对倾斜程度，通过计算可求得∠CBE=120°.尽管没有学习过二面角以及二面角的平面角的概念，学生还是能够比较自然地找到用∠CBE来刻画大小，再一次说明了数学的自然性.

4.2.2 概念生成

通过水坝与库底的结构图，联系生活中翻书、开门等实际场景，抽象出二面角的概念以及用二面角的平面角来刻画相对倾斜程度.当二面角是直二面角时定义两个平面互相垂直，后续可类比面面平行去研究面面垂直的判定定理和性质定理，梳理出空间直线、平面垂直的线索.这个内容可以在下一课时独立完成学习.

4.2.3 模型建构

虽然“二面角的平面角”本质上也是用线线角刻画，但当我们逐步降维去看时，可以发现“二面角”可转化为“线面角”，“线面角”再转化为“线线角”.由此引发我们思考：平面内任意动直线与另一个平面所成角大小与二面角大小的关系，从而猜想和论证最大角定理：在一个锐二面角中，二面角是一个半平面内任意一条直线与另一个半平面内直线所成角的最大角.

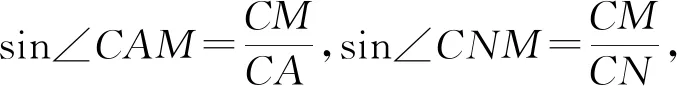
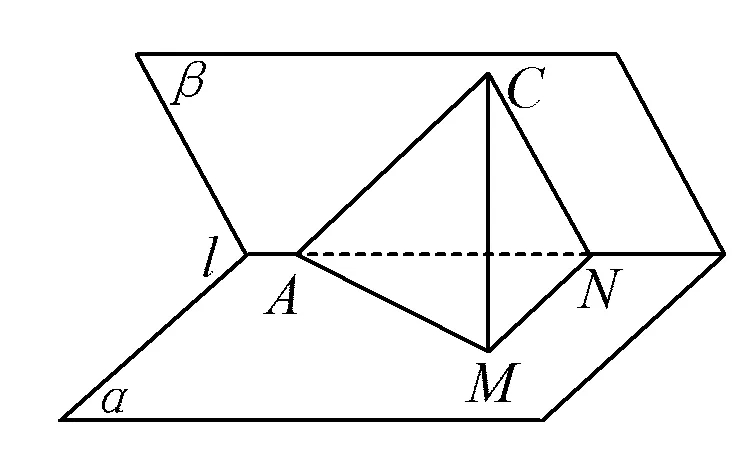
图8

4.2.4 联结应用

例4如图9，在正方体ABCD-A1B1C1D1中，求下列二面角的余弦值.

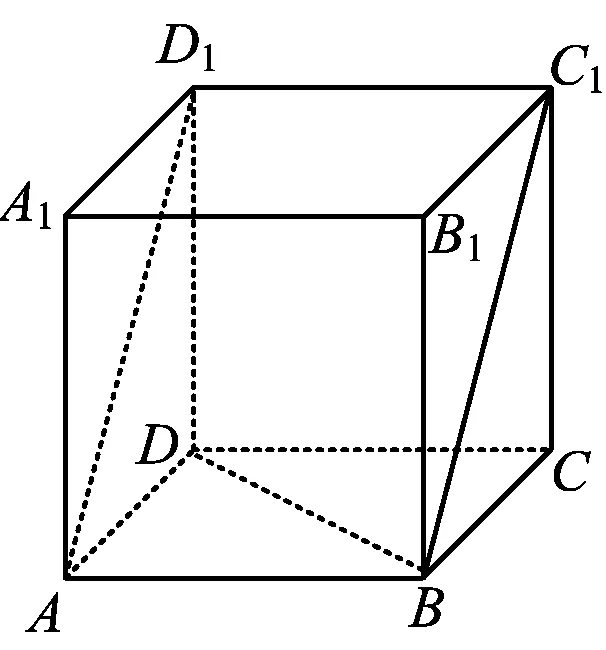
图9

1)二面角D1-AB-D；

2)二面角C1-BD-C.

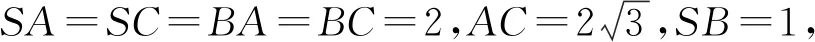
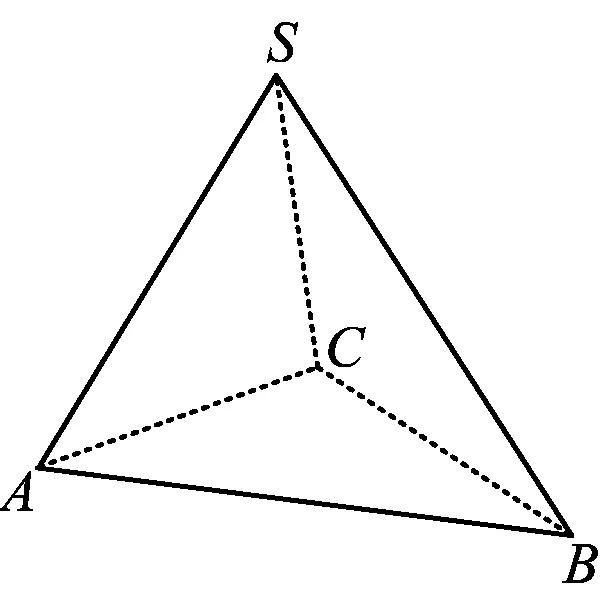
图10

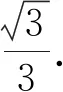
5 研究结论

5.1 增强学生的问题意识

“问题解决过程为线索”的设计模式，凸显了数学问题在数学学习中的价值，增强了学生的问题意识，进一步发展了学生“问题发现和提出、问题分析和解决”的能力.问题可以驱动思维，思维需要问题激励.以问题探究为学习起点，在问题解决过程中完善知识建构，激发学生的求知欲.如何结合情境设计能激发学生深度思考的核心问题是重中之重，因为它关乎学习任务的认知水平，直接影响学生在执行过程中的思维含量，指引活动的思考方向[2].“射击中仰角的大小”“水坝与库底之间夹角的大小”等，都是我们日常会面临和思考的问题，具有较强的典型性，引入到一般性思考就是刻画空间直线、平面的相对倾斜程度，这正是数学需要思考和解决的问题.通过本单元的学习，可以让学生发现空间三角的概念既有直觉上的合理性，又有数学推理中的严密性.

5.2 培养学生的数学大观念

数学学习的一个重要方面是帮助学生形成良好的数学观念，以数学大观念统摄数学学习.数学大观念是内容、过程和价值的融合，既包含对于核心内容本质的理解，也包括知识形成和应用过程中所体现出来的思想方法和思维方式[3].空间三角的学习，在问题提出和解决中要明确研究对象，建立数学概念，构建知识体系，提供一般化刻画的方法.特别是经历空间三角的学习，一方面，感悟一个概念抽象建构的完整过程，经历从感性到理性、猜想到论证的过程；另一方面，感悟空间角的升维和降维(升维指空间角的发展性，从线线角到线面角，线面角再到二面角；降维指空间角解决方法的平面化，从二面角到线面角，线面角再到线线角)，这也体现了事物的两面性.

5.3 利于学生形成知识结构

一节一节、一章一章地学习，尽管一定程度上也能达成夯实基础、提升技能的目标，但缺乏运用联系的观点看问题，容易使学生“只见树木，不见森林”[4].单元学习有利于将知识从零散走向系统，让知识建构通过一条问题解决的主线实现串联与迁移，帮助学生学会学习.平面化将空间三角紧密联系在一起，通过“问题聚焦、概念生成、模型建构、联结应用”建立起了空间角的学习线索，在问题解决过程中生成了相应的垂直概念，又通过类比空间直线、平面平行得到了空间直线、平面垂直相应的判定定理和性质，形成良好知识网络结构图(如图11).

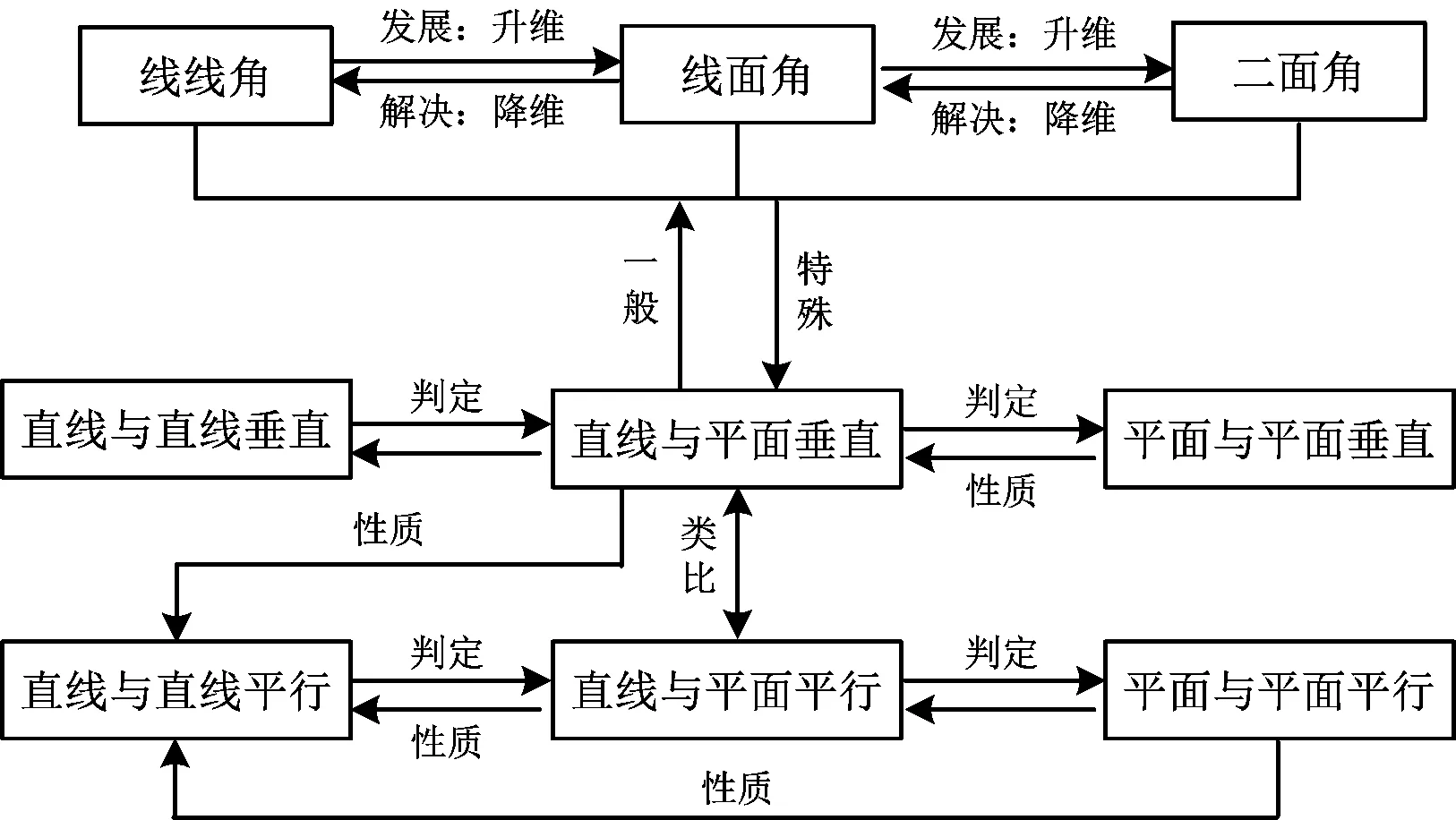
图11