计及SSSC的高渗透率新能源电网静态电压稳定特征研究

郑亮，马道广，周霞，戴剑丰

（1.国电南瑞科技股份有限公司，南京 211000；2.南京邮电大学 先进技术研究院，南京 210023；3.南京邮电大学 自动化学院、人工智能学院，南京 210023）

0 引言

中国在第七十五届联合国大会上提出，采取更加有力的政策和措施，力争2030年前二氧化碳排放达到峰值，努力争取2060年前实现碳中和的目标［1］。目前，以新能源为主体的新型电力系统得到广泛应用，大规模新能源呈现高比例并网的发展趋势。在高渗透率新能源并入电网发电场景下，解决大规模新能源发电时的不确定性给电力系统安全稳定运行带来的挑战，是当前研究人员重点关注的问题，其中静态电压稳定问题尤为显著［2—3］。

针对解决新能源并入电网后的静态电压稳定问题，目前也有较多的文献利用分析静态电压稳定特征的方式量化系统电压稳定性，同时提出提升静态电压稳定性的策略。传统静态电压稳定特征分析是以潮流计算为基础，通过寻找静态电压稳定临界点，计算得到当前系统节点的电压稳定裕度，常用的有连续潮流法［4—5］、崩溃节点法［6—7］和非线性规划法［8］。文献［9］基于节点电压曲线、无功功率变化曲线，将系统临界稳定运行的节点电压变化值和无功功率变化值加权和作为综合电压稳定指标，评估内部负荷变化时电力系统的电压稳定性。文献［10］根据输电线路上功率与线路首尾节点电压之间的关系，利用潮流计算方程根的判别式提出静态电压稳定指标。文献［11］按照简化系统思路和分析配电网的单条线路模型，在潮流计算的基础上，针对配电网安全稳定问题提出静态电压稳定指标。但现有的静态电压稳定指标大多是基于单一固定的模型进行设计，忽略了负荷波动、新能源发电不确定性等因素，难以充分反映当电力系统受到扰动后整体的运行状态，限制了静态电压稳定指标的通用性。伴随着电力电子器件的发展，柔性交流输电技术（flexible AC trans-mission system，FACTS）在调节线路潮流、改善静态电压稳定性方面的研究更加深入［12—13］。文献［14］分析了高比例光伏并入电网对系统安全稳定运行的影响，并提出通过对新能源电网配置FACTS装置的策略改善系统薄弱线路静态电压稳定性。文献［15］通过安装TCSC和STATCOM装置在电压薄弱节点处，调节线路潮流从而提升系统整体静态电压稳定性的方案。上述文献中的不足之处是没有将FACTS装置与电力系统潮流计算方程结合提出新的电压稳定指标，并且未考虑新能源电网配置FACTS装置后对电力系统安全稳定运行性的提升。静态同步串联补偿器（static synchronous series compensator，SSSC）作为目前先进的柔性交流输电装置之一［16—17］，为电网的安全运行提供了一种电压支撑和功率调节的方法，SSSC通过调节线路潮流稳定的有效缓解高比例新能源接入电网后对系统安全运行所带来的危害［18—19］。

针对以上存在的问题，本文探讨了SSSC对高渗透率新能源电网静态电压稳定特征的影响，从系统静态电压稳定性方面评估SSSC发挥的控制潮流效能。为研究配置SSSC的潮流控制效能对系统静态电压稳定性的提升，本文首先通过等值功率注入法对SSSC装置建立等效模型，得到基于SSSC的潮流计算方程；然后针对新能源并入电网后所带来的安全稳定性问题，利用潮流计算方程提出相应的系统静态电压稳定性指标，分析不同容量新能源并入电网后配置SSSC对当前电力系统薄弱节点静态电压的影响；最后通过IEEE-24节点分析SSSC的潮流控制效能对系统静态电压稳定特征的影响。

1 SSSC数学模型

1.1 SSSC基本原理

图1为SSSC的基本原理图，其中Use为SSSC的等效电压源；Zlm为SSSC的等效阻抗；UDC为逆变器电压；Ii为母线电流。图1中SSSC装置是通过串联变压器接入电网母线，包括电压源逆变器以及电容器，SSSC通过向接入节点注入一个幅值可变、相角与电流垂直电压的方式，达到改变输送线路功率、调节线路潮流的作用。

图1 SSSC的基本原理图Fig.1 Basic schematic diagram of SSSC

1.2 SSSC等效电路

SSSC的等效电路图如图2所示，其中Us为系统等效电源；XSSSC为单匝变压器等效漏抗；USSSC为SSSC等效电压源；ILine为系统电流；UL为负载侧电压，Yse=Gse+jBse为串联变压器的等效导纳。

图2 SSSC的等值电路图Fig.2 SSSC equivalent circuit diagram

节点i的电压电流关系可以描述如下

已知YL=GL+jBL，Y=jB，由此我们可以得出由和表示的Ii和Ij如下

将yii和yjj分解成两部分：yii=-yij+yi0和yjj=-yij+yj0，则有

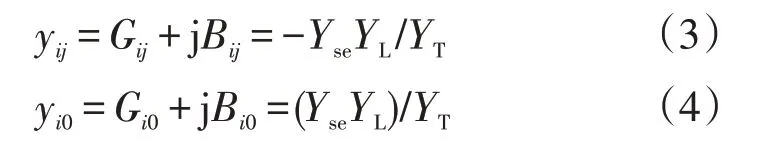
在电力系统中，一般采用节点注入功率的方式将系统等效为如图3所示的等值功率注入形式，其中

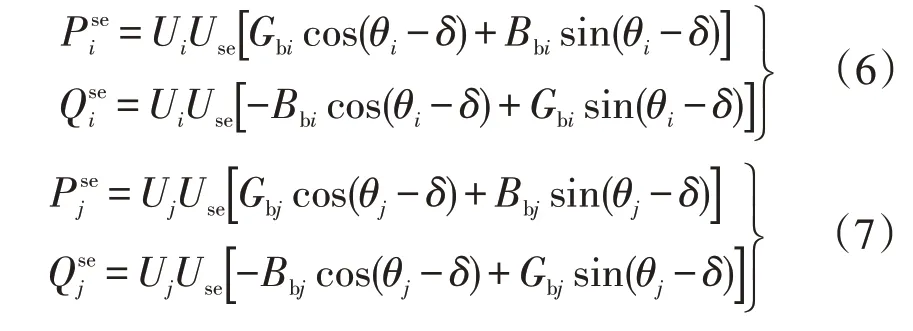
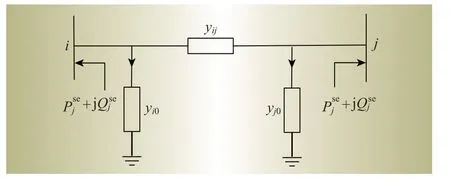
图3 SSSC的等值功率注入Fig.3 Equivalent power injection of SSSC

2 考虑新能源的系统静态电压稳定分析

2.1 新能源发电等效模型

以风电机组为例，其并入电网的数学模型如图4所示。其中XS为输电线路阻抗；U为并网母线电压；PL、QL为负荷的有功功率及无功功率。

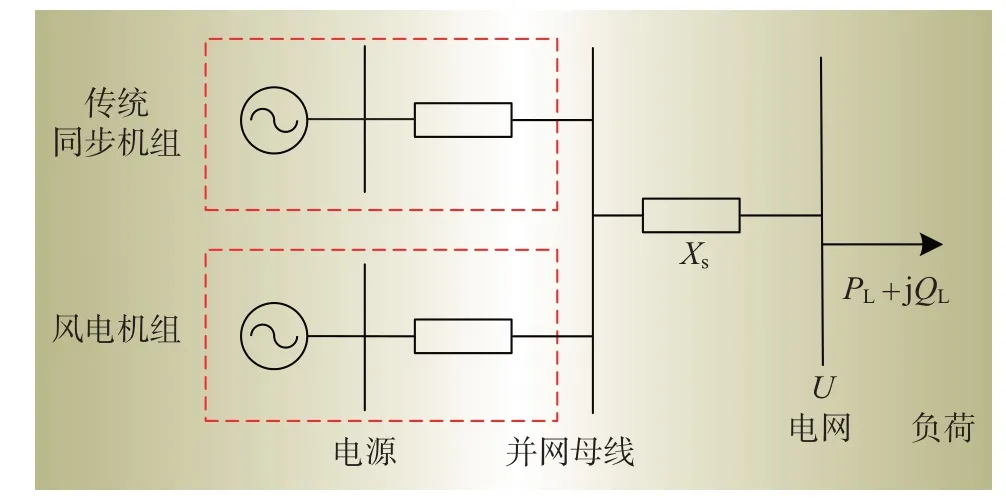
图4 风电并网数学模型Fig.4 Mathematical model of wind power integration

XS′G、XW′分别为传统机组、风电机组到并网点的等值阻抗，计算如下

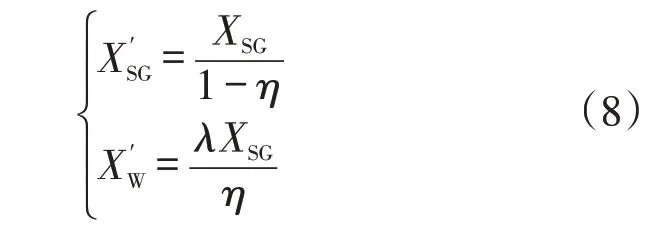
式中：XSG为当系统中仅有传统机组并网时的系统等值阻抗；η为风电渗透率，定义为风电出力。假设机组容量与等值电抗比值为定常数，λ为风电发电机组与传统机组至同一并网点的阻抗比值。

2.2 新能源接入系统的静态电压稳定机理

以风电、光伏为代表的新能源发电机组是通过P、Q进行解耦控制来实现电压的灵活可控的，在实际电网运行中受逆变器容量的限制，并入电网的新能源通过解耦控制策略对P、Q进行解耦控制。风电场和光伏电站的静态电压稳定机理一致，新能源接入电网的简化图如图5所示。其中US为电网平衡点电压；UC为风电/光伏接入电网点电压；RS+jXS为并入电网的等效阻抗；PW+jQW为风电场的功率和无功功率；I为风电场的电流。

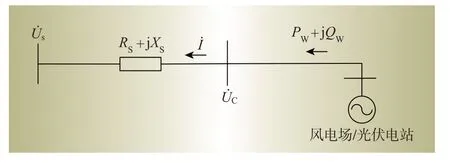
图5 新能源接入电网的简化图Fig.5 Simplified diagram of new energy access to power grid

新能源接入电网后的静态电压稳定分析如下

新能源并网点向电网发出功率后

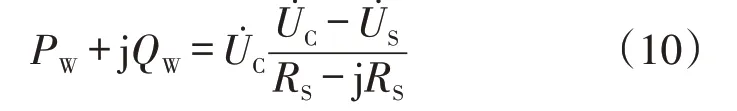
其中

化简后可得

忽略传输电阻RS，可得

由式（14）可知，新能源并入电网功率与接入电网的电压之间成负相关，随着新能源功率的增加，电网有功功率与节点电压相关联的灵敏度逐渐增大，系统电网的电压稳定性明显降低。

3 含SSSC的系统静态电压评估

对于任何复杂的电力系统，都可以简化为包含n个节点，m-1个PQ节点，n-m个PV节点，以及一个平衡节点的系统，潮流平衡方程可以表示为

简化后的潮流平衡方程为

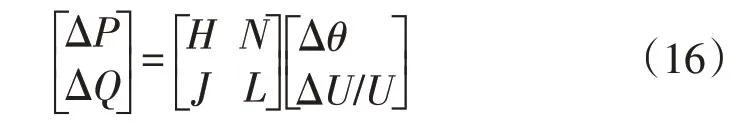
式中：ΔPi为系统第i个节点有功注入功率量；ΔQi为系统第i个节点无功注入功率量；Ui为系统第i个PV节点电压值；Gij、Bij分别为i-j支路导纳的实部和虚部。

3.1 计及SSSC的潮流计算方法

将SSSC配置在线路i-j的节点i侧，并且对配置SSSC所在线路两端的潮流方程进行更新，其它节点潮流计算方程保持不变。系统更新后的潮流计算方程为

式中：Pi(in,i)、Qi(in,i)、Pj(in,j)、Qj(in,j)分别为SSSC注入系统节点i、j的有功和无功功率。

3.2 系统静态电压稳定指标

对于任何电力系统而言，其支路模型都可以简化为如图6所示。其中支路i节点首端电压为Ui；末端节点电压为Uj；R+jX为支路阻抗；Bc为对地导纳；P、Q分别为支路末端的有功、无功功率。

图6 输电网简化模型Fig.6 Simplified model of the transmission network

相应电压方程如下

式中：c1=a12+a22；c2=2(a1b1+a2b2)；c3=2(a1b2-a2b1)；c4=b12+b22。令x=Uj2，可得ax2+bx+c=0，其中a=c1，b=(c2P+c3Q-Ui2)，c=c4(P2+Q2)，因此可得

故节点j电压稳定的条件是Uj有实数解。系统处于临界稳定时两个根达到同一个值临界电压Ujeq，此时Δ=(b2-4ac)=0。因此可得

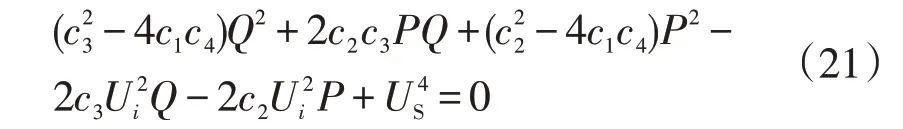
则曲线上的点为Qcr和Pcr。设x=Q，y=P，则有

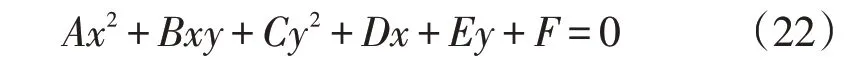
电压安全稳定曲线如图7所示，此曲线的横、纵坐标分别是系统输电线路上的无功功率、有功功率，(x1,y1)是系统的运行状态，因此本文的电压稳定安全裕度可以表示为

图7 安全稳定运行曲线Fig.7 Safe and stable operation curve

令系统初始(Q0,P0)为(x0,y0)，系统临界稳定运行功率(Qcr,Pcr)为(x1,y1)。代入方程对x求导可得2Ax+By+Bxy′+2cyy′+D+Ey′=0，又由于所求(x1,y1)为到(x0,y0)的最短距离，所以化简后可得运用Matlab求解即可从(x1,y1)得到(Qcr,Pcr)。

SSSC装置通过调节线路潮流的方式改善系统静态电压稳定性。线路末端负荷节点j电压稳定值可表示为

式中：N为系统中以j为节点末端的支路总数。系统在不同运行状态下的最小节点电压稳定裕度被定义为系统最薄弱节点，此节点安全裕度的大小能体现系统整体的静态电压稳定性，即

式中：k为系统中负荷节点的个数。

4 算例分析

新能源接入的IEEE-24节点系统如图8所示。

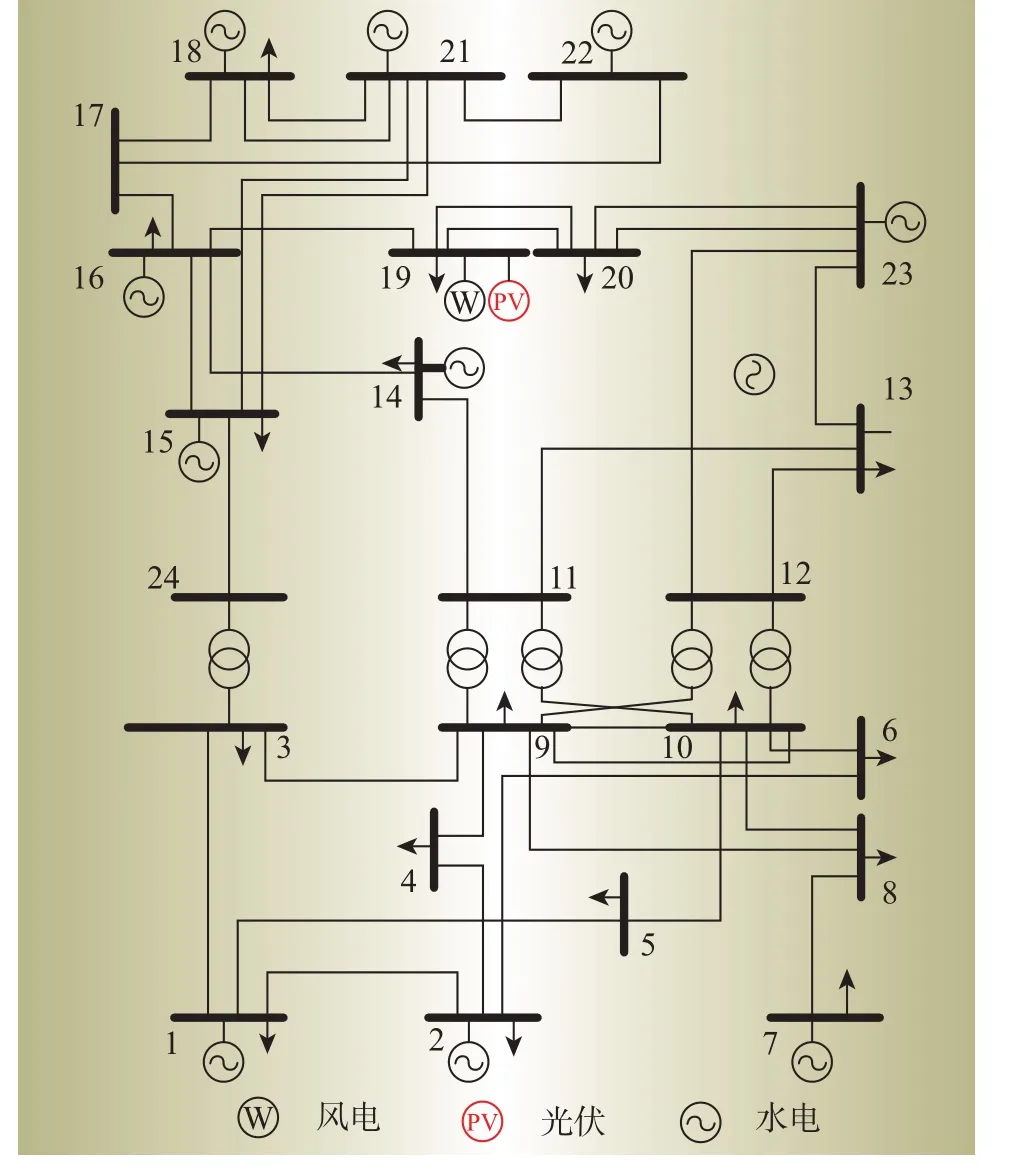
图8 新能源接入的IEEE-24节点系统Fig.8 IEEE-24 node system for new energy access

本文以风电、光伏为代表的新能源接入的IEEE-24节点系统为例，采用MATPOWER工具包进行仿真分析，验证本文所提指标的正确性和合理性。此外，本文采用负荷、发电机运行方式如下：

（1）负荷以恒定功率的方式增长。

（2）发电机或新能源的出力增长方式以初始基准值等比例增长。

（3）当发电机或新能源无功功率超出安全界限后，无功出力固定为其最大无功出力值，并将当前新能源并网节点转变为PQ节点。

设置场景如下：关键节点的有功和无功负荷以恒定功率因数的方式增长，发电机和新能源以初始基准值等比例承担负荷增长。再使得新能源电源逐渐替代发电机节点电源，研究不同接入点对关键节点静态电压稳定的影响。

图9为本文所使用的IEEE-24系统在初始状态下各节点静态电压稳定值。

由图9可知，19节点在初始运行状态下的值为0.331 5，该节点电压安全稳定裕度最小，在整个系统中处于最薄弱位置。

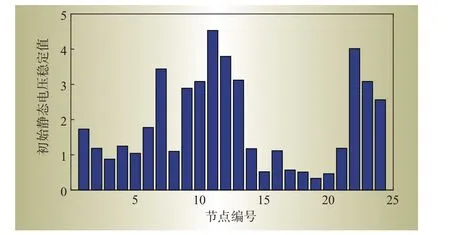
图9初始状态下的各节点静态电压稳定值Fig.9 Static voltage stability values of each node in initial state

4.1 不同渗透率新能源对静态电压的影响

图10所示为新能源渗透率增长过程中不同节点的电压稳定值。

图10新能源渗透率增长过程中不同节点的静态电压稳定值Fig.10 Static voltage stability values of different nodes in the process of new energy penetration growth

由图10可知，系统接入新能源后影响整个系统的安全稳定性，其中新能源节点19处的静态电压稳定值下降了0.075，节点15处的静态电压稳定值下降了0.058 8，这表明距离新能源负荷节点越近电压下降速率越快。

4.2 SSSC对静态电压稳定性的影响

4.2.1 不同配置地点的结果对比

以薄弱节点19为例，本文以节点19处接入SSSC的方案为基础，研究分析在不同薄弱节点处以及不同安装位置下系统的静态电压稳定结果，表1为不同配置地点的结果对比。

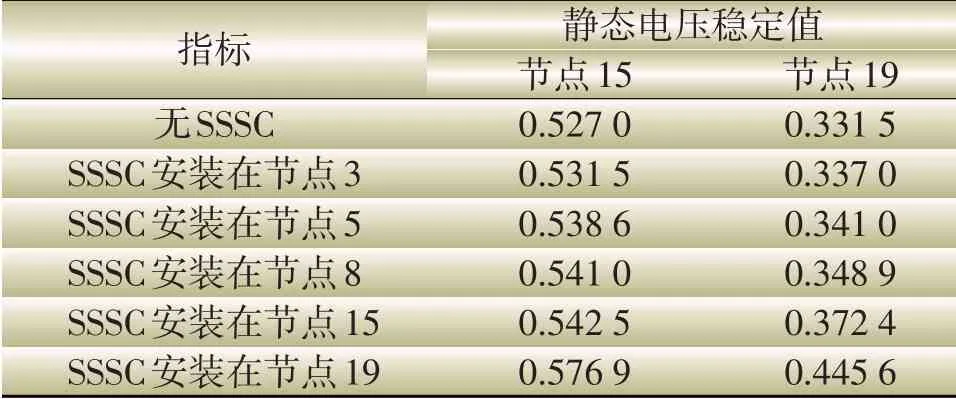
表1 不同SSSC配置地点的静态电压稳定值Table 1 Static voltage stability values at different SSSC configuration locations

由表1可得，无论是否接入新能源，SSSC均能提升电网整体的静态电压稳定性。将容量为70MVA的SSSC配置在节点19处后，线路16-19阻塞处潮流减小，且由线路16-19组成的送端断面功率逐渐减小，系统静态电压稳定指标值增加，系统静态电压稳定性增强。相比于将SSSC装置安装在其他薄弱节点（节点3、5、8、15），当系统在最薄弱节点19处安装SSSC对整体电压稳定性的改善更加明显，静态电压稳定值提升了0.114 1。结果表明，SSSC对潮流的控制能力与接入薄弱节点位置的距离成正相关，距离薄弱节点越近SSSC装置调节支路潮流的能力越强，同时可降低扩建输电设备的投资，增强新能源电网运行时的安全性与经济性。

4.2.2 不同配置容量的结果对比

为进一步对比分析SSSC设备容量对系统静态电压稳定性所带来的影响，本文在薄弱节点15和节点19处分别接入不同容量的SSSC，并且与系统未接入SSSC时的静态电压稳定结果进行对比分析，不同容量下系统薄弱区域线路静态电压稳定值如表2所示。

表2 不同容量下系统薄弱区域线路静态电压稳定值Table 2 Static voltage stability value of line in weak area of system under different capacity

由表2可得，随着配置在系统薄弱节点处SSSC设备容量的增加，由系统重载线路16-19组成的送端断面功率逐渐减小，静态电压稳定值逐渐提升，系统静态电压稳定性增强。同时当SSSC的安装容量达到100 MVA时，相比于不安装SSSC时静态电压稳定值提升了0.120 6。这表明在系统的薄弱节点处增加接入的SSSC设备容量，将会提升支路潮流精细化控制能力，SSSC利用等效功率注入法将阻塞线路处潮流转移至其余相对空闲输电通道，充分利用线路传输容量、优化整体潮流分布从而提升电网整体的安全稳定性。

4.2.3 不同运行方式下的结果对比

为适应实际电网复杂的运行环境，本文根据经验以及历史运行数据等相关资料模拟新能源经典应用场景（夏季光伏大发、冬季风电充足），分别选取不同的运行方式调整SSSC的配置方案。本文为模拟两种场景下的运行方式，选取第二种运行方式令230 kV节点处的负荷增加10%，138 kV处的节点负荷减少10%，表3为不同运行方式下典型节点19的系统静态电压的改善效果。

表3 不同运行方式下的系统静态电压稳定性Table 3 System static voltage stability under different operation modes

由表3可得，系统处于两种运行方式下，SSSC均能提升电网整体的静态电压稳定性。将容量为70 MVA的SSSC配置在节点19处后，当系统运行在负荷波动较大的场景下，系统薄弱节点19处静态电压稳定性增强，SSSC在不同运行方式下分别提升系统静电电压稳定值0.114 1和0.126 0。SSSC可以根据新能源、负荷的变化灵活调整分布注入功率大小提升系统静态电压稳定性。

5 结束语

本文分析了SSSC对高渗透率新能源电网系统静态电压稳定性造成的影响，从系统静态电压稳定性方面评估SSSC发挥的控制潮流效能。结论如下：

（1）高渗透率新能源并入电网后系统静态电压稳定性下降，SSSC通过注入功率的方式调节薄弱节点电压，可有效提升新能源电网的安全稳定性。

（2）对当前系统运行状态进行静态电压稳定分析，在系统薄弱节点安装SSSC能更好的提升整体安全稳定性。

（3）安装SSSC在薄弱节点处可有效降低扩建输电设备的投资，提升新能源电网运行时的安全性与经济性。D