步态数据挖掘在爬壁机器人路径规划中的应用

杨 云，魏秀卓，赵 艳

（1.长春教育学院信息教研室，吉林 长春 130052；2.长春人文学院理工学院，吉林 长春 130117；3.长春师范大学教育学院，吉林 长春 130123）

1 引言

爬壁机器人因其垂直立面作业的特性，属于一种特种作业机器人，例如油罐、桥梁等建筑物的检测，高层建筑物壁面清洁等，甚至会用到反恐侦察这类特殊工作上。由于爬壁机器人不同于水平面行走的机器人，所以对其行走的路径需要作出更具体和完善的规划，以保证爬壁机器人能够安全行走的同时高效工作。

由于爬壁机器人在立面极限作业的情况下，危险性以及耗能都相当之高，因此针对爬壁机器人进行路径规划时，应尽量减少其与障碍物相遇甚至是产生碰撞的情况，最大限度的保证机器人的安全性。同时因为壁面爬行不同于水平行走，机器人受到重力、摩擦力等因素的影响，其灵敏度以及越障能力都会有所下降，因此在路径设计时，主要考虑路径的长度问题，路径是否平滑以及对障碍物的规避是否有效。例如，文献［1］通过电势场法，降低环境复杂度并对其利用电路流通能够快速地获得搜索路径并平滑处理，但没有考虑到动态障碍物对机器人的行走路线的影响；文献［2］利用免疫优化算法，根据障碍物实际情况建立地图模型，采用精英保留策略加强局部搜索，但其搜索时间较长，对机器人的反应速度有限制。

为此这里通过对越障步态数据的挖掘，研究出了一种适用于爬壁机器人的实时路径规划方法，在蚁群算法的基础上加入避障因子，通过蚁群信息素的更新迭代找到最优路径，并利用障碍规避策略对实时可能产生的障碍物进行探测和规避，最终将路径曲线进行平滑，减少爬壁机器人行走时的能耗，使能够安全、无碰撞地完成作业。

2 爬壁机器人越障步态数据挖掘

根据数据挖掘原理，利用关联规则挖掘爬壁机器人越障步态数据。在爬壁机器人工作环境中，定义任意一个数据项均为候选项集的集合F1中的元素，扫描数据库并利用式（1）得到F1中各元素的支持度。

式中：c(f1∪f2)—障碍数据f1，f2同时出现概率值；|D|—关联规则挖掘的越障步态数据集。设η—最小支持度阈值，在F1中选择支持度不小于η的项集组成越障步态数据频繁项集为L1。根据生成的关联规则将其裁剪得到压缩过后的C3。之后再一次遍历越障步态数据库，并得到F3中各元素的支持度。在F3中挑选支持度不小于η的项集组成越障步态数据频繁项集的集合L3。最后对L3进行自连接，以数据包的形式输出爬壁机器人越障步态数据的挖掘结果。

3 爬壁机器人路径规划

3.1 蚁群算法最优路径选择

蚁群觅食时会对搜索路径释放本身独有的信息素，大量蚁群在不断搜索的过程中，经过最优路径或是折点的概率加大，从而这个地方会有很多蚂蚁分泌的信息素，蚁群最终会根据信息素的数量来选择最优路径，信息素的数值越高代表经过此路径的蚂蚁越多且路径有效。蚁群初始搜索时，信息素会分布不均匀，搜索时间以及路径都比较长，这里对搜索范围作出限制，并将蚁群迷路的情况排除，最终将没有迷路的蚁群信息素更新利用，寻找最优路径。

以上述得到的越障步态数据数据包为基础，为了使蚁群搜索路径保证在可控范围内，在矩形地图的基础上设定S、T两点分别作为蚁群的出发点和目标点，并将这两点作为对角顶点在矩形地图内设置一个有效区域地图，并增加该有效区域内的信息素数值，具体如下：

式中：τ0—矩形地图内信息素初始数值；C—常数且大于τ0；x—地图序列号；R—矩形地图内有效区域。

为了避免蚁群在地图上盲目搜索，这里对整个矩形地图的初始信息素分布作出调整，如图1所示。从图1可以看出最优路径应为S点到T点这个方向上的路径，因此由出发点S和目标点T作为对角顶点的矩形地图内蚁群信息素初始数值设定为C，地图其他区域信息素数值不变，这样不仅可以减少蚂蚁盲目搜索产生的无用路径，也可以减少搜索时间提高效率。

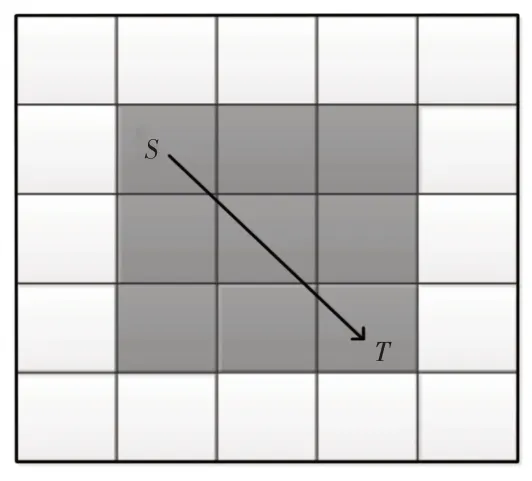
图1 信息素初始值分配Fig.1 Pheromone Initial Value Allocation

蚁群在刚开始搜索阶段可能会产生很多的交叉路径，且会有一部分蚂蚁出现迷路的现象，迷失过程中没有走到终点就停止了搜索并停留在最后搜索到的路径原地打转，这时对于搜索而言效率极低，尤其是在地图面积扩大或者是障碍物增加的时候，这种情况会更加严重，最终使算法不够精准且收敛速度较慢。而蚁群搜索是通过多数蚂蚁不断对路径进行搜索而最终筛选出来的择优路径，所以当前期搜索的结果越多且搜索质量越好时，最终得出最优路径的概率越大，而且收敛速度会比较快，而蚁群搜索过程中个别蚂蚁会迷路且停滞打转的原因在于周围各个路径节点都已经走过了且存在障碍物无法通过，所以在蚁群搜索初期本问通过越障步态数据挖掘，利用避障策略［3］，增加避障因子safetyj。则蚂蚁选择一个节点到另一个节点转移的概率可以表示为：

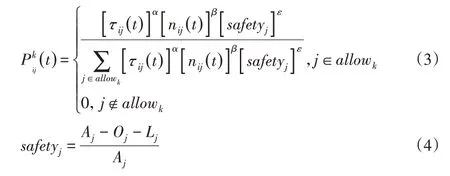
式中：t—路径筛选次数；k—任意一只蚂蚁；i、j—不同搜索节点；τij—从i～j这条路径上信息素的浓度；nij—针对蚂蚁给出的启发信息；allowk—蚂蚁能够到达下一个节点的路径集合；α—信息素的重要程度；β—信息素对蚂蚁寻路的指导程度；Oj—和j相邻且有障碍物的栅格数量；Lj—和j相邻但无法通过的栅格数量；Aj—栅格总数；ε—避障系数且为正。

增加避障策略能够使蚁群在筛选搜索路径时进入迷路停滞状态［4］的概率减小，此时：

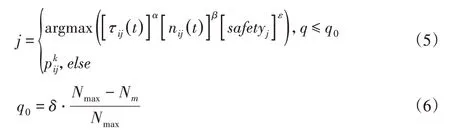
式中：Nmax—最大筛选次数；Nm—当前的筛选次数；δ—取值范围在（0.5，1）的调整系数。

当q0在初始阶段取值较大时，蚂蚁能够通过对整个地图的路径搜索找到相对比较有利的路径，经过这个阶段，再将q0的取值调小，有利于蚁群对路径的随机搜索。

每经过一次搜索路径的筛选后，将能够到达目标点的蚂蚁信息素进行更新保留，从而将未能到达目标点、迷路停滞的蚂蚁剔除，来保证信息素的有效性，如式（7）所示。

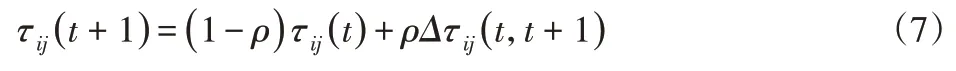
式中：ρ—信息素的挥发程度，ρ∈(0，1)；Δτij—蚂蚁在路径(i，j)上信息素的增量变化；t—时间。

同时为了让信息素保持优化，对全局信息素作出基础择优规划，分别对优质蚂蚁和劣质蚂蚁所经过路径的信息素做加强和减弱处理，为避免信息素不均匀对搜索产生过大影响，对其进行浓度限值，即，设λ—信息素的增加比例，且大于0小于1，如式（8）所示：

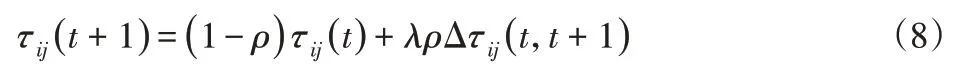
对信息素挥发程度ρ作出相应调整［5］，经过多次筛选蚁群算法的路径最优解都是同一个的情况下，这时需要避免结果是陷入局部最优循环而得出，对ρ作出如下调整：

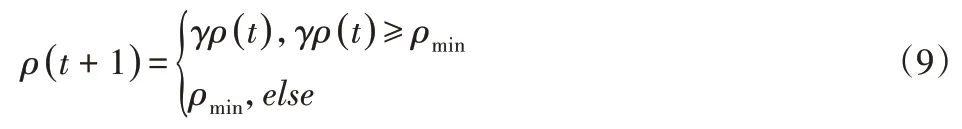
式中：γ—信息素衰减系数，且在（0，1）范围内，如果调整信息素后，连续多次路径筛选的结果都小于历史最优解，此时应按照式（6）更新信息素，得出最优搜索路径。

3.2 路径障碍动态规避

由于蚁群算法找到了最优路径，爬壁机器人会按照既定路线进行作业，但在墙面作业时，不能保证不出现墙面脱落或是高空飞物等障碍，这时爬壁机器人不能实时地应对突发障碍而作出有效判断并改变既定路线，而针对这一缺陷这里在蚁群搜索得出的最优路径上进一步设计了障碍规避策略，给爬壁机器人安装声呐数据装置，当遇到障碍物时其斥力与合力如下：

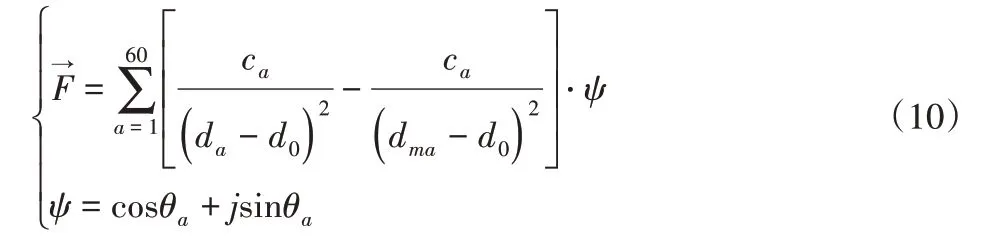
式中：ca—机器人与障碍物的距离比例；da—声呐装置发出第a个探测波与障碍物之间的距离；d0—爬壁机器人在墙面作业时与障碍物间安全距离；dma—声呐的探测波m最大探测距离；ψ—合力角度；θa—第a个探测波的探测角度。

式中：s—机器人执行的躲避动作；r—动作相对应的参数，求出(s，r)的最大Q值并对目标信号做强化趋近处理。对信号强化处理设置可控制范围：

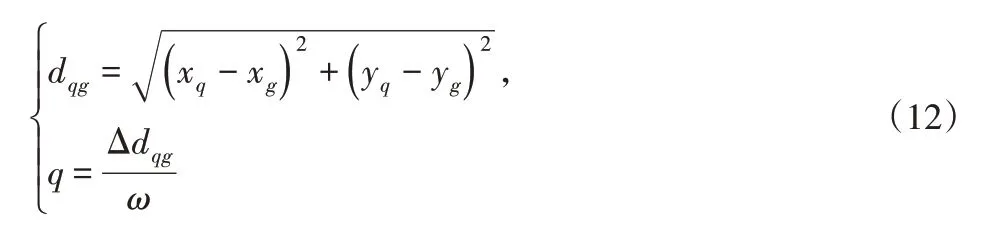
式中：(xq，yq)—爬壁机器人所在位置坐标；

(xg，yg)—爬壁机器人下一目标位置坐标；

dqg—两者之间的距离；

Δdqg—爬壁机器人位移差；

ω—爬壁机器人移动一次的长度；

q—信号强化的控制范围，通过对信号强范围的控制得出机器人躲避障碍物的动作范围并得出规划路线。

4 路径平滑处理

经过蚁群择优路径和障碍物规避策略，基本路径已经确立，但经过蚁群算法规划的路径转折点较多，路径不平滑，这时要考虑的是机器人在爬壁过程中路径的转折次数对机器人爬壁作业的影响，对其进行平滑处理，减少机器人爬壁路线的折点，并基于以上过程规划最终路径。这里利用贝塞尔曲线［7］对路径进行描述，并连接路径转折点进行平滑处理，其表达式为：

式中：P(u)—曲线运动轨迹控制点；

P(f)—位置描述点；

P(0)—曲线的起点；

P(1)—曲线的终点，所有描述点最终组成一个特征描述多边形；

Bf，n(u)—n次多项式，且：

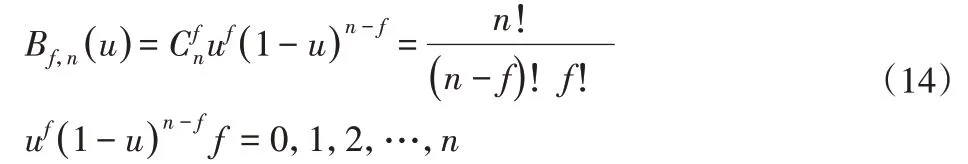
当n=1时，曲线为一阶且为一条直线，有两个描述点，当n=2时，曲线为二阶且为一条抛物线，当n≥3时，曲线属于高阶且有n+1个描述点。通过函数分析求解曲线：

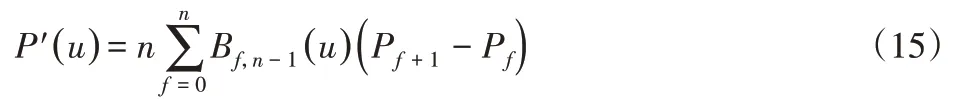
基于贝塞尔曲线起始点和多边形的起始点是相同且方向一致的，那么当曲线特征多边形确定的时候其形状也就跟着确定，并不受其他因素影响，基于以上算法，可以对路径作出平滑处理［8-10］和最终规划。具体规划算法如下：

（1）利用栅格法建立初始地图，确定算法参数和爬壁机器人的出发点与目标点；

（2）令蚂蚁K从出发点开始搜索路径，经参数控制得到下一个移动点；

（3）判断蚂蚁是否到达目标点，若达到则设置k=k+1令所有蚂蚁均在这一步骤完成对路径的搜索并初步筛选；

（4）通过蚁群中所有蚂蚁的路径搜索结果筛选出蚁群算法最优路径，并对信息素值做调整最终得出优化路径；

（5）判断算法是否满足退出条件，若满足则输出最优路径，反之则转至1）；

（6）对蚁群算法得出的最优路径加入声呐动态避障策略；

（7）对最终路径平滑处理。

根据上述规划算法，得到具体规划流程，如图2所示。

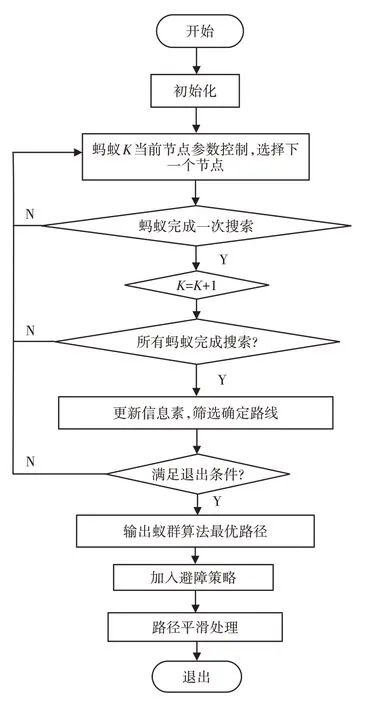
图2 蚁群算法流程图Fig.2 Flow Chart of Ant Colony Algorithm

5 实验

为验证这里路径规划方法对越障爬壁机器人的有效性，对电势场法、免疫优化算法和这里方法进行对比实验，从最优路径、迭代次数以及算法用时三个角度进行对比。

5.1 爬壁机器人工作环境建模

这里方法所研究的爬壁机器人工作环境为高层建筑外墙面，因此首先建立爬壁机器人工作环境三维模型，如图3所示。

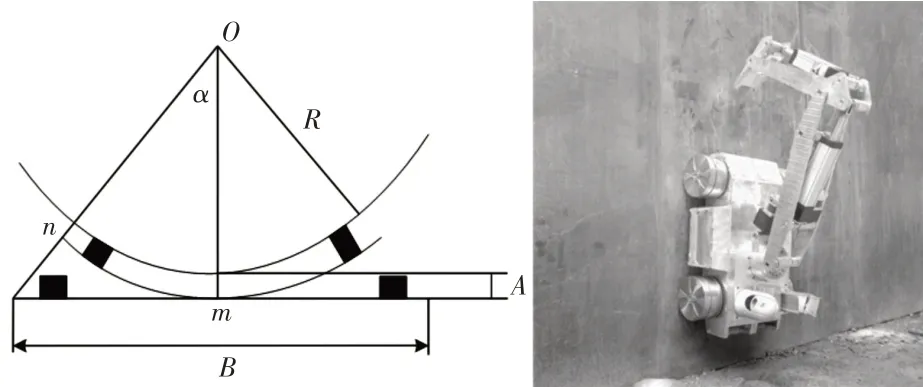
图3 爬壁机器人工作环境三维模型Fig.3 Three Dimensional Model of Working Environment of Wall Climbing Robot

图中：O—高层建筑横截面圆心；R—高层建筑半径；n—爬壁机器人左端点；m—爬壁机器人质心；A—爬壁机器人底板距高层建筑外壁距离；B—爬壁机器人宽度；α—机器人爬行后的曲率角。

5.2 规划路径曲线图整体效果分析

以图3为基础，建立地图模型，使势场法（文献［1］）、免疫优化算法（文献［2］）和这里方法均在同一环境下搜索和规划路径，将三种不同方法下所产生的规划路径最终结果绘制成图，如图4所示。

图4 三种方法下路径走向曲线图Fig.4 Path Trend Curve under Three Methods

从图4中可以看出利用电势场法所规划的路径相对较为平滑，但不能避免较大的转折点，且路径相对较长，免疫优化算法所规划的路径和这里方法下规划的路径大致相同，不同的是免疫优化算法的路径折点较多且路径更长，这就会使爬壁机器人移动时在耗能以及灵活度上处于劣势，相比之下，这里方法规划的路径在完美躲避障碍物的同时，相对较短且折点较少、更加平滑。

5.3 路径规划收敛性对比

经过路径规划的对比，只能从单一方面看出路径的优劣，但对方法的整体性能并不能作出一个客观的判断，因此为了进一步验证方法的有效性，这里对三种方法收敛情况作出详细对比，绘制成收敛曲线图，如图5所示。从图5中可以看出，与电势场法和免疫优化算法相比，这里方法收敛曲线更为平稳，且能够在较少的迭代次数内进行较大幅度地收敛，相较之下收敛速度更快，稳定性更高，在同样的地图上运动，这里所提方法能够使机器人通过更少次数的迭代运算找到最优路径，效果较好。

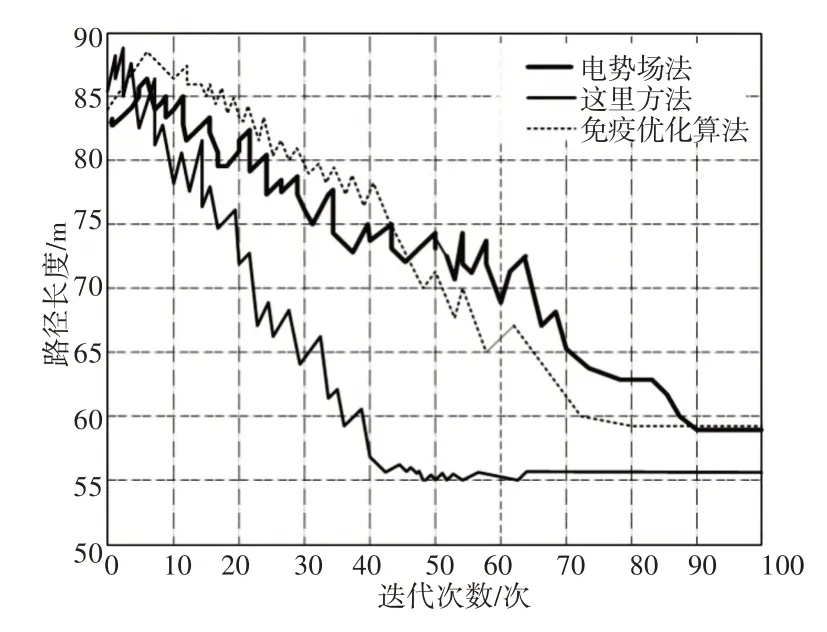
图5 爬壁机器人壁面运动收敛曲线图Fig.5 Convergence Curve of Wall Motion of Wall Climbing Robot

6 结论

为解决爬壁机器人在作业时，面对固定障碍物或是移动障碍物发生接触碰撞问题，这里提出了基于越障步态数据挖掘的路径规划方法。

（1）实验结果表明，所提方法规划路径较短且折点更少，能够在一定程度上减少机器人的耗能，并使路径更加平滑减少机器人在避免移动的困难性，同时算法收敛更快耗时更短，有效提高了路径规划的效率以及机器人的反应能力，且规划误差小，行动轨迹相对稳定，有效性更好，适用性较高。

（2）这里方法同样存在局限性，针对凹型障碍物的避障还须进一步研究。