超薄切割砂轮厚度在线测量方法及误差分析

牛瑞明，朱振伟，赵华东，郑艳萍

（1.郑州大学机械与动力工程学院，河南 郑州 450001；2.河南省智能制造研究院，河南 郑州 450000）

1 引言

在磨具磨料行业，厚度小于1mm的砂轮属于超薄切割砂轮，主要用于光学及电子行业精密元器件的切割加工［1］，这种砂轮厚度的尺寸精度一般要求控制在±2μm之内。目前我国已经能够生产出厚度为（0.1～1）mm的超薄砂轮片，在生产过程中，行业内均采用人工以千分尺为工具进行测量的方法［2］。由于测量人员的工作状态，以及不同测量人员的操作差异，造成测量结果的不确定度区间较大，影响砂轮产品的质量评判，误判率较高。同时，人工测量属于离线滞后测量，不利于实现自动化。并且人工测量结果与砂轮生产过程参数无法实时关联，难以及时对生产起到反馈和调节作用，不利于整个行业智能化升级改造。因此研究在砂轮制造生产线上厚度在线测量，实现生产结果和生产过程的数据关联，对提高砂轮生产过程的检测精度，促进行业的智能化升级有着重要意义。

2 超薄切割砂轮片厚度测量方法的研究及原理介绍

2.1 测量方法的研究

针对厚度检测方案国内外均有相关研究，目前国外的研究方向有聚焦离子束、超声反射等测量方式［3-4］；文献［3］研究了聚焦离子束测量厚度的方式，文献［4］研究了超声反射方式测量厚度的方式。当前国内的研究方向主要是采用激光传感器、基于光反射技术、机器视觉等非接触式的测量方式［5-7］。非接触式测量技术中的激光扫描传感器、机器视觉等新型视觉测量产品以及超声反射和光反射技术，理论上可以一次获得多个方向的曲面测量数据，满足多要素测量的要求，但是其测量精度无法满足一些精度要求较高的测量项目，其信息处理过程可能耗时较长［8］。根据样本测量结果，如图1所示。非接触式测量方法明显比接触式测量方法误差大，因此选用接触式位移测量方法。

图1 接触式和非接触式测量方法的对比Fig.1 Comparison of Contact and Non-Contact Measurement Methods

在确定接触式测量方式的基础上，单传感器测量与多传感器测量成为影响测量精度的主要原因。基于传感器检测方式的广泛应用，研究者们开发了多传感器测量系统，集成多个或多类传感器进行组合测量已经成为工业检测的重要发展趋势［9-10］。单一位移传感器虽然测量精度高、速度快，但测量基准要求太高，在测量复杂零件时需要大量的传感器配合实现［11-14］。单一传感器测量与对顶式传感器测量方法比较，如图2所示。单一传感器测量需要旋转台旋转时有较高的精度，并且测量时容易造成砂轮片表面划伤；而对顶式测量方式不需要旋转台有较高的精度，并且不会使砂轮片表面划伤，而且误差波动相对平稳，因此本设计方案采用位移传感器对顶的测量方式，间接的得到超薄切割砂轮片厚度的测量方式。

图2 单一传感器测量和对顶式测量数据对比Fig.2 Comparison of Single Sensor Measurement and Counter Top Measurement Data

2.2 厚度测量原理

本设计方案采用两个位移传感器对顶的测量方式，通过气压使得传感器测量头伸出，然后计算出超薄切割砂轮片厚度。首先固定两传感器的位置，两传感器测头伸出确定L0的长度；然后根据传感器的位置分别得到上传感器到达超薄切割砂轮片的距离L1，下传感器到达超薄切割砂轮片的距离L2，先假设其距离相等。在测量超薄切割砂轮片厚度之前首先根据其基准厚度选择测量时的气压。在气压一定时，已知接触式传感器标定距离为L0和两个接触式传感器探头移动的距离，计算超薄切割砂轮片的厚度δ=L0-L1-L2。厚度测量原理，如图3所示。

图3 传感器对顶测量原理图Fig.3 Schematic Diagram of Sensor to Top Measurement

3 气压对薄切割砂轮片厚度测量精度的影响

在超薄切割砂轮片测量时，由于传感器是气压传感器，因此气压大小影响了测量的精度。当气压过大时，由于超薄切割砂轮片的变形会导致测量数据比实际尺寸要小；气压过小时，由于薄切割砂轮片在磨削过程中产生的翘曲变形会导致测量数值偏大［15］。同时在测量超薄切割砂轮片厚度时，传感器在测量超薄切割砂轮片时的位置是随机的，因此要控制传感器的气压，使传感器测量头所测位置无论是否发生翘曲变形均能测出超薄切割砂轮片的真实值。

3.1 翘曲变形对气压大小的影响

当超薄切割砂轮片发生翘曲变形时，测量值会偏大，为了测量值相对准确，需要传感器增加输出载荷。根据广义胡克定理可得变形量与载荷之间的关系：

式中：Δδ—翘曲变形量；δ—超薄切割砂轮片的厚度；A—超薄切割砂轮片与传感器测量头的接触面积；F—传感器输出载荷；E—超薄切割砂轮片的杨氏弹性模量。

由于传感器是以气压为动力，根据气压基础公式F=PS，在气压通过气管进入传感器时，气压在管道内会有所损耗，设损耗因子为α（0 ＜α≤1），此时有气压公式：

式中：F1—气压对传感器的载荷；

P—耗损前的气压；

S—传感器内部气道的面积；

α—气压在气道中的损失因子。

传感器内部的阻力是由传感器复位功能导致的。在测量头伸出时，在弹簧的作用下有一个与测量头伸出方向相反的力，其弹簧的力学模型：

式中：k—传感器内部的弹簧系数；

x—传感器测量头伸出的长度；

F2—传感器内部的阻力。

传感器的输出载荷与传感器内部阻力之间的关系：

把式（1）、式（3）、式（4）代入到式（2）中可以得到超薄切割砂轮片在翘曲时的气压：

3.2 平面变形对气压大小的影响

当超薄切割砂轮片没有变形时，传感器输出的载荷作用在砂轮片上时，会导致砂轮片变形，根据平面的应力应变的边界条件：

式中：εx—传感器压砂轮片时的变形量。

把式（2）～式（4）带入式（6）中有：

由于测量的误差范围是±2μm，因此超薄切割砂轮平面的变形量εmax≤2μm，即测量时的气压

4 机构对测量误差影响分析

在超薄切割砂轮片厚度测量时，超薄切割砂轮片与传感器接触的点称为测点；超薄切割砂轮片与旋转台接触的点称为支撑点。由于测点与支撑点不在同一水平面上，假设下传感器会把超薄切割砂轮片顶起，高度为h1；超薄切割砂轮片与旋转台之间会产生一个夹角，这里用θ表示；两传感器之间的距离即为超薄切割砂轮厚度测量值δ1；传感器与超薄切割砂轮片外径的距离为a；传感器测量头的直径用D1表示；测点处传感器与超薄切割砂轮片的距离为h；超薄切割砂轮片厚度δ。当气压一定时，超薄切割砂轮片的厚度与传感器测量头的夹角是影响测量的主要因素。假设超薄切割砂轮片是刚性体，建立数学模型得到测量误差。超薄切割砂轮片厚度测量误差示意图，如图4所示。

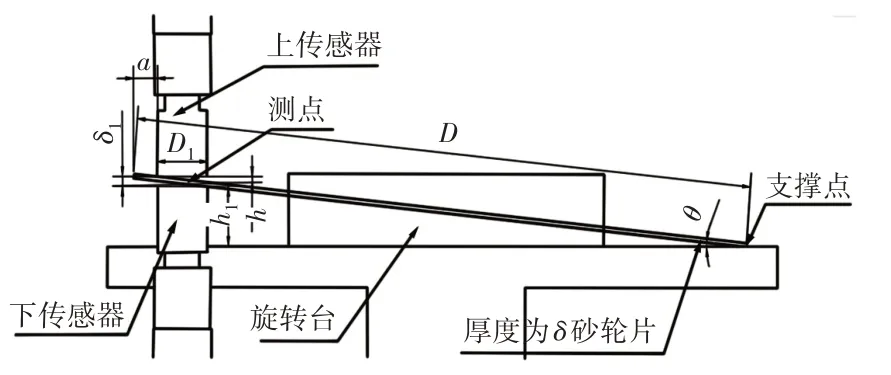
图4 机构对测量误差影响示意图Fig.4 Schematic Diagram of the Influence of Mechanism on Measurement Error

根据图示关系，建立关于超薄切割砂轮片直径D、超薄切割砂轮片厚度δ、两传感器之间的距离为δ1、误差值∊、夹角θ之间的数学模型：

将式（8）代入式（9）得到测量值：

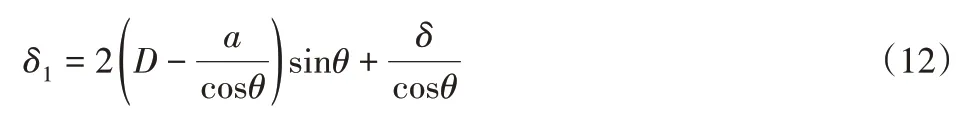
在行业内，常见的超薄切割砂轮片直径D的取值范围在（56～78）mm之内［1］。

利用MATLAB对上述数学模型进行求解，当直径D一定时，厚度测量值δ1随着夹角θ的增加而变大；当夹角θ一定时，厚度测量值δ1随着直径D的增加而变大。根据式（11）可知，超薄切割砂轮片的厚度值δ与超薄切割砂轮片厚度测量值δ1之间的关系：当夹角θ增大时，δ1与δ的差越大，即测量误差∊越大。然后将计算的误差值∊补偿到测量值δ1中，此时δ1与δ的差才是实际的误差。根据式（11）得出在不同厚度值δ和直径D下的误差值，如表1所示。

表1 计算所得误差∊（mm）Tab.1 The Calculated Error is ∊（mm）

5 实验数据验证

通过以上模型的建立与求解分析，传感器对顶式测量超薄切割砂轮厚度的方案理论上是可行的，但需要实验，并通过分析大量的实验数据进行验证。实验装置，如图5所示。

图5 超薄切割砂轮厚度实验装置Fig.5 Experimental Device for the Thickness of Ultra-Thin Cutting Grinding Wheel

根据表2计算的误差补偿到传感器测量值中，然后减去厚度值，得到新的误差。利用图5所示的实验装置对（78×0.3）mm规格的超薄切割砂轮片进行反复测量，将误差数据绘制成折线图，如图6所示。

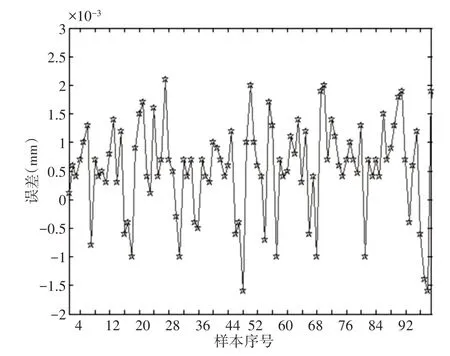
图6 实测误差折线图Fig.6 Line Graph of Measured Error

经过大量的实验结果比对显示误差稳定在-0.0016mm ≤ω≤0.0021mm范围内，与实际要求的误差范围有一定的偏差，但实验测得的误差范围比要求的范围要小。通过分析，由于在实际测量过程中，整个测量系统通过补偿计算误差使得实际的测量误差范围小。与人工测量时超薄切割砂轮片的合格率对比，厚度在线检测设备合格率高达98%以上，符合能够满足实际工程需要。

6 结论

通过比较测量方式，发现接触式测量的误差比非接触式测量的误差小；单一传感器测量比对顶式测量的误差小，但由于旋转台旋转时的精度问题而造成测量误差不稳定，所以选择对顶式位移测量方式。对超薄切割砂轮片进行受力分析时发现不同厚度的超薄切割砂轮片所需要的气压是不同的；在假设超薄切割砂轮片处于最大局部变形时，且测量误差在要求范围内，通过测试计算所得的气压是合适的。通过MATLAB计算及实验数据验证分析，实验测得的误差最大值比要求误差要大，但实验测得的误差范围比要求的误差范围要小，符合工程实际。