螺旋桨铣磨机器人动态特性及振动抑制研究
丁文政,贺文权,陈浩文,陈生华
(1.南京工程学院先进数控技术江苏省高校重点实验室,江苏 南京 211167;2.南京高精船用设备有限公司,江苏 南京 211003)
1 引言
大型船用螺旋桨叶,直径6m以上,传统数控机床很难满足叶片铣磨加工空间的要求,而工业机器人工作空间范围大,在大型零件的加工中有优势,尤其是6-DOF的机器人契合叶片复杂型面的加工需求[1]。但不足是工业机器人刚性没有数控机床高,尤其是螺旋桨铣磨加工用大型工业机器人,其负载在100kg以上,自重负载比仅在5左右,刚体动力学分析已不能满足铣磨精度的要求。大负载的特性使得机器人机械臂的刚性远大于转动轴的刚度,柔性主要集中在关节处,关节柔性将导致机器人在高速加工中产生振动[2]。因而准确的动力学分析是掌握螺旋桨铣磨机器人动态特性,进行振动抑制的基础。
国内外学者在这方面已经开展了相关研究。文献[3]对单机械臂进行了刚体动力学和逆动力学建模,但没有考虑关节柔性影响。文献[4]针对小型仿人手臂的3-DOF机械臂,建立了刚柔耦合的动力学模型,通过有限段法分析不同边界条件下的柔性臂模态。文献[5]针对4-DOF的码垛机器人进行了柔性动力学建模和仿真,但缺乏试验验证。文献[6]基于拉格朗日法建立了太空环境下,柔性机械臂的动力学方程,并且基于假设模态法对动力学方程进行了离散求解。文献[7]基于Hamilton原理建立了柔性机械臂和柔性关节相结合的动力学方程,并利用假设模态法分析了机械臂在外力作用下的动力学响应特性。但上述研究都没有涉及刚性臂和柔性关节相结合的6-DOF大型螺旋桨铣磨机器人的动力学和振动分析。这里以大型船用螺旋桨铣磨机器人为研究对象,建立包含关节柔性的机器人动力学模型,依据CAD数据和实验辨识得到模型中各参数;通过动态响应仿真和振动测试试验分析机器人各关节的动态特性;在此基础上研究基于简单可行的PID算法进行关节振动抑制。
2 包含关节柔性的机器人动力学建模
螺旋桨铣磨机器人的6 根刚性臂由6 台电机通过6 个柔性转动关节驱动。这里柔性关节具有小弹性变形特性,按照文献[8]的假设,将柔性关节的弹性变形近似为刚度系数为K的线性扭转弹簧,通过线性扭转弹簧将电机转子和刚性臂杆相连,其结构,如图1所示。

图1 柔性关节模型Fig.1 Model of Flexible Joint
图中:qi—第i个关节处的刚性臂杆的位置;θi—第i个关节处电机转子通过减速器输出的位置;Ki—柔性关节近似成的线性扭转弹簧的刚度系数;τi—i个关节处施加到刚性臂杆上的力矩。整个螺旋桨铣磨机器人的动力学方程如下:

式中:D(q)—6×6阶刚性臂杆转动惯量矩阵;C(q,)—6×6阶科氏力矩阵;G(q)—6×1阶重力列向量;K—6×6阶关节柔性刚度对称矩阵,即线性扭转弹簧系数矩阵;J—6×6阶电机转动惯量对称矩阵;τ—6×1阶施加到刚性臂杆的力矩列向量。
在上述理论分析的基础上,在Matlab 的SimMechanics 工具箱中建立包含关节柔性的6-DOF 螺旋桨铣磨机器人动力学模型。其中机械结构参数由机器人CAD 模型计算得到,如表1 所示;各关节刚度通过文献[9]的辨识实验法得到,同时利用系统对给定阶跃输入信号开环响应的辨识实验得到各关节处的等效阻尼,刚度与阻尼参数,如表2 所示。机器人各轴运动参数,如表3所示。

表1 螺旋桨铣磨机器人各臂杆参数表Tab.1 Parameters of Links in Propeller Milling and Grinding Robot

表2 螺旋桨铣磨机器人各关节参数表Tab.2 Parameters of Joints in Propeller Milling and Grinding Robot

表3 螺旋桨铣磨机器人各轴运动参数表Tab.3 Parameters of Axes in Propeller Milling and Grinding Robot
3 振动试验与动态响应仿真比较
为了验证上述包含关节柔性的动力学模型,在6-DOF螺旋桨铣磨机器人上进行振动测试试验,并与模型的动态响应仿真比较。试验平台,如图2 所示。主要包括PC 主机、6-DOF 螺旋桨铣磨机器人、动态信号分析仪以及加速度传感器等组成。PC主机上装有DASP 动态信号采集与分析软件,通过该软件设置分析仪的采样频率与时间,将加速度传感器分别与分析仪的六路通道和机器人各个关节相连接,测量机器人运行过程中各关节产生的振动信号。

图2 螺旋桨铣磨机器人振动测试试验平台Fig.2 Vibration Test Platform for Propeller Milling and Grinding Robot
试验中,设定机器人末端执行器的轨迹为一矩形工作空间,加速段的加速度设为7.22rad/s2,减速段的加速度设为7.34rad/s2,最大运动速度为2.59rad/s,正常运动速度为中速。由加速度传感器采集到的机器人运行中各关节振动位移曲线,如图3所示。
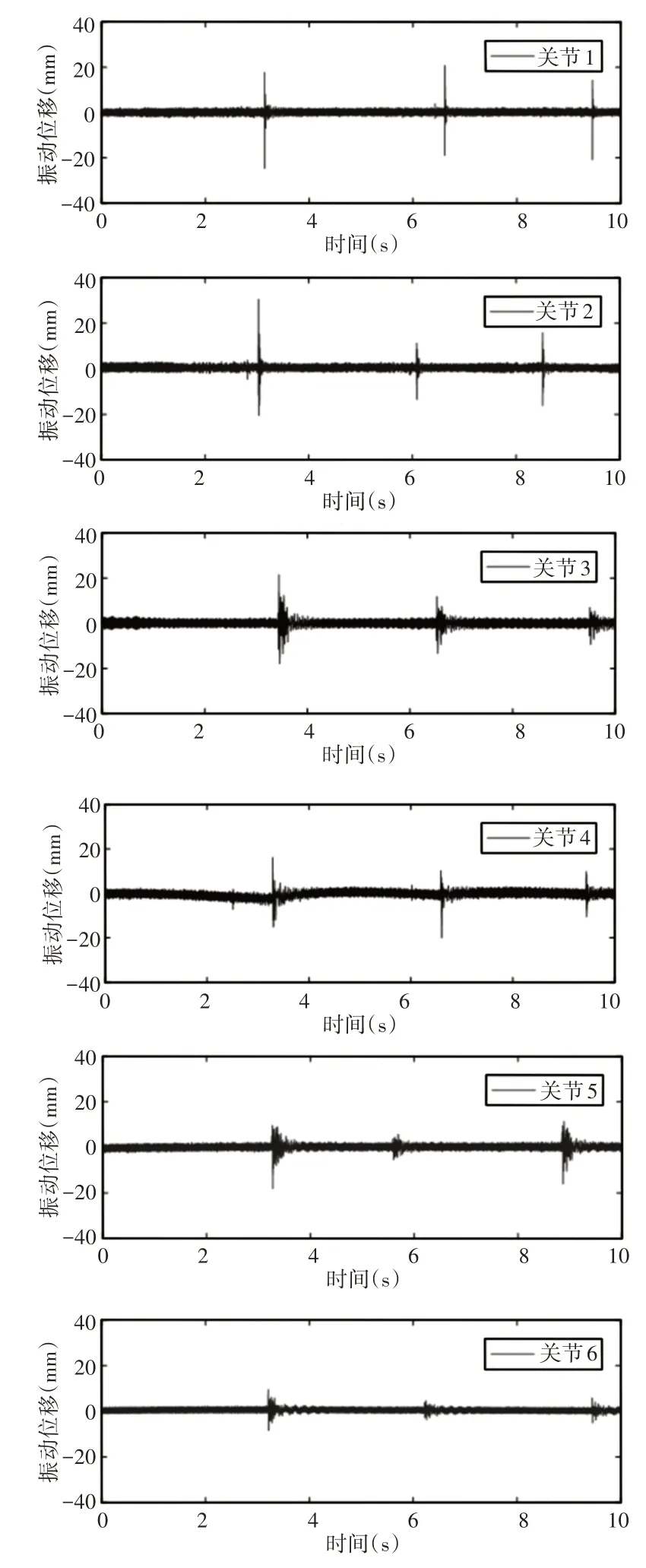
图3 各关节振动位移Fig.3 Vibration Displacements of Joints
从图中可以看出,螺旋桨铣磨机器人各关节在2.5s 左右时开始产生振动,即在矩形运动轨迹的拐点处,此时系统处于加减速阶段,在惯性力的作用下,由于关节柔性产生了振动,最大振动位移在关节1处,达到20mm左右;当速度稳定后,振动位移变小,到达下一个拐点处,再次产生明显的振动。对上节建立的包含关节柔性的动力学模型进行动态响应仿真,截取其中部分测试值与仿真数据比较结果,如图4所示。可以看出,六个关节的仿真结果与试验测试值基本一致,由于试验中螺旋桨铣磨机器人在运行中存在外部环境因素的干扰,即使在静止状态下,自身也存在微小的抖动,而仿真中为理想状态,所以静止后,振动消减为零。另外由于6-DOF 机器人的机械臂之间存在耦合作用,因此关节1处的振动位移相对于关节6处要大得多,试验测试结果也显示前两个关节处的振动尤为明显。表明这里建立的动力学模型符合螺旋桨铣磨机器人的动态特性,为接下来的振动抑制奠定了基础。

图4 各关节振动试验与仿真比较Fig.4 Vibration Comparison of Joints between Test and Simulation
4 基于PID控制的关节振动抑制
关于机器人的关节振动抑制,出现了滑模控制、内模控制和陷波滤波器等多种算法[10],但这些算法与工程上机器人关节伺服系统的控制结构完全不同,在实际中很难推广应用。而PID控制是工业上使用最广泛的控制方法,结构简单,商用伺服控制系统中都有,是工程中最可行的振动抑制控制方法,只是参数的整定需要通过调试确定。
考虑到螺旋桨铣磨机器人在关节1和关节2处的振动幅值最大,在Simulink中分别建立轴1和轴2的伺服系统,如图5所示。并驱动SimMechanics中的包含关节柔性的螺旋桨铣磨机器人动力学模型。其中,ωref是输入参考速度,rad/s;ω0是电动机输出角速度,rad/s;Kvp是速度环增益,A·s/rad;Kcp是电流环增益,A/V;Ke是电动机反电动势常数,V·s/rad;Lq是电动机q轴等效电感,H;Rq是电动机q轴等效电阻,Ω;Kf是电磁转矩常数,N·m/A;T0是输出驱动转矩,N·m;TF是负载转矩,N·m。

图5 单轴伺服驱动系统Fig.5 Servo Driving System of a Single Axis
在Matlab中首先用继电反馈算法进行参数自整定,然后进行适当调节,得到两轴的控制参数如下。轴1的PID控制参数:KP=200,KI=260,KD=260;轴2的PID 控制参数:KP=30,KI=80,KD=55;并将该参数输入机器人控制器中,再次进行运行过程的振动测试试验结果,如图6所示。从图中可看出,关节1与关节2的振动位移都能够在0.2s左右减小为零,且最大振动位移仅为未加控制时的1/3,可见,通过经典PID控制算法能够有效抑制螺旋桨铣磨机器人由于关节柔性产生的振动。

图6 振动抑制结果Fig.6 Results of Vibration Suppression
5 结论
(1)针对大型螺旋桨铣磨机器人柔性主要集中在关节处的特点,建立了刚性臂和柔性关节相结合的6-DOF动力学模型,为铣磨机器人的动态特性研究提供了依据。(2)通过动态响应仿真和振动测试试验分析了关节柔性对机器人各关节动态特性的影响,结果为有效抑制螺旋桨铣磨机器人运行过程中的振动奠定了基础。(3)研究通过工程上简单可行的PID算法进行振动抑制,试验结果表明在Matlab中基于这里建立的动力学模型整定的PID参数有效抑制了机器人运行中振幅最大两处关节的振动。

