Yield enhancement of elliptical high harmonics driven by bicircular laser pulses

Xiaofan Zhang(张晓凡) and Xiaosong Zhu(祝晓松)

1Hubei Key Laboratory of Optical Information and Pattern Recognition,Wuhan Institute of Technology,Wuhan 430205,China

2Wuhan National Laboratory for Optoelectronics and School of Physics,Huazhong University of Science and Technology,Wuhan 430074,China

We theoretically investigate the yield enhancement of elliptical high harmonics in the interaction of molecules with bicircular laser pulses by solving the time-dependent Schr¨odinger equation. It is shown that by adjusting the relative intensity ratio of the two bicircular field components in specific ranges the yield of the molecular high harmonics for the plateau and cutoff regions can be respectively enhanced. To analyze this enhancement phenomenon, we calculate the weights of the electron classical trajectories. Additionally, we also study the ellipticity distribution of harmonics for different intensity ratios. We find that these enhanced harmonics are elliptically polarized, which we mainly attribute to the recombination dipole moment of the major weighted trajectories. These enhanced elliptical extreme ultraviolet and soft x-ray radiations may serve as essential tools for exploring the ultrafast dynamics in magnetic materials and chiral media.

Keywords: high harmonics,extreme ultraviolet and soft x-ray,bicircular laser pulses

1. Introduction

High harmonic generation (HHG) is a highly nonlinear phenomenon occurring when targets are irradiated by strong laser fields.[1]The generation process can be understood by the classical three-step model.[2]First, electrons are ionized from the nucleus and into the continuum. Second, under the influence of the driving field, the electrons are accelerated.Third, the accelerated electrons are driven back to the parent nucleus and liberate their accumulated kinetic energy,i.e.,HHG occurs. HHG is an indispensable way to generate extreme ultraviolet (XUV) radiation and soft x-rays.[3]A number of studies have shed light on numerous scientific areas such as atomic and molecular physics, solid physics, chemistry,etc.[4–9]Motivated by the abundant applications,the generation of XUV and soft x-ray radiation has attracted much interest. Compared with the other major method of producing XUV and soft x-ray radiation by synchrotrons or free-electron lasers (FELs),[10–12]which requires large-scale x-ray facilities, radiation based on HHG can be realized on a table-top scale.[13–17]The pulse duration of these radiations can be in the attosecond (as) range. Since this timescale is the same as the natural time of electrons in atoms and molecules, it is possible for attosecond pulses to detect the electron dynamics in matter. Compared with linear pulses, elliptical attosecond pulses possess an additional degree of freedom,which enlarges the range of applications. For example,elliptically polarized attosecond pulses can be applied to study the ultrafast chiral-specific dynamics in molecules and x-ray magnetic circular dichroism spectroscopy.[16–18]Hence, the generation of elliptical attosecond pulses has been the focus of many theoretical and experimental studies. On the basis of the macroscopic and microscopic character of the HHG process, several methods have been proposed in past few years. Macroscopically,noncollinear driving laser fields have been adopted to produce elliptically polarized high-order harmonics.[19–21]Microscopically, one can prepare the specified targets to obtain elliptical harmonics,[22–25]for example preparing ringcurrent states with a large angular momentum[22,23]or prealigning molecules.[25]Alternatively, one can also apply a two-dimensional (2D) synthesized driving field, for example applying few-cycle elliptical pulses combined with a terahertz field[26]or orthogonal two-color fields.[17,27]However, some drawbacks were still found in the above approaches,[20,27]such as the small ellipticity or low yield of the attosecond pulses and relatively complex optical set-up requirements.

Recently, another 2D synthesized driving field, i.e., the bicircular laser field (BLF), has attracted a great deal of attention[28–39]due to two features of the harmonics generated by this field. One is that the conversion efficiency of HHG does not need to be compromised. The other is that the high harmonics are circularly polarized. A BLF consists of two coplanar counter-rotating circularly polarized laser fields.These two components possess frequenciesωand 2ω. The time-dependent electric field has three-fold symmetry on its polarization plane. Because of the special symmetry of the interaction systems,each harmonic is circularly polarized and the adjacent harmonics possess opposite helicities.Given that,the attosecond pulses synthesized by these harmonics are almost linearly polarized. In order to generate elliptically polarized attosecond pulses by the BLF scheme,one can break the symmetry of the interaction systems. For example, one can prepare the molecules as the targets of interaction[35,37,38]and adjust the two BLF components.[39,40]In order to accurately control the yield and polarization of HHG,the correspondence between harmonics and electron trajectories in the interaction of molecules and BLFs with different intensity ratios needs to be established.

In our study,we investigate the yield and polarization of molecular high harmonics generated by a BLF with different intensity ratios between its twoωand 2ωcomponents. Based on the results obtained by solving the 2D time-dependent Schr¨odinger equation (TDSE), we find that the yield of high harmonics in the plateau and cutoff regions can be respectively enhanced by adjusting the intensity ratio of BLFs in specific ranges.In order to interpret these phenomena,we calculate the weight of the electron classical trajectories.These classical results can intuitively interpret the enhancement of harmonics.Additionally, we also investigate the ellipticity of harmonics when adjusting the intensity ratio of BLFs. Our results indicate that the enhanced harmonics are elliptically polarized and the ellipticity is not smaller than that of harmonics by the usual BLFs with two equal intensity components. Then, we calculate the ellipticity of the recombination dipole moment and the results indicate that the ellipticity of the enhanced high harmonics mainly depends on the recombination dipole moment of the major weighted trajectories. Our work provides a clear physical picture of the yield enhancement of the elliptical high harmonic when adjusting the intensity ratio of the BLFs.

2. Theoretical model

The high harmonics by the BLFs are calculated by numerically solving the 2D TDSE in length gauge,which can be written as (atomic units (a.u.) are used throughout this paper unless otherwise stated)[41]in whichξ= 0.5 andρ= 1.746 are the softening and the screening parameters. Following Ref.[41],we use the parameters ofZ1i=6,Z2i=4,Z1o=0.6,andZ2o=0.4.rj=r-Rjwithr ≡(x,y),R1≡(x1,y1)andR2≡(x2,y2)being the positions of the electrons, O nuclei and C nuclei. Here,x1/2=±R1/2cosθ,y1/2=±R1/2sinθ,R1=R/(1+β), andR2=βR/(1+β)withβ=Z1i/Z2i=Z1o/Z2o=1.5.R=2.13 a.u.is the internuclear separation.θis the alignment angle of the molecular axis relative to thexaxis. Here, we assume thatθ=0,i.e.,the molecular axis is aligned along thexaxis. It is worth noting that the polar molecules are applied rather than the nonpolar molecules. This is because the polar molecules can contribute to the large ellipticity of harmonics. This statement can be verified by the recombination dipole moment.With the plane-wave approximation,the recombination dipole moment can be written asd(p;θ)=〈ψ0(θ)|r|exp(ip·r)〉,in whichψ0andpare the ground state and the recombination momentum.[44,45]For nonpolar molecules, such as N2molecules, their ground states are symmetric and satisfy the conditionψ0(x,y,z;θ)=ψ0(-x,-y,z;θ). But, the nonsymmetric ground state of polar molecule CO does not satisfy this condition. Then, the real and imaginary parts of the recombination dipole moment are Re[di] = 0 and Im[di]/= 0 for N2, and Re[di]/=0 and Im[di]/=0 (i=x,y) for CO. Given that, the relative phase betweendxanddyis only 0 and±πfor N2, which results in the linearly polarized high harmonics. However, for CO, the relative phase can be other values including the±π/2,which results in the elliptically polarized high harmonics. Therefore,in our study,we choose the polar molecule CO as the target to investigate the enhancement of the elliptical harmonics by BLFs. The ground stateψ0of the target molecule is obtained by solving TDSE with imaginary time propagation. In our calculation,the wave function is discretized on a 2D grid which ranges from 240 a.u.to-240 a.u.The space step size of the grid is Δx= Δy= 0.1172 a.u.The time step size for the evolution of the wave function is Δt=0.1077 a.u.E(t)in Eq.(2)is the driving field,i.e.,BLF.It is obtained by combing two components, left- and rightcircularly polarized laser pulses. The laser vector in thex–ypolarized plane is

3. Results and discussion

First, we calculate the harmonic spectra from CO molecules driven by BLFs with different intensity ratios of the two components. The harmonic intensity distribution is presented in Fig.1(a). We divide this result into two regions for analysis. For the region ofr ＞2, one can see that the yield of high harmonics in the cutoff region is enhanced. When the ratio keeps increasing and exceeds 6,the yield of the total harmonic spectrum decreases. For the region ofr ＜2, the yield of high harmonics in the plateau region is higher than that in the cutoff region. Besides, it increases with increasing ofrin the range of 0 to 2. Especially, the harmonic intensity forr=2 (labeled by the red dashed line) is higher than that forr=1(labeled by the blue dashed line),which is the case that has been studied in most works.[28–35]To clearly exhibit the yield enhancement of high harmonics, we plot the high harmonic spectra as a function of harmonic orders forr=1(blue line),r=2 (red line), andr=3.2 (green line) in Fig. 1(b).The corresponding BLFs are plotted in the insets respectively,of which the BLF forr=1 is the usual case. From Fig.1(b),one can see that the yield of harmonics at the cutoff region forr=3.2 is higher than that in the plateau region. Whereas,forr=1 andr=2,the yield of harmonics at the plateau region is higher than that in the cutoff region.

Fig.1. High harmonic spectra from a CO molecule. (a)Intensity distribution of high harmonics versus harmonic order and intensity ratio r between the two bicircular field components. The blue,red and green dashed lines represent the harmonic spectra with r=1, 2, and 3.2. (b) Harmonic intensity as a function of the harmonic order with intensity ratio r=1(blue line),r=2(red line),and r=3.2(green line).The insets show the bicircular laser pulses with r=1,2,and 3.2.

Fig. 2. (a) Weight distributions of classical trajectories of electrons versus the intensity ratio r and the recombination time. (b)The classical recombination trajectories in the bicircular laser pulses with r=1(green star markers)and r =2 (orange star markers). For clarity, we only present the electron trajectories with the ionization time less than T0/3.

In order to interpret the yield enhancement of harmonics,we calculate the weight of the classical trajectories of electrons based on the classical three-step model. The weight of the recombination trajectories can be determined by the tunneling theory[48–50]

whereW0(t0) is the tunneling rate of the molecules in the quasi-static approximation andIp=0.529 a.u. is the ionization potential of CO molecules. The weight distribution versus intensity ratiorand recombination time of electrons is presented in Fig. 2(a). For a better comparison with the harmonics,we also plot the recombination energy of electrons as a function of recombination time forr=1 (green star markers) andr=2 (orange star markers) in Fig. 2(b). Due to the three-fold symmetry of the BLFs, there are three ionization and recombination peaks in one optical cycleT0. Thus, several electron trajectories stacked together make the result look more complicated. For clarity and to avoid confusion,we only present the electron trajectories with the ionization time less thanT0/3 in Fig. 2(b). For other values ofr, the recombination times of each peak are almost the same. So,in Fig.2(b),we only present the results ofr=1 and 2 as examples to carry out our discussions. From the figures,one can see that,whenr ＞2,the weight of trajectories in the region between the two red solid lines is greater than that in other regions. Comparing the Figs. 2(a) and 2(b), we find that the electron in this region mainly contributes to the harmonics in the cutoff region. So,the yield of harmonics in the cutoff region is higher than that in the plateau region,which is consistent with the results in Fig. 1(a). If the intensity ratio keeps increasing, the weight of all trajectories is low. Correspondingly,the yield of harmonics no matter in the cut-off region or plateau region decreases. This can be understood by an intuitive interpretation picture. Since the driving field with a larger intensity ratioris close to the circularly polarized pulses, the recombination probability of electrons is small and thus the yield of the total harmonic spectrum is low,which is also consistent with the results in Fig.1(a). If the intensity ratio is in the range ofr ＜2,one can see that the major weighted recombination trajectories contribute to the harmonics in the plateau region. So,the yield of harmonics in the plateau region is larger than that in the cutoff region. Besides,with increasingrin this range,the weight of the recombination trajectories increases.This is also consistent with the results in Fig. 1. Therefore, the yield enhancement of high harmonics by adjusting the intensity ratio of BLFs has been clearly interpreted by the classical electron trajectories.

Then,we also investigate the influence of the intensity ratioron the ellipticity of high harmonics. The result is plotted in Fig.3(a). One can see from this figure that,for the intensity ratior ＞2,the ellipticity of the harmonics in the cut-off region is purely negative.That is to say,the attosecond pulses synthesized by these harmonics are absolutely elliptically polarized and the polarization direction is counterclockwise, which is the same as that of the second-harmonic component 2ωfield.However, in the plateau region, the clockwise and counterclockwise harmonics are mixed together , which will reduce the ellipticity of the attosecond pulses synthesized by these harmonics and cannot even promise the elliptical attosecond pulse generation. For the intensity ratior ＜2, the ellipticity of the harmonics in the plateau regions is purely negative.The same sign of the harmonic ellipticity will not reduce the ellipticity of the synthesized attosecond pulses. Therefore,according to the results in Fig.1,we conclude that the enhanced harmonics are elliptically polarized. Now, we focus on the ellipticity of the attosecond pulses synthesized by these enhanced harmonics . The electric field of the radiation in the temporal domain is obtained by synthesizing the high harmonics in the spectrum range of [75th, 90th]. We present the results forr=1,2,and 3.2 respectively in Figs.3(b)–3(d). One can see that the synthesized attosecond pulses are elliptically polarized.Additionally,we also find that the ellipticities of the attosecond pulses for BLFs withr=2 and 3.2 are larger than that for the usual BLFs withr=1. Therefore,according to the results in Figs. 1 and 3, one can adjust the intensity ratio of BLF to obtain an elliptically polarized attosecond pulse with high yield.

Fig. 3. (a) Ellipticity distribution of high harmonics versus harmonic order and intensity ratio r. (b)–(d) Electronic feild of the synthesized attosecond pulses onto the Ex–Ey plane with r=1,2,and 3.2. The attosecond pulses are synthesized by high harmonics from 75th-order to 90th-order. The ellipticity ε is presented correspondingly.

Finally,we give a classical explanation of the dependence of the harmonic ellipticity distribution on the intensity ratior.We first explore the classical behavior of the electron trajectories. According to the three-step model, we calculate the weight of trajectories as functions of intensity ratiorand recombination angleφof the electrons. The result is presented in Fig. 4(a). From this figure, one can see that, whenr ＜2,most electrons only recombine with the parent nucleus in the angle range of[-45°,-10°].Comparing with Fig.2,we know that these electrons contribute to the harmonics in the plateau region. Whenr ＞2,most electrons still recombine in the angle range of [-45°,-10°]. However, these electrons mainly contribute to the harmonics in the cutoff region. A few electrons recombine with other angle ranges, such as [45°,65°]and [-55°,-45°]. These electrons contribute to the harmonics in the plateau region. In order to analyze the physical reason that the enhanced harmonics are elliptically polarized,we calculate the ellipticity of the recombination dipole moment as functions ofφand harmonic order, which is presented in Fig. 4(b). The ellipticities of the recombination dipole moment withφ=-45°and-10°are labeled by green and magenta dashed lines. From Fig. 4(b), one can see that, in the ranges of [-45°,-10°] and [-55°,-45°], the ellipticity of the recombination dipole moment is negative. In the range of[45°,65°], the ellipticity of the recombination dipole moment is positive. Based on the discussions about Figs. 2 and 4(a),whenr ＜2, the ellipticity of the recombination dipole moment in the plateau region is purely negative. Whenr ＞2,the negative and positive ellipticities of the recombination dipole moment in the plateau region are mixed. Whereas, the ellipticity of the recombination dipole moment in the cutoff region is only negative. These are consistent with the ellipticity distributions of harmonics in Fig. 3(a). From Fig. 4(a), we also find that, when the intensity ratio isr ＜2, the recombination angle is mainly atφ=-35°. Then, we plot the ellipticity of the recombination dipole moment versus harmonic order for the case ofφ=-35°in Fig. 4(c). One can see that the ellipticity of the recombination dipole moment at the harmonic orders[75th,95th]is about-0.162,which is almost consistent with that in Fig.3. Therefore,we classically explained the polarization state of the enhanced harmonics, which is mainly determined by the recombination dipole moment of the major weighted trajectories.

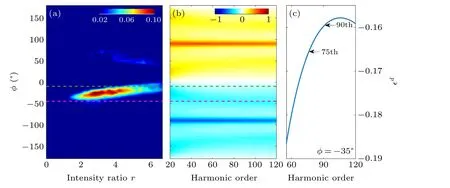
Fig. 4. (a) Weight distributions of classical trajectories of electrons versus intensity ratio r and recombination angle φ between recombination direction and molecular axis in cartesian coordinates. (b)Ellipticity distributions of the recombination dipole moment versus intensity ratio r and recombination angle φ. (c)Ellipticity as a function of harmonic order for φ =-35°.

4. Conclusion

In conclusion, we have theoretically demonstrated that the yield of the molecular high harmonics can be enhanced by adjusting the intensity ratio between the two components of the BLFs. When the intensity ratio is adjusted in different ranges,the yield of harmonics near the cut-off region and in the plateau region can be enhanced respectively. Based on the three-step model,we have given a classical explanation of the enhancement of harmonics by adjusting the intensity ratio of BLFs. Additionally,we have also demonstrated that the attosecond pulses synthesized by these enhanced harmonics are elliptically polarized. We have analyzed the ellipticity of the recombination dipole moment. Our results indicated that the polarization of the enhanced high harmonics is mainly determined by the recombination dipole moment of the major weighted trajectories.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 11904269), the Natural Science Foundation of Hubei Province, China (Grant Nos.2021CFB300 and 2020CFB362),and Scientific Research Program of Hubei Provincial Department of Education(Grant No.B2020176).