Thin-film approximate point scattered function and its application to neutron radiography

Jun Qin • Jia-Yu Ni,2• Lin-Feng Ye,2 • De-Hong Gao,2 • Wei-Jun Jiang

Abstract A simpler and improved utility approximate point scattered function for thin-film converters currently used in neutron photographic devices is proposed as a correction method to produce clearer, more realistic images.The validity of the model was demonstrated through a simulation experiment. Based on the results, an error analysis was carried out, certain corrections were made to the original model,and the final model achieved a very low relative error in the simulation experiment. The model can also be optimized for quantitative neutron photographic analysis using iterative algorithms to obtain realistic neutron photographic images more quickly. At the end of the article,the model is extended to consider the case of energy spectrum hardening by introducing a temperature correction parameter.

Keywords Neutron radiography ∙Point scattered function ∙Image processing

1 Introduction

Neutron radiography is a method for surface or internal diagnosis of a sample to be measured using the properties of neutron attenuation and scattering. Compared to other radiographic techniques, neutrons are more complex because of the manner in which they interact with the nucleus,and the macroscopic cross section does not have a definite relationship with the nuclide species. These properties provide neutron radiography with an unparalleled advantage over other radiographic techniques, such that neutron radiography is currently used in the diagnosis of a wide variety of industrial materials and is of great importance in the metal and aerospace industries [1–3]. Simply put, neutron radiography takes advantage of the transmission of neutrons and the absorption of neutrons by the sample being evaluated, among other properties. By comparing the imaging of the detector in the presence or absence of the sample,the physical condition of the sample can be determined. However, there are inherent errors in this technique, mainly due to the scattering of neutrons by the sample,absorption of neutrons by the detector material,and attenuation of neutrons during transmission. In response to this problem, two main correction methods have been proposed: the first is to modify the energy spectrum of the neutron source to produce more realistic final detection results[4,5],and the second is to introduce various functions to correct for the effect of scattering in neutron radiography [6, 7]. Energy spectrum correction is proposed mainly to counter the neutron energy spectrum hardening problem. This problem becomes more significant as the thickness of the sample to be measured increases to a point at which energy spectrum correction becomes necessary. However, in a broader context, the scattering effect is more direct and important than the energy spectrum hardening effect. Therefore, this paper discusses energy spectrum correction as a secondary correction after scattering correction. For example, the 14 MeV fast neutron radiography (FNR) technique [20],which has been extensively studied in recent years, has promising applications with high contrast sensitivity and other features. However, it has difficulty dealing with the impact of scattering effects, which makes this technique much less effective and restricts its use in practical applications. There are two popular methods for energy spectrum correction: the maximum-likelihood expectationmaximization (MLEM) method and the quantitative neutron photographic analysis (QNPA) method. The MLEM method is mainly based on least squares and maximumlikelihood estimations to perform statistical correction[21],whereas the QNPA method uses the characteristics of neutron decay to perform iterative correction of the neutron distribution in order to correct the energy spectrum.Therefore,this paper discusses energy spectrum correction as a secondary correction after scattering correction, with the optimization of the scattering effect as the primary objective.For the scattering correction,the‘‘point scattered function’’ has been proposed [8]. It is essentially the probabilistic density distribution function of the scattered neutrons detected by the detector after the neutron beam passes through the sample to be measured. However, it is not easy to apply directly because of its complex form and the many parameters it contains. Therefore, scattering correction models based on a variety of approximate pointscattered functions have been proposed [9, 10]. In recent years, materials science has advanced rapidly, and an increasing number of neutron detectors can use very thin detection layers as a converter to optimize neutron radiography[11–13].Thus,we propose a new approximation of the point scattered function called the ‘‘thin-film approximate point scattered function’’. This new model has a significant computational advantage and the error is sufficiently low for practical applications. In the following, we derive the thin-film approximate point scattered function from the conventional point scattered function and then perform numerical simulations using software such as Monte Carlo N-particle transport (MCNP) and Mathematica to evaluate the accuracy of the model and to perform error analysis.

2 Thin-film approximate scattering model

2.1 Thin-film approximate point scattered function

We first review the basic theory of the point scattered function, which is based on four basic assumptions:

1. The scattered neutrons are homogeneous.

2. The neutrons are scattered only once in the sample.

3. The source and scattered neutrons have the same attenuation coefficient in the sample.

4. The sample width is large enough to ensure that the scattered neutrons penetrate the bottom of sample (not the sides) and reach the detector.

These are reasonable assumptions. Because neutrons are electrically neutral, each should be homogeneous after scattering. The vast majority of neutrons also scatter only once in the sample and therefore the need for multiple scattering corrections is not significant.

Figure 1 shows a schematic of neutron radiography and the angular response of the detector.

In Fig. 1,r is the coordinate parameter of the detector,d is the thickness of the detector converter,θ is the scattering angle, D is the distance from the sample to the detector, T is the thickness of the sample, t is the location where scattering occurs in the sample, and R and l are both geometric parameters. The following relationship exists between the geometric parameters.

Then, for the detector coordinate r, the incident neutron flux φsc (E ) and the scattered neutron flux of the detector φst (E ) can be expressed in the following form.

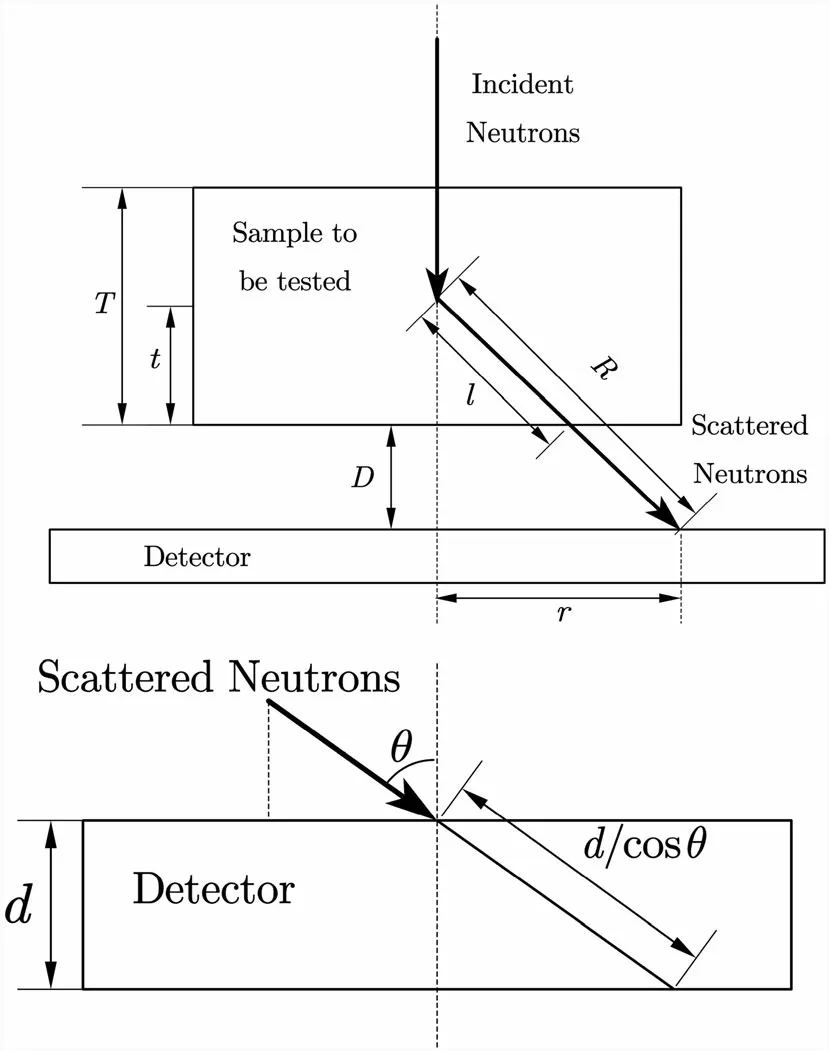
Fig. 1 Schematic diagram of neutron radiography and angular response of the detector

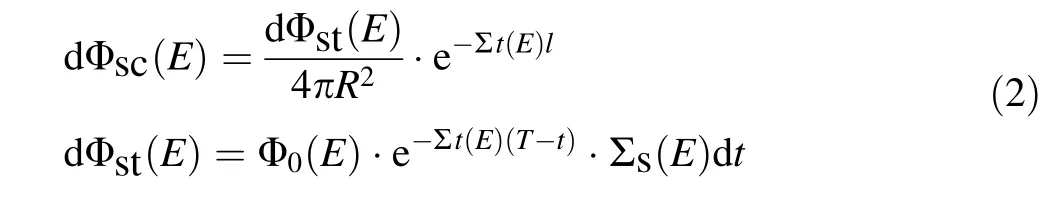
here φ0E( ) is the neutron flux of the source, Σs E( ) and Σt (E ) are the scattering macroscopic cross section and the absorbing macroscopic cross section of the sample,respectively.Σdet (E )is the absorption cross section of the detector material.

We have to take into account the neutron attenuation effect,where a single neutron is detected with a probability of

This function is quite complicated and inconvenient to use.Many studies related to scattering correction have been conducted to approximate this function.

For a very thin detector,it can be considered that d →0.Because the series expansion of the exponential function e-Σd=1-Σd+O [2 ] involves a second-order infinitesimal term O [2 ], we can use this approximation by considering that the main and first-order terms occupy 99%of the exponential function (i.e., d satisfies 1-Σd =0.99e-Σd).This implies that the following approximation can be applied.

Using the geometric relations and the adjustment order,and writing the new function as TPScF(r ), we obtain

This integral can be calculated numerically using the Newton-Cotes method after the associated parameters are given. Finally, the thin-film approximation of the model is

here the integral of E is related to the specific energy spectrum.

2.2 Pre-processing of the model

To better apply this model, we need to pre-process the model, as described in this section. We focus on Eq. (8)and apply the Newton-Cotes method to obtain a numerical solution [14] using

where h represents the step size and m is obtained by solving the following equation.

here [x ]represents the Greatest Integer Function, which returns the value of the greatest integer, which is less than or equal to x. The error that results from Eq. (10) is given by the following equation.

Equation (10) can be calculated very quickly once the determined thickness T of the sample and the absorption cross section Σt (E ) are known.

In addition, the integration of TPScF(r ) is difficult.Therefore, the approach we adopt is to divide the integration interval into many small intervals as follows.

Thus, we consider the model from a numerical perspective, making it less abstract and more computable in concrete terms. Next, we use examples to demonstrate the validity of the model and then perform an error analysis.

3 Application example

3.1 Numerical simulation of scattering correction for water and polyethylene

We construct a simple neutron radiography experiment.The neutron converter is made of 100 μm-thick6Li material, and cylindrical metallic aluminum with a radius of 0.6 cm and a height of 1.1 cm is used as the sample,which is located 0.8 cm away from the detector.The experimental setup is shown in Fig. 2.

As the neutron source in the experiment,we use thermal neutrons ranging in energy from 0.01 to 1 eV and whose energy spectrum satisfies Maxwell’s spectrum.The neutron distribution on the converter can be obtained by importing the relevant parameters into MCNP. The results are represented as density maps for PScF(r ) and TPScF (r ), in Fig. 1.

Fig. 2 Neutron radiography experiment setup

Fig. 3 (Color online) Results of a PScF(r) and b TPScF(r) for the simulation experiment

In the figure, r indicates the distance from the detection point to the center of the detector plane. Figure 3a represents the simulation results using PScF(r ) as a point scattered function, and Fig. 3b represents TPScF(r ) for comparison purposes. The red areas in Fig. 3 indicate heavy neutron scattering, whereas the blue areas indicate very light neutron scattering.The boundary of the red area lies roughly at 0.6 cm, which is generally in line with the actual condition of the sample.Note that the boundaries of the red areas in each figure are not particularly clear. The causes behind this are the idealization of the neutron energy spectrum and the haphazard nature of the scattering in the sample.However,there are well-established methods to solve this problem, mainly by correcting the energy spectrum and by using computer algorithms to make the edges clearer, thus making neutron imaging more representative of the actual experimental conditions [15, 16].Comparing Fig. 3a with b, it can be seen that TPScF(r )gives an overall smaller result than PScF(r ), which indicates that an overall error exists between them. The Relative Error Function is therefore defined as

For the experiment described in Fig. 2, the image of the relative error function is mapped in Fig. 4

This result indicates that the error is very small in the central area of the screen and is larger along the edge areas.The average error over the entire detection screen is approximately 0.306.However,this model is valid because of the similarity between Fig. 3a, b, so, we further review the validity of the model through error analysis below.

3.2 Error analysis

The error function presented in Fig. 4 resembles an exponential function in the radial direction, so we can introduce an exponential function to adjust for the error.First, we define

Fig. 4 (Color online) Results of the relative error distribution between PScF (r ) and TPScF(r )

Then, to study the error relative to the original scattered function, the distribution is plotted in Fig. 5.

The figure indicates that the relative errors are at a very low level in most regions, and a maximum value of 17%and a mean value of 2.5% exist across the entire region.This result indicates that a further improvement can be made to the approximation model, which validates that NPScF(r ) is a very effective point scattered function for the thin-film approximation.

4 Neutron imaging correction

4.1 Quantitative neutron photographic analysis method

Owing to the nature of the interaction between neutrons and matter, the results of neutron imaging are often very inaccurate in actuality. We can reduce the error by using more advanced experimental equipment, and/or we can improve the imaging technique using algorithms to correct an image. One such method, the Quantitative Neutron Photographic Analysis Method uses algorithms to improve imaging technology.

Quantitative neutron photographic analysis uses the exponential neutron decay pattern,

where I is the intensity of the neutron, (i, j) is the prime point in the image, and ΣA is the thickness of the sample.The distribution of substances can be determined using Eq. (17).

Fig.5 (Color online)Relative error distribution between PScF(r )and NPScF(r )

This is the principle behind quantitative neutron photographic analysis method.

Numerous experimental studies have shown that quantitative neutron photographic analysis is influenced by three main factors.

(1) Collimation Ratio

The collimation ratio is the ratio of the distance from the neutron source to the sample with respect to the diameter of the output aperture. Because neutrons are electrically neutral, they cannot be made parallel by focusing the neutron beam through the electromagnetic field, and therefore, it is not possible to achieve full collimation of the neutron beam using a collimator.(2) Scattered Neutrons

The presence of substances with high scattering cross section (e.g., water and polyethylene) in the sample can cause a large number of scattered neutrons to reach the detector, thus distorting and blurring the neutron image.The solution is generally to increase the distance between the sample and the detector.

(3) Neutron Energy Spectrum

Because incident neutrons are not mono-energetic and neutrons having different energies interact with matter having different cross sections, the images and results obtained using a single cross section parameter can produce large errors. In addition, the energy spectrum of the neutrons scattered by the sample may have changed from that of the neutron source owing to attenuation during propagation.

The focus of this study is the correction of neutron images by applying a correction for scattered neutrons. To further investigate the optimization of the proposed model with respect to neutron imaging, the current iterative algorithm for the quantitative analysis of scattered samples is presented in Fig. 7.

In the algorithm,Isuis the normalized neutron intensity,Iscis the scattered neutron distribution function,and k is the number of iterations. The criterion equation

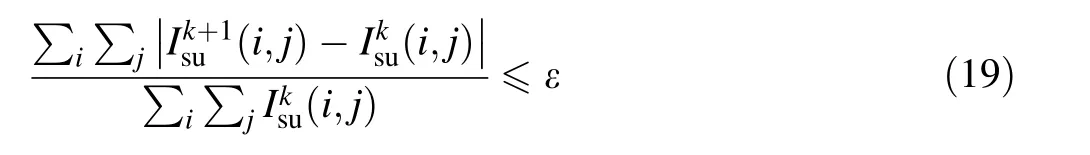
is used to select a convergence coefficient ε that terminates the iterative calculations. The above criterion actually represents the relative change in the transmitted neutron intensity calculated for two adjacent iterations. As the algorithm converges, the value of the change should become increasingly smaller, gradually converging toward zero. This algorithm has been tested in a large number of neutron scattering experiments and is highly reliable. This iterative algorithm can be applied to the thin-film point scattering function model developed above.

4.2 Optimization algorithm based on thin-film approximation models

It should be noted that in the iterative algorithm(Fig. 7),PScF(r )is calculated based on the sample thickness,which is later brought into the calculation of the neutron intensity prior to the iterative calculations. However, if we use NPScF(r ) instead of PScF(r ), the iterative convergence can be greatly accelerated,as NPScF(r )is equivalent to an approximate numerical integration of PScF(r ). When we applied the iterative algorithm to the experiments in Sect. 3.1; using this substitution only three iterations were required to obtain satisfactory results, as indicated in Fig. 6.

Fig. 6 (Color online) Scattering imaging results using (a NPScF(r ),and b PScF r( ))

The results obtained show the reliability and validity of the iterative algorithm on the one hand, and the faster correction of imaging results using NPScF(r ) instead of PScF(r ) on the other. The iterative calculation using PScF(r ) requires five iterations to converge to something closer to actuality and takes approximately three times as long to run as the calculation using NPScF(r ). Comparing result(a)using the NPScF(r )function with result(b)using the conventional PScF(r ), it can be observed that (b) produces poor imaging results, is slower to converge, and exhibits greater distortion at the edges, whereas (a) produces good imaging results and slight distortion at the edges.

We followed up with similar simulations for trapezoidal objects and cones and found that using NPScF (r )instead of PScF(r ) for iterative calculations not only improved the simulation, but also improved the speed of the algorithm.

Moreover, in recent years, a ‘‘3D detector’’ has been introduced for use in neutron photographic techniques[18, 19]. It adds 3D microstructures such as trenches or holes to a planar detector and fills them with a neutron converter, which can significantly improve the detection efficiency. For this class of detectors, the model proposed in this paper is also applicable, and together with the algorithm in Fig. 7,yields optimized results.However,the relationship between the geometric parameters of the planar detector(Fig. 1)must be recalculated.That is,to apply the proposed model to the 3D detector, the relationship between geometric parameters must be solved again. A mathematically feasible approach is to use the symmetry of the 3D detector microstructure to solve by parts. For example, if the 3D microstructure is axisymmetric, then it can be solved by the radius with the center of symmetry being the center of a circle, determining the geometric relationship at a fixed radius, and then solving using the method given in Sect. 2.

4.3 Effects of energy spectrum hardening

For the thermal neutron spectra considered in this study,the cross sections interacting with matter approximately obey the 1/v law. As neutrons penetrate the sample, lowenergy neutrons decay more rapidly than high-energy neutrons, ultimately increasing the proportion of higherenergy neutrons in the neutron energy spectrum, a phenomenon known as energy spectrum hardening.

The current solution to this problem is to define an‘‘effective neutron cross section to correct for the energy spectrum.Considering that the macroscopic cross section is no longer a constant,the neutron transmittance is no longer simply exponential in relation to the thickness of the sample, even in the absence of scattered neutrons. Therefore, the energy response of the detector should also be considered.We can define an effective cross section based on the ratio of the incident neutron intensity to the transmitted neutron intensity as

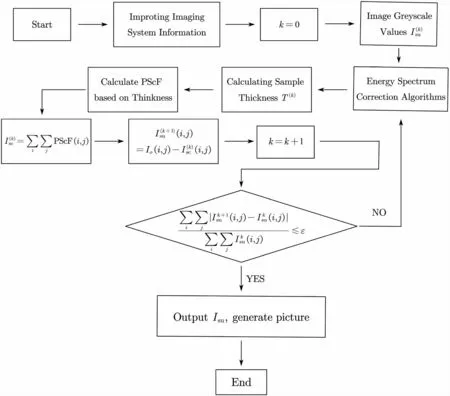
Fig. 7 Neutron radiography quantitative analysis iterative algorithm flow chart

where -Σeff(T )represents the effective cross section for a sample of thickness T.

The intensity of the neutrons detected by a detector is typically expressed by the following equation:

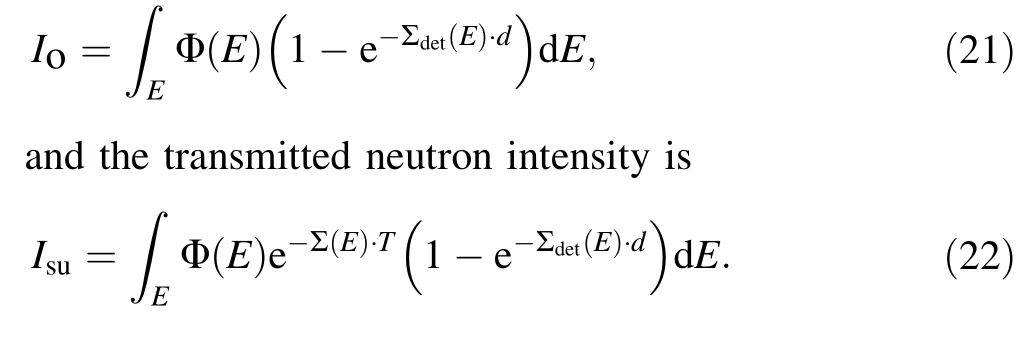
According to the 1/v law, which is approximately satisfied by thermal neutrons,the conventional neutron cross section can be expressed as

where Eth≈0.025eV is the energy of a thermal neutron.Considering the detector energy response as a whole,ε(E )=1-e-Σdet(E)∙d≈Σdet(E )∙d, and combining the above equations yields

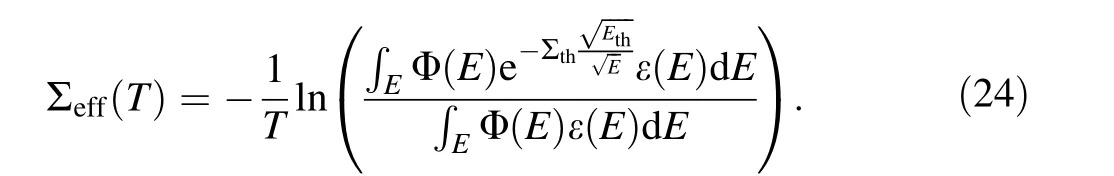
However, owing to the difficulties of performing integration operations and in obtaining relevant data, use of a simplified approximation of the above equation is desirable.The approach taken in[17]is to apply a linear fit,but we believe that the error in doing so would be very large.Instead,we can adopt a numerical integration approach,as described in Sect. 2.2 to approximate the above equation.Again applying the Newton-Cotes method, let

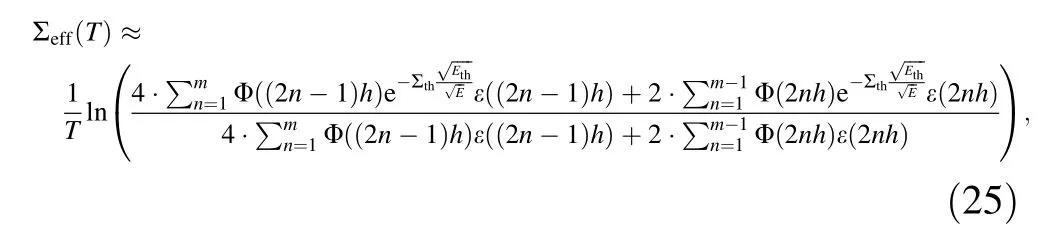
where h is the set step size,and note that φ(E)=0 at both E=0 and E =∞. With the introduction of the effective cross section,the use of an effective cross section to correct the energy spectrum can make the decomposition lines of the spectrum more visible, so that the edges of the sample or large variations in density are more clearly reflected in the image.

However, it would be preferable to make certain modifications to NPScF (r ), i.e., Eq. (15), to achieve an improved energy spectrum correction.

Maxwell’s spectrum can be formally defined as φ E( )=aE exp(-E/b), and the hardening of the energy spectrum is essentially an excess retention of fast neutrons and an excess depletion of slow neutrons, and is therefore reflected in an increase in the parameter b.Considering the specific form of Maxwell’s spectrum, an increase in parameter b is equivalent to an increase in the background temperature. Thus, we can perform the following transformations to account for these factors.

The temperature-corrected energy spectrum is then used in the step calculations. Parameter λ can then be determined by fitting the specific energy spectrum to Eq. (26).

Substituting the corrected energy spectrum into Eq. (13)and replacing the mean scattering cross section with the effective scattering cross section in Eq. (25) yields

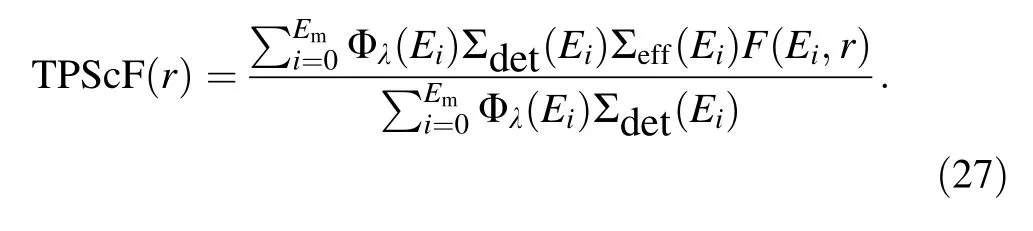
Subsequently, we can correct for the error by applying error analysis, as discussed in Sect. 3.2, by choosing a suitable exponential function based on the symmetry of the spatial distribution.

5 Conclusion

In this study, an approximate point scattered function is investigated for the correction of neutron photographic imaging.The modeling is carried out in Sect. 2.1,whereas Sect. 2.2 explains how the algorithm is used to carry out the calculations.

In the simulation experiment described in Sect. 3, the results shown in Fig. 3 demonstrate the validity of the model. The model was then corrected for the relative error results shown in Fig. 4. This correction is reflected in the addition of an exponential function to adjust for the error(see Eq. 15), and the parameters are determined using the fitting method to finally obtain Eq. (16) to produce satisfactory simulation results. Figure 5 shows the validity of the correction,indicating a mean relative error of 2.5%for the entire neutron converter.

In Sect. 4, we apply the model to the popular quantitative neutron photographic analysis algorithm and find that replacing the conventional point scattered function with the proposed approximate point scattered function results in better neutron imaging, faster convergence of the algorithm, and a significant reduction in the number of iterations. In addition, we investigated the effect of energy spectrum hardening on neutron photographic imaging,concluding that energy spectrum hardening is equivalent to increasing the background temperature in Maxwell’s spectrum, and therefore, a temperature correction parameter can be introduced (Eq. 26). After replacing the mean scattering cross section with the effective scattering cross section and including the temperature correction, a new point scattering function is given by Eq. (27). Finally, the error analysis method applicable to the proposed model is discussed.

Author contributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Lin-Feng Ye,Wei-Jun Jiang and De-Hong Gao. The first draft of the manuscript was written by Jia-Yu Ni and Jun Qin and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.

Author contributionsAll authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Lin-Feng Ye, Wei-Jun Jiang and De-Hong Gao.The first draft of the manuscript was written by Jia-Yu Ni and Jun Qin and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.