基于CS算法的城轨列车自动驾驶控制策略研究

吴秋艳

(南京交通职业技术学院，江苏 南京 210012)

0 引言

城轨列车的运行过程具有非线性、高复杂性等很多不确定性的特点，而传统的控制方法往往需要精确的数学模型，因此传统控制方法对于城轨列车运行过程的研究具有很大的局限性。国内外学者很早就将研究方向转向具有自学习、自适应、自诊断能力的智能控制相关领域上来，利用智能控制方法来处理对象的复杂性和不确定性，解决传统控制方法无法解决的复杂控制问题。目前，对于城轨列车智能控制方法的研究如多目标粒子群算法[1]、预测模糊控制算法[2]、多模态动态规划算法[3]、差分进化模拟退火混合算法[4]和细胞自动机算法[5]等。除此以外，国内对于列车的精度控制和节能控制，也有相关研究[6-21]。例如，通过设计自适应控制器和使用预测模糊PID控制对列车速度进行跟踪控制，从而提高列车的停车精度；通过改变列车的惰行距离来降低列车的运行能耗；通过不同的列车运行控制方式的组合优化，得到最佳控制策略来实现节能目标等。本文所研究的布谷鸟搜索(Cuckoo Search，CS)算法是由剑桥大学Xin-SheYang教授和S.Deb于2009年提出的一种新兴启发算法。该算法模仿了布谷鸟的繁殖策略，遵循Lévy飞行机制，具有包含参数少、易于操作、寻优能力强等优点。国内对于CS算法的应用研究已经在很多行业中开展，但是在城轨列车自动驾驶方面，相关研究很少。本文以CS算法为基础算法，对列车自动驾驶过程进行仿真分析，比较CS算法用于城轨列车自动控制的优缺点。利用 Matlab仿真列车运行模型，对系统进行功能仿真，验证本文所提理论的正确性和控制方法的可行性。

1 布谷鸟搜索算法(CS)

布谷鸟搜索算法是一种具有全局启发式的智能优化算法。该算法主要基于布谷鸟的巢寄生繁殖机理和lévy飞行原理。其优点是参数比较少、随机搜索能力强。

布谷鸟搜索算法的实现主要是基于下面3个理想化的假设：

(1)每只布谷鸟一次只产一枚蛋，然后将其置于随机选中的一个鸟巢中；

(2)随机选择一组鸟巢后，高质量的鸟巢将传给下一代；

(3)可用的宿主巢的数量n是固定的，宿主以概率Pa发现布谷鸟的蛋，此时，宿主选择将布谷鸟的蛋丢掉或者另建新巢，其中，Pa∈[0,1]。

标准布谷鸟搜索算法遵循lévy飞行机制，即其第i个鸟巢的位置变换遵循以下规律：

(1)

Lévy(λ)∽u=t-λ，1<λ<3

(2)

通过上述规则及位置变换的规律，可以将布谷鸟搜索算法的步骤划分为：

步骤1：设定目标函数并进行初始化；

步骤2：随机产生一组个体，计算并保留当前的最优目标函数值及相应个体，其他个体依公式(1)更新位置；

步骤3：以概率Pa进行集体变异，对于第i个个体，若Pa<γ(一个服从均匀分布的随机数)，则随机产生一个新个体xnew，若xnew优于第i个个体，则进行替换，否则不替换；

步骤4：重复上述步骤2和步骤3，直至达到终止条件，退出循环；

步骤5：输出全局最优解。

2 列车运行多目标优化模型

根据牛顿第二定律，列车的质点运动方程[7]为：

(3)

(4)

式中：t，v和s分别为列车运行的时间、速度和距离；ε是加速度系数；c为列车单位合力。列车受力公式为：

ma=f(u,v)-g(v)-w(x,v)

式中：m为列车质量；a为列车运行合力所产生的加速度；f(u,v)为列车的作用力，分为牵引力和制动力，与输入控制序列u和列车的运行速度v有关；g(v)为列车基本阻力，是列车运行速度的函数；w(x,v)为列车的附加阻力，其中x为线路位置，并且该附加阻力与线路坡度、曲线和隧道等线路条件有关[6]。当列车处于牵引状态时，f(u,v)>0；当列车处于惰行状态时，f(u,v)=0；当列车处于制动状态时，f(u,v)<0。

3 仿真实验与分析

3.1 仿真参数设置

本文所设计的线路参数、坡度参数和列车参数的取值分别如表1、表2和表3所示。

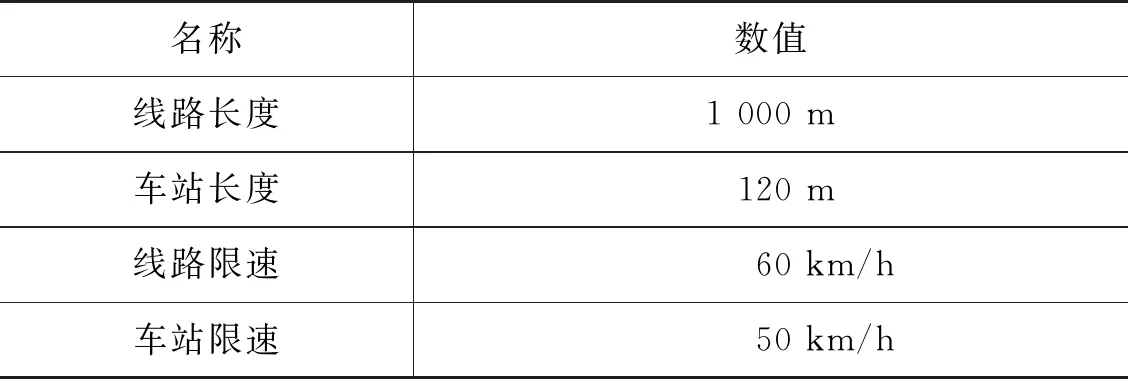
表1 线路参数

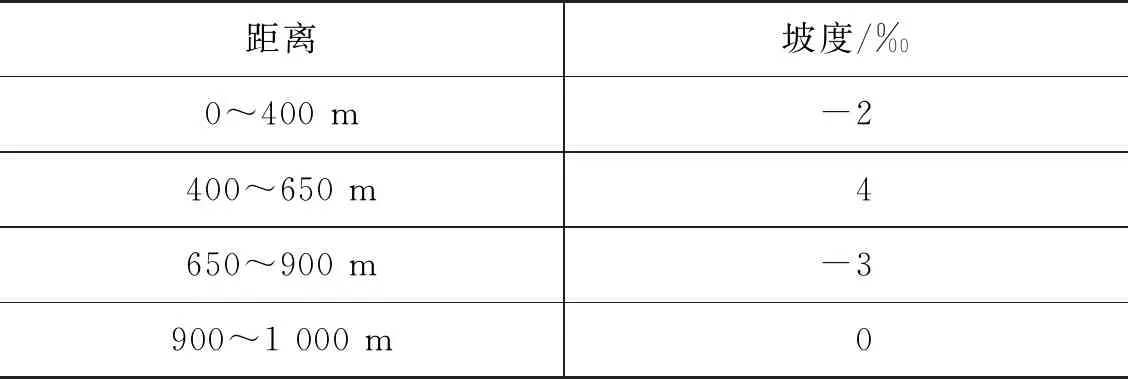
表2 坡度参数

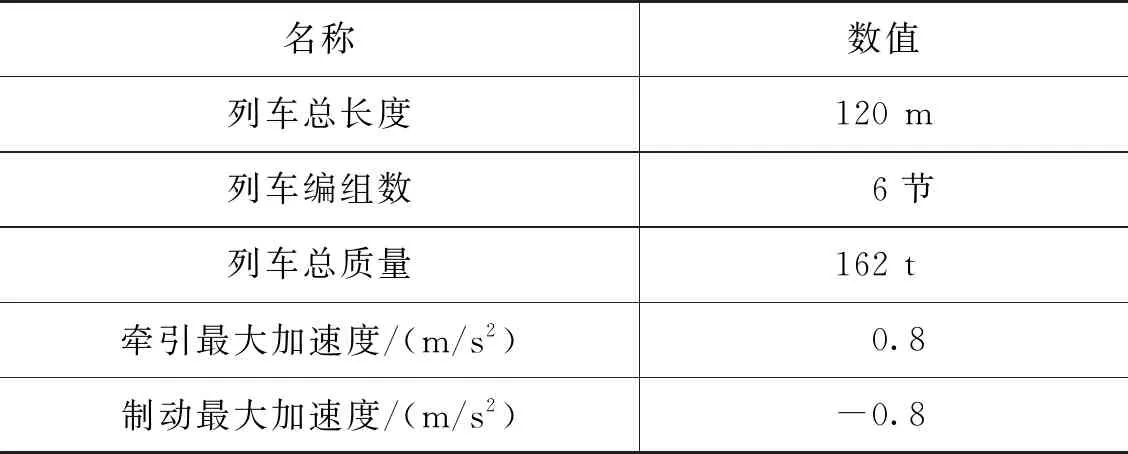
表3 列车参数

3.2 仿真结果及分析

在Matlab环境下对基于CS算法的城轨列车运行过程进行仿真实验，得到速度-距离曲线以及加速度-距离曲线分别如图1和图2所示。

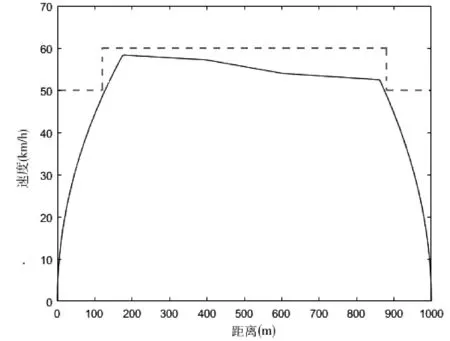
图1 速度-距离曲线

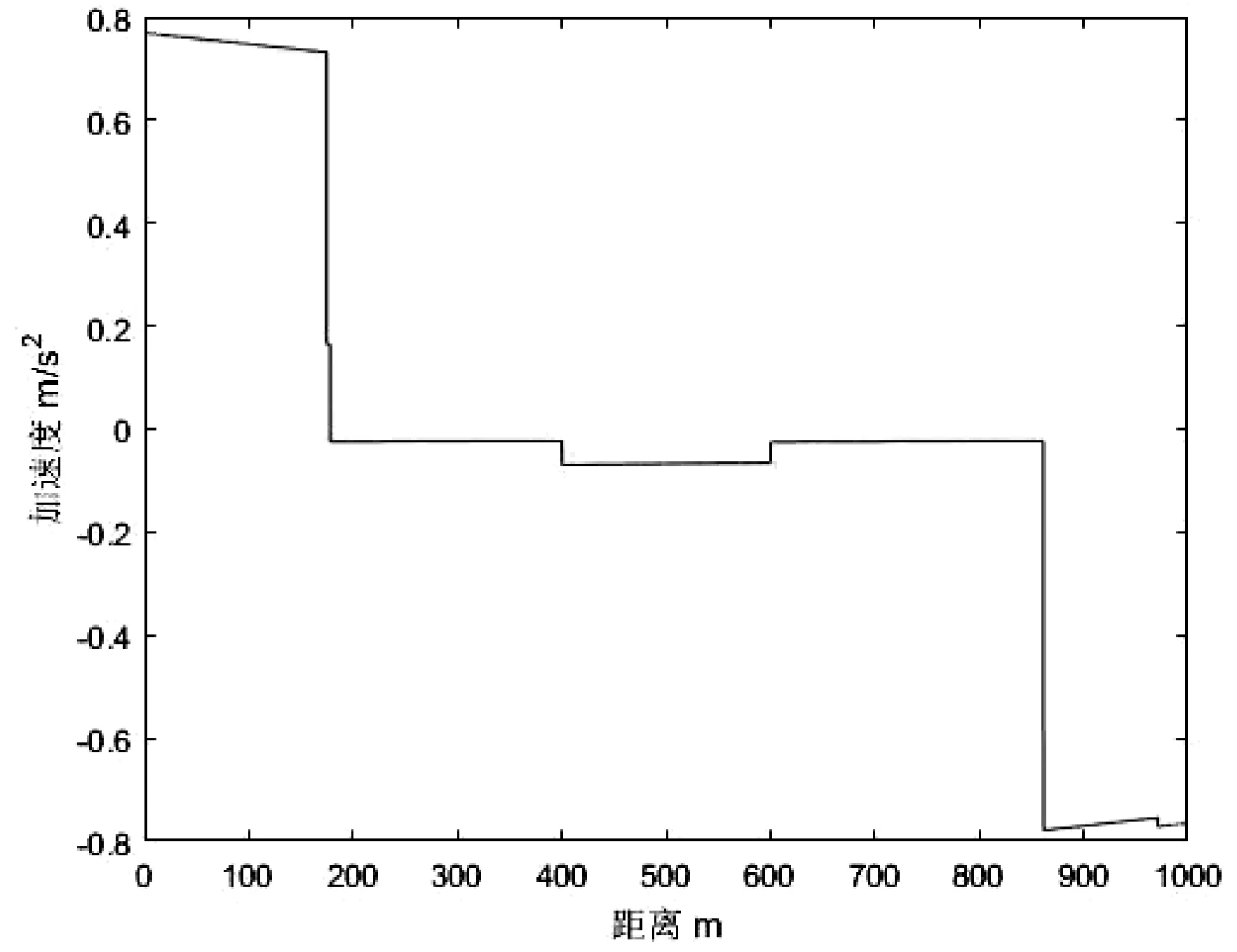
图2 加速度-距离曲线

图1是采用CS算法对列车运行过程优化后得到的速度-距离曲线图。从图1可以看出，运行速度满足表1线路参数表中的线路限速和车站限速的要求，并且在较短距离内实现平稳加速和平稳制动，有效地提高了舒适度。

图2是采用CS算法对列车运行过程优化后得到的加速度-距离曲线图。从图2可以看出，当列车速度接近于限速后，加速度开始下降，并且在列车惰行过程中，列车加速度并没有因为坡度的变化而产生明显变化。对于乘客而言，列车运行中加速度变化率在1 m/s2内都是感觉舒适的，因此可见本算法对于舒适度和能耗的数值优化起到了重要作用。

同时，本文对仿真过程中的停车精度、准点误差、能耗、舒适度也进行了数据记录，结果如表4所示。

表4 CS算法优化结果

为验证本文算法的有效性，对不加算法下的列车运行过程也进行了仿真分析。

如表4所示，在不加以任何算法优化的情况下，列车运行过程中停车误差和准点误差与停车误差小于0.3 m并且准点误差小于4 s的要求相差甚远，因此无法满足运行的基本要求。

当列车运行过程模型采用CS算法优化后，在第400次迭代后，停车误差和准点误差均可以满足上述条件。除了停车误差和准点误差这两个指标外，基于CS算法下的列车运行过程中的舒适度和能耗指标也明显优于不加任何算法的数值。

4 结语

通过仿真和实验，对比不加算法的列车运行过程中的停车误差、准点误差、舒适度以及能耗指标，结合速度-距离曲线图和加速度-距离曲线图，结果表明CS算法对于优化城轨列车运行模型的正确性和可行性，且效果良好。本次的算法模型在收敛速度上仍有欠缺，这一问题可以作为今后CS算法研究的优化方向。