两种卫星天线静态信号质量对比研究

周 鑫

(兰州交通大学，甘肃 兰州 730000)

0 引言

GNSS(Global Navigation Satellite System)是一种可以在地球表面或近地空间的任何地点为使用者提供全天候、全方位的三维位置和速度以及时间信息的导航定位系统[1]。GNSS信号质量的好坏会直接影响到组合导航的定位精度[2]，对于硬件层面而言，采用不同的GNSS卫星信号接收机和天线会在一定程度上影响到接收数据的能力和质量。本文在此基础上，开展对GNSS卫星天线接收信号质量在静态环境下的对比，重点比较卫星颗数、HDOP值以及定位经纬度的方差，分析了不同型号的卫星天线在民用领域应用的前景。

1 GNSS卫星定位基本原理

1.1 伪距

伪距就是由GNSS观测而得到的GNSS观测站与卫星之间的距离。根据卫星信号的发射时间ts与天线收到信号的接收时间tu，可以算出卫星信号传播的时间，再乘以信号的传播速度c就可以得到天线与卫星之间的距离。但是由于卫星时钟和接收机钟之间存在着钟差，同时信号传播的过程中也会受到大气层等其他因素的影响，所以这样直接测得的距离并不等于与卫星之间的真实距离，只能称之为伪距ρ，伪距的表达式如公式1所示。

ρ=c(ts-tu)

(1)

假设卫星天线与卫星之间的真实距离为r，接收机与GNSS时间的钟差为δt，卫星与GNSS时间的钟差为δt,s。考虑到卫星信号在传播过程中会受到大气层的延时，这里以I作为因大气电离层导致的延时，以T代表大气对流层导致的延时，以ε代表其他各种未考虑到的因素及噪声的导致的延时，则r可表示为：

r=c[(tu-δt)-(ts-δt,s)-I-T-ε]

(2)

将公式2展开，可得公式3。

r+c·δt=ρ+c·δt,s-cI-cT-cε

(3)

上式中，等号右边均可认为是已知量，其中I和T都有对应的模型，δt,s的模型也会在也在导航电文中给出，而根据欧拉法则：

(4)

其中(x,y,z)为卫星接收机的位置坐标，(xs，ys,zs)为卫星的位置坐标，将公式4代入公式3中，可得：

ρ+c·δt,s-cI-cT-cε

(5)

该方程式为严格准确的GNSS基定位方程，包含(x,y,z,δt)4个未知数，因此，在不考虑其他误差的情况下，想要获取卫星天线的位置，至少需要4颗卫星。

1.2 载波相位

除了通过伪距来测距之外，载波相位也可以用来测距。GNSS中，L1载波的频率为1 575.42 MHz，波长约为19 cm。在这些已知基础上，测量出传播路径上两点之间的相位差，就可计算出两点之间的距离。

这里假设φu为接收机复制的卫星载波信号的相位，φs为接收机接收到的卫星载波信号的相位，则载波相位测量值可表示为：

φ=φu-φs

(6)

因为载波的波长很短，远小于接收机到卫星的距离，信号传送到地球的过程中，会产生N个周期的差别，这里N称为周整模糊度。进一步设波长为，接收机与卫星之间的距离为γ，则有：

φ=λ-1γ+N

(7)

进一步考虑大气电离层导致的延时I、大气对流层导致的延时T、接收机的钟差δtu以及其他各种未考虑到的因素及噪声导致的相位差φ，则有：

φ=λ-1[γ+c(δtu-δts-I+T)]+N+φ

(8)

根据1.1所得伪距ρ，可以进一步粗略估算周整模糊度N,表示为：

(9)

这里表示取整运算。

1.3 伪距和载波相结合

根据上文可以看出，伪距精度不如载波相位高，但是伪距可以实现绝对定位，而载波相位有一个未知的周整模糊度，无法实现绝对定位，将伪距和载波相位结合必然可以达到更好的定位效果。

这里设ρk为k时刻的伪距测量值，φk为k时刻的载波相位测量值，ρs,k为k时刻的平滑伪距，则有：

(10)

其中，M为平滑时间常数，M值越大，平滑伪距结果就越依赖于载波相位的变化量，结果也就越平滑，这种方法称为利用载波相位平滑伪距法。

根据上文可以看出，伪距精度不如载波相位高，但是伪距可以实现绝对定位，而载波相位有一个未知的周整模糊度，无法实现绝对定位，将伪距和载波相位结合必然可以达到更好的定位效果。

2 卫星信号质量判断因子DOP

精度因子DOP(Dilution of precision)是判断卫星信号质量的重要指标，用于表示各个方向和时钟的误差放大倍数[3]。它是考虑每颗卫星相对于星座中其他卫星的位置来预计用该星座能得到的位置精度的计算结果。小的DOP值表示强的卫星几何位置和精度的较高概率。高的DOP值表示弱的卫星几何位置和精度的较低概率。一个GPS接收器可以在同一时间得到许多颗卫星定位信息，但在精密定位上，只要4颗卫星讯号即已足够了，一个良好的接收器便可判断如何在这些卫星讯号中去撷取较可靠的讯号来计算，如果接收器所选取的讯号中有两颗卫星距离甚近，两颗卫星讯号在角度较小的地方会产生一个重叠的区域，距离越近，此区域越大，影响精度的误差也越大。如果选取的卫星之间有一段距离，则讯号相交之处较为明确，误差当然就缩减了不少。

DOP可根据应用场景不同分为水平精度因子HDOP、高程精度因子VDOP、位置精度因子PDOP、钟差精度因子TDOP、几何精度因子GDOP。PDOP为纬度、经度和高程等误差平方和的开根号值，直接反映GPS卫星的分布情况，当PDOP较大时，表明空中的4颗GNSS卫星几何分布不是太理想，他们构成的图形周长太短，定位精度就低，反之亦然。GDOP是衡量定位精度的很重要的一个系数，它代表GNSS测距误差造成的接收机与空间卫星间的距离矢量放大因子。实际表征参与定位解的从接收机至空间卫星的单位矢量所勾勒的形体体积与GDOP成反比。GDOP的数值越大，所代表的单位矢量形体体积越小，即接收机至空间卫星的角度十分相似导致的结果，此时的GDOP会导致定位精度变差。GDOP数值越小，代表大的单位矢量形体体积，导致高的定位精度。TDOP是指为接收仪内时表偏移误差值，VDOP则是指垂直分量精度因子。但对于地面物体的精度标准而言，HDOP是最重要的指标，HDOP值的大小与GNSS的定位的误差成正比，HDOP值越大，定位误差也就越大，定位的精度也就越低。反之，HDOP值越小，定位误差也就越小，定位的精度也就越高。

3 实验对比

在上述理论分析的基础上，对实验室现有的两个GNSS卫星线进行了接收卫星信号质量的实验。天线一为司南导航公式生产的AT330系列GNSS天线，该天线可接收BDS BD1/BD2，GPS L1/L2，GLONASS L1/L2频段的卫星信号；天线二为东盛通讯器材有限公司生产的900/2700-SGBNN-II型机车专用天线，可接收BD2、GPS L1/L2频段的卫星信号，两种天线的实物图如图1～2所示。

图1 AT330 GNSS天线

图2 900/2700-SGBNN-II GNSS天线

实验环境为一空旷楼顶，无建筑物、树木遮挡，通过采用同一卫星接收机板卡，利用两种不同的卫星天线各采集1 740 s的实时数据，对两种天线的卫星信号质量进行比较。本文主要比较对象为采集数据中的卫星颗数、HDOP值以及经纬度坐标信息。如图3～5所示，分别为两种卫星天线的卫星颗数对比图、HDOP值对比图以及定位经纬度坐标对比图，表1则显示了两种天线的卫星颗数的平均值、HDOP的平均值和方差、定位经纬度数据的方差。

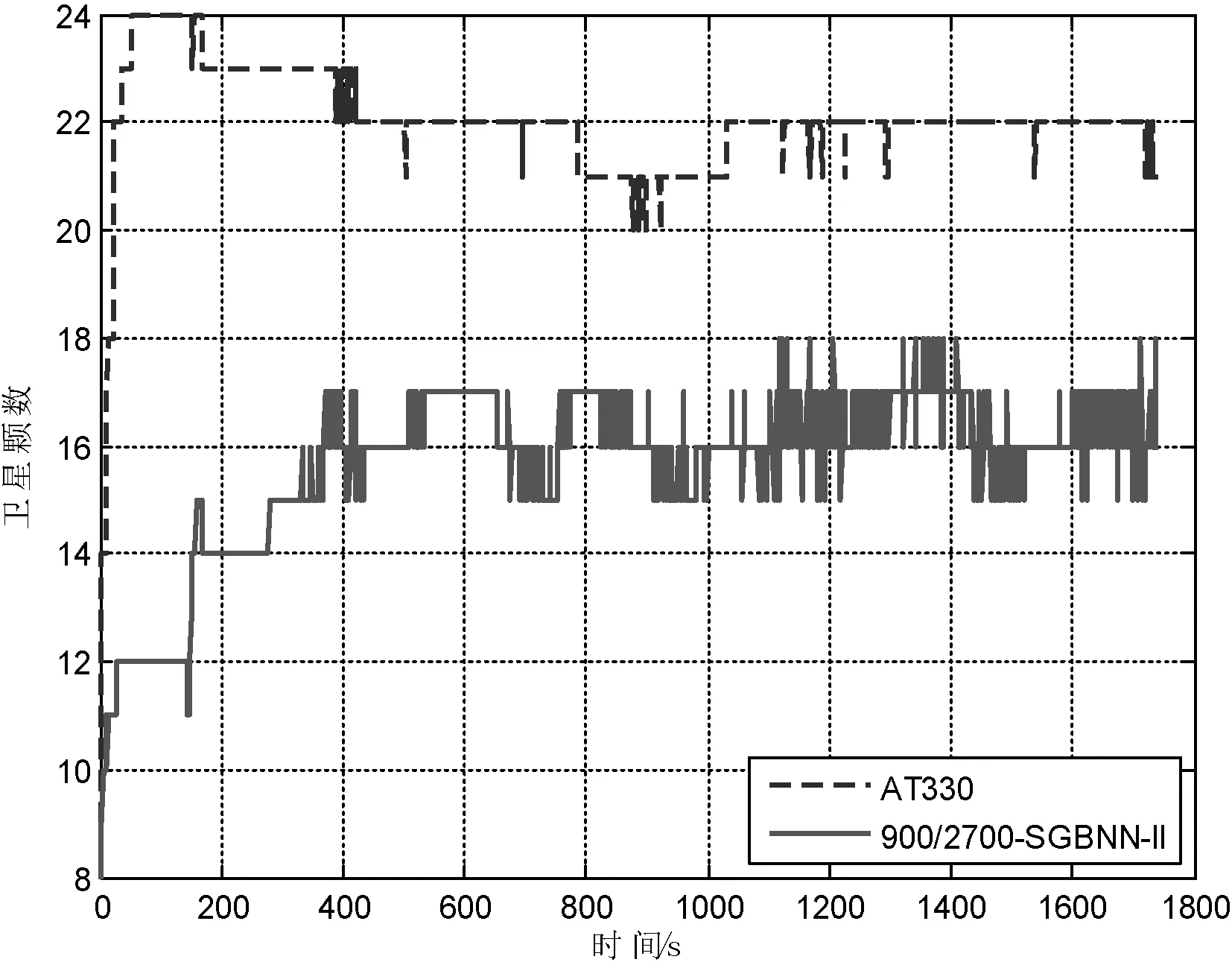
图3 两种卫星天线的卫星颗数对比

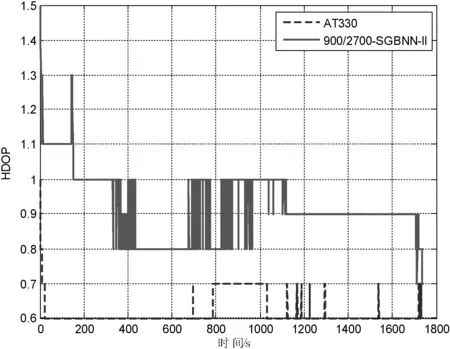
图4 两种卫星天线的HDOP值对比

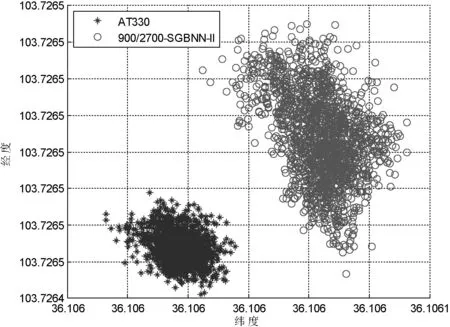
图5 AT330天线采集数据定位

表1 两种天线方差对比

AT330平均搜星颗数为22，最多可达24颗；而900/2700-SGBNN-II平均搜星颗数为15.67，最多可达18。从HDOP值来看，AT330平均HDOP为0.63，最高为1，最低为0.6，方差为1.095 4；900/2700-SGBNN-II平均为0.93，最高为1.5，最低为0.7，方差为1.520 5。从定位稳定性上来看，AT330的纬度方差为2.89E-06，经度方差为2.04E-06；900/2700-SGBNN-II纬度方差为4.94E-06，经度方差为5.94E-06。经过对比可以看出，无论是从搜星颗数还是HDOP值的大小以及定位的方差，AT330均优于900/2700-SGBNN-II。

4 结语

本文通过静态定点实验完成了对AT330型号卫星天线和900/2700-SGBNN-II型号卫星天线的对比分析，通过比较两种天线的卫星信号质量，可发现，相较于900/2700-SGBNN-II，AT330卫星天线的卫星信号质量更好，定位效果更加稳定。