基于改进的卡尔曼滤波无人机抗欺骗BDS导航方法
王秀境,肖建华,刘岑俐,陈肖,杨诚
(贵州电网有限责任公司凯里供电局,贵州 凯里 556000)
伴随着无人机产业化的发展和普及,无人机也广泛应用在各个行业。特别在电力巡检等传统上需要借助人工检查的工作,通过无人机自主巡检,可以降低人工巡检成本,同时可以对巡检物进行全方位的检查,从整体提高了电力巡检的效率。然而,由于卫星导航信号的脆弱性,基于卫星导航技术的无人机作业容易受到干扰和欺骗,从而使得其航向偏离,严重时无人机会被欺骗信号引导,造成经济损失。近年来,干扰欺骗逐渐成为阻碍无人机工作效率的严重问题之一。因此,研究无人机抗干扰欺骗技术,对保障无人机的安全,提高巡检的工作效率具有重要的意义。
目前基于GPS系统的静态场景的抗欺骗研究较多,主要分为3类:(1)天线改进技术,主要有双天线 抗欺骗技术[1-2]、多天线抗欺骗技术[3-5]以及移动单天线抗欺骗技术[6];(2)测量一致性方法,主要有接收机自主完好性监测技术[7-8]、相关峰畸变监测技术[9-10]、伪距变化率和多普勒频率一致性检测[11]、组合导航信息一致性抗欺骗技术[12-13];(3)锁相环改进方案,主要有多径估计延迟锁相环[14-15]、耦合调幅延迟锁相环[16-17]、序贯最大似然估计[18-19]。这些抗欺骗的技术针对大部分静态终端欺骗场景均可显示出抗欺骗的性能。然而考虑到成本和用户特性等因素,这些技术无法推广应用。
作为卫星接收端,无人机的状态特征是具有动态性。传统用于静态抗欺骗定位算法不适用于无人机的抗欺骗导航,这是因为滤波过程中的观测值出现跳变,滤波器并不能自适应观测值变化所产生的影响,破坏整个滤波过程,模型无法获得最优状态估计,从而导致定位结果的发散。对于动态终端抗欺骗的研究,文献[20-21]在GPS动态定位情况下将自适应卡尔曼滤波模型和自适应算法相结合,改进了GPS定位卡尔曼滤波器的跟踪性能。文献[22]针对GPS高动态终端的运动特点,将 UD 分解滤波算法与卡尔曼滤波模型相结合,使得算法具有稳定性和快速收敛的特点。 文献[23]利用扩展卡尔曼滤波器实现高动态物体的高精度GPS定位。文献[24-25]提出差分数据处理与卡尔曼滤波模型相结合,在牺牲一定精度的情况下,实现抗欺骗设备低成本化。以上的文献中提到的针对 GPS接收端的高动态定位,主要是基于卡尔曼滤波算法,有的只考虑定位精度,有的只考虑解算稳定性。然而,目前没有一个算法在既保证定位精度的同时,兼顾解算稳定性。
本研究通过引入两种方法,在欺骗环境下,兼顾无人机的BDS的定位精度和稳定性。一方面,引入消减因子,对当前测量信息赋予较高权值,降低历史状态信息的比重,进而保障了滤波解算的稳定性。另一方面,用统计学中的M-估计理论,修正增益系数,以确保定位估计值尽可能接近无人机真实位置。
1 北斗卡尔曼滤波定位测速原理
1.1 北斗接收机定位
传统的N维离散系统的卡尔曼滤波器的定位和测速状态方程和观测方程为:
Xk=Φk,k-1Xk-1+Γk,k-1Wk-1
(1)
Zk=h[Xk,h]+Vk
(2)
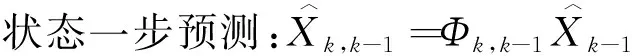
(3)
状态估计:
(4)
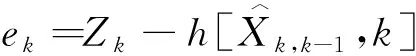
(5)
滤波增益:
(6)
一步预测均方误差:
(7)
均方误差估计:Pk=[I-KkHk]Pk,k-1
(8)
式中:Xk为系统的n维状态向量;
Zk=(ρ1,k,ρ2,k, …,ρN,k)为系统的m维观测向量;Wk为p维系统过程噪声向量;Vk为m为观测噪声序列;Φk,k-1为系统n×n维状态转移矩阵;Γk,k-1为n×p维噪声输入矩阵;h[Xk,h]为m维向量函数;Hk为m×4维的转移矩阵。Rk是观测噪声方差;Qk表示系统噪声方差。
1.2 北斗接收机测速
无人机在作业飞行状态时,BDS定位测速可以采用伪距变化率。通过伪距差分等方式获得伪距的变化率等信息,BDS接收机估计位置和速度。伪距变化率表示为:
(9)
2 无人机北斗抗欺骗定位
在欺骗信号环境下,动态的无人机需要兼顾欺骗信号识别和定位结果稳定两方面问题,本文引入消减因子保证卡尔曼滤波器稳定性,引入 M -估计理论以保持定位估计的精度,算法总体流程如图1所示。在无人机接收端,获得伪距测量值和卫星广播星历。基于接收端的信息,改进卡尔曼滤波模型进行无人机定位,同时,通过伪距测量的估计值和实际值,估计无人机的速度。当系统没有受到干扰欺骗时,无人机进行正常飞行作业,记录定位结果。当无人机受到干扰欺骗时,基于改进的卡尔曼滤波模型通过其抗欺骗能力,输出抗欺骗的定位结果,同时,系统进行状态告警。
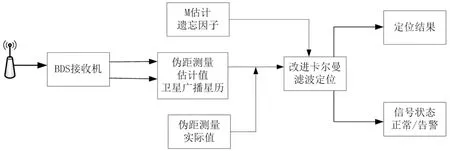
图1 无人机BDS抗欺骗改进卡尔曼滤波算法流程Fig.1 UAV anti-spoofing adaptive Kalman filter algorithm flow
2.1 模型稳定性增强——消减因子
采用消减因子限制卡尔曼滤波器中历史信息对当前状态的影响,进而充分利用当前的观测数据。消减因子主要是在状态估计误差(公式(7))前的协方差阵乘一个加权系数,即:
(10)
λk=max{1trace(Nk)/trace(Mk)}
(11)
(12)
(13)
(14)
式中:λk为消减因子,λk≥1,trace(·)是矩阵求迹符号。
由此可见,在欺骗环境下,卡尔曼滤波的估计误差将增加,从而使得误差方差阵增大,同时消减因子随之增大。这样,使得滤波器的跟踪能力增强,模型的稳定性也随之增强。
2.2 模型精度改进——M-估计
由BDS定位原理可知,欺骗干扰信号对无人机定位的影响主要产生在新息估计处。因此,在欺骗干扰出现时,即刻通过算法修正增益系数,进而消除其对估值精度的影响。
对于观测方程(2),残差的函数定义为:
(15)
式中:f(·)是标量函数,n是观测向量维数,Zki是在k时刻观测向量中第i个元素,hi是观测矩阵H的第i行。残差最小化可以通过对残差求导,并使之等于0而获得。
取M估计:
(16)
(17)
式中,Ψ(·)是f(·)对于位置矢量的导函数
写成矩阵的形式为:
HTD(e)e=0
(18)
式中:D(e)=diag(D(e1)D(e2)…D(en))
在欺骗干扰环境下,北斗接收机能够继续提供准确的导航信息,需要达到的目的是:测量误差增大,不影响对状态结果的估计。因此,M-估计的加权矩阵定义如下:
(19)
本文引入统计学中的M -估计,通过状态估计(公式(4))中加入M估计量,改进新息的加权矩阵,减少欺骗干扰信号对无人机飞行定位造成的影响,如公式(20)所示:
(20)
3 仿真与分析
3.1 仿真描述
为了验证本文提出的高动态定位下基于自适应卡尔曼滤波的抗欺骗干扰方法。接收机加速度和加加速度按照下图2和图3所示设置。为了保证仿真的可用性,分别设置了两个周期。
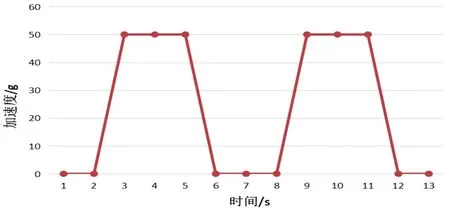
图2 BDS无人机加速度设置Fig.2 UAV BDS receiver acceleration setting

图3 BDS无人机加加速度设置Fig.3 UAV BDS receiver jerk setting
仿真采样625个点。设置欺骗式干扰分别出现在100 -300,400-600的采样区间上。欺骗干扰产生的附加伪距设置为500m。其中观测噪声方差阵R0和系统噪声方差阵Q0分别设置为:
(21)
(22)
3.2 实验分析
为了验证本文提出的改进卡尔曼滤波算法的性能,引入经典卡尔曼滤波的定位算法结果作为参考。对于动态无人机,设置其以匀速15m/s运行,当引入欺骗干扰后,无人机的定位结果与预设的无人机运行轨迹比较,其解算的速度结果与预设的速度比较,分别获得定位和测速误差。
(1)经典定位算法
在欺骗干扰存在的情况下,无人机飞行中的定位残差和速度残差如图4和图5所示。

(a) X轴定位残差(a)Position residuals of X axis
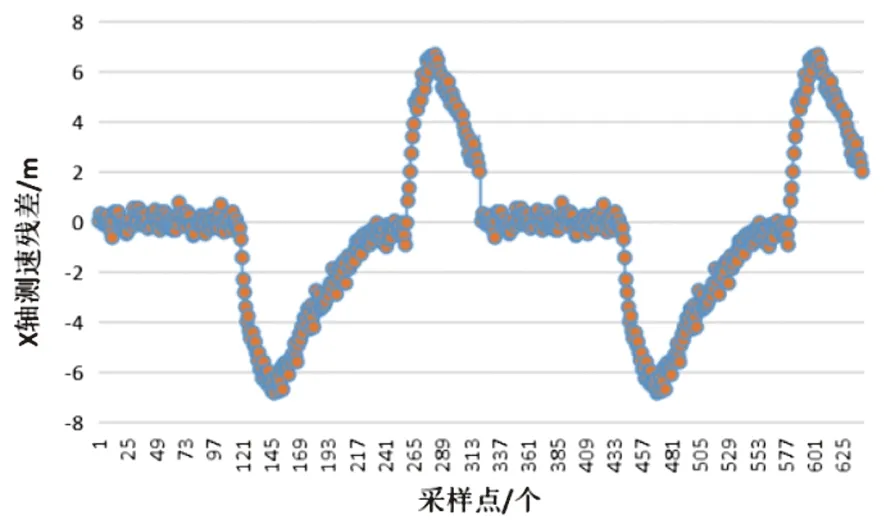
(a)X轴测速残差(a)Speed mesurement residuals of X axis
以上图可知,在无人机飞行情况下,加入欺骗干扰后,基于经典的卡尔曼滤波的定位和测速结果受到较大影响。定位的三维方向分别偏离了约500m,这与附加的伪距偏差相对应,也说明接收机受欺骗信号的干扰使得航道产生了偏移。速度解算中也出现了速度偏移的现象。由此可见,引入欺骗信号的情况下,经典卡尔曼滤波器模型的稳定性被破坏、其抗欺骗干扰的能力较差。因此,经典卡尔曼滤波无法满足高动态下的无人机北斗抗欺骗干扰的需求。
(2)改进卡尔曼滤波算法
采用本文提出的改进卡尔曼滤波模型,在欺骗干扰情况下,无人机定位残差和测速残差如图6和图7所示。

(a)X轴定位残差(a)Position residuals of X axis
从图6和图7可以看出,当引入欺骗干扰信号时,在无人机飞行情况下,采用本文改进的卡尔曼滤波模型,其定位残差约为 5.95m,而测速残差约为0.41m/s 。可以看出,在引入欺骗信号的情况下,无人机飞行受到欺骗信号的影响很小,改进的卡尔曼滤波模型的定位稳定性比较经典的卡尔曼滤波器的性能有较大的提升。
(3)定位性能比较
图8绘制出引入欺骗干扰情况下,无人机仿真飞行的轨迹。图中红线表示无人机飞行的仿真运动轨迹,蓝线表示基于经典卡尔曼滤波模型计算出的无人机运动轨迹,绿线表示基于本文的改进卡尔曼滤波模型获得的无人机运行轨迹。可以看出,加入欺骗信号后,基于经典卡尔曼滤波模型的轨迹出现了明显的偏移,而基于改进的卡尔曼滤波模型的轨迹基本接近预设的仿真轨迹。这进一步证明了本文提出算法在无人机飞行情况下,具有良好的抗欺骗干扰性能。
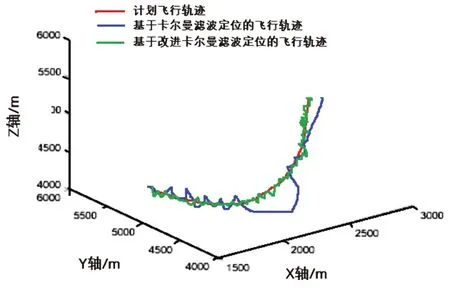
图8 引入欺骗干扰信号的情况下,无人机飞行定位轨迹Fig.8 Under spoofing, UAV BDS positioning trajectory
4 总结
无人机具备BDS抗欺骗技术,对其保证作业效率和作业安全具有非常重要的作用。然而,对于作业中的高动态无人机,其接收端的测量值快速变化,会使其定位解算发散。同时,传统的卡尔曼定位算法无法抵抗欺骗信号的干扰,会使得无人机偏离航道,影响作业安全同时造成经济损失。
针对欺骗信号环境下,无人机作业的定位发散和欺骗信号识别困难的问题,本文基于传统的卡尔曼滤波定位模型进行了改进,通过引入统计学中的M-估计来保持定位精度,引入消减因子来保证定位结果的稳定性,从而建立了一种针对高动态无人机的改进的卡尔曼滤波定位模型。仿真实验表明,在引入欺骗信号的情况下,基于改进的卡尔曼滤波模型性能稳定,可以有效地保证无人机飞行定位的准确性和稳定性,具备抗欺骗的能力。
本研究主要基于仿真分析,对本文提出的算法进行对比验证。下一步工作将建立抗干扰欺骗检测平台,实时监测和显示无人机作业的状态信息,对于干扰欺骗情况下提出告警。同时,研究以卫星授时为主的电网的时间频率网络系统[26-29]的抗欺骗性能,进一步验证和改进算法。

