基于网络特征的分层剪枝方法

洪 亮, 高 尚, 李 翔

(吉林大学 计算机科学与技术学院, 长春 130012)

深度神经网络[1-2]目前已广泛应用于图像分类、 物体检测、 生物学研究、 语音合成和语义分割等领域[3-4]. 复杂网络体系常具有一个体积巨大的模型, 消耗了大量的计算资源和能源. 当在资源受限的设备上部署使用深度神经网络时, 模型过大导致的问题尤为突出[5].

模型压缩可通过裁剪掉一部分参数、 改变数据的存储方式或设计网络结构减少模型的体积. 作为模型压缩的方法之一, 模型剪枝技术[6]已被证明是一种有效的方法[7-11], 可在尽量不损失精度(甚至更好)的情况下减小模型体积. 在剪枝技术中, 基于权重的剪枝是一种常用方法. 在范围上, 剪枝技术可分为全局剪枝和分层剪枝. 分层剪枝方法对每层的参数单独进行处理, 如果某个参数低于该层的重要性最低阈值, 则将其裁剪掉. 例如： 使用权重的绝对值衡量重要性, 先移除权重值低于阈值的所有参数, 然后重新训练剩余的稀疏网络[8]或将剩余权重恢复到初始状态再进行训练[12]； 基于进化算法评估各层对权重剪枝的敏感度, 进而决定每层的剪枝率[13]； 使初始剪枝率渐变到目标剪枝率, 使之适应训练过程[14]； 基于相互信息自顶向下地进行剪枝, 对于神经网络的每层, 相互关系值高于上一层保留神经元的, 可以继续保留[15]； 通过评估各层对特征表示的贡献判断各层重要性[16]等. 此外， 常见的还有优化激活函数[17]、 进行通道剪枝、 知识蒸馏[18]等. 但很多当前的分层剪枝方法所提出的重要性衡量标准都是针对单独某层的特点, 或者仅考虑了相邻层的关系, 进而决定每层的剪枝率. Frankle等[12]的彩票假说实验结果表明, 采用单剪枝率的分层剪枝方法在效果上并不如全局剪枝. 这是因为网络的层与层之间的信息传递是不同层次的[19], 每层对于剪枝的敏感度也不相同[8-10]. 而当前很多分层剪枝方法对网络层与层之间关系的利用并不充分.

针对上述问题, 本文提出一种基于网络特征的分层剪枝方法NS-LPM(network-structure based layer-wised pruning method), 综合考虑网络结构的信息及网络各层次间的关系, 以解决分层剪枝方法的适用性问题. 网络特征包括3个维度: 网络的深度、 每层的宽度以及层间参数的重要性. 本文实验分别从这三方面讨论它们对剪枝方法的影响和有效性. 为更准确地去探讨这3个维度的影响, NS-LPM实验基于彩票假说实验[12]进行. 每次剪枝后, 将每层保留的权重回溯到初始网络值, 以尽量减少除网络结构特征外的影响.

本文针对不同的网络特征在数据集CIFAR-10上分别采用VGG-16和Resnet-20网络架构进行对比实验, 以探讨不同的剪枝率变化方法对该指标的影响. 实验结果表明, NS-LPM方法在VGG-16模型上表现良好, 优于全局剪枝方法和传统单剪枝率的分层剪枝方法； NS-LPM方法在Resnet-20模型上的表现优于传统单剪枝率的分层方法, 接近全局剪枝方法. 其在相同压缩率下的准确率更高, 且在训练初期收敛更快； 在训练后期可以自适应地降低剪枝率, 尽量避免网络性能突然下降. 为传统分层剪枝方法的应用受限情况提供了一种新的解决方案.

1 预备知识

过度参数化是深度神经网络被广泛认可的特性[20], 但会导致推理的高计算成本和高内存占用. 相关研究表明, 对一个过度参数化的、 足够大的网络进行训练非常重要[21], 因为其可提供更强的表达能力, 压缩大网络可得到比直接训练一个小网络更好的结果. 模型剪枝作为模型压缩的一种方法被广泛关注主要有两方面原因: 第一, 训练一个大的、 过度参数化的网络很重要[22], 因为其提供了一个高性能的模型, 给予模型更强的表示能力和优化能力, 且在模型中裁剪掉一部分不重要的参数, 不会明显影响精度； 第二, 修剪后的架构及其相关权重是获得最终有效模型的关键, 剪枝后剩下的权重常具有深远的影响.

本文提出一种基于网络特征的分层剪枝方法NS-LPM, 对网络结构如何影响剪枝过程进行研究. NS-LPM方法采用迭代剪枝流程并进行了改进. 同时, 为尽量减少其他因素对实验的影响, 实验基于彩票假说, 每轮剪枝后都将网络参数恢复到剪枝前的初始状态.

1.1 迭代剪枝流程

剪枝流程主要分为一次性剪枝和迭代剪枝两类. 典型的迭代剪枝过程包括3个阶段： 预训练、 剪枝和微调. 在迭代剪枝流程中, 如何确定重要性并通过重要性评价标准对网络进行裁剪是一个研究热点[9-10,23]. NS-LPM方法采用迭代剪枝流程给出了如何根据网络结构特征确定重要性以及它们作为评价标准的实验效果.

1.2 彩票假说实验

当前的深度神经网络具有过度参数化的特性. 实验和相关研究结果表明, 在满足过度参数化的条件下, 彩票假说值得信赖[24]. 彩票假说的主要内容是： 在一个足够大的网络模型中, 存在一个稀疏子网络(即彩票)可在不高于完整网络的训练次数内, 达到初始网络的相似性能. 而寻找这个稀疏子网络的过程主要应用迭代剪枝和全局剪枝. 特别地, 剪枝后保留的参数并未使用训练后的值, 而是恢复到初始网络值. 实验结果表明, 在使用小型数据集的情况下(如MNIST,CIFAR-10), 实验中的网络剪枝率在50%～90%时通常有更好的性能, 有些网络在剪枝率达到95%以上时仍能得到相同的性能. 如果使用大型数据集, 可在此基础上使用延迟回溯的方法[25].

目前, 对彩票假说的研究已有许多结果, 例如： 分析剪枝过程中的掩码是如何影响训练过程的[26]； 证明彩票假说有效性, 并给出更普适的应用条件[24]； 将彩票假说实验的方法应用于其他网络模型[27]； 研究基于彩票假说的剪枝方法[28]等. NS-LPM实验主要基于彩票假说, 并提出一种基于网络特征的分层剪枝方法. 这主要是因为： 1) 实验中使用标准的迭代剪枝流程和全局剪枝, 是剪枝领域广泛使用的训练基准； 2) 将剪枝后的参数回退到初始状态, 可尽量减少网络中其他因素的干扰, 更好地体现网络结构对剪枝过程的影响； 3) 彩票假说实验已经被大量研究和实验证明是高效准确的.

2 算法设计

基于网络特征的分层剪枝方法NS-LPM采用迭代剪枝流程. 为充分利用已训练网络的结构特征信息, 研究网络特征对剪枝过程的影响, 本文算法分别从三方面进行实验与研究： 网络的深度、 每层的宽度和层间重要性评估. 算法流程如图1所示.

图1 基于网络结构分层剪枝方法的算法流程

基于网络特征分层剪枝方法的第k层剪枝率定义为

(1)

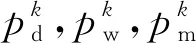
1) 训练好一个大的网络模型；

2) 遍历网络的每层, 对于网络中的第k层参数：

④ 通过剪枝系数计算得到每层的动态剪枝率pk；

3) 对剪枝网络进行微调再训练, 以恢复由于参数裁剪带来的准确度损失；

4) 当网络剪枝周期到达上限或压缩率达标时则结束, 否则转步骤2).

一轮的剪枝流程如图2所示.

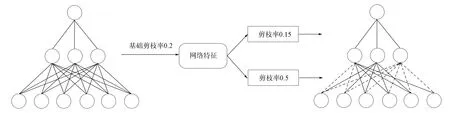
图2 基于网络特征的分层剪枝方法

2.1 网络深度

Ro等[19]研究表明, 网络每层参数对于特征的提取均具有不同的特点[29], 即低层(靠近输入端)会提取相对通用的特征, 而高层(靠近输出端)会提取针对任务的特征. 文献[19]进行了一组对比实验, 实验采用训练好的Resnet网络, 分别将完整网络和移除最高两层的网络直接迁移到其他类似的数据集中测试, 发现移除最高两层的网络明显优于未移除前的完整网络. 表明高层提取的特征对之前的特定任务很重要. 文献[19]的研究还表明, 网络低层的权重变化水平明显大于高层, 并且随着训练每层的变化率逐渐减小. 实验采用Resnet-50网络, 第一层的权重变化率可达到最后一层的十几倍. 即在低层的权重更容易实现从小变大, 权重在某时刻的重要性更有可能在下一时刻突然翻转.

在一个训练好的网络中, 高层提取的特征针对特定任务尤其重要, 如果高层的剪枝率较大, 则显然会更多地影响模型的性能, 使低层的权重变化率较大. 因此为得到更稳定的模型, 降低了低层和高层的剪枝率. 算法期望网络模型的变化趋势如图3所示.

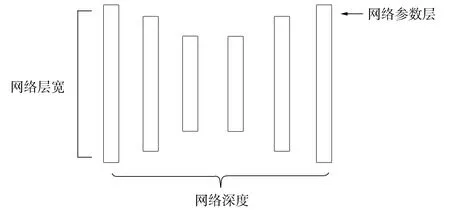
图3 网络层宽随网络深度的变化期望

基于上述分析, 将基于网络深度评价标准的第k层剪枝系数定义为

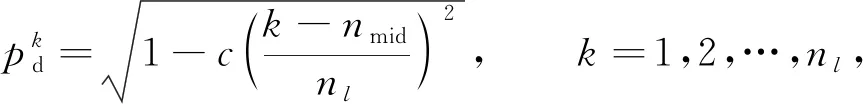
(2)

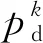
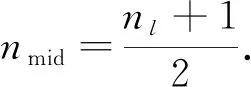
(3)

简单地说, 就是调低高层和低层的剪枝率, 向中间层渐近式地提高到目标剪枝率.高层和低层的变化空间通过降低高层和低层的剪枝率控制.剪枝率将在中间层变缓并保持稳定, 进而快速压缩中间层网络的权重, 加快模型的收敛, 增强模型的稳定性.

2.2 网络层宽

低秩分解是模型压缩的一种常用方法.矩阵的低秩稀疏分解是经典机器学习方法, 假设一个大规模矩阵可分解为两个或多个低维度矩阵的乘积与一个稀疏矩阵的和, 则可极大降低原矩阵表示的元素个数[30].如果网络在深度上是充分冗余的, 则可尝试进行大量剪枝, 裁剪为多个低维度矩阵, 通过训练使其逼近一个高维度矩阵, 并达到几乎相同的性能和效果.在高维度矩阵大小固定的条件下, 低维度矩阵的大小越接近, 其逼近高维度矩阵效果所需的有效参数就越少.

基于网络宽度评价标准的第k层剪枝系数定义为

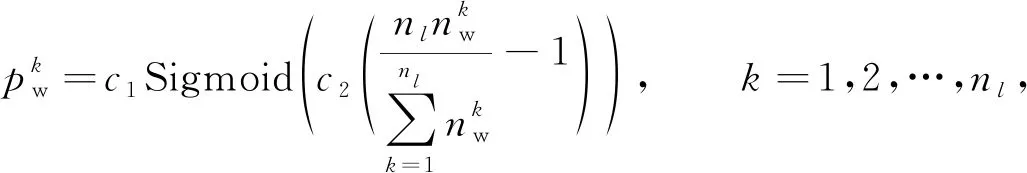
(4)

2.3 基于层的重要性评估

Han等[8]采用的基于权重的重要性评估方法目前应用广泛, 是一种很强的基线[11].在文献[8]工作的基础上, 本文充分考虑网络的层间关系, 将基于层间重要性评价标准的第k层剪枝系数定义为

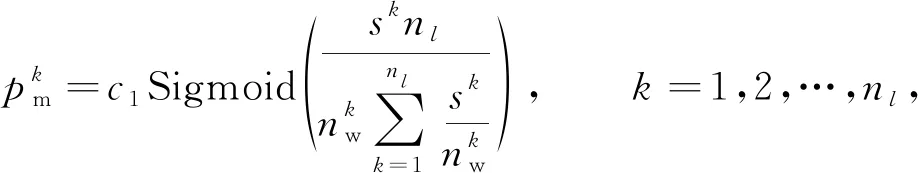
(5)

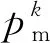
3 实 验

3.1 实验环境及参数

实验采用数据集CIFAR-10训练和测试卷积神经网络模型, 并进行剪枝效果评估. CIFAR-10 是深度学习领域常用的用于物体识别的数据集, 共有50 000张训练图片和10 000张测试图片, 这些图片共包含10个类别, 每张图片都是大小为 32×32的彩色图片.

本文实验在数据集CIFAR-10上训练了VGG-16和Resnet-20两种卷积神经网络(CNN)模型. VGG-16模型有38层, 其中16层含参数, 包括13层卷积层和3层全连接层； Resnet-20模型有20层, 除第一个卷积层和最后一个线性层, 网络中有18个卷积层, 即有9个网络模块, 可分为三段.

本文实验均训练了40个周期, 接近1.7×104个迭代循环, 采用的batch-size为128. 彩票假说的实验结果表明, 在对比剪枝率分别为0.4,0.2,0.1的情形时, 剪枝率0.2的准确率和收敛速度都表现较好, 剪枝效率远大于其他情形[12], 所以本文采用0.2作为基础剪枝率. 此外, 本文在VGG-16网络上采用0.1的学习率； 在Resnet-20网络上采用0.01的学习率. 实验环境为采用Ubuntu 16.04.7操作系统, CPU为Intel(R) Xeon(R) CPU E5-2620 v4, GPU为Tesla P40, GTX 1650Ti, 内存为32 GB, 深度学习框架采用Pytorch-1.11.0.

3.2 超参数的设置

在综合考虑网络结构的剪枝率时, 计算过程使用了超参数, 以控制剪枝率的变化幅度和在网络层间的传递速度. 本文实验中超参数的设置主要遵循以下两个原则：

1) 保证剪枝率的平均水平与基础剪枝率相同；

2) 保证剪枝率的变化幅度不超过网络的承受极限, 从而避免网络性能的急剧变化.

第一个原则表示当基础剪枝率为0.2时, 使各层的平均剪枝率尽量维持在0.2附近； 第二个原则需要保证剪枝率的变化在可控范围内, 因为剪枝率的数值很大程度影响剪枝过程的进行, 一旦剪枝率的变化幅度超过网络的承受极限, 模型的性能会急剧下降. 本文实验结果表明： 剪枝率为0.2和0.15时, 模型的拟合能力和性能趋势一致； 分层剪枝方法的性能比全局剪枝方法更好， 但当剪枝率为0.1时, 全局剪枝方法的性能反而明显优于分层剪枝方法. 因此, 当基础剪枝率为0.2时, 本文实验中控制剪枝率的变化幅度不小于0.15.

3.3 实验结果与分析

实验将NS-LPM方法与彩票实验中的全局剪枝方法、 单剪枝率的分层剪枝方法进行对比. 实验主要从压缩度(剩余权重数量)、 准确率、 训练速度三方面进行衡量. 为保证公平性, 进行多次实验, 且采用多个指标, 如最大值、 前五平均值等. 实验将各种剪枝方法应用于VGG-16和Resnet-20两种模型上.

首先, 考察网络的精确率随不同参数压缩率的变化情况. 分别将NS-LPM与单剪枝率的分层剪枝方法在VGG-16模型上的表现进行对比, 实验结果如图4所示. 其中, top-1准确率表示在训练周期内达到的最大准确率； top-5平均准确率表示在训练周期内达到的最大5次准确率的平均值. 由图4可见, 在所有剪枝方法中, 模型的精确率都会随着剪枝过程的进行先增加后降低. 在相同参数压缩率上, 基于网络结构特征的方法能达到更高的准确率, 且其在训练初期剪枝率更高, 但在训练后期剪枝率会下降. 即在训练初期, 只需要5个剪枝周期即可达到单剪枝率方法6个剪枝周期的效果. 但在训练后期(参数压缩率约达到90%), 其剪枝率会明显下降. 在各项网络特征中, 在参数压缩率达到88%前, 基于网络深度和网络宽度评价指标的准确率明显高于其他方法； 而基于层间重要性的方法更平稳, 在参数压缩率达到99%时, 表现最好.

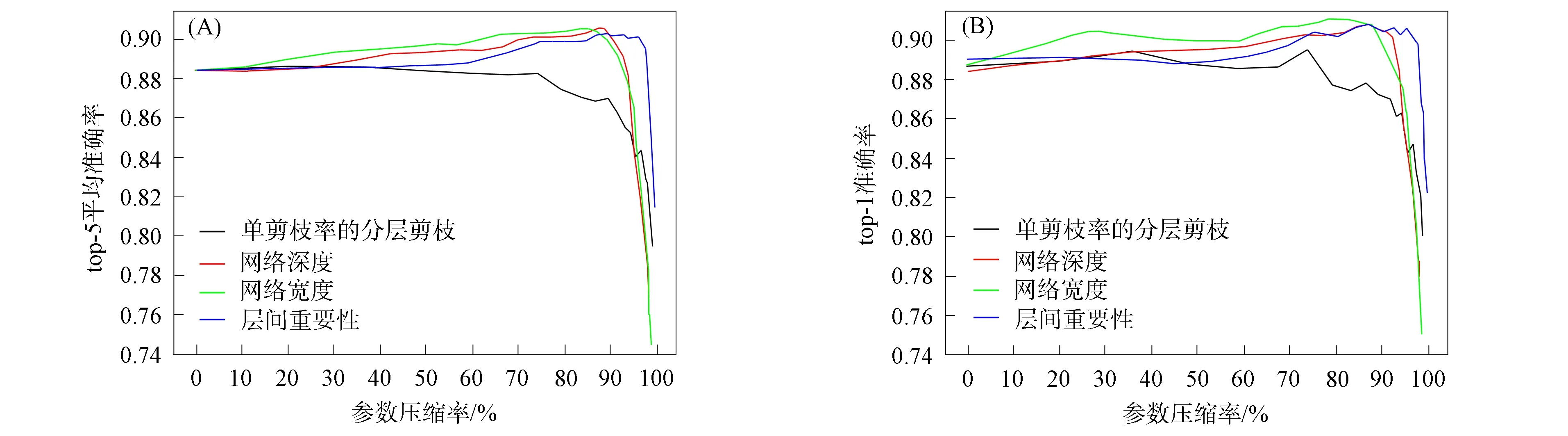
图4 基于不同网络特征的分层剪枝在VGG-16模型上的实验结果

其次, 对Resnet-20模型进行实验, 实验结果如图5所示. 由图5可见, 不同于在VGG-16模型上的表现, 在参数压缩率达到97.8%前, 基于各网络特征的方法在Resnet上的表现与采用单剪枝率的方法表现几乎一致, 尽管起点不同, 但准确率随参数压缩率的变化趋势完全相同. 但当参数压缩率达到97.8%后, 单剪枝率方法的准确率急速下降, 而基于层间重要性和网络深度的准确率更稳定. 单剪枝率方法在参数压缩率为98.86%时, 准确率为0.412； 而基于层间重要性的方法在参数压缩率为98.94%时, 准确率仍为0.618. 因此, 在VGG-16模型上, 基于网络特征的各评价方法均优于单剪枝率的评价方法； 而在Resnet-20模型上, 基于层间重要性的评价方法均优于其他分层剪枝方法.

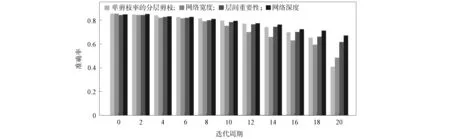
图5 基于不同网络特征的分层剪枝在Resnet-20模型上的实验结果

彩票假说实验在VGG-16和Resnet-20网络上最终采用了全局剪枝方法, 因为实验结果表明, 在大型网络上全局剪枝优于单剪枝率的剪枝方法. 这是因为全局剪枝在剪枝后期时, 不需要考虑不同层之间参数个数相差太多导致的网络结构失衡, 进而使网络不满足过度参数化的条件. 因此, 将综合所有特征后的NS-LPM方法与全局剪枝方法、 单剪枝率的分层剪枝方法进行对比, 结果如图6所示, 由图6可见, 在VGG-16模型上, 全局剪枝方法优于单剪枝率的分层剪枝方法, 其可达到更高的准确率, 同时也可达到更高的压缩率. 而在相同的训练条件下, NS-LPM方法表现良好, 甚至在压缩率和准确率上超过了全局剪枝方法.

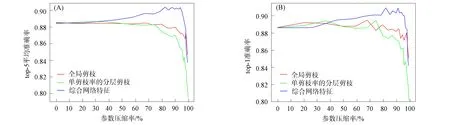
图6 基于综合网络特征的剪枝方法在VGG-16模型上的实验结果

在Resnet-20模型上的实验结果如图7所示. 由图7可见, NS-LPM方法的表现几乎不逊色全局剪枝方法， 当参数压缩率达到98.24%时, 仍能达到0.676的准确率； 分层剪枝方法在参数压缩率为98.21%时, 准确率为0.652； 而全局剪枝方法的效果最好, 在98.20%的参数压缩率时能到达0.701的准确率. 对于NS-LPM方法在VGG-16和Resnet-20模型上表现的差异, 可能是由于Resnet网络中层数过多, 使每层通道数的变化更平滑, 同时也需要考虑Resnet的残差网络及架构设计. 但相比于全局剪枝方法, NS-LPM方法在参数压缩率达到90%后, 会自适应降低剪枝率, 进而避免网络性能突然下降.

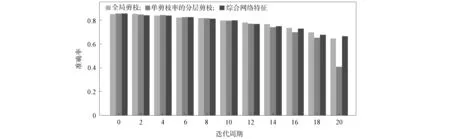
图7 基于综合网络特征的剪枝方法在Resnet-20模型上的实验结果

不同剪枝方法在VGG-16和Resnet-20模型上的实验结果列于表1. 由表1可见, 在训练初期, NS-LPM方法只需要5个剪枝周期即可达到其他剪枝方法6个剪枝周期的效果. 而且在训练后期(参数压缩率约达到90%), 其剪枝率会自适应下降. 在VGG-16模型上, 原网络使用全局剪枝方法, 压缩率达到98.85%时, 准确率达到85.0%； 使用单剪枝率的分层剪枝方法时, 压缩率达到98.85%, 准确率达到80.1%； 使用NS-LPM方法时, 进行20轮剪枝迭代可使压缩率达到99.41%, 准确度率达到83.7%, 此时其参数个数只有单剪枝率方法的51%, 而在相同压缩率时其性能甚至比全局剪枝更好. 在Resnet-20模型上, NS-LPM方法每轮的剪枝率都高于其他方法, 并且在参数压缩率达到98.94%时, 准确率仍为61.75%. 而单剪枝率的分层剪枝方法在参数压缩率达到98.85%时, 准确率只有41.2%. NS-LPM方法的表现在Resnet-20模型上已经接近全局剪枝方法.

表1 不同剪枝方法在VGG-16和Resnet-20模型上的实验结果对比

综上所述, 针对传统分层剪枝方法在剪枝过程后期时, 网络模型的准确率会随网络结构失衡陡然下降的问题, 本文提出了一种基于网络结构的分层剪枝方法NS-IPM, 其在进行剪枝时, 创新性地结合了网络结构的特征信息. 不同于传统的分层剪枝方法, NS-IPM方法通过对网络深度、 网络层宽和层间重要性评估综合考虑, 构建复合评分确定每层的动态剪枝率. 本文将单剪枝率的剪枝方法、 全局剪枝方法与NS-IPM方法进行对比, 证明了NS-IPM方法的有效性, 并讨论了不同的剪枝率变化方法对网络性能的影响. 基于网络结构的分层剪枝方法NS-IPM在主流的VGG和Resnet网络模型上都表现良好, 显著改善了传统分层剪枝方法在大型网络模型上使用受限的情况, 与传统剪枝方法相比优势明显.