二维蜂窝弹性材料拓扑态的研究*

李荫铭，孔 鹏，毕仁贵，何兆剑，邓 科

(吉首大学物理与机电工程学院，湖南 吉首 416000)

近几十年来，随着拓扑绝缘体[1-4]概念的提出，新奇的物理效应使得其成为凝聚态物理备受关注的热点课题.在电子系统中，人们已经发现了描述波函数在相关色散带上的量子化行为的拓扑特性[5].受到电子系统中拓扑相关概念的启发，研究人员通过类比经典体系和量子体系，发现体态拓扑相分类和相应的拓扑表面态(或边界态)也存在于光子晶体、声子晶体等人工晶体中，其更加容易制备的优势使得在经典波中实现拓扑效应成为研究热点[5-9].近年来，人们在探索光子晶体及声子晶体的拓扑性质中，出现了许多有趣的现象，如单向传输、定向无衍射传输等[10-13]，这为操纵声波、电磁波寻找到更多新的自由度.

在声学系统实现拓扑效应的研究中，最早出现的是通过打破体系的时间反演对称性，从而实现声量子霍尔效应，但此实现方式往往需要引入外部场，如引入循环流体等[2].随后有学者提出了声学量子自旋霍尔效应，理论的提出已成功证明了在时间反演不变中系统也能实现声学拓扑效应[14]，相较于之前研究需要打破时间反演对称性，这无疑是提供了一种更为简单的解决方案.2016年，Lu等[15]利用打破镜面对称性的方法实现了量子谷霍尔效应，提出了声学谷态的概念，这也是在声学系统中实现拓扑态最简单的一种办法.目前，大部分研究较多关注在流体介质中实现声学拓扑态，而固体材料中弹性波的拓扑性质相关研究却相对较少，这是由于声波在固体材料中是以横向极化和纵向极化两种模式共同存在，在弹性波中寻找拓扑态，用于实现类似于空气声中的边界输运、选择性激发等还存在一定困难，不过这也意味着此研究方向蕴含更大的研究空间.

笔者基于弹性材料设计了二维蜂窝声子晶体，在多频段实现了SV模式波的多个狄拉克简并点.当相邻两个六边形完全相同时，整个体系受时间反演和空间反演对称性的保护，在布里渊区角点处出现3个线性简并的狄拉克点，分别对应在不同的频段中.通过调整蜂窝晶格的几何结构，破坏体系的空间对称性，使其在K(K′)点处的多个狄拉克点同时打开，在多个频段形成谷态.

1 二维弹性声子晶体的设计

使用细长管道将相邻的六边形A和B两两连接起来，组成规则的蜂窝六角晶格声子晶体，见图1.红色实线包围的是单胞结构，该声子晶体的晶格常数a=4 mm，其中六边形A和B的晶格常数用a1、a2表示，均为0.55 mm，连接通道的宽度b=0.2 mm.使用不锈钢作为整个模型的材料，参数如下：弹性模量E=210.6 GPa，剪切模量μ=81 GPa，质量密度ρ=7 780 kg/m3.

图1 声子晶体的几何结构

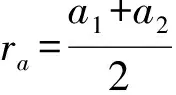
图2 声子晶体的能带结构

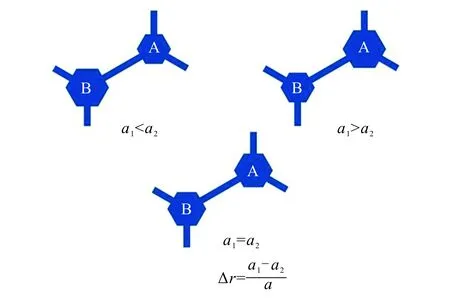
图3 不同的微扰参数Δr对应的单胞结构

2 体模态的涡旋场及拓扑性质分析

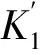
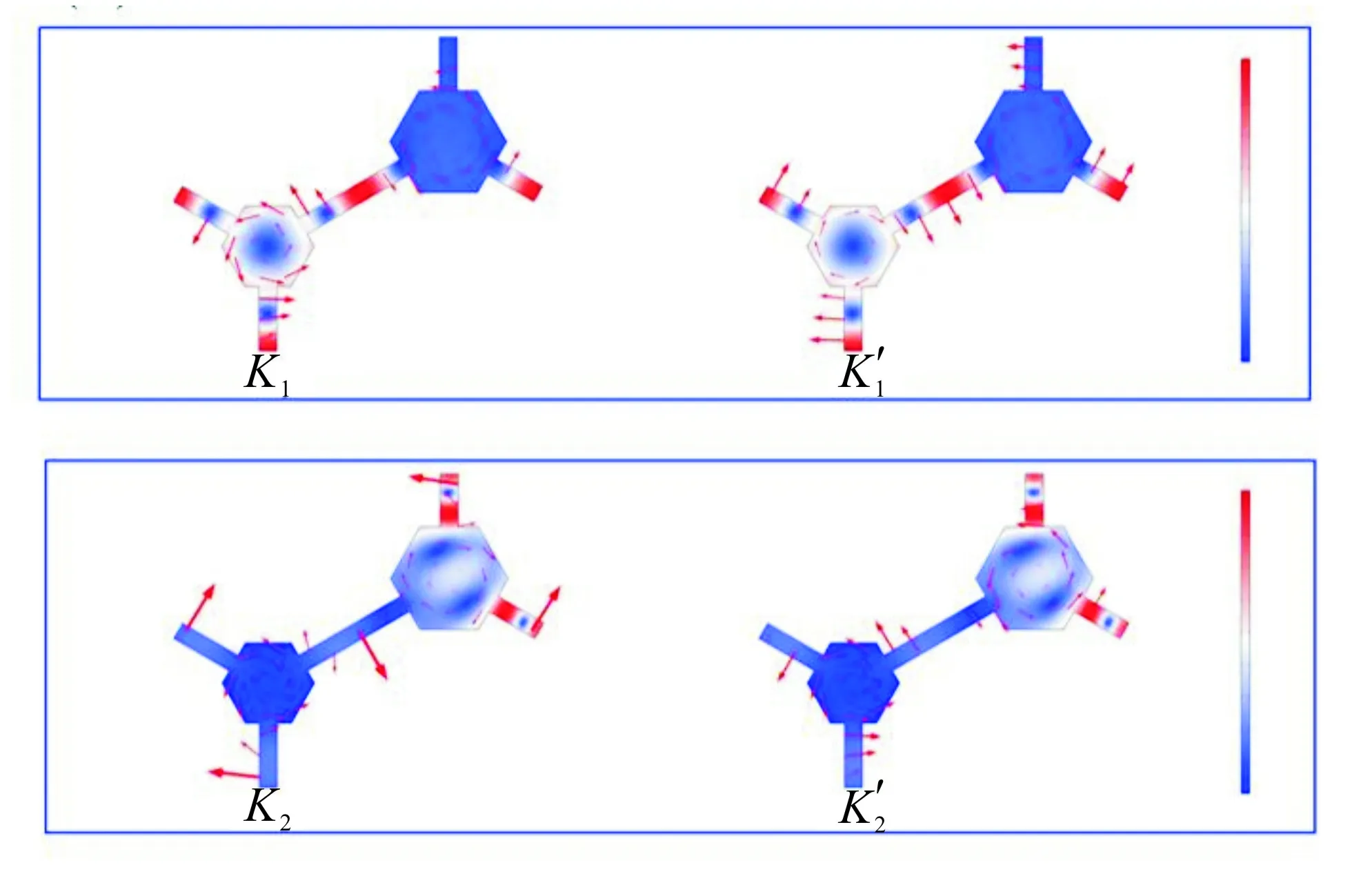
图4 体模态的涡旋场和拓扑相变

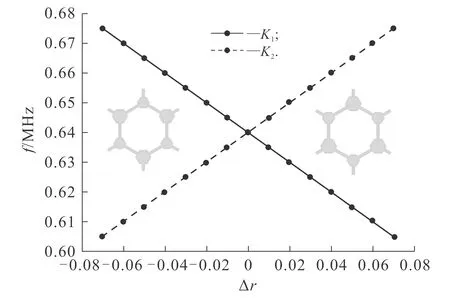
图5 能带反转时上、下能谷频率随Δr的变化

HK=vD(δkxσx+δkyσy)+Δgσz，

(1)

其中：vD是狄拉克点附近的有效群速度；δkx和δky则分别表示动量空间中波矢在K点附近的偏移量；σi是泡利矩阵.当Δr=0.06时，上、下能谷之间的带隙频率可以表示为Δg=f+-f-，对于较低一条带，贝利曲率

(2)

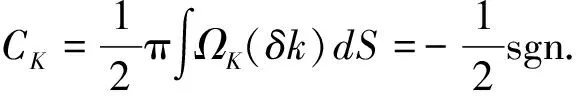
3 总结

笔者基于弹性材料设计了二维蜂窝声子晶体，在系统具有C3v对称性时，在布里渊区角点处K(K′)点出现了3个线性简并的狄拉克点.引入微扰参数打破体系的空间对称性，使得原本出现的狄拉克点打开，带隙形成能谷.并通过对低频段的上、下能谷的体模态涡旋场进行数值模拟分析，发现该声子晶体随着结构参数的改变发生了拓扑相变，同时揭示了谷态出现的原因.最后利用k·p微扰理论对其在两种微扰参数下能谷的拓扑荷进行分析，发现其具有非零的谷陈数.