基于GSA-RGMM的多模态热工过程故障监测与诊断

蒲健飞，任少君，周东阳，曹 军，范 伟，司风琪

(1.东南大学 能源热转换及过程测控教育部重点实验室，南京 210096；2.西安热工研究院有限公司，西安 710054)

随着信息化的发展，火电机组自动化程度越来越高，对电站设备的安全性和可靠性提出了更高的要求。基于数据驱动的故障监测与诊断方法具有数据代表性好和方法通用性强等优点，受到了学术界和工业界的广泛关注。基于数据驱动的故障监测和诊断方法主要分为两类：一类是基于有标签数据的有监督方法，如人工神经网络(ANN)[1]、支持向量机(SVM)[2]等；另一类是基于无标签数据的无监督方法，如多元统计方法(MSPM)[3]和高斯混合模型(GMM)[4]等。有监督故障诊断方法对于难以获得大量故障工况样本的过程具有较大的局限性，并且对未知故障类型诊断能力差；无监督故障诊断方法通过设备正常运行数据建立故障监测模型并计算故障限值，当统计指标超过限值时进行故障预警。无监督故障诊断方法因具有通用性强、建模样本易获得等优点在工业领域得到了广泛的使用。

无监督故障诊断方法中基于MSPM的故障诊断算法(如主成分分析(PCA)[5]、偏最小二乘(PLS)算法[6])通过计算故障监测指标平方预测误差Q和T平方(T2)进行故障监测，需要设备运行数据服从高斯分布才能保证监测的限值的有效性[7]。在实际热工过程中，随着负荷的变化，设备运行模态(工况)随之发生变化，使得设备运行数据呈高斯混合分布。针对运行数据呈高斯混合分布的多模态过程[8]，GE Z Q等[9]通过模糊C均值算法对训练样本进行分割并建立多个子模型对多模态过程进行监测，该方法在线监测时计算量大，降低了在线监测效果。YU J等[10]提出一种基于GMM的多模态过程故障监测方法，并通过基于概率的全局贝叶斯推理作为监测指标进行故障监测，但传统GMM受初始参数的影响容易陷入局部最优解。YANG M S等[11]通过在期望最大化(EM)算法目标函数中加入信息熵的方式提出鲁棒高斯混合模型(RGMM)算法，实现了高斯成分数的自适应更新，避免模型参数陷入局部最优。当监测到故障发生时需要进一步进行故障变量定位，传统贡献图通过计算故障统计量贡献进行故障分离，由于拖尾效应[12]的影响，造成分离结果误诊率高。

针对历史数据呈高斯混合分布的多模态热工过程，笔者提出一种融合监测指标的引力搜索算法(GSA)[13]故障分离方法。首先，使用RGMM算法建立故障监测模型，监测到故障后计算故障样本各变量的贡献；其次，利用融合监测指标的GSA对潜在故障变量进行故障重构；最后，确定样本中的故障变量。分别采用多模态数学算例和高压加热器(简称高加)作为研究对象，验证该算法在多模态热工过程的故障监测和诊断中的有效性。

1 RGMM算法

设原始数据集X∈Rm×n(R为实数组成的矩阵)为C个模态的测量数据，X=[x1,x2,…,xm]，其中：C为GMM成分数；m为样本数量；n为变量数量；x为任意时刻观测值。其概率密度函数p(x|θ)可以表示为：

(1)

第k个高斯成分的密度函数为：

(2)

式(2)中模型参数通过EM算法[14]进行迭代求解。

根据贝叶斯理论计算隐变量的过程如下。

(3)

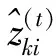
调整系数β(0≤β≤1)可以定义为：

(4)

然后更新模型参数，即

(5)

(6)

(7)

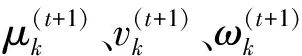
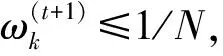
(8)

(9)

RGMM算法计算流程见表1。

表1 RGMM算法计算流程

2 基于GSA-RGMM的故障监测与诊断

2.1 故障监测

当设备发生故障时需要及时进行故障预警，防止故障进一步恶化。针对多模态过程，建立基于RGMM的故障监测模型并通过故障监测指标GBID和GBIP进行故障预警。

定义样本点x对于第k个高斯成分的修正马氏距离Dr为：

Dr[(x,Ck)|x∈Ck]=

(x-μk)T(vk+φI)-1(x-μk)

(10)

式中：φ为极小值，用于去除协方差矩阵的奇异性；I为单位矩阵。

样本x属于第k个高斯成分的后验概率P(Ck|x)为：

(11)

全局监测指标GBIP定义为：

Dr[(x,Ck)|x∈Ck]}

(12)

选取置信度为γ，当GBIP>γ时，认为设备发生故障，反之，认为设备运行正常[10]。

基于局部马氏距离的全局监测指标[15]GBID为：

(13)

GBID指标的限值L根据F分布[16]计算，计算公式为：

企业对于IPO的困惑，宋彬也给予了解读。“新三板企业IPO始于2007年，受企业资质和IPO暂缓等因素的影响，历年IPO数量分布不均。2016年前，新三板企业IPO数量较少，2017年以来，已成功IPO的新三板企业数量激增，其中2018年已达18家。”从新三板企业IPO情况来看，截至2018年9月30日，已有55家新三板企业成功过会，其中已有48家成功登陆A股市场。“新三板企业IPO板块中，目前55家已过会的新三板企业中，有28家选择登陆创业板，9家选择登陆中小板，18家选择登陆主板，符合新三板企业‘小而精’的总体特征。”

(14)

式中：L为置信度为γ时的GBID指标的限值；γ的取值通常为95%和99%；n和p分别代表样本数量和变量数。当GBID≥L认为设备发生故障，反之则运行正常。

2.2 基于GSA的故障分离方法

当故障监测指标超过限值时，表明设备发生故障，需要进一步进行故障分离，分离出故障发生的参数，定位故障变量。

基于重构的故障分离方法为根据故障变量通过测量值x找出对应的正常值x*，即单故障时为x*=x-s(p)fp，多故障时为x*=x-s(p)fp-s(q)fq。其中：s(p)、s(q)为故障变量；fp、fq分别为s(p)、s(q)对应的故障幅值。基于GSA重构的故障分离方法是通过找出故障变量和对应的故障幅值使故障监测指标达到最小值。

以GBID监测指标为例：

Dr[(x-sf),Ck]}

(15)

当GBID降到控制限以下时，表明s为真正的故障变量，f为对应的故障幅值。

GSA是一种源于万有引力定律的启发式智能优化算法,通过粒子位置的移动搜索空间中的最优位置，获得优化问题的最优解，GSA具有收敛速度快、全局搜索能力强的优点[13]。

将故障重构转化为最优解问题，选取重构故障变量集，当minGBID小于限值时，证明该变量集为故障变量，反之，证明该变量集并非真实的故障变量。

表2 基于GSA-RGMM算法故障重构流程

2.3 基于高斯混合贡献的重构变量选取

通过重构的方式进行故障分离需要先预设故障变量，再对故障变量进行重构实现故障分离，随着维度的升高，变量组合会呈指数增长，计算量较大。为此，采用组合优化的思想是将故障变量逐个定位出来，计算出故障样本在各变量的高斯混合贡献，选取高斯混合贡献最大的变量加入重构变量集，如果重构监测指标低于故障限值，则重构变量集即为真实故障变量，否则根据重构后的样本更新高斯混合贡献，选取其中贡献最大的变量加入重构变量集，直至重构监测指标低于故障限值，输出真实故障变量。

式(10)可以改写为：

Dr[(x,Ck)|x∈Ck]=

(16)

(17)

(18)

图1 基于GSA-RGMM算法的故障监测与诊断流程

3 数学算例分析验证

为验证提出的故障监测与分离方法的有效性，建立如下数值案例[10]：

(19)

式中：[e1,e2,e3]T为均值为0、方差为0.01的白噪声；[s1,s2]T为服从高斯分布的数据源。

在数据源中设置如下3种分布状态，分别表示不同的操作模态。

(1)分布1：s1=N(5,0.6);s2=N(20,0.7)。

(2)分布2：s1=N(10,0.8);s2=N(12,1.3)。

(3)分布3：s1=N(16,1.5);s2=N(30,2.5)。

由式(19)生成3 000组正常运行的数据作为训练数据，其中3个模态各占1 000组，见图2。

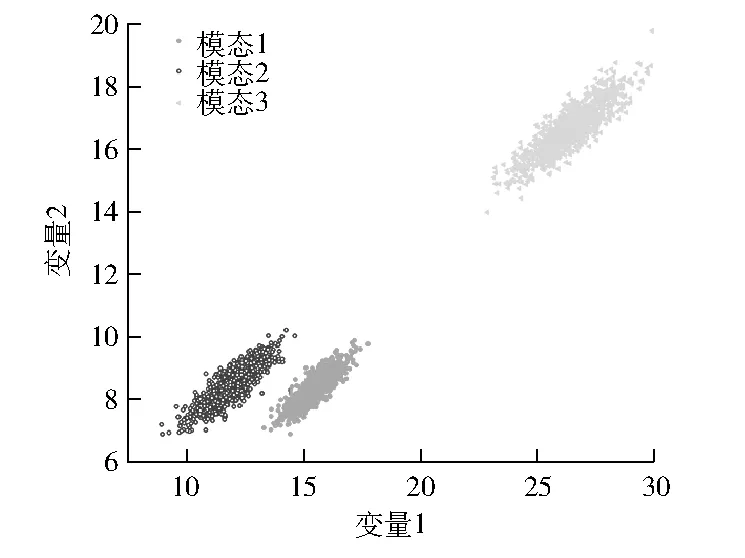
图2 多模态仿真数据

故障模拟形式为：

xfault=x*+f

(20)

由式(19)生成正常工况样本，并通过式(20)的方式进行故障仿真。

故障1：取500组模态1数据，归一化后从第100组样本开始，在变量1上加入幅值为0.3～0.5的偏差。

故障2：取500组模态2数据，归一化后从第100组样本开始，在变量2上加入幅值为0.004(k-100)的偏差，其中k为样本序号。

故障3：随机选取500组3个模态数据，归一化后从第100组样本开始随机选择2个变量分别加入幅值为0.8～1.0的偏差。

通过正常工况样本训练RGMM并通过GBIP和GBID对故障仿真数据进行监测。为证明RGMM算法的有效性，采用GMM算法和PCA算法对故障仿真数据进行监测，并与RGMM算法进行对比，结果见表3。

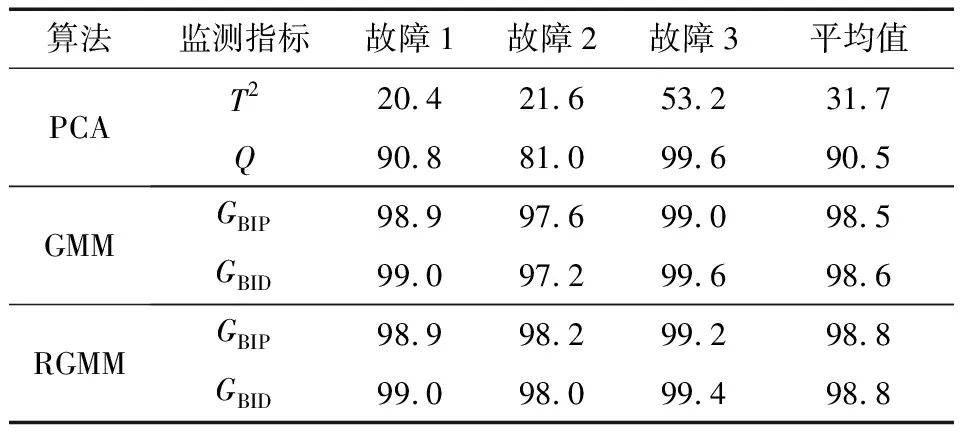
表3 故障监测准确率 %

由表3可以看出：在多模态过程中当故障幅度较小时，RGMM算法相比于PCA和GMM算法具有更强的敏感性，监测准确率更高。

当监测到故障后还需要进一步通过故障分离方法定位故障变量，判断故障类型。采用故障诊出率(FDR)和故障误诊率(FAR)这两个评价指标对诊断结果进行评价[17]。有效的故障分离算法具有较高的故障诊出率和较低的故障误诊率。

为验证提出的故障分离算法效果，将所提方法与传统贡献图(CP-PCA)、重构PCA(RB-PCA)和GMM算法的结果进行对比，结果见表4。在多模态过程中由于PCA算法的故障监测准确率较低，导致其故障诊出率低于GSA-RGMM算法。当故障幅度增加时，受残差污染的影响，CP-PCA和GMM算法误诊率高于GSA-RGMM算法，表明基于重构的 GSA-RGMM算法能有效降低故障误诊率。

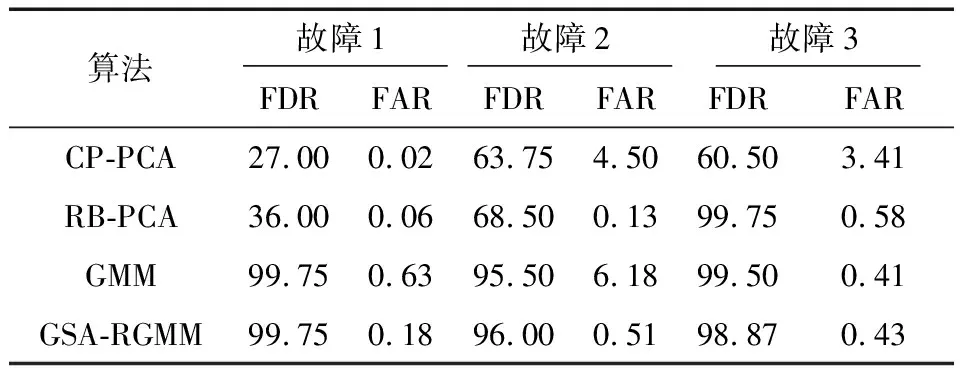
表4 故障分离结果 %

4 高加故障诊断

高加作为火电机组回热系统的重要组成部分，对保障火电机组的安全经济运行具有重要作用。高加长期运行于高温、高压和变工况环境中，容易发生管路泄漏和积垢等故障，影响机组安全稳定运行。以某660 MW燃煤机组1号高加作为研究对象,采集2020年6月29日—7月4日高加相关测点数据(见图3)。由图3可以看出：受调峰影响，机组负荷呈白天高、夜晚低的趋势，并且高加运行参数与负荷具有较强的相关性。

图3 1号高加运行数据

1号高加运行参数概率密度分布见图4。

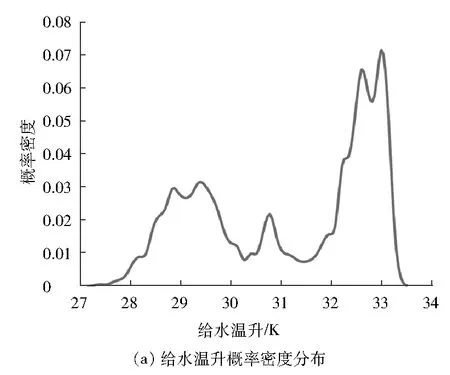
图4 1号高加运行参数概率密度分布

由图4可以看出：高加运行参数呈高斯混合分布。采用稳态筛选算法[18]提取2 000组稳态运行数据建立基于RGMM、GMM和PCA算法的高加监测模型。为验证算法多模态过程中的故障监测与分离的有效性，采用分段热力计算方法建立高加故障仿真模型[19],该仿真模型涉及9个变量，分别为6个输入变量(tsin、twin、pwin、h、pst、qmw)和3个输出变量(Δt、θ、Dod)，具体描述见表5。

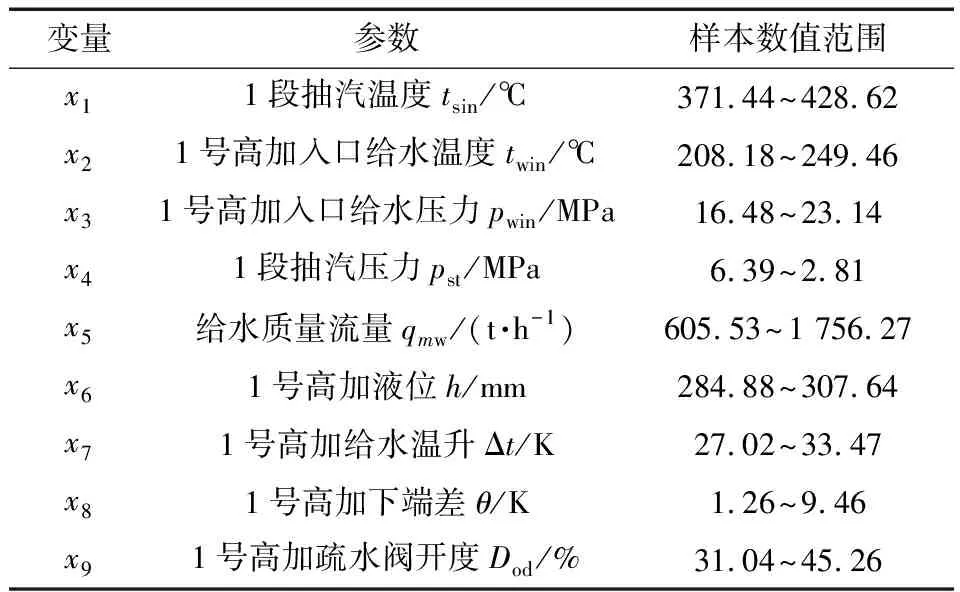
表5 1号高加仿真模型变量名称及范围

选取800组稳态样本作为测试样本，并在201组样本点处加入表6中所列故障。根据故障仿真结果和文献[19]中的故障特征分析，得出模型故障类型与对应故障参数(见表6)。

表6 1号高加故障列表

通过不同监测模型得到高加故障的监测准确率，结果见表7。

表7 故障监测准确率 %

图5和图6分别为故障d、故障e监测结果图。由图5和图6可以看出：RGMM算法相对于PCA算法和GMM算法具有更高的准确率。在高加建模过程中，RGMM算法在处理分布复杂的热工过程数据时相比于GMM算法具有更强的鲁棒性，并且模型精度更高。

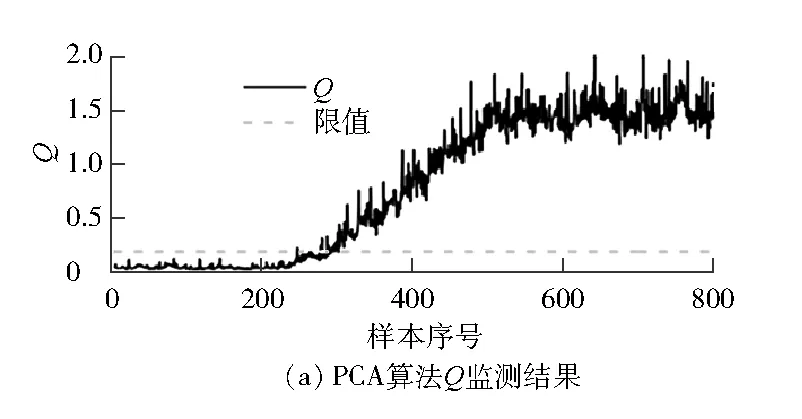
图5 故障d的故障监测结果

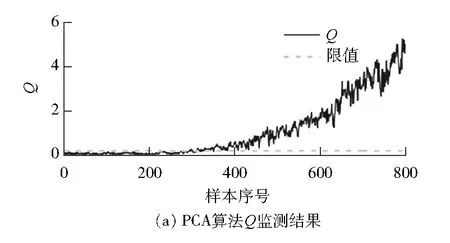
图6 故障e的故障监测结果

监测到故障后再通过提出的GSA-RGMM算法进行故障分离，同时与基于PCA算法的CP-PCA、RB-PCA和GMM算法进行对比，故障分离效果比较见表8，图7和图8分别为故障d、故障e的故障分离结果，所提算法具有更高的故障诊出率和较低的故障误诊率。

表8 故障分离结果 %

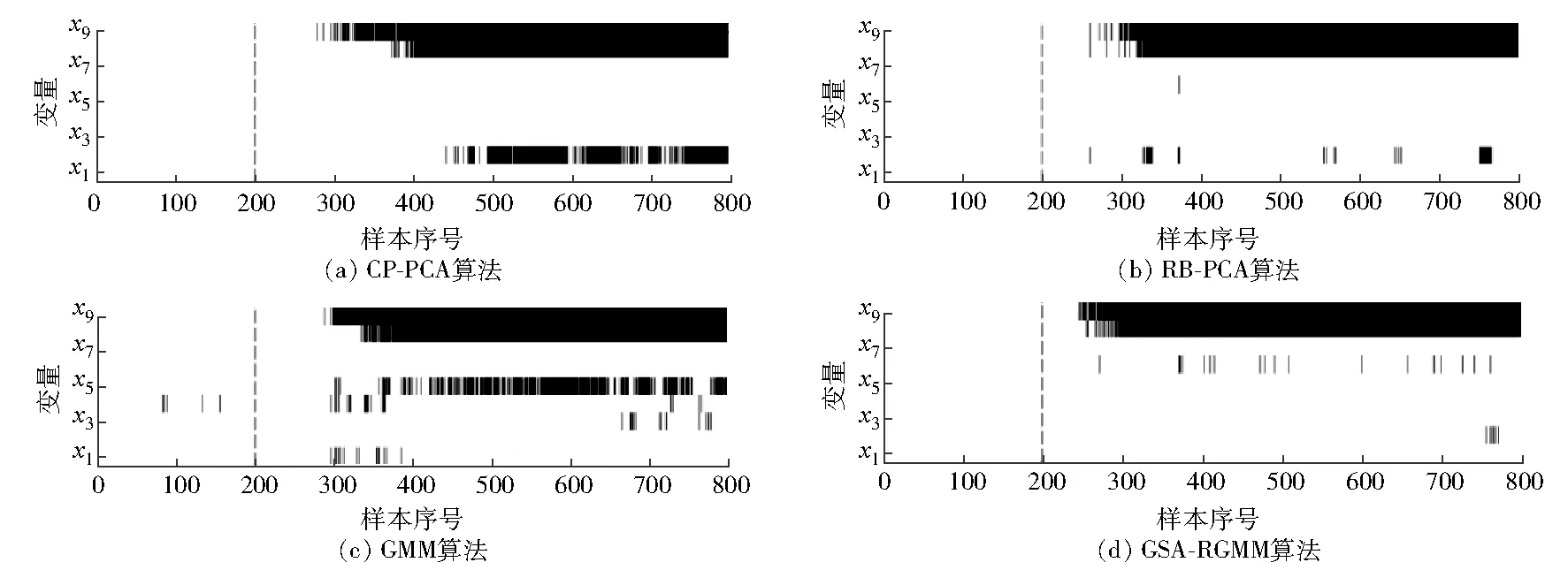
图7 故障d故障分离结果

图8 故障e故障分离结果

5 结语

为提高多模态热工过程故障监测与诊断准确性，采用RGMM算法建立故障监测模型，并使用两个故障监测指标(GBIP和GBID)进行实时故障监测，当故障指标超过限值时表明设备发生了故障。提出GSA-RGMM算法分离相关故障参数。该方法先通过高斯混合贡献法计算故障样本各变量的高斯混合贡献，根据贡献大小逐步选择变量加入重构变量集，直至基于GSA算法重构的监测指标低于故障限值，输出故障变量，完成故障分离。

以多模态数值算例和某燃煤机组1号高加为研究对象，验证该算法的有效性，结果表明：相比于PCA算法和传统GMM算法，RGMM算法具有较高的故障监测准确率；同时，相比于CP-PCA、RB-PCA和GMM算法，GSA-RGMM算法能准确分离出故障变量，具有较高的故障诊出率和较低的故障误诊率，表明该算法在多模态热工过程故障监测与诊断中的有效性和可行性。