基于自适应阈值分割的电力变压器呼吸器变色检测方法

施润杰

（济宁学院产业学院，山东 济宁 273199）

0 引言

电力变压器作为变电站的重要设备，一旦发生故障将会对电力系统的正常运行产生非常严重的影响[1]。呼吸器作为净化变压器吸入空气的重要设备，可以有效过滤空气中的水分来达到减少变压器油的受潮和氧化的效果。如果呼吸器因吸附水分饱和而变色失效，极易造成变压器油受潮，导致变压器油的绝缘强度下降，存在引发变压器内部故障的风险。因此，及时发现和更换失效的呼吸器硅胶，对保证变压器正常运行至关重要[2]。

针对呼吸器变色失效问题，目前主要依赖于人工巡视[3]。但由于操作员的疲劳、疏忽等主观因素，该方式会导致维护效率低下及效果不佳，同时该方式无法与智能巡视机器人等自动化设备对接以实现智能巡检[4]。目前的解决方案存在成本高等问题，无法在短期内大量部署。因此，当前呼吸器变色检测技术急需通过一种低成本、高效率的算法解决上述问题。

目前变压器呼吸器变色检测研究大多都是基于计算机视觉的方式进行，该检测方法具有避免破坏现场生产环境、降低投入成本，便于智能巡视等优势。例如，文献[5]使用同态滤波对待检测图片进行预处理，之后在HSV（Hue-Saturation-Value）颜色空间使用颜色直方图的方式对H、S两分量进行颜色统计，并以此为根据进行决策判断。由于变压器呼吸器一般存在于室外且外侧为透明玻璃材质，受拍摄角度和环境光照等因素影响，图像会产生不同程度的高反射区域，导致同态滤波和直方图统计法失效，检测效果差，因此该方法只能针对特定的使用场景；文献[6]通过采集不同时段的样本，人工总结出HSV先验阈值，之后利用这些先验阈值对颜色进行提取，根据颜色占比对该呼吸器变色程度进行判断。该算法在实际使用由于存在人工影响，因此阈值不具有自适应性；同时，现有检测方式都是通过对硅胶颗粒像素点的统计来计算呼吸器变色程度的，不符合呼吸器的变色规律。

为解决上述问题，文中提出了一种基于多尺度Retinex和自适应阈值分割的呼吸器变色检测方法。通过多尺度Retinex算法，使原始图像色彩对比度增加，抑制高反射区域的影响；通过提出自适应阈值分割算法，使得颜色分割阈值不依赖于先验知识，增强算法的适用性和鲁棒性；通过对硅胶颗粒区域的分割，基于变色面积对呼吸器变色程度进行判断。

1 呼吸器变色检测算法流程

文中所提出的呼吸器变色检测算法的流程图如图1所示，具体步骤如下。

图1 呼吸器变色检测算法的流程图

1）输入图像。

输入巡检机器人现场拍摄并传回的呼吸器图片。

2）图像预处理。

使用多尺度Retinex算法对待检测图像进行预处理。消除高反射对图像的影响，增强色彩之间的对比度。

3）硅胶颗粒区域提取。

a）将预处理后的图像转换至HSV颜色空间；

b）将H通道作为主色彩通道进行中值滤波处理，消除椒盐噪点；

c）使用HSV三通道信息对H通道进行二值化处理，得到硅胶颗粒区域的大概位置；

d）通过开运算去除较小非目标区域，并圆滑目标区域边缘；

e）使用最大连通域搜索算法，消除较大非目标区域，得到硅胶颗粒区域的最终位置；

f）通过与运算，得到硅胶颗粒区域对应的H通道数据。

4）硅胶颗粒区域分割。

a）对步骤2中提取到的硅胶颗粒区域对应的H通道数据，分别计算其每列的阈值；

b）对每列H通道的阈值进行拟合，得到两色分割线。

5）变色决策判断。

使用分割线将硅胶颗粒区域分割为两部分，分别判断两部分颜色及两部分面积，继而判断呼吸器变色程度。

2 图像预处理

Retinex理论即视网膜大脑皮层理论，由Land等人于20世纪60年代提出，是一种基于人类视觉感知的色彩理论[7]。该理论包括以下两方面内容：1）物体表现出的颜色主要由物体的反射性质决定，不受光照的影响；2）自然界中所有物体的颜色具有恒常性，不受光照非均匀性的影响，光照不均不会影响物体颜色的一致性[8]。Retinex理论的思想是减少甚至消除光照图像对视觉效果的影响，保留反映图像本质属性的反射图像，从而达到图像增强的目的。

根据Retinex理论，一幅图像I（x，y）可以由光照分量L（x，y）和反射分量R（x，y）乘积得到，其数学表达式如下所示：

其中：光照分量L（x，y）起着决定图像动态范围的作用；反射分量R（x，y）则对应图像细节纹理信息。

在处理时，为了方便对光照分量和反射分量的分离，以及更符合人的视觉系统以及相机对光的感知[9]，通常将式（1）转至对数域，把乘积的关系转化成为和的关系，即：

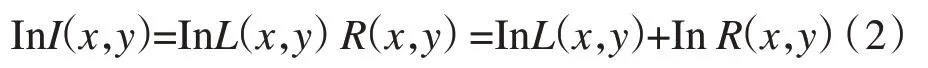
当光照分量可以表示为图像与高斯滤波函数的卷积时，反射分量可表示为：

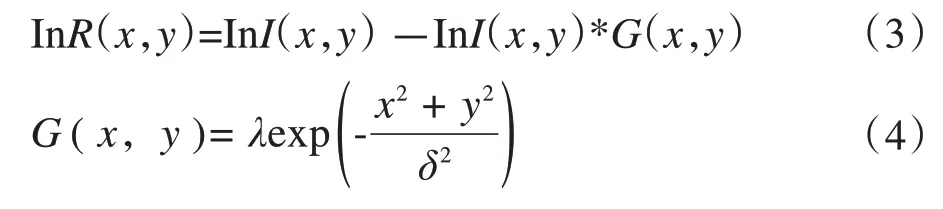
其中：*表示卷积运算；G（x，y）为高斯滤波函数；λ为满足时的归一化常数；δ为环绕参数，一般也称为尺度参数。

式（3）又被 称 为单尺 度Retinex算 法（Single Scale Retinex，SSR）[10]。由于SSR只有单一的参数δ，该算法不能同时兼顾动态范围压缩和色感一致性[11]。为解决这一问题，Rahman等人提出了多尺度Retinex算法（Multi-Scale Retinex，MSR）[12]，其主要思想是对多个具有不同方差的高斯滤波函数的SSR结果进行加权平均，即：

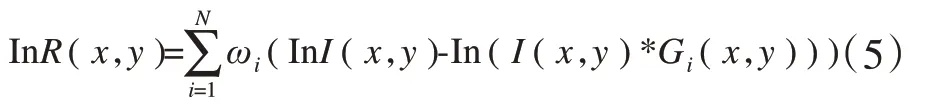
其中：N是环绕尺度数量；ωi是不同尺度的权值，且满足通常情况下，N=3，即MSR算法对图像采用大、中、小3个尺度进行加权平均。

3 硅胶颗粒区域提取

3.1 HSV颜色空间

HSV颜色模型是指用颜色的基本属性色调（Hue，H）、饱和度（Saturation，S）和明亮度（Value V）来表示色彩。与面向显示设备的加色混色（Red-Green-Blue，RGB）模型相比，HSV颜色模型能更好地反映人对色彩的感知，适用于面向视觉的分析处理[13-14]。HSV颜色模型与RGB颜色模型的转化关系如式（6）、式（7）和式（8）所示：

其中：H、S、V分别表征颜色的色调、饱和度和明亮度；R、G、B分别为RGB空间中像素通道值；H′为转换过程中色调的中间值；Tmax、Tmin分别为R、G、B中的最大值和最小值。

3.2 中值滤波

在获取图像的过程中，由于环境、成像设备、人为等因素的影响导致较易于产生噪声。根据概率密度函数分类，图像噪声可以分成伽马噪声、高斯噪声、椒盐噪声等，其中椒盐噪声和高斯噪声是图像处理中最常遇到的两种噪声[15]。因此在图像处理过程中，需要对图像进行滤波去噪。常用滤波算法有均值滤波[16]，高斯滤波[17]和中值滤波算法[18-19]。均值滤波器原理简单，运行速度快，但是对椒盐噪声效果较差，并且在去噪的同时破坏了图像细节；高斯滤波器是一种线性非平均滤波器，其对于高频噪声的抑制效果较为明显，但同时细节纹理部分也被模糊了，并且不能有效消除椒盐噪声；中值滤波器可以有效的消除图像中的椒盐噪声，并且保证图像细节不被破坏，缺点是不能有效抑制高斯噪声，且如果椒盐噪声过多图像会产生孔洞。通过测试发现，图像H通道存在的噪声多数为椒盐噪声，且噪声程度偏低，因此文中使用中值滤波器进行图像去噪。其基本原理如式（9）所示：

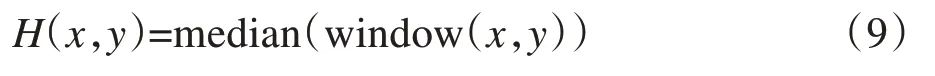
其中：H（x，y）表示图像H通道在像素点（x，y）处的H值；window（x，y）表示以像素点（x，y）为中心的窗口函数，窗口大小N=2*k+1，K=1，2，3…；；median（.）表示取中值函数。

3.3 硅胶颗粒区域预提取

由于已知HSV三通道数值与标准色彩之间的对应关系，如表1所示，以及硅胶颗粒颜色变化范围为红色、蓝色和紫色，并且H通道中图片背景区域数值与硅胶颗粒区域数值差异较大。因此文中利用HSV三通道的信息对H通道进行二值化处理，并使用红色、蓝色和紫色对应的HSV三通道数值范围作为阈值，实现对硅胶颗粒区域的预提取。计算公式如下式所示：

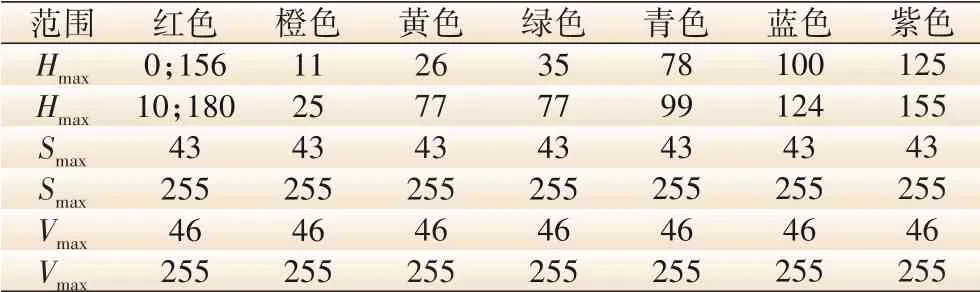
表1 HSV颜色对照表

其中：H(x，y)、S(x，y)、V(x，y)分别表示HSV图像在像素点(x，y)处的色调、饱和度和明亮度；Hr1max表示红色H通道的最大值（第一部分）；Hbmin表示蓝色H通道的最小值（第二部分）；Sbmin、Sbmax分别表示蓝色S通道的最小值和最大值；Vbmin、Vbmax分别表示蓝色V通道的最小值和最大值。

3.4 形态学开运算

开运算由腐蚀运算和膨胀运算构成，计算公式如式（12）所示[20]。

其中：⊗表示开运算；Θ表示腐蚀运算；⊕表示膨胀运算；A、B为两幅图像，A为被处理对象，B为结构元素。

4 硅胶颗粒区域分割

4.1 H通道自适应阈值计算

由于硅胶颗粒的变色过程是一个渐变过程，总是从上至下或者是从下至上，两种颜色分界线并不是那么明显，同时由于不同人对颜色的认知会有些许差别，每个人有不同的标准，这就会引入观测误差。因此文中提出了一种自适应划定两种颜色分界线的算法。该算法基于以下两点假设：

1）待识别呼吸器变色过程的发生方向总是沿竖直方向或接近竖直方向。

2）呼吸器中硅胶颗粒总是处于圆柱形容器中，且变色平面与圆柱形容器上下底面平行或接近平行。

只有假设1成立的前提下我们才能判断呼吸器变色发生是自上而下还是自下而上，进而判断呼吸器变色发生的原因。假设2指出硅胶颗粒的变色过程是连续的，均匀的，保证两颜色之间的分界线是可导的，分界线可用一般初等函数合成表示。

给定=[x1，x2，x3，…，xn]为待分类一维向量，将x→分为两部分构造fscore（i）函数，分子使用 的两部分均值的二范式平方表示类间距离，分母使用的两部分分别与各部分的均值的二范式平方和表示两部分的类内距离。通过最大化类间距离和最小化类内距离来实现最优分割位置的自动获取[21-22]。H通道自适应阈值计算算法原理如式（13）、式（14）：

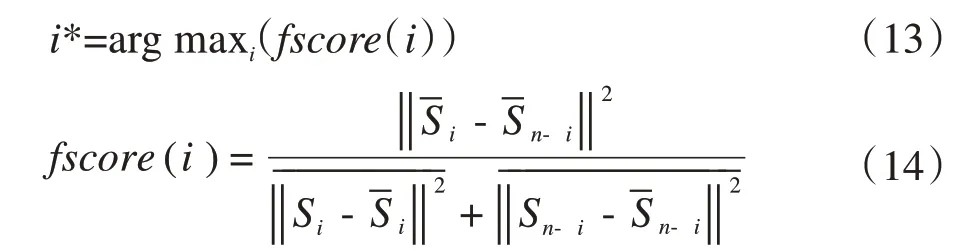
其中：i表示的索引位置；i*表示最优分割位置；Si表示的前i个元素组成的子向量；Sn-i表示的后n－1个元素组成的子向量分别表示Si和Sn-i的平均值。

4.2 H通道自适应阈值拟合

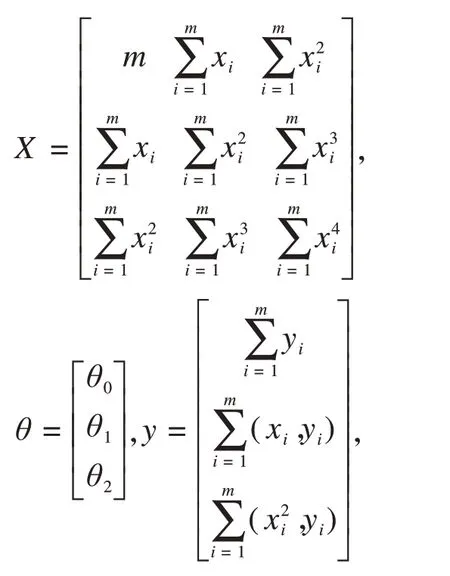
未处理的自适应阈值会带有毛刺，还无法直接进行硅胶颗粒面积计算。基于上节中的假设2，我们对分割结果进行拟合，通过实验发现分割点分布基本服从二次函数f(x)=θ0+θ1x+θ2x2。利用最小二乘法对该函数进行拟合[23]，即：

其中：

5 呼吸器变色决策判断

由于呼吸器变色存在两种状态，一是自上而下的变色，即呼吸器密封不严导致变色，往往需要重新安装；另一种是自下而上的变色，即正常变色，变色程度达到一定值时需要安装更换。因此该算法分别计算两部分的代表颜色：

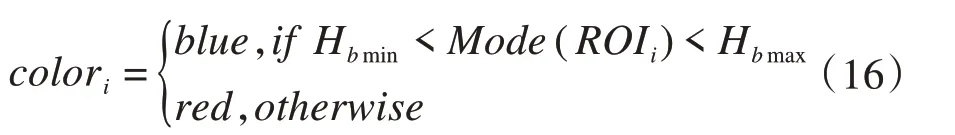
其中：ROIi表示第i个感兴趣区域（RoI，Region of interest），i取0或1；Mode(.)表示取众数的算子；Hbmin、Hbmax分别表示蓝色对应的H通道最低数值和最高数值。

如果判断变色方向是自上而下，需要立刻通知工作人员更换呼吸器；若不是，还需通过ROI0和ROI1的面积判断是否更换呼吸器。根据《Q/GDW 1906-2013输变电一次设备缺陷分类标准》，硅胶潮解变色部分超过总量的2/3时，就可以认为该变压器存在着一般缺陷。因此，当红色硅胶颗粒面积占总硅胶颗粒区域面积达到2/3时需要更换呼吸器。

6 实验结果

图2为待处理原图，使用MSR算法对输入图像处理后的结果如图3所示。可以看出当MSR尺度取0.5、1.0、1.5时最加合适。在此尺度组合下，高光反射区域得到了一定程度上的抑制，同时，硅胶颗粒区域的颜色变得更加鲜艳，边界更加清晰，这有利于我们后续对该区域进行分割。使用同态滤波对输入图像进行处理后结果如图4所示，相较原图颜色鲜艳程度略有提高，但是硅胶颗粒区域产生大量噪声，图像质量变得粗糙，严重影响后续处理。同时由于同态滤波参数较多，不同光照条件下的参数差异较大，因此，MSR算法相较于同态滤波更具有实用性，且适应性更广。

图2 待处理原图

图3 不同尺度MSR效果图

图4 不同参数的同态滤波效果图

将MSR增强后的图像转换至HSV颜色空间，对其H通道执行滤波和二值化，结果如图5所示。经过二值化的H通道已经基本提取出了硅胶颗粒区域，但是还存在一些干扰区域，例如左上角背景，这些位置不属于硅胶颗粒区域，应该予以去除。另外，二值化后的H通道中硅胶颗粒区域的边缘过于锋利，存在许多毛刺，与实际情况不符且不利于后续处理。因此文中采用开运算将这类干扰区域中的较小独立区域消除，并圆滑硅胶颗粒区域的边角，消除毛刺，并使用最大连通域搜索算法排除较大非目标区域。对H通道执行开运算后结果如图6（a）所示，明显较小独立的非目标区域被消除，目标边界也圆滑许多。之后对H通道中剩余被选中区域进行面积统计，以面积为尺度对考察区域进行排序，最大面积对应的区域即为硅胶颗粒区域。结果如图6（b）所示。按照提取出的RoI区域对图5（b）的H通道进行数据提取，结果如图6（c）所示。

图5 H通道处理结果图

图6 H通道RoI提取结果图

将图6（c）的每一列视为一个单独的一维数据，通过对其进行H通道自适应阈值计算，分别得到每一列的分割位置。分割结果如图7中红色点所示。再对分割点集进行拟合，结果如图7中蓝色线所示，分界线符合直观感受和物理规律。按照文中算法红色RoI的面积与总RoI面积的比值为51.4%，而按照传统像素统计的方式计算，红色像素与红蓝色像素之和的比值约为59.6%。经过人工现场比对，该呼吸器变色比例为51%左右，显然所述方法效果更佳。

图7 分割结果图

所述算法应用于不同的呼吸器图像，结果如图8所示。

图8 所述算法分割结果图

7 结语

文中提出一种基于Retinex算法和自适应H通道阈值分割的变压器呼吸器变色自动检测方法，借助于智能巡检机器人现场拍摄并传回的变压器呼吸器装置图像，利用数字图像处理技术对该图像进行分析，并进行决策分析是否需要更换变色硅胶。实现了低成本、高效率、高准确度的识别检测，具有广阔的应用和研究前景。

1）通过使用Retinex算法并调整尺度参数来处理图像，有效增强了原始图像，同时抑制了反射光的干扰。

2）自适应H通道的阈值分割不依赖于先验知识，可以实现自适应的对两区域进行分割，鲁棒性明显优于其他算法，可以适应不同的现场环境。

3）对分割线进行拟合，不仅更加符合人工巡检方式，而且通过划定分界面，抑制了一些由于拍摄角度极端造成图像存在高反射区域的现象对判定结果产生影响。