基于充电数据的多阶段锂离子电池健康状态估计
魏中宝,阮浩凯,何洪文
(北京理工大学 机械与车辆学院,北京 100081)
锂离子电池因为其成本低、能量密度高、可靠性强等优点,成为了电动汽车常用的储能工具. 准确监测电池的健康状态对于电动汽车的安全性和可靠性有重要意义.
电池的健康状态的估计方法通常分为基于模型的方法和基于数据的方法. 基于模型的方法将电池健康状态作为状态变量或模型参数,并使用自适应滤波器对参数进行更新以获得健康状态估计值[1-2].尽管这种方法有较高的估计精度,但对模型精度和扰动的敏感性限制了其在实际场景中的应用[3].
基于数据的方法构建简单的映射关系,根据提取的健康因子推断健康状态[4-5]. 目前,基于数据的方法主要利用标准的恒流恒压充电数据提取健康因子,估计电池的健康状态. 增量容量分析和差分电压分析是该领域最常用的方法. 由于健康因子在电池全寿命周期的一致性,增量容量分析(incremental capacity analysis, ICA)和差分电压分析(differential voltage analysis, DVA)相比得到了更广泛的应用[6]. 基于增量容量曲线的健康因子,即增量容量峰的位置、高度和面积,与电池的老化过程有直接联系[7-8]. 但是这种方法需要繁琐的数据预处理,而且需要一个相对完整的恒流充电数据. 完整恒流充电数据在实车充电中很难得到,因为驾驶员倾向于在锂离子电池电量完全耗尽之前给电动汽车充电. 因此,这激发了学者们对恒压阶段充电数据的研究. 研究表明利用指数函数拟合恒压电流提取时间常数,能有效估计健康状态[9]. 相似的研究还有采用等效电路模型来反映恒压电流的动态变化,并提取健康因子估计健康状态[10]. 此外,研究发现恒压充电电流的变化率和恒压充电时间与电池容量均有很强的相关性[11]. 尽管已有大量研究验证了恒压充电数据的利用价值,但实际工况中,恒压充电阶段通常耗时,获取完整的恒压充电数据同样十分困难.
研究旨在解决上述问题,并提出一种实用的多阶段健康状态估算方法,该方法具有广泛的应用范围,包括应对实际工况中充电数据严重缺失的场景.
1 多阶段健康状态估计算法
1.1 电池数据获取
4 个编号为5、6、7 和18 的标定容量为2Ah 的LiNiCoAlO2(NCA)电池在室温条件下(约25 °C),进行恒流恒压充电和恒流放电循环,如图1 所示. 首先,B5、B6、B7 和B18 以1.5 A 的电流放电,直到端电压分别下降到2.7 V、2.5 V、2.2 V 和2.5 V; 然后,电池以恒流恒压模式充电,其中恒流电流、电压上限和恒压截止电流分别为1.5 A、4.2 V 和50 mA.最后,重复充电和放电循环,直到电池容量衰减30%.
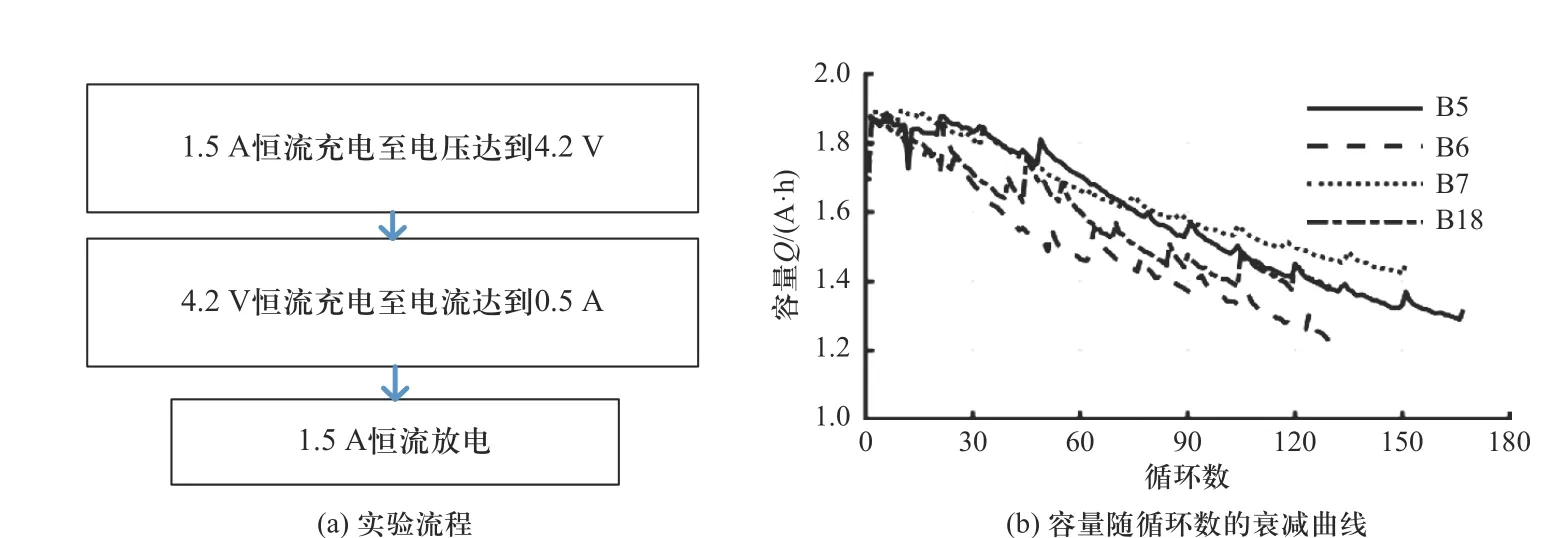
图1 实验流程和电池容量衰退曲线Fig. 1 Experimental procedure and battery capacity degradation curve
1.2 基于完整恒流充电数据的电池健康状态估计
对于可以获得完整恒流充电数据的情景,ICA是目前最普遍的方法. 增量容量曲线是根据恒流充电数据将增量容量与升高的电压相关联而得出的.然而,离散的电压数据通常导致原始增量容量曲线充满了噪声(图2(b)中波动较大的曲线),这极大地阻碍了健康因子的提取. 为了弥补这一缺陷,研究采用高斯函数来拟合曲线,在提取可用健康因子之前消除强噪声. 基于高斯函数,以电池端电压V作为自变量,dQ/dV可表示为

式中:n为曲线中的峰的个数;Ai是第i个峰的面积,A·h;ωi为第i个峰的宽度, V;V0i为第i个峰的几何中心位置, V.通过滤波算法,可以从Q-V曲线上难以识别的电压区域获得易于提取的增量容量峰的参数值. 滤波后的Q-V曲线和增量容量曲线与原始曲线的对比如图2 所示.

图2 原始和滤波后的Q-V 和增量容量曲线Fig. 2 Original and filtered Q-V and IC curves
增量容量曲线随老化的变化规律如图3(b)所示. 从图中可以看出增量容量曲线随电池老化呈现出规律的变化. 由此推断出,公式(1)中的9 个参数均具有作为健康因子的潜力. 为了选取合适的电池健康因子,这些参数与电池容量之间的相关性系数如表1 所示. 从表中可以看出,A1、A2、A3、V2和w3与电池容量的相关性系数较高,因此被选作电池健康状态的健康因子.

表1 参数与电池容量的关系Tab. 1 Relationship between parameter and battery capacity
1.3 基于局部恒流充电数据的电池健康状态估计
从图3(b)中可以看出,当电压超过3.9V 时,增量容量曲线中最明显的峰已经不能完整显示出来.这象征着用增量容量方法估计电池健康状态的效率降低,需要提出新的健康因子弥补增量容量特征的缺失.
之前的研究已经表明,恒流充电时长T与电池健康状态有很强的相关性[12-13]. 但是单独的T并不能实现与增量容量方法相似的估计精度,新的健康因子需要被提出. 如图3(a)所示,随着电池老化,恒流充电过程中的电压增加得更快. 为此,模糊熵(Fuzzy entropy, FE),作为描述时间序列数据混沌程度的有效特征,被提取来描述电压上升速率的变化.FE 的详细算法如表2 所示.

表2 FE 计算流程Tab. 2 Detailed procedures to determine the FE of charging voltage
T和FE分别代表图3(a)横向和纵向维度上的电压曲线的规律性. 结合增量容量曲线第三个峰值的3 个特征,共融合5 个健康因子进行健康状态估计,期望解决初始充电电压超过3.9 V 时恒流充电数据缺失的不利情况.
1.4 基于恒流恒压过渡阶段的电池健康状态估计
当起始充电电压超过4V 以后,图3(b)中可以看出,增量容量曲线的第三个峰也逐渐变得不完整,基于局部恒流充电的方法也开始失效,同时充电电压接近恒流截止电压,意味着充电数据来到了恒流恒压过渡阶段. 在恒流相位向恒压相位转换的过程中,恒流和恒压段数据都处于严重缺失的状态,都没有充足的数据来提取合适的健康因子,如图4 所示. 虽然数据缺失,但是恒流阶段结束时的电压斜率和恒压阶段开始时的电流斜率随循环使用而有规律地变化,这其中必然包含与电池老化相关的信息. 为了充分利用数据的形态学特征,一种常见的处理图像问题的CNN 模型被建立起来,以原始的恒流电压和恒压电流数据直接作为模型输入,估计电池的健康状态.

图4 恒流恒压充电过程中电压和电流曲线Fig. 4 Charging curves during CCCV phase
CNN 是一种强大的深度学习算法,用于图像等多维数据处理. 它由卷积层、池化层和全连接层组成. 由于卷积核参数的共享和层间连接的稀疏性,使得卷积神经网络在计算量较小的情况下捕捉图像的拓扑特征,并且对原始数据没有额外的特征要求. 因此,研究利用CNN 建立输入到电流和电压数据与电池健康状态之间的关系.CNN 使用滤波器或核K执行卷积,该滤波器或核K用于从输入向量a获得特征映射S. 表示为
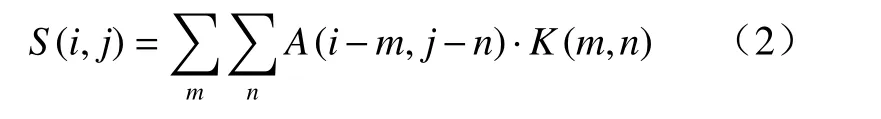
卷积之后,通常添加偏置,并引入非线性激活函数.这里,偏差定义为b,激活函数为h,卷积层输出zi,j为
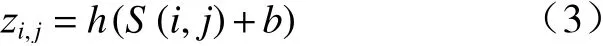
针对恒流恒压过渡段数据,CNN 模型的输入是一个2 行100 列的矩阵,其中包含100 个采样间隔为2.5 s 的电压和电流数据. 权衡模型复杂度和估计精度,CNN 由具有16 个大小为2 的卷积核的一维卷积层、一个具有32 个大小为1 的核的一维卷积层和两个分别具有16 个和1 个神经元的全连接层组成. 由于空间特征与图形输入相比受到限制,因此没有池化层. 此外,卷积核移动步幅为1,并选择ReLU函数作为激活函数. 方法的流程图如图5 所示.

图5 CNN 估计电池健康状态的流程图Fig. 5 SOH estimaiton flowchart based on CNN
2 结果与分析
2.1 基于完整恒流充电数据的电池健康状态估计验证
在第2 章的讨论中,公式(1)中的5 个参数被选作估计电池健康状态的健康因子. 充分权衡电池的非线性特征和算法的复杂度,BP 神经网络被用来建立健康因子与电池健康状态之间的关系. 基于训练电池B5 获得的估计结果如图6(a)所示. 结果表明,健康状态估计值与实验基准值吻合较好,估计误差大多在3%的误差范围内. 尽管电池的化学成分相同,但不同的电池在制造过程中可能会相互偏离. 随着电池老化,电池不一致性也会显著增大. 因此,必须评估所提出方法对电池不一致性的鲁棒性能. 在这方面,使用经过B5 训练的模型来估计电池B6、B7和B18 的健康状态,结果如图6(b)~(d)所示. 在所研究的锂离子电池的整个寿命期间,估算的健康状态与实测的容量衰退轨迹非常相似. 由于电池的不一致性,模型在新电池上的估计精度有一定程度下降,但是,其明显小于5%的误差说明模型的性能是令人满意的.
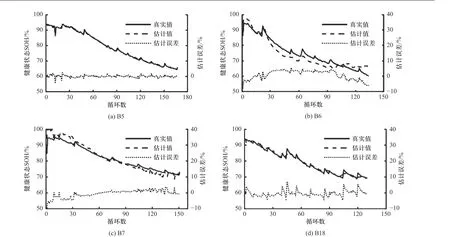
图6 基于完整恒流充电数据的电池健康状态估计:.Fig. 6 SOH estimation based on complete CC charging data
2.2 基于局部恒流充电数据的电池健康状态估计验证
接下来,考察健康状态估计方法在电流数据相对缺失情况下的性能. 此时,充电数据已经损失一部分,初始充电电压在3.9~4 V 范围内,对应的电池的SOC 范围是30%~70%,这是驾驶员由于充电焦虑最可能开始进行充电的SOC 阶段. 提取FE、TRCC、A3、ω3和V03作为健康状态估计的健康因子,考虑到模型的估计精度和计算复杂度,同样使用BP 神经网络来拟合健康因子与电池健康状态的关系. 估算结果如图7 所示.
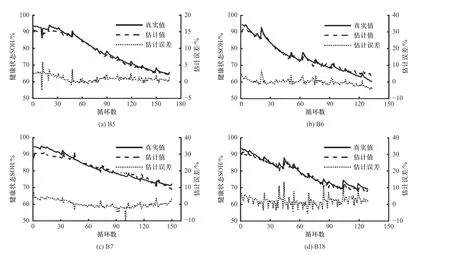
图7 基于局部恒流充电数据的电池健康状态估计Fig. 7 SOH estimation based on partial-CC charging data
从图中不难观察出,即使只有部分充电数据可用,在整个生命周期内,无论是经过训练的电池还是新电池,估计的健康状态仍然与实验标定的真实情况非常一致. 与第3.1 节中的结果相比,可以观察到,估计误差仅略微增大. 即使在初始电压达到4V(对应于[45%,70%]范围内的初始充电SOC)的情况下,也可以精确估计健康状态,MAE 被控制在3%左右.换言之,多阶段、多类别特征融合的健康状态估计方法,使健康状态的估计精度并不会随充电数据减少而明显下降.
2.3 基于恒流恒压过渡段的电池健康状态估计验证
按照图5 中总结的流程,CNN 模型通过电池B5、B6 和B7 进行训练,然后在电池B18 上进行健康状态估计验证. 结果如图8 所示. 结果表明,基于恒流恒压过渡段的充电数据的健康状态估计值与实验基准值吻合较好,估计误差大多在5%的误差范围内.在电池B18 上对训练模型的鲁棒性进行验证,结果如图8(d)所示. 从图中可以看出,CNN 模型可以很好地推广到新电池,即使电池在初始老化状态和循环条件下都不同(如第2.1 节所述). 在缺少充电数据的情况下,证明了该方法对电池不一致性的鲁棒性.

图8 基于恒流恒压过渡段充电数据的电池健康状态估计Fig. 8 SOH estimation based on CCCV transition phase
与第3.1 和3.2 节中的结果相比,估计误差相对增大. 但是考虑到恒流恒压过渡段数据严重缺失的情况,最大不超过5%的健康状态估计误差是满足需求的. 换言之,由于多阶段和多类别特征融合的实施,多阶段的方法能在实际工况中更加有效地估计电池的健康状态.
3 结 论
文中提出了一种多阶段健康状态估计方法,该方法对充电数据严重缺失的情况具有很高的鲁棒性.根据初始充电电压的不同,从有限的充电数据中提取不同组健康因子. 使用神经网络算法对健康因子进行进一步融合,以实时估计电池健康状态. 研究在NCA 电池上进行了长期老化实验,并用实验数据验证方法的可靠性. 主要结论总结如下.
①提取了基于局部恒流充电数据的模糊熵和充电时间作为两个健康因子估计电池的健康状态,弥补了在恒流起始阶段充电数据缺失的场景中增量容量方法的失效. 与使用完整充电数据的情况相比,提出的方法具有相似的高精度.
②提出了基于恒流恒压过渡段数据的电池健康状态估计方法. 利用卷积神经网络从严重缺失的数据中挖掘老化信息. 该方法对实际充电工况有很强的鲁棒性. 即使在初始充电电压达到4.1 V(起始SOC 大于50%)的不利情况下,健康状态估计的最大误差也不超过5%.
③结合了增量容量方法提出了一种具有实际应用价值的多阶段健康状态估计方法. 该方法对电池不一致性具有很强的鲁棒性,在训练和测试的锂离子电池上都有很高的估计精度.

