流速及丙烷体积分数对丙烷-水两相混输的影响研究

韩 霄，张洪涛，张 林，张 锋，吕良广

（青岛市特种设备检验研究院，山东 青岛 266100）

自20 世纪70 年代以来，随着众多油气田被发现和开采，越来越多的油气输送过程开始采用多相流混输技术。相比于油气资源单独输送，多相流混输技术能够节约大量的人力物力，同时也更容易实现自动化控制，具有显著的经济潜力[1]。相比于单相输送，多相混输过程中流动介质的多样性往往存在复杂的流动状态，不同流体可能存在速度差异，进而形成不同的流型，影响介质的输送。目前，工业生产中常见的多相流混输包括气液、气固、固液两相流以及气液固多相流等等，其中气液两相流被广泛应用于油气混输、油气润滑等领域[2-4]。由于管道运输具有成本低、稳定性高等特点，气液两相混输多采用管道进行运输。而在气液两相混输过程中，稀相（气泡或液滴）会对管壁产生空蚀以及冲刷腐蚀的影响，严重影响管道的长期使用[5]。有研究表明，气泡的存在会对气液两相流管道产生冲刷腐蚀，最终引起管道穿孔[6]。而在弯头处，管道的曲率发生突变，更容易受到流体冲刷作用。随着陆上以及海上油气田开采工作向深处发展，油井产物会存在大量如二氧化碳、硫化氢等腐蚀性介质。这些腐蚀性介质会对管道形成严重的化学腐蚀，影响管道使用寿命。而混输过程中稀相对管壁的冲刷作用会加剧管道的腐蚀程度。此外，油气混输过程中油气比的不同也会对流体介质的输送产生一定影响。随着混输两相体积分数的改变，管道中的流型发生改变，严重时形成段塞流，阻塞介质的输送[1，3]。

随着计算流体力学（CFD）的发展，越来越多的学者采用数值模拟的方法对气液两相流中的流动及冲刷腐蚀问题进行研究。王祺来[7]对空管投油过程中的V形起伏管道进行气液两相流模拟，发现在V 形起伏管道的下倾管段存在滞止气囊即形成段塞流。聚集的气相以气囊的形式滞止于下倾管段，使得液相流通面积减小，导致液相流速突然增大；气液两相在管道内存在相互作用，滞止气囊体积的改变会引起局部压力波动，进而影响流动稳定性，造成局部水力参数不稳；在整个管道中，滞止气囊以段塞形式移动，会引起整个管线水力参数不稳。随后王祺来研究了不同参数对滞止气囊的影响，并提出安全合理的运行方案，给出了相应的排气措施。张欣雨等[8]通过Fluent 软件模拟研究了V 形起伏管道中的气液两相流动，对不同管径、入口流速以及管道倾角下气泡的生成以及运动行为进行研究，最终得到了空管投油过程的临界流速。该研究得到的临界流速公式对于实际起伏管道投产过程中投油速度的选取具有一定指导意义。管孝瑞等[9]通过数值模拟方法研究了集气站埋地集气管道以及地面以上集气管道内的冲刷腐蚀问题，指出了集气管道中存在的液相沉积现象以及容易受到冲刷腐蚀的管道部位。结果表明，集气管道不同位置处存在不同程度的液相沉积，特别在弯头处液相沉积更为显著，液相在管道底部的沉积增加了管道的腐蚀风险。吕运容[10]研究了石化行业中高温条件下环烷酸的流动腐蚀行为，并给出了工程防护方法。此外，有学者对微通道内的气液两相流问题展开了研究[11]。

近年来π形输送管道在热力输送过程中得到广泛使用，其复杂的管道结构使得其内部流动特性并不同于普通弯管，为了研究π形管内部的流动规律，一些学者开展了对π形管的多相流动研究，主要包括对于π形管（π形补偿器）的结构优化设计[12-13]、受力特性分析[14]以及π形管在液固、气固两相流动中的冲蚀磨损研究[15-18]。本文基于气液两相流理论，对实际工程应用中某水平放置的π形丙烷-水两相混输管道进行模拟研究。通过观察π形管内流场结构并改变入口流速以及丙烷体积分数来研究其对于丙烷-水两相混输的影响，本研究对于了解π形管内部的流动特性，掌握π形管内部流动规律以及气液两相混输过程的流动规律具有一定指导意义。

1 数学模型

1.1 多相流模型

本文采用欧拉（Eulerian）多相流模型对管道中的丙烷-水两相流动进行模拟研究[19-20]。该模型能够精确模拟气液两相流问题，其任一相的连续性方程为：

式（3）中：μq和λq分别为q相的剪切粘度和体积粘度。

1.2 湍流模型

湍流模型采用基于RANS 方法的Realizablek-ε湍流模型[21]。该模型对分离流和具有复杂二次流特征的流场具有较高的求解精度。Realizable k-ε模型的湍动能k以及湍流耗散率ε方程如下：

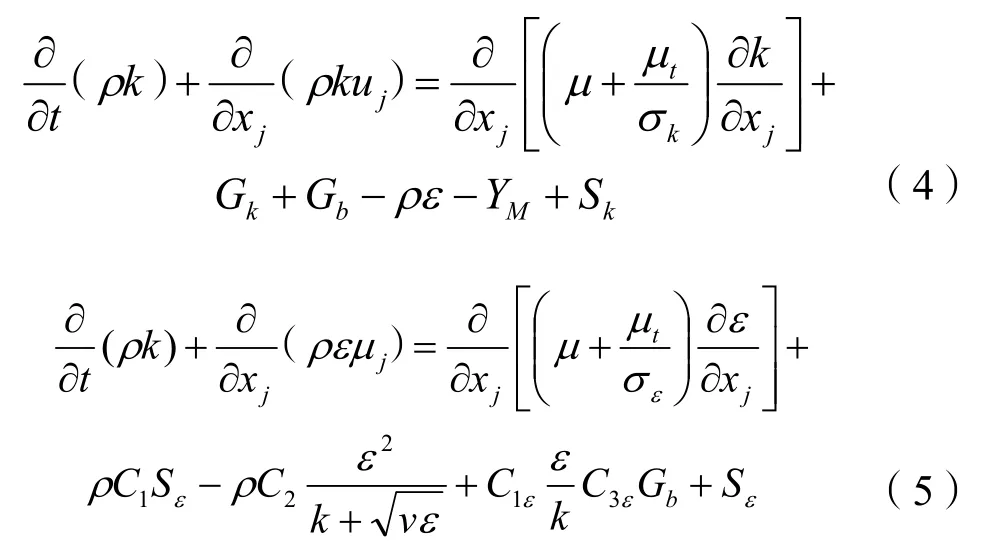
式（4）（5）中：σk、σε分别为k、ε的湍流普朗特数，其值分别为1.0 和1.2；Gk和Gb分别为由平均速度梯度和浮力产生的湍动能；YM为可压缩湍流中脉动膨胀对整体耗散率的影响；Sk和Sε为源项；C1=max[0.43，C、C为模型默认常21ε数，其值分别为1.9、1.44。

1.3 模拟参数

本文对不同流速以及丙烷体积分数条件下水平放置π形管内丙烷-水两相混输流动进行模拟研究，丙烷-水物性参数如表1 所示，模拟所需操作变量如表2 所示。 在模拟时边界条件分别选择速度入口（velocity-inlet）以及压力出口（pressure-outlet），压力-速度耦合方法采用SⅠMPLE 耦合方法，压力离散格式采用PRESTO 离散格式，其余均采用QUⅠCK 格式，壁面采用固定无滑移边界条件。

表1 丙烷及水物性参数

表2 操作参数

2 几何模型

2.1 几何建模与网格划分

本研究所采用几何模型为水平放置π形管道，管道几何模型及尺寸如图1 所示。其中，π形管管径D=500 mm，弯头曲率半径r=1.5D，弯头两侧直管长L=6 m。为得到高质量的结构化网格，采用ⅠCEM 软件对网格进行O-block 划分，并对边界层部分网格进行局部加密。弯头以及管道横截面处的网格如图2 所示。

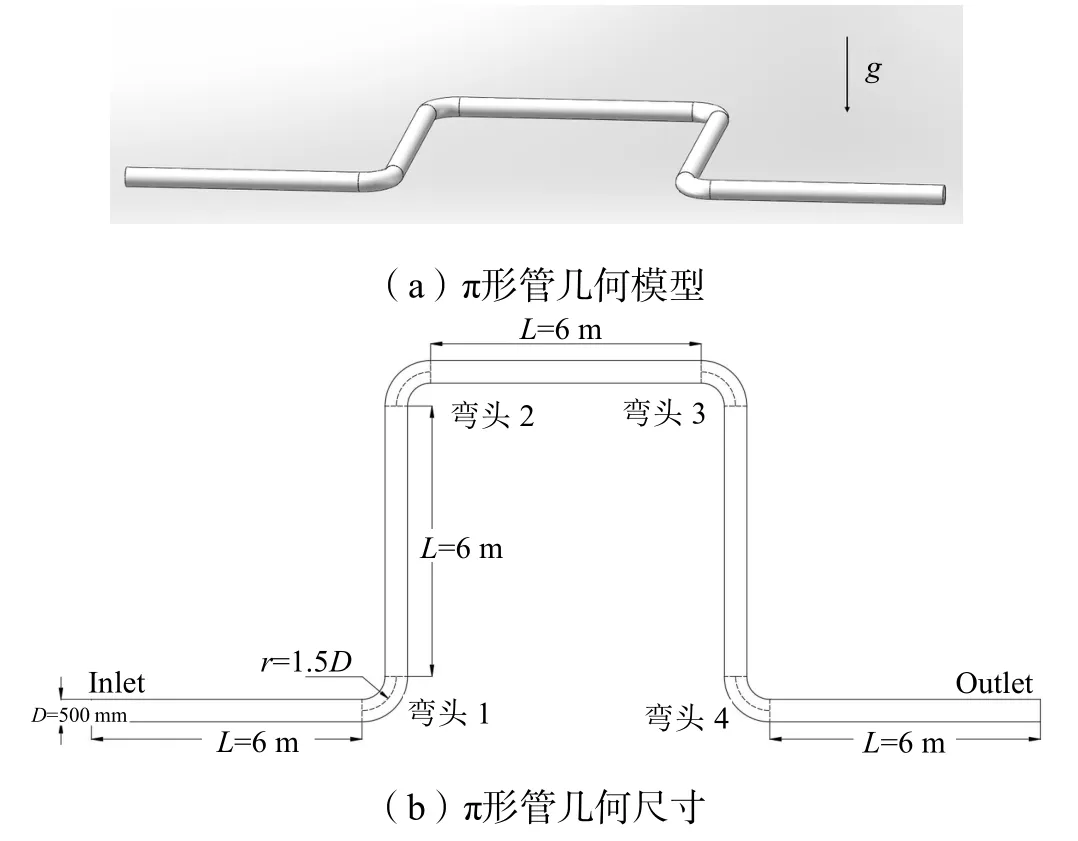
图1 π形管几何模型及尺寸

图2 π形管网格划分

2.2 网格无关性验证

为同时考虑计算精度以及计算效率，对模拟所需网格数量进行无关性验证。不同网格数量下管壁的最大剪切力变化如图3 所示。由图3 可知，随着网格数量的增加，壁面最大剪切应力逐渐增加，当网格数量达到797 122 以后，壁面最大剪切应力基本达到稳定，因此采用网格数为797 122 的网格开展后续模拟研究。

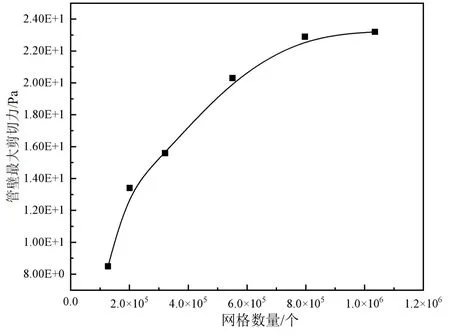
图3 网格无关性验证

3 结果与讨论

3.1 流场分布

流速2.5 m/s、丙烷体积分数为5%时π形管管壁的压力分布如图4 所示。由图4 可知，管壁压力沿π形管轴向位置的改变而变化，同时由于π形管水平放置，在重力方向上存在明显的压力梯度。在π形管入口直管段，气液两相沿管道轴向流动，压力轴向分布基本不变。而当气液两相流经弯头时，由于管道曲率发生突变，气液两相受到离心力作用，使得弯头处压力分布发生变化。在管道内部，靠近弯头内拱的流体受到的离心力较小，速度大，产生的动能较大，因此这部分流体的比压能小，压力较低；相反，靠近弯头外拱的流体所受离心力较大，速度小于内侧流体，比压能较大，压力较高。因此，在4 个弯头处，压力分布均表现为弯头外拱压力高于内拱压力。同时在流动过程中，由于重力作用，液相始终位于管道底部，气相聚集在管道顶部，使得在不同轴向位置处管道底部的压力显著高于管道顶部，造成了4 个弯头处非对称的压力分布。

图4 管壁压力分布

该条件下管道中心截面水相的速度分布如图5 所示。由图5 可知，π形管的速度分布在直管部分比较均匀，而在弯头处则存在一定差异。在π形管第一个弯头前的流动区域，液相速度基本保持均匀分布；而在弯头处，由于管道曲率突变，流体受到离心力作用，导致弯头内侧流体流速高于外侧流体，形成如图5 所示的速度梯度，这与图4 中弯头处的压力分布相符；此外可以看到，由于弯头曲率引起的流向变化，流体在流入下游直管时无法迅速充满整个管道，在弯头内侧与下游直管的连接处存在一定范围的低速区，随着流体的继续流动，管道内的速度分布最终趋于均匀。

图5 中心截面液相速度分布

不同流速以及丙烷体积分数下π形管管壁最大压力的变化规律如图6 所示。由图6 可知，随着流体中丙烷体积分数的增加，π形管管壁最大压力线性降低；随着入口流速的增大，管壁压力显著增加。从图4 压力分布云图可知，π形管管壁最大压力位于管道底部的液相区。当流体中丙烷体积分数增加时，其分压作用更加明显，使得液相（水）所占分压减小，因此π形管管壁最大压力线性降低。当管道入口流速增加时，流体自身动能增大，对管壁的冲击作用增大，最终导致管壁压力增加。

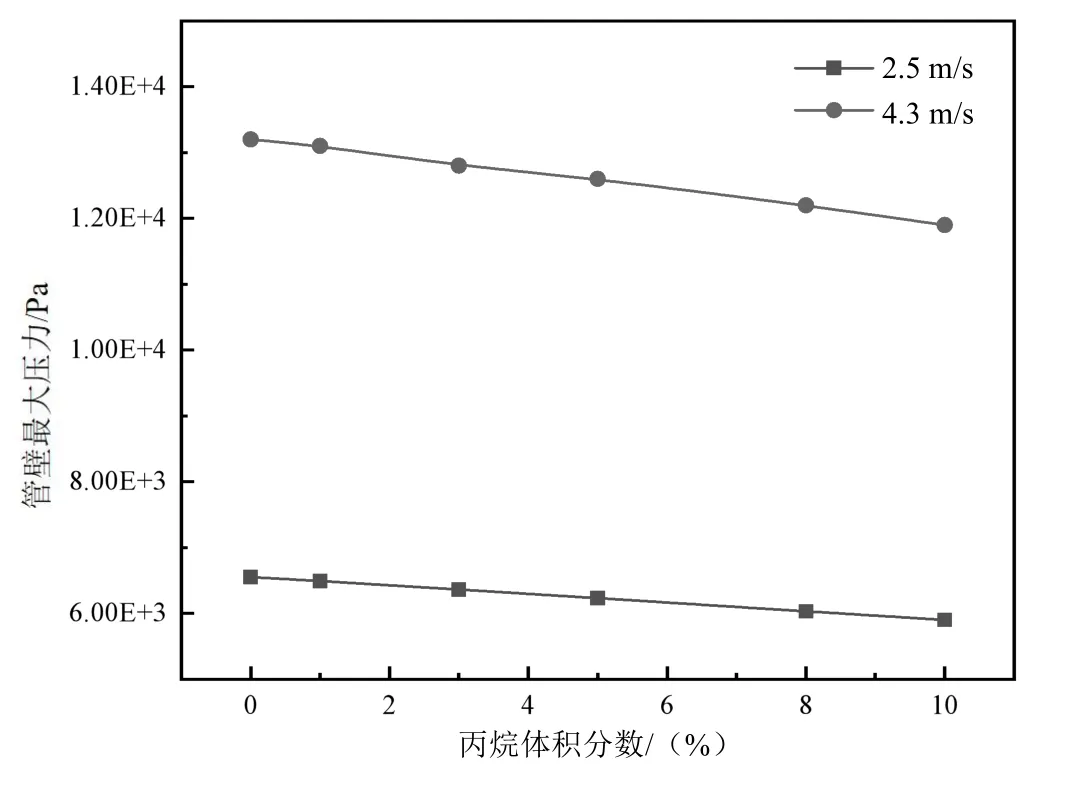
图6 不同流速以及丙烷体积分数下管壁最大压力变化

3.2 丙烷分布

丙烷体积分数为5%时不同流速下π形管壁面的丙烷分布云图如图7 所示。由图7 可知，丙烷在π形管的不同位置分布不同。在π形管入口处，丙烷和水两相分散较为均匀，而随着流体的流动，丙烷主要集中在管道顶部；在各弯头处，丙烷所受离心力较小，因此主要聚集在弯头内侧；当气液两相流出弯头时，丙烷在管道内呈现出均匀分布，随着在下游直管中的流动，丙烷再次聚集到管道顶部。由于π形管内流体流向与重力方向垂直，丙烷需要克服重力跟随液相流动。在流动过程中，由于气液两相密度差较大，水相对于丙烷的携带能力较差，丙烷有向上运动的趋势，在流动一定时间后上升到管道顶部并发生聚集。丙烷聚集在管道顶部形成连续的气相区，使得最终得到的丙烷体积分数减少，不利于丙烷的管道运输。同时，气相聚集使得π形管横截面上的有效流通面积发生急剧变化（当气相聚集严重时形成段塞流），极易引起管道局部位置压力波动甚至π形管整体压力变化，增加管道输送的水头损失，不利于管道长周期运行。此外，对比图7（a）及图7（b）可以发现，随着入口流速的增加，丙烷聚集区域的面积有所减小，且管道顶部丙烷的体积分数下降。这是由于当流速增加时，丙烷自身动能显著增大，对于液相（水）的跟随性增强，丙烷能够更好地沿着主流方向流动，其在重力方向上的二次流动减弱，因此在管道顶部的聚集程度降低，聚集区域面积减小。

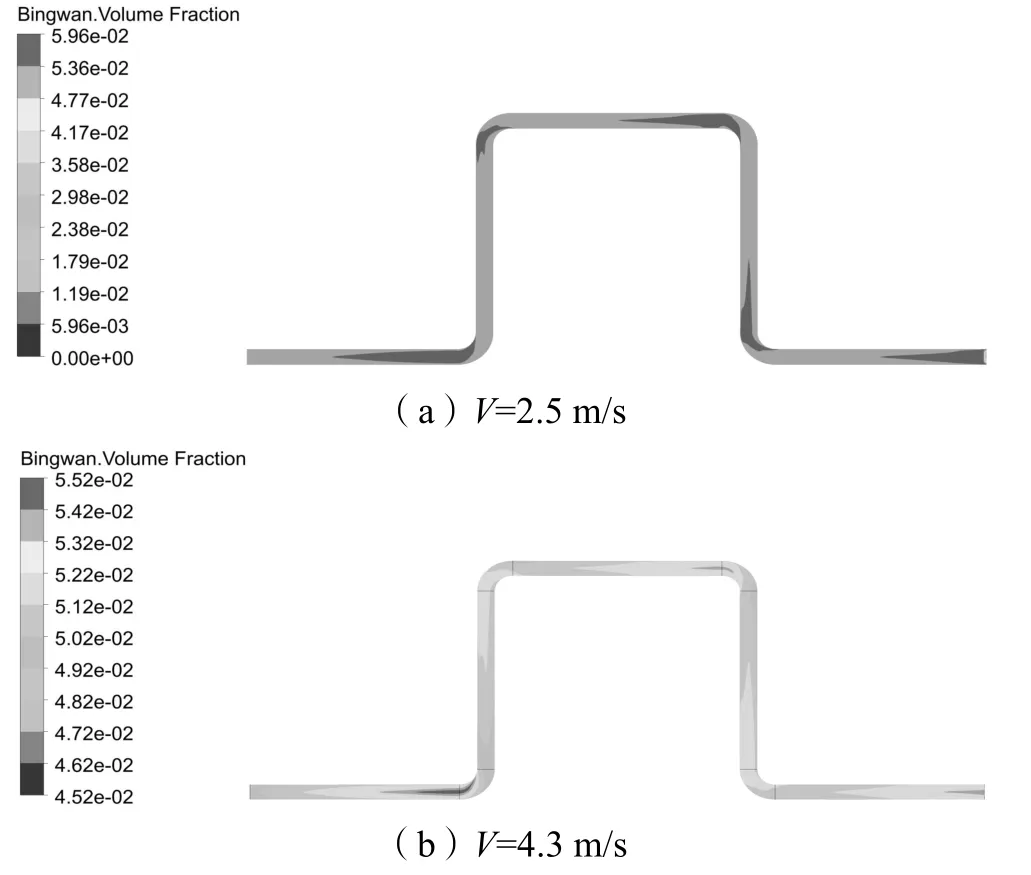
图7 不同流速下π形管管壁丙烷分布

不同流速以及入口丙烷体积分数下管壁丙烷最大体积分数的变化规律如图8 所示。由图8 可知，随着入口丙烷体积分数的增加，管壁丙烷体积分数呈现出线性增大的趋势；随着流速的增大，管壁丙烷体积分数出现小幅度下降，且入口丙烷体积分数越大，管壁丙烷体积分数下降越明显。当管道入口丙烷体积分数增加时，管道内的整体丙烷体积分数增加，在流动过程中更多的丙烷受重力影响聚集到管道顶部，使得管壁丙烷体积分数增加；而随着流速的增大，管道内丙烷动能增大，对液相的流动跟随性增强，对重力的抵抗效果更显著，最终导致丙烷在管道顶部的聚集程度减弱。研究结果表明，管道流速的增加使得丙烷在管道内的流动性增强，减小了丙烷在管道顶部的聚集，有效减轻了管道内的压力波动，有利于丙烷的长期运输。

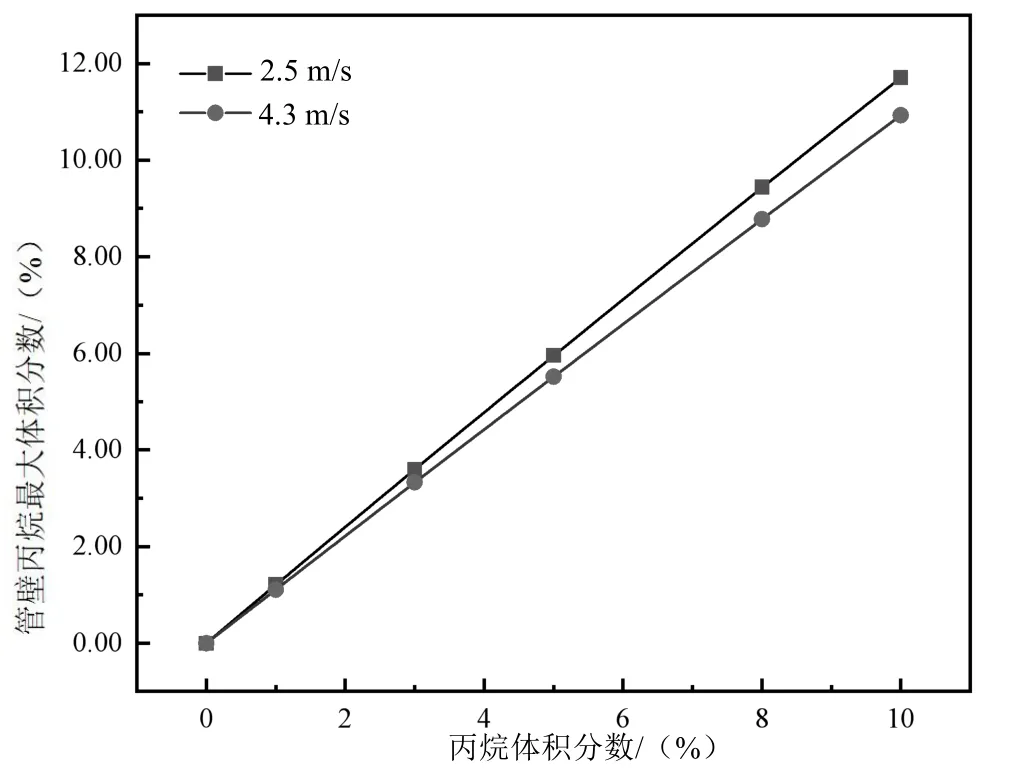
图8 不同流速以及入口丙烷体积分数下π形管管壁最大丙烷体积分数变化

3.3 剪切力分布

管壁剪切力表示了流体对于管壁的剪切作用，管壁剪切力越大，流体对于管壁的剪切和冲刷作用越大[9]。不同流速下丙烷体积分数为5%时π形管管壁的水相剪切应力分布如图9 所示。由图9 可知，π形管管壁受到了不同程度的液相剪切作用。在各直管段，管壁剪切力分布均匀且变化较小；而在弯头处，管壁剪切力则有明显不同。由于弯头处管道曲率的变化，流体被迫改变流动方向，对管壁产生剪切作用。同时，由于弯头内侧流体流速较大，对弯头内拱的剪切作用明显高于外拱，极易导致壁面厚度减薄，甚至穿孔。此外，在弯头与下游直管的连接处也出现了一定范围的高剪切力区域。这是由于靠近弯头内拱的流体在流过弯头时沿内拱切线方向运动，使得弯头与下游直管连接处出现高剪切应力区域；同时，由于弯头引起的管道曲率变化，流体在流过弯头后在短时间内无法迅速充满整个管道，因此连接处的剪切应力径向分布并不均匀。

图9 不同流速下π形管壁面剪切力分布

不同流速以及入口丙烷体积分数下管壁最大剪切力的变化规律如图10 所示。由图10 可知，随着入口丙烷体积分数的增加，管壁最大剪切力线性下降；随着流速的增大，管壁剪切应力显著增大。当管道入口丙烷体积分数增加时，管道内的丙烷体积分数增大，液相体积分数减小。当单个水分子对管壁的剪切作用不变时，由于水的体积分数的减小，液相整体对于管壁的剪切作用减小，使得管壁剪切力减小。而随着流速的增加，液相自身动能增大，在流动过程中对于管壁的冲刷和剪切作用增强，最终导致剪切力的增大。模拟结果表明，流速的增加会使得管壁剪切力增加，不利于管道的长期使用，因此在实际运输过程中，要合理选择流速大小。

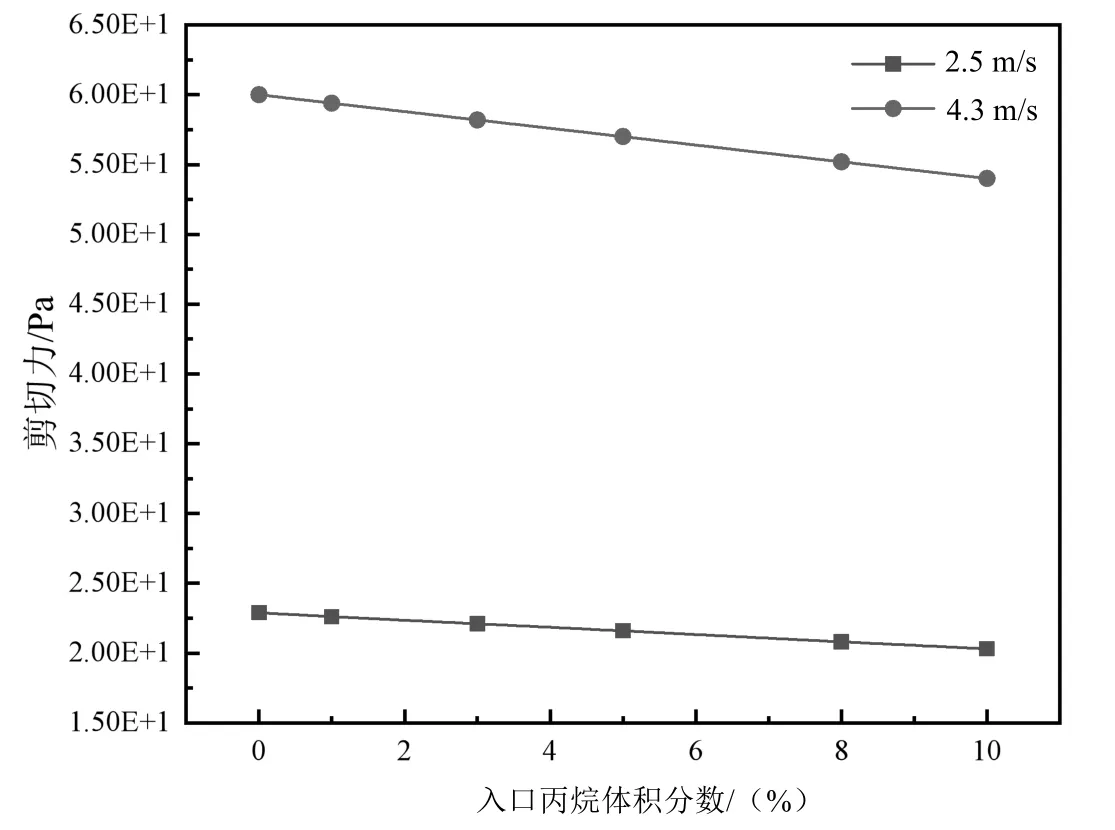
图10 不同流速以及入口丙烷体积分数下π形管管壁最大剪切力变化

4 结论

本文通过欧拉（Eulerian）多相流模型以及Realizablek-ε湍流模型对水平放置π形管进行丙烷-水两相混输流动模拟研究。对不同入口流速以及丙烷含率下π形管内流场分布、管壁丙烷分布以及剪切力分布进行具体研究，得到的主要结论如下。

在水平放置的π形管内，液相对于丙烷的携带能力较差。由于流体主流方向与重力方向垂直，在流动过程中丙烷需要在重力作用下跟随液相流动，逐渐在管道顶部形成丙烷聚集区，不利于丙烷的输送。

随着入口流速的增加，气液两相动能显著增大，管路流动更稳定。由于流速的增大，管壁丙烷的最大体积分数有所降低，丙烷在管道顶部的聚集程度减弱，有利于丙烷的输送；而液相速度的增大会导致管壁受到的液相剪切作用增强，引起管壁压力增大，不利于管道的长期使用。

随着入口丙烷体积分数的增加，管道内丙烷的体积分数增加，造成管道顶部丙烷聚集程度的增加，不利于丙烷的运输；由于丙烷体积分数增加，管道内液相的体积分数减小，引起水相分压减小，对于管壁的剪切作用减弱，最终导致管壁压力降低。

在实际运输过程中，为保证丙烷管道输送的稳定性，应控制管道入口丙烷含率以及流速在合理范围内，减小丙烷在管道顶部的聚集，减轻对输送介质以及管道的损害。