一种面向多测量系统的数据融合方法

刘倩頔，赵子越，乔 磊，孙安斌，曹铁泽，贾志婷

（中国航空工业集团公司北京长城计量测试技术研究所，北京 100095）

随着智能制造的发展，以航空航天为代表的大型装备制造业不断进行技术革新，因此在其部件制造和装配的过程中将面临复杂的测量需求，这种情况下采用一种测量设备往往难以满足需要，需要多种或多站位的测量设备共同完成测量任务，因此，出现了多测量系统的数据融合问题[1]。

测量系统的数据融合是指构建一个基准坐标系，将多个测量系统的坐标系统一到基准坐标系，从而达到多测量系统能够在统一的基准下协同工作的目标，同时需要保证测量精度[2]。目前，解决这类问题的方法一般是利用公共点进行坐标系转换，现有的公共点坐标系转换方法较为成熟的包括奇异值分解法和四元数法[3]。这2 种方法均需要对公共点的三维空间坐标进行融合，完成坐标系转换，如果在点位精度不够的情况下，其转换精度会受到较大的影响。因此，解决这类问题需要完成以下2 方面的工作：建立相对稳定的公共点，作为空间坐标的承载体；研究一种高精度的数据融合方法，提高协同测量的精度[4-6]。

针对以上问题，本文首先设计了一种基准转换标准器，上面固定多个基准点的靶标，能够保证相对位置的稳定性，然后研究了一种基于多传感单元的数据融合方法，最后通过实验证明了装置和方法的有效性和精度。本文中的多测量系统可以指不同的测量系统，也可以指同一个测量系统通过移动不同的站位，通过这种模式完成一个测量任务。

1 数学模型

多测量系统数据融合的目标是在满足精度指标的前提下，将不同系统的测量数据统一到同一个坐标系下，可描述为n个测量站位或系统通过m个公共点完成数据统一，其测量模型可以表示为：h（O，C）=0，如图1 所示。图1 中，模型的输入量C由第i台仪器或站位对第j个公共点的测量值cij和其不确定度uij组成，其中i=1，2，3，…，n，j=1，2，3，…，m。测量值cij根据传感单元的不同，一般可分为长度、角度等几何量参数，以激光跟踪仪为例，它的观测量为距离、水平角和垂直角，可以通过观测量转换为三维坐标。输出量由n-1 台系统或站位的位姿参数（仪器坐标系到全局坐标系）Oi=（αi，βi，γi，txi，tyi，tzi）组成，有了这些数值，m个公共点的坐标pj=（xj，yj，zj）T在全局坐标系下的数值即可计算出来，从而完成了多测量系统的数据融合。

图1 数据融合方法的数学模型

2 基准转换标准器设计

2.1 基准转换标准器的结构

基准转换标准器主要由碳纤维基准组件和姿态调整架组件组成（如图2 所示）。其中碳纤维基准组件由碳纤维板材组成，具有结构稳定和受温度等参数影响小的特点，上面安装7 个基准靶标，能够完成不同系统的坐标转换。姿态调整架组件由铟钢制作完成，起固定和支撑作用，可以直接安装在三脚架上，同时可以旋转90°，保证在不同角度中使用。基准转换标准器在不同角度下的使用示意图如图3 所示。

图2 基准转换标准器的组成

图3 基准转换标准器配合三脚架在不同角度下的使用效果图

2.2 基准转换标准器的精确赋值

基准转换标准器需要对其中的靶标进行准确赋值，一般这一环节采用3 坐标测量机测量7 个靶座（P1—P7）的位置和立方镜（C1、C2）的位置和角度。其中P1—P7代表靶座上放置标准球后的球心位置，C1、C2代表标准立方镜的中心坐标。立方镜及销孔位置示意图如图4 所示。

图4 立方镜及销孔位置示意图

基准转换坐标系的定义规则是以P1为坐标系原点，以P1、P2、P7这3 个中心点构成的平面朝外的法向方向作为Z轴的正方向，以P1和P7的连线（朝向P7）的方向作为X轴的正方向，右手定则确定Y轴。具体步骤如下：使用半径1.5 mm 的触发测头，在每个靶座上放置一个标准球，利用25点法在标准球上取点，利用25 点拟合球面，从而求得球心的坐标；测量3 个构建靶座基准坐标系的靶标球心位置，构建靶座基准坐标系；建立好靶座基准坐标系后，依次测量剩余的靶座；使用直径1.0 mm 的触发测头，对选定的立方镜的各个面进行测量，每个面上取16 个点，根据该16个点拟合平面，确定立方镜各个面在基准坐标系下的法矢量，构造立方镜面1 与面3 的中分面、面2 与面4的中分面，用2 个中分面与面5 联合求取三面交点，将该交点在中分面交线方向进行偏移量修正，得到修正后的交点，该交点为立方镜中心点；最终输出一组在靶座基准坐标系下的点位坐标。点位坐标值在试验环节的数据表格中给出。

3 基于多传感单元的数据融合方法

目前采用多个公共点完成数据融合的方法依赖于测量系统的点位精度，而点位精度主要依赖于传感单元，从这个角度来讲，从传感单元的角度完成数据融合和优化更为直接，而且利用传感单元构建约束方程更利于加权处理。现有的测量系统从传感单元的范畴可分为角度和距离约束2 类，例如激光跟踪仪属于角度加距离约束，摄影测量、经纬仪、室内GPS 等系统属于角度交汇约束，激光跟踪干涉仪属于距离交汇约束。数据融合示意图如图5 所示，室内GPS、数字相机、激光跟踪仪等系统均测量同一个基准点，不同的系统按照传感单元进行数据融合，室内GPS 和相机是水平角和垂直角2 个角度约束，激光跟踪仪是水平角、垂直角和距离3 个约束[7]。因此，需要在数学模型的基础上构建角度和距离的2 类约束方程。

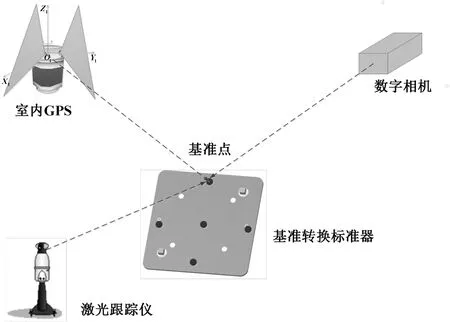
图5 多测量系统数据融合示意图

本文中，约束方程用hij表示，它代表了仪器传感单元观测量、基准公共点坐标及仪器位姿参数的数学表达关系，可表示为：

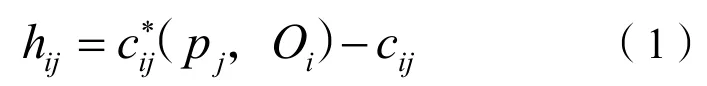
按照以上规则，距离观测量可列写约束方程如下：

角度参量约束方程可列写如下：

考虑到约束方程最终求解的参量为长度量，因此需要将上述方程改变为长度量，方程可改写如下：

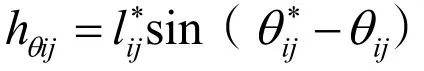
以上结合不同传感单元的观测量列写长度量纲下的约束方程，从而构建约束方程组，如何求解约束方程组是急需解决的任务，目前这一求解问题是一个多目标优化问题，利用评价函数转换为单目标优化是一个可行的解决方案。本文利用最小二乘的原理[8-9]，利用加权平方和法构建评价函数如下所示：

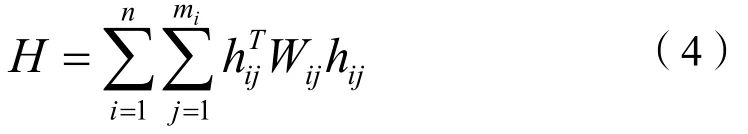
式（4）中：Wij为表示约束方程的权值的权矩阵，这就能保证每个站位下的传感单元的观测值与约束方程对应，方便直接加权，权值确定的准则是按照传感单元观测量的不确定度确定的。

在优化过程中，观测量不确定度小的约束方程应该给予更高权值，约束方程hij的权值Wij可以表示为：

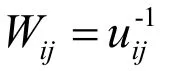
说明观测值的不确定度uij越小，约束方程hij的约束越强，对应的权值Wij越大，因此达到加权最小二乘的效果。求解这一评价函数需要完成非线性优化求解，得到方程的解即为待求的位姿转换关系，从而完成数据融合的过程。

4 实验验证

为验证本文研究的基准转换标准器和数据融合方法的可行性和正确性，在实验室环境下设计了以下试验，利用激光跟踪仪在多个站位下对基准转换标准器进行测量，通过本文的方法完成优化，实验环境如图6所示。

图6 试验验证环境

采用激光跟踪仪多个站位完成基准转换标准器的数据采集，利用本文中的数据融合方法建立约束方程，利用评价函数完成优化求解，为评价方法的精度，利用解算出来的姿态参数计算对应的基准点坐标，利用基准点的坐标值偏差来衡量方法的精度，数据表格如表1 所示。

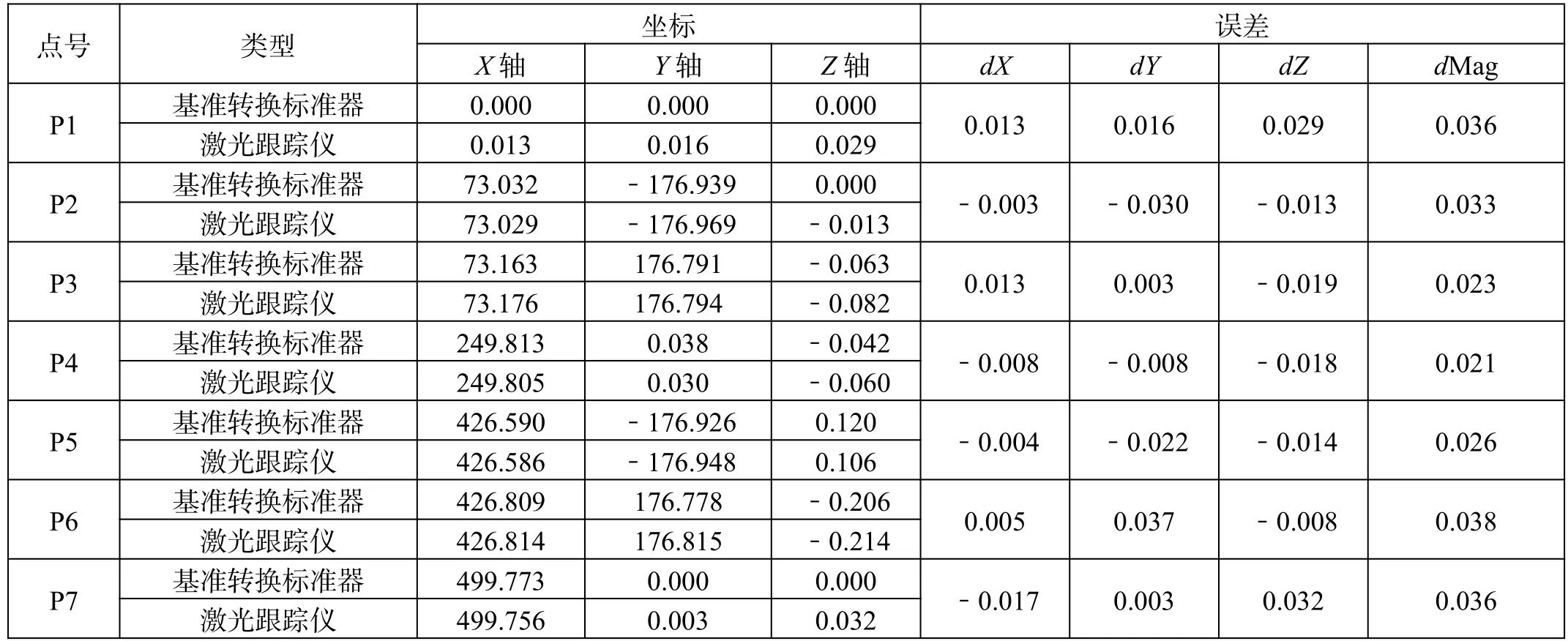
表1 精度对比试验数据（单位：mm）

表1 中是7 个基准点的数据，对比了基准转换标准器和激光跟踪仪的数据，转换误差中dX、dY、dZ分别代表X、Y、Z这3 个坐标轴方向的误差，dMag代表坐标点在空间中的转换误差，即：

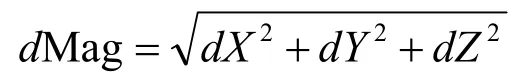
试验数据表明，7 个基准点的转换误差均在0.04 mm 以内，另外，通过多次重复性试验也达到满足现场工程使用的要求，也证明了方法的正确性。

5 结论

本文针对大型装备制造过程中的多测量系统的协同测量问题，规划了一种数据融合方法，设计了基准转换标准器作为数据融合的承载硬件，同时研究了一种基于多传感单元的数据融合方法，阐述了约束方程的构建方法，设计评价函数并按照加权方法完成了最小二乘求解。最后，利用激光跟踪仪进行了精度验证试验，基准转换误差优于0.04 mm，满足工程应用要求。