三相油浸式变压器开路热源分析

王 欣 蔡现龙 王效洪

（1．陕西 西安 710061；2．西安明德理工学院，陕西 西安 710061）

0 引言

三相油浸式变压器是在电磁、流体和温度等多种因素的作用下运行的，当运行环境不稳定以及设备发生故障时，会加剧变压器的损耗，导致过热、提高阻抗、降低绝缘强度甚至损坏设备，因此需要对油浸式变压器进行空载试验，以发现设备的设计及加工缺陷，验证各项技术标准和工况，及时根据变压器的热源分布情况快速了解设备的运行状态，并根据变压器各关键部件的使用环境和温度推算其使用寿命，确保变压器可以安全、稳定地运行[1]。

基于有限元法的热源分析数值模型对变压器铁芯进行合理化网格处理，能很好地对变压器的热源分布情况进行数值分析。设定必要的边界条件，建立适当的仿真模型，利用COMSOL软件可以较真实地对变压器的热源分布情况进行仿真，为研究人员提供一种直观的认识，并根据实测的一手数据和仿真结果帮助研究人员解决技术难题。

1 三相油浸式变压器的铁芯空载损耗分析

变压器的空载损失包括铁芯损失和因无负载电流引起的线圈欧姆损失，因为线圈损失比铁芯损失小得多，所以其可以忽略。而在构成铁芯损失的因素中，影响最大的是磁滞损耗、涡流损耗和磁场波形崎变损耗。其中，主要的影响是磁滞损耗和涡流损耗，在工程计算中往往不考虑磁场波形崎变引起的损耗。超过99% 的空载损失来源于铁芯，尤其是铁轭与铁芯柱相接处的损耗最大。

1.1 涡流损耗

涡流损耗可划分为纵向损耗和横向损耗。

横向涡流损耗如公式（1）所示。

纵向涡流损耗如公式（2）所示。

在单元体积中的涡流损失如公式（3）所示。

变压器总的绕组内的涡流损耗如公式（4）所示。

式中：Bri、Bzi分别为第i个栅格的横向磁感强度（T）和纵向磁感强度（T）；ρ为线圈的电阻率，Ω·mm2/m；b为导线的纵向长度，mm；d为导线的横向长度，mm；Ri为第i个栅格的重心到芯部的中心线的间距，mm；Si为第i个栅格内导体的面积，mm2。

1.2 磁滞损耗

在铁芯重复被磁化的过程中，由于滞后效应所产生的能量被称作“滞后损失”，因此该损失的大小与磁滞回线的面积呈比例关系，如公式（5）所示。

式中：C2为硅钢板（与材料性能相关）的材料系数，m；Bm为最大磁通量；ρ为表示硅钢板的电阻率；f为磁场反转频率，Hz；t为叠片厚度，m。

2 三相油浸式变压器流体场和热源分布的基本理论

2.1 温度场

物体的结构不同、厚度、位置以及导热条件不同，产生或测量的温度就不相同。通常，试验中会得出以下结论 ： 物体在空间位置上的每个点都只有一个唯一的温度值。将该物体所有点的温度值进行综合就构成了温度场。

温度场可用空间坐标和时间的函数来描述，如公式（6）所示。

2.2 流体场与温度场的耦合计算

三相油浸式变压器在空载运行时有自己特定的温度场，主要分为流体场和固体场。铁芯、绕组和绝缘材料为固态域，空气、变压器油为流体域[1]。

铁芯、绕组是油浸式变压器固体域的主要组成部分，其产生的损耗会使变压器的温度升高，产生的热量将在固体结构上经过热传导的方式传递到固体结构的外表面和变压器油中，属于纯导热。这就涉及流体——固体耦合边界的传热问题，如公式（7）所示。

式中：QC为热传导的热量，W；λ为导热系数，W/（m·K）；x为进行热传导的距离，m；S为构件接触面积，m2；T1、T2为物体表面温度，℃。

当接触面、导热系数和温差呈增长态势时，单位时间内传导的热量会越多[2]。

根据三相油浸式变压器铁芯的传热过程建立数学模型，结合变压器流体场和温度场的特点，分别建立三维导热控制方程和三维对流控制方程。三维导热控制方程如公式（8）所示。

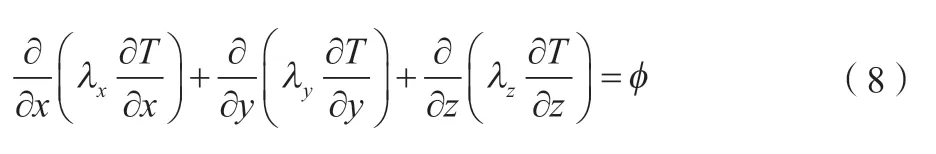
式中：λx、λy、λz分别为x、y 、z方向的导热系数。Ø为内部热源密度。

三维对流控制方程：

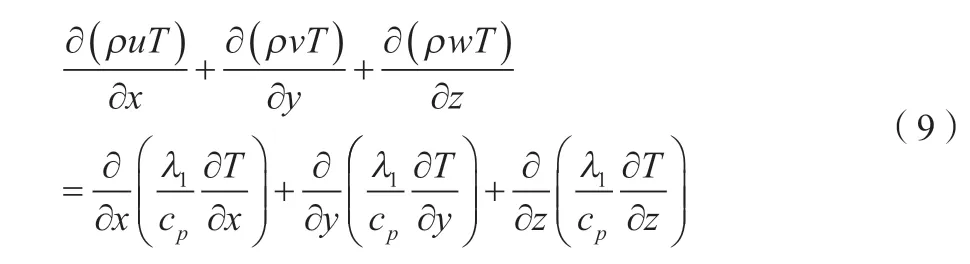
式中：u、v以及w分别为x、y以及z方向的速度分量；ρ为流体（变压器油）密度；Cp为变压器油比热容；T为温度；λ1为流体（变压器油）的导热系数，J/(cm·s·℃)。

由热流密度连续性的条件可以得到关于流体域和固体域的导热系数公式，如公式（10）所示。

式中：n12、n21分别为分界面的热流从流体流向固体、固体流向流体；λ1为流体域的导热系数，W/（m·K）；λ2为固体域的导热系数，W/（m·K）。

综合分析可以得到三相油浸式变压器流体场和温度场的控制，如公式（11）～公式（15）所示[2]。

式中：ρ为变压器油的密度，kg/m3；μ为变压器油的动力黏度，Ns/m2；u，v为速度矢量U在X，Y轴上的速度分量，m/s；k1，k2为油浸式变压器油和设备内固体域的导热系数，W/（m·K）；T为温度，K；Cp为变压器油的比热容，J/kg·K；qA为变压器固体域的热流密度，W/m3。

公 式（11）、公式（13）以及公式（14）表示油浸式变压器流体域的质量方程和动量方程，用于求解速度场。公式（15）表示变压器流体域的能量方程，公式（12）为变压器固体域的热传导方程。

根据边界设定条件并结合具体试验分析可知，在公式（12）中，因为固体本来没有速度，速度为0 m/s与表示项相同，所以该项满足要求。公式（15）和公式（12）的导热系数分别为k1/Cp和k2，因为2个公式的计算结果均是常数，所以在模拟时只需要在不同的位置输入相应的值即可；公式（15）的热源为0 m，而公式（12）的热源为铁芯上的热流密度，因为其为常数，所以在模拟时也只需要在不同的网格内赋予相应的值即可。

通过公式（11）能够得出油浸式电力变压器流体场u、v的具体数值，因此可以得出油浸式电力变压器的温度T，从而可以研究变压器内的流体场分布情况[1]。

3 三相油浸式变压器热源分布的有限元分析及仿真对照

有限元数值计算的基本原则为变分原理和加权余量法，为了提高计算速度和网格精度，将铁芯划分成有限个独立的单元网格。根据不同的计算精度，应用插值基函数构建待求解量的近似解，然后利用每个积分方程对求解域进行积分处理，运用加权余量法和变分原理将已知的偏微分方程转换为离散形式的代数方程，最后归总为集合有限元方程。

3.1 建立三相油浸式变压器仿真模型

3.1.1 模型简化

基于计算量、节省计算机空间以及节省计算时间等因素，将模型简化如下：1）将变压器铁轭、铁心柱等简化为阶梯型。2）忽略变压器内部金属结构的影响。3）将变压器结构部件的材料视为均匀且各向同性的材料[3]。

3.1.2 变压器参数设定

额定容量为400 kVA，高压侧额定电压为15 kV，低压侧额定电压为400 V ，高压绕组内半径为18.300 cm，高压绕组宽度为3.102 cm，低压绕组内半径为14.500 cm，低压绕组宽度为2.800 cm，绕组高度为19.200 cm，变50压器铁芯硅钢片个数为8个，变压器铁芯硅钢片递缩量为3.000 cm

在COMSOL软件环境下，根据以上模型简化和参数设定，三相油浸式变压器的三维仿真模型如图1所示。

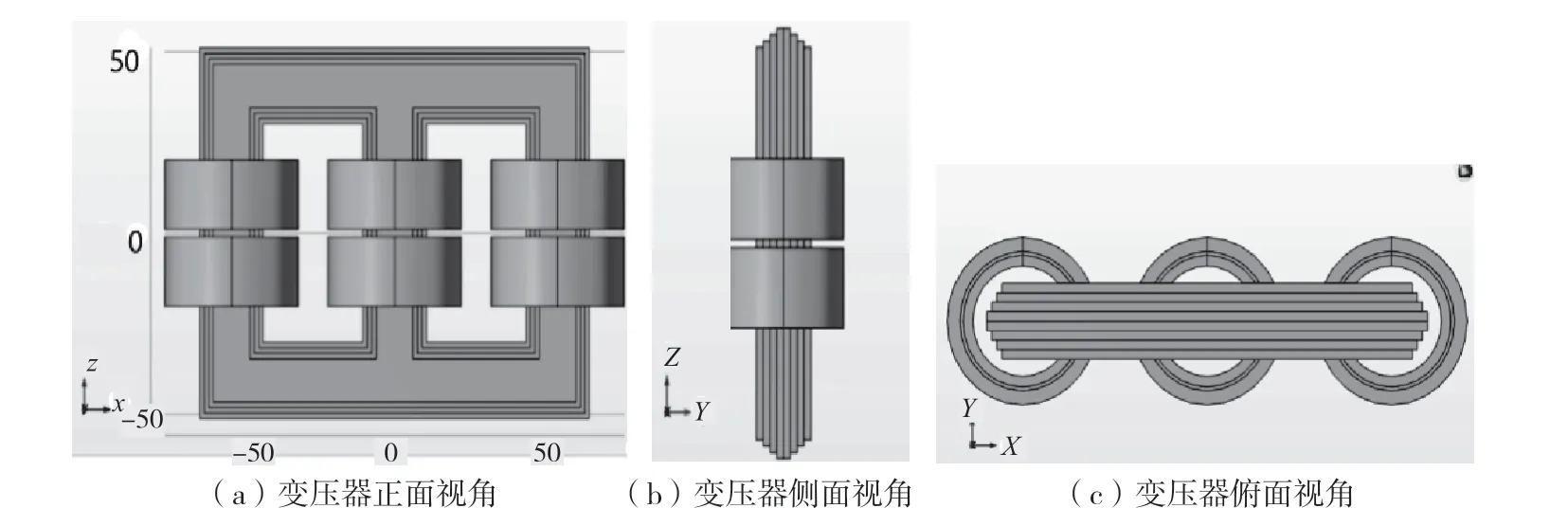
图1 油浸式变压器三维模型

3.2 油浸式变压器网格划分

当采用有限元方法进行数值分析和模拟时，为了避免网格分割的质量影响数值模拟的准确性，不增加计算量并缩短计算时间，采用以下分割策略：铁芯采用四面体的分割方式，绕组采用棱柱的分割方式，网格顶点一共有28 058 个，以四面体为单元的共有146 586 个，以棱柱为单元的共有5 520 个，以三角形为单元共有29 906 个，以四边形为单元共有3 600 个，边界单元和顶点单元分别有7 014 个和380个。在模型域中的单元数为153 606 个，最小的单元质量为0.160 5，其平均单元质量为0.645 9[4]。

已经分割完毕的网格图样如图2所示， 图2（a）～图2（d）是在不同观察角度下对铁芯进行网格分割的示图。

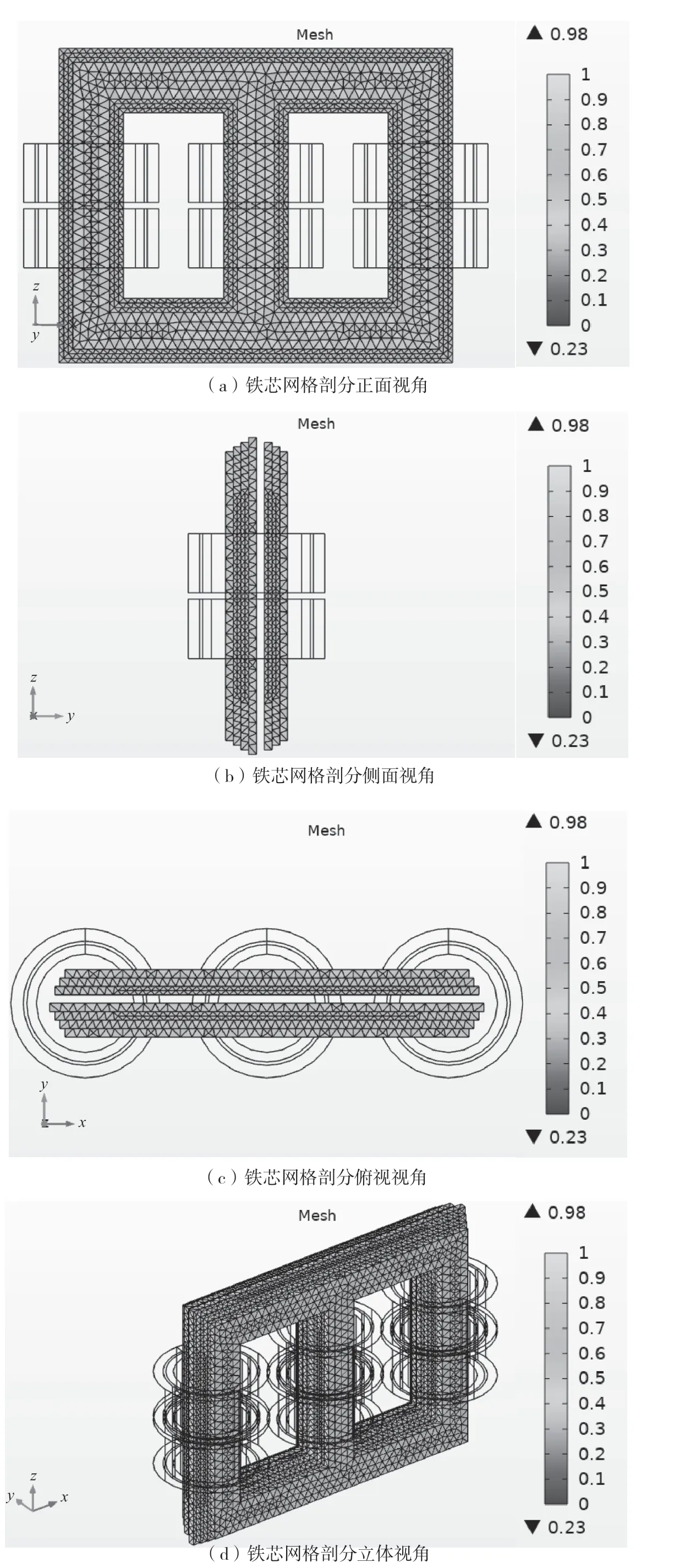
图2 三相油浸式变压器COMSOL铁芯网格剖分图

3.3 三相油浸式变压器的热源分布及COMSOL仿真对照

COMSOL仿真系统中三相油浸式变压器的总热源分布情况如图3所示，变压器内部铁芯温度差别较大[2]。在三相铁芯柱上，热源除在铁芯柱与铁轭的交界处有明显升高变化外，当铁芯柱上的热源热源小于0.02 W/mm3时，发热源最低功率在719×10-6W/mm3。在铁轭的四角处，因电流引起的磁场成封闭椭球状，因此发热量为最小，小于7.19×10-6W/mm3，在铁轭与铁芯柱相接处存在涡流场，因此铁芯产生相应的损耗，其发热量达到相对最高点，为0.02 W/mm3～0.08 W/mm3，且以相接处为中心向四周呈热量降低的发散态势。在三相铁芯柱上除与铁轭相接部位和铁轭中间的部分外，其他区域热量大致相同，密度范围小于0.02W/mm3。

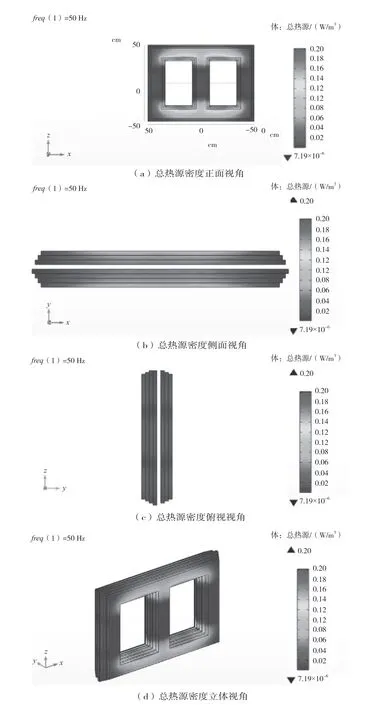
图3 三相油浸式变压器COMSOL开路总热源密度示图

铁芯的热点位置与变压器的热点相同，热源并不在铁芯的顶端，而是在铁芯的上半部。

4 结语

仿真结果表明，三相油浸式变压器在空载运行状态下的热源功率主要位于铁轭的中间部位，铁芯柱中间部位的热源功率次之，与理论分析一致。

综上所述，可以给出以下建议：为降低三相油浸式变压器的空载损耗，可以通过改变铁芯的片宽的方式来降低铁芯的单位铁损，并可以通过改进硅钢片接缝工艺的加工方法（例如焊接）来降低空载时因铁芯硅钢片接缝过大而导致的磁阻。