砂土中吸力筒沉贯阻力模型试验研究

任彦忠 赵学亮 李扬扬 隋淑环 宋启明 游先辉

(1.华北电力大学，北京 102208；2.中广核(福建)风力发电有限公司，福建 福州 350001；3.东南大学混凝土及预应力混凝土结构教育重点实验室，江苏 南京 211189；4.福建永福电力设计股份有限公司，福建 福州 350001)

1 研究背景

风能发电是世界上发展最快的可再生能源利用技术，海上风电场的建设以其优越的风能资源、日趋成熟的发电技术逐渐成为可再生清洁能源技术领域研究和开发的焦点。目前常用的海上风电机组基础型式有单桩式、重力式、多桩式等。吸力式筒型基础是近年来从深海基础中逐渐发展起来的一种新型的海上风机基础。相比传统海风风机基础，它具有施工安装方便、方便拆除等优点，可替代复杂的嵌岩施工技术。

针对吸力式筒型基础安装阻力问题，国内外的学者们对此进行了系列相关研究。Allersma等[1]进行了砂土和黏土地基上的吸力式基础离心机试验，发现在砂土中吸力锚安装方便，而且将沉箱土移出后测量发现箱内壁摩擦力起更多作用。Tran等[2-4]利用物理模型试验和数值模拟的方法，探究吸力桩负压沉放过程的土体孔压变化规律，发现在临界负压状态时沉放过程与孔压发展关系密切。Gao等[5]在砂土地基上进行基础安装沉放和抗拔物理模型试验，进一步分析了桩基础安装和抗拔特点。

理论计算与数值模拟方面，Houlsby和Byrne[6-7]通过简化计算模型，建立了黏土和砂土条件中沉放阻力的公式，此分析过程中简化处理比较多，需要使用详细的地质分析资料，因此对地质勘察提出更多挑战。Andersen等[8-9]通过分析黏性土和砂土地基中带裙基础、不同平台不同荷载形式的锚，创新性地提出了沉贯阻力和承载力的计算方法。根据Andersen等的观点，可以使用静力触探的方法计算砂土中裙板基础贯入阻力。Dyson等[10]在钙质砂土中使用离心机开展物理模型试验，根据试验结果，最终可以得到在不同安装方法和不同加载速率条件下的修正因子。王胤等[11]在砂土中研究负压沉贯过程中土塞的特征与机理，着重分析砂土渗透性，并将锚内砂土渗透系数的变化规律引入到 Houlsby 和 Byrne 理论模型中，对已有的吸力锚沉贯吸力理论模型进行了改进。

对吸力筒的安装阻力，不同学者提出了不同的方法，本文对砂土中吸力筒沉贯安装阻力进行了模型试验研究，用于验证对比不同计算方法的准确性。

2 试验过程

参考已有研究结果可知，砂土中吸力筒沉贯阻力大小主要受内外侧摩阻力大小影响，筒的直径和沉贯深度是侧摩阻力的重要影响因素，因此本试验主要考虑不同直径筒在沉贯过程中阻力的特性，筒长径比的范围由目前国内外研究结果与实际工程经验确定，模型试验参数及方案设计如表1所示，试验中所使用砂土的物理参数如表2所示。

表1 模型试验单桩尺寸

表2 试验用砂物理参数

试验过程包括自重下沉阶段和负压下沉阶段，具体包括:第一阶段，基础在自重作用下沉入土中一定深度，1-R135,2-R170,3-R210自重下沉深度分别为10mm,19mm,14mm，最终达到稳定；第二阶段，使用真空调节罐与真空泵逐级施加荷载，先使用真空泵抽吸负压调节罐内部空气，使得负压调节罐内部达到预定的真空度，然后关闭真空泵，打开调节罐与试验模型的连接阀路。待模型在稳定负压的作用下下沉稳定后，关闭管路调节阀门，负压逐渐消散。在负压作用下基础继续下沉，当吸气管中由气体变为纯净的水流，说明由于负压的存在，筒内水面上升，而继续下沉后，吸气管内出现明显的砂子，说明筒顶已与土塞接触，沉贯最终完成，吸力筒的安装过程见图1。

(a)自重下沉 (b)负压沉贯下沉中期 (c)抽气管出现水流 (d)抽气管出现砂土

三组模型试验在负压沉贯结束后均产生了土塞，1-R135试验工况土塞高度为86.2mm,2-R170试验工况土塞高度为69.5mm,3-R210试验工况土塞高度为69.1mm。可以发现，直径越大的筒，土塞高度越低。实验中土塞高度偏大，可能和加载方式有关。

3 试验结果分析

3.1 负压沉贯过程

将分级加载得到的三组负压—沉贯深度曲线进行比较(见图2),三个筒模型除了直径不同，其余参数均相同，三个筒沉贯曲线差别较小，不过仍能发现相同负压条件下，R=210mm的筒沉贯深度最，R=135mm的筒沉贯深度最小，沉贯所需负压随直径的增大而有一定的减小趋势。

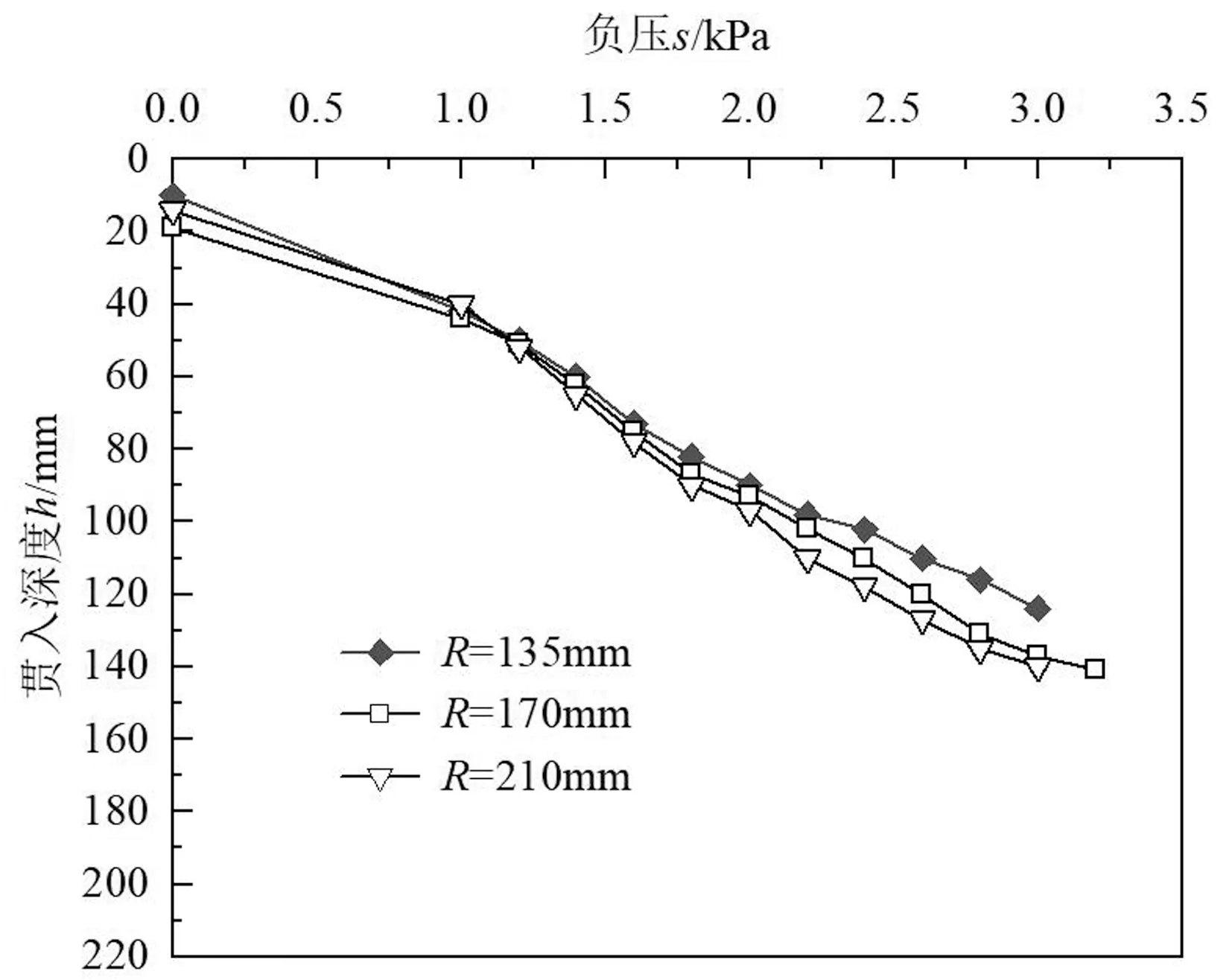
图2 负压—沉贯深度曲线

3.2 试验结果与理论方法比较

计算砂土中沉贯阻力大小，比较常用的方法有Houlsby and Byrne理论方法、DNV规范推荐的基于CPT的方法，以及Senders和Randolph推荐的方法等。其中Houlsby & Byrne[7]推荐的计算方法如式(1)：

(1)

式中，V′代表桩自重；s代表安装所需吸力；D代表桩径(下标o和i分别表示桩外与桩内对应参数)；h代表吸力桩安装深度；α代表粘结系数；t代表筒壁厚度；Zi为代表性参数，体现应力增强的范围和土性。

该计算方法中所需参数如地基承载力系数Nq，Nγ在实际工程较难获得，与砂土内摩擦角有关，本文中取值为30和52；地基承载力系数K在通过室内试验结果和原位测试结果反推得到的值范围在0.8～1.85，因此本实验中选取K值等于1.1;吸力锚与砂土之间的摩擦角δ可参考Andersen的确认方法，选取摩擦角δ= 0.9φ。

DNV规范推荐基于CPT试验所获得的锥体阻力qc的计算方法如下：

R=Fi+Fo+Qtip

(2)

其中：

(3)

(4)

Qtip=Atipkpqc(L)

(5)

根据以往的工程经验，锥体阻力qc随深度变化qc=0.02+2616z。

DNV规范中，kf的建议范围为0.001(最可能值)～0.003(预期的最高值)；对于kp是0.3(最可能值)～0.6(预期的最高值)，本文中，kf=0.002，kp=0.5。

DNV推荐方法未考虑渗流效应，Senders和Randolph[12]基于此提出了一种改进的计算方法，即:

(6)

其中scrit为临界负压，Senders和Randolph[12]利用有限元数值模型，建议临界负压计算方法如下:

(7)

为验证这几种计算方法的实用性和准确性，现将本文试验中施加负压与按Houlsby & Byrne理论解法、DNV推荐方法、Senders和Randolph理论解法计算沉放所需负压进行比较。几种方法的计算结果如图3所示。

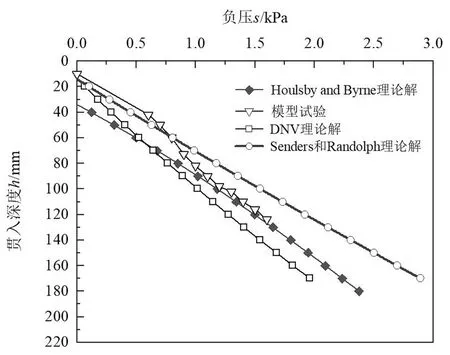
(a)R=135mm

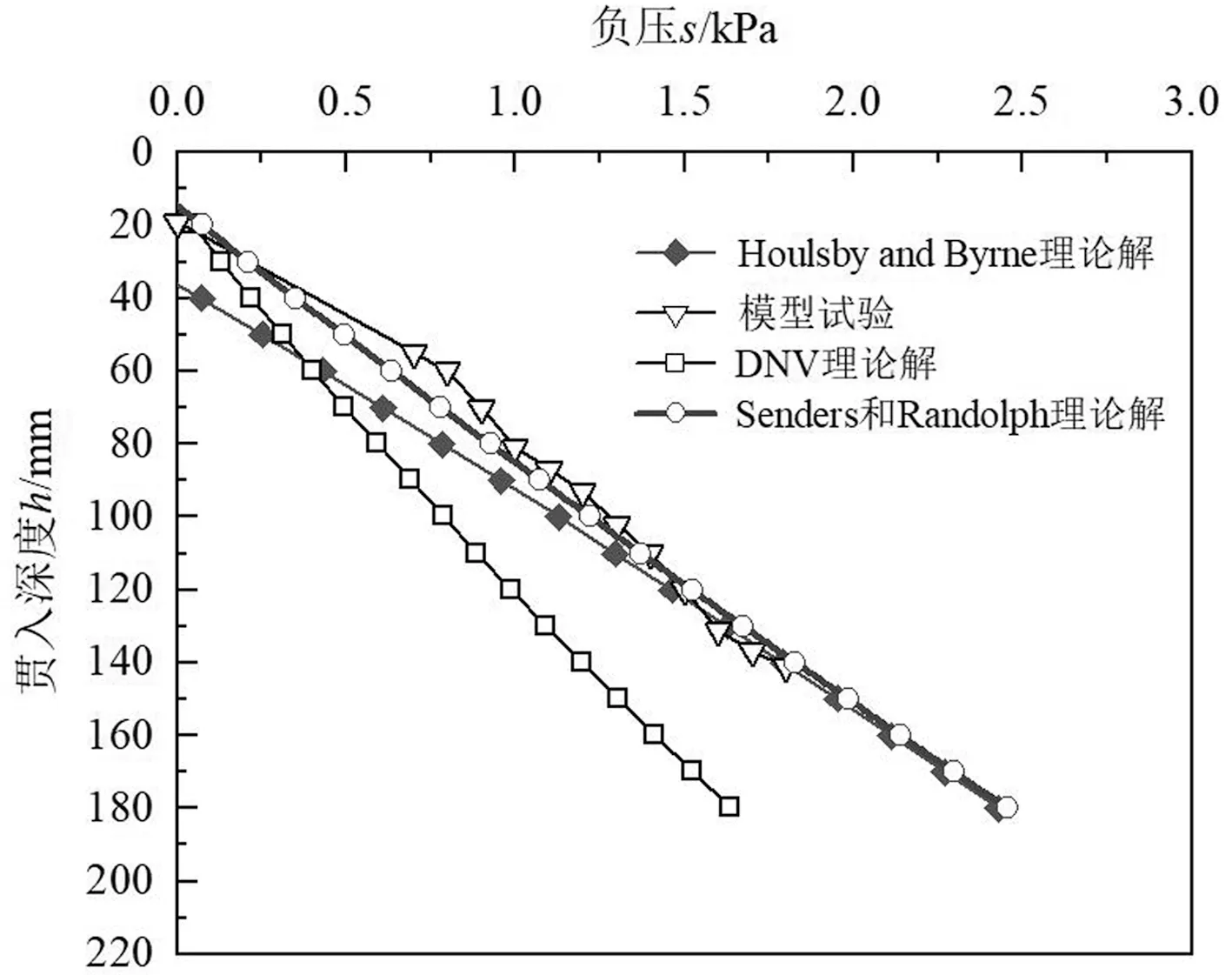
(b)R=170mm

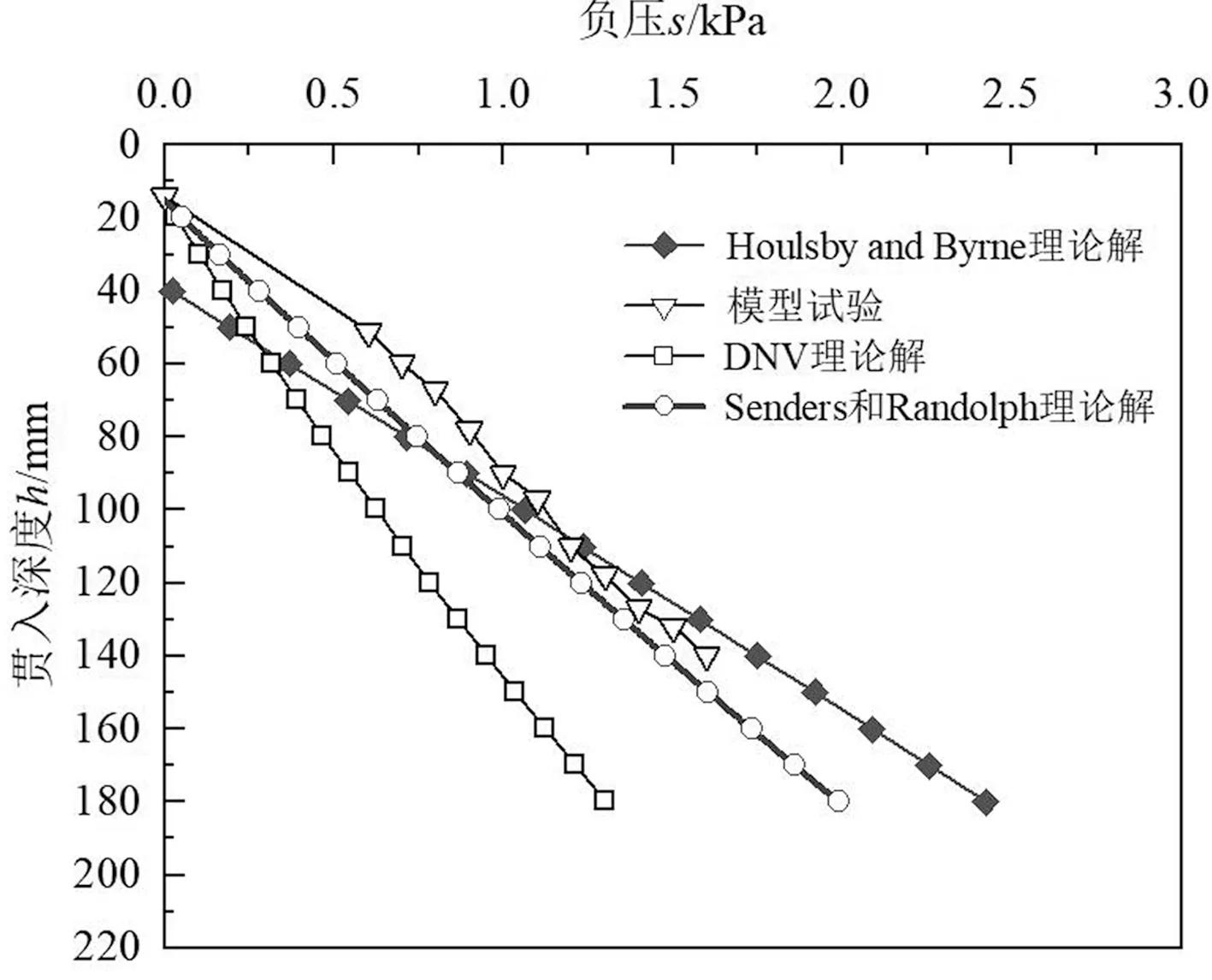
(c)R=210mm图3 沉贯所需负压对比

由图3可以看出，在三组工况下，模型试验结果均与Houlsby & Byrne法有较好的契合度，虽然负压较小时理论计算得到所需负压小于试验结果，偏于保守，主要原因可能是Houlsby & Byrne的理论计算中，假设中筒内为理想渗流状态，而模型试验中由于尺寸效应等原因，导致在小负压时，筒内渗流未充分发展。但当负压增大至1.3kPa时，两者趋向近似。

DNV法求得结果在相同沉贯深度时，所受到的沉贯阻力最小，其原因可能是挤土效应使得筒周围土体应力水平提高，强度参数增大。由于筒壁的约束作用，内侧土体的挤压程度远大于外部土体，而且筒壁内外侧的侧壁摩擦力也不同，基于CPT试验的方法计算时没有考虑内外侧土压力的不同，造成沉放阻力计算值较测量值偏小。同时，由于筒体内部土体的强烈挤压和土塞效应，筒端土体也不可避免地受到挤压，因此，DNV法筒端下沉阻力计算值可能偏小。

Senders和Randolph法相较于DNV法更接近于实际试验结果，体现了其相较于DNV法考虑了渗流带来的优异性，但其和DNV法均受筒径影响较大，随着筒径增大，贯入同一深度所需负压减小明显，在实际运用时需考虑适用的筒径范围。

4 结论

通过吸力筒沉贯模型试验，得到吸力筒负压—沉贯深度曲线，并将结果与Houlsby & Byrne、DNV、Senders和Randolph推荐的方法所求得的理论解进行对比，发现Houlsby & Byrne方法最为接近试验结果，不足之处在于小负压情况下偏于保守，而随着负压增大至1.3kPa时，理论计算结果与试验结果相近。而规范DNV推荐的方法求得的沉贯阻力偏小，Senders和Randolph法对其有改进，但受直径影响波动较大。