基于混沌和线性反馈移位寄存器的彩色图像加密算法

秦秋霞，梁仲月，徐 毅

(大连民族大学 a.计算机科学与工程学院；b.理学院、预科教育学院，辽宁 大连 116650)

当今时代科学技术发展日益更新，信息数据的安全性引起了人们的广泛关注[1-3]。其中，彩色图像由于色彩丰富，形象生动的特点被人们广泛使用。本文提出了一种基于混沌和线性反馈移位寄存器的彩色图像加密算法，可以实现安全、高效的加密，保护彩色图像的安全。

混沌系统通常指的是一种非线性的且具有复杂动力学行为的系统[4-5]。其中经典的低维混沌系统，因其简单、易实现的特性，被反复使用在加密算法中。李等人[6]提出了一种基于Arnold变换和混合混沌的图像加密算法，通过改进Arnold混沌映射，增加迭代规则的多样性，使得置乱效果更好。班等人[7]为了解决加密算法计算复杂度高的问题，提出了一种基于一维混沌映射的高效图像加密算法，加密效率得到了大幅的提高。何等人[8]提出了一种基于二维混沌映射的AES加密算法，将二维混沌映射应用到AES加密算法中，提高了算法的安全性。朱等人[9]对于一维混沌系统的图像加密算法进行了研究和分析，并且提出了一种基于Logistic混沌映射加密算法，低维混沌参与加密使得密钥管理更加方便，加快了加密速度。张等人[10]提出了基于一维混沌映射和比特块置乱的图像加密算法，通过使用经典的Logistic混沌映射对图像进行第一次置乱，然后对分块后的图像进行二次置乱，双重置乱保证了更好的置乱效果。从上述可知，在低维混沌系统中，Logistic混沌系统[11-13]是使用频率最高的低维混沌系统。

除了使用混沌系统提高算法的随机性，还可以使用其他原理，比如线性移位寄存器[14]。预先给定一状态的输出，然后将该输出的线性函数再用来做输入的移位寄存器就是线性反馈移位寄存器。对于单比特线性函数来说，异或运算是最为常见的[15]。

为了加强对彩色图像的保护，增强算法安全性的同时，不增加算法的复杂性，本文提出了一种基于混沌和线性反馈移位寄存器的彩色图像加密算法。原始图像使用哈希函数生成密钥流，作为混沌系统的初值。使用给定的密钥多次迭代Logistic混沌系统生成与原始图像大小相同的密钥矩阵。已知密钥作为线性移位寄存器的最初状态，进行多次线性移位也产生一个密钥矩阵。将两种方式生成的密钥矩阵按位异或生成最终密钥矩阵，确保算法的随机性。最终密钥矩阵和原始图像进行异或操作，得到最终加密图像,加密完成。

从以上可以看出，基于混沌理论的图像加密算法具有广阔的应用发展前景。而将混沌理论和线性反馈移位寄存器相结合，生成了更加随机的密钥矩阵，不仅增加了算法的安全性而且也为图像加密提供了另一种方式。

1 基本原理

本章主要介绍本文所使用的混沌映射，线性反馈移位寄存器相关原理。

1.1 Logistic混沌映射

Logistic混沌映射[16]是一个研究时间离散的动力学系统，同时它也是分析混沌、分形等复杂行为的一个非常经典的一维混沌系统模型。Logistic混沌映射是由生态学家R.May用来描述生物种群进化过程的一个经典模型，又名“虫口模型”[17-18]。它的数学定义表达式如下：

xn+1=μxn(1-xn)。

(1)

式中：x是系统参数，x∈(0,1)；μ是控制参数。当μ∈[3.5699456,4]时，混沌系统产生混沌现象，系统迭代生成的值更接近于伪随机分布的状态，Logistic混沌系统的分岔图如图1。

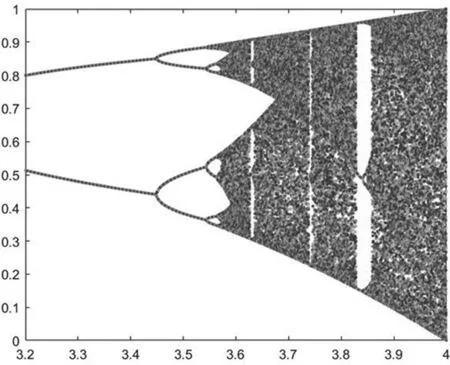
图1 Logistic混沌分岔图

1.2 线性反馈移位寄存器

线性反馈移位寄存器(LFSR)[19]是一种电路结构，由n级触发器以及一些异或门组成。线性反馈移位寄存器也应用于密码学，用于产生加密中使用到的伪随机序列[20]。本文使用线性反馈移位寄存器产生用于加密的密钥矩阵，增强加密算法的随机性。

线性反馈移位寄存器(LFSR)的初值被称为伪随机序列的种子，影响下一个状态的比特位称为抽头。LFSR的触发器编号一般从1开始，抽头取值范围是1到2n-1。LFSR的反馈多项式一般使用抽头序列来描述，n个触发器构成的LFSR可以产生周期为2n-1的序列。线性反馈移位寄存器的具体原理如图2。

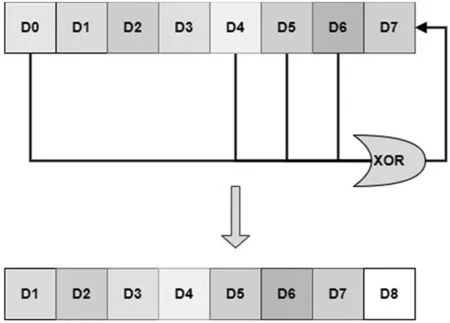
图2 线性反馈移位寄存器原理

从图2中可以看出，将八位二进制中的第一位、第五位、第六位以及第七位异或输出的结果作为原来八位二进制的最后一位，也就是从原始的第二位作为开始，异或得到的二进制位作为结束，形成新的八位二进制。继续以这样的方式线性反馈移位，进而形成伪随机序列。

2 加解密算法

本文提出了一种基于混沌和线性反馈移位寄存器的图像加密算法。本加密算法主要分为三个部分：密钥的生成部分，密钥矩阵的生成部分，原始图像加密部分。具体的加密步骤如2.1～2.3节所示，加密流程图如图3。

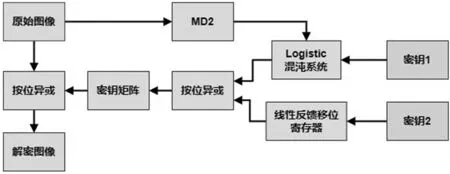
图3 加密流程图

2.1 密钥的生成

原始图像P使用MD2哈希函数生成Logistic混沌的初值，具体操作如下：

第一步：原始图像P使用哈希函数中的MD2函数生成128位摘要信息，表现为32位十六进制字符串D。

第二步：将摘要信息D的每位字符串转化成对应的十进制数值K。

第三步：将K继续进行转换，每个十进制数转换成4位二进制，32个十进制数就转换成128位二进制BK，最后将BK每8位1组转换成1个十进制，总共转换成16个十进制值DK。

第四步：取DK中偶数位对应的值按位异或生成t1,奇数位对应的值按位异或生成t2,为生成Logistic混沌初值做准备，具体如下：

t1=DK{2}⊕DK{4}⊕DK{6}⊕DK{8}⊕DK{10}⊕DK{12}⊕DK{14}⊕DK{16}，

(2)

t2=DK{1}⊕DK{3}⊕DK{5}⊕DK{7}⊕DK{9}⊕DK{11}⊕DK{13}⊕DK{15}。

(3)

其中，⊕是异或操作。

第五步：因为Logistic混沌初值x0∈(0,1)，所以要确保生成的初值在此范围之内。x0生成过程，具体如下：

ts=t1+t2，

(3)

(4)

第六步：所有密钥都已经生成，其中x0作为Logistic混沌初值，Logistic混沌控制参数以及线性反馈移位寄存器的初值状态都是系统直接给定的。

2.2 密钥矩阵的生成

密钥矩阵的生成主要分为三个部分：Logistic混沌映射生成密钥矩阵KM1，线性反馈移位寄存器原理生成密钥矩阵KM2，KM1和KM2按位异或生成最终密钥矩阵KM。

第一步：根据原始图像的大小确定生成的密钥矩阵的大小，其中矩阵长为M，宽为N，维度为O。

第二步：2.1节中生成的x0作为Logistic混沌初值，已知密钥μ0作为Logistic的控制参数，系统迭代M×N×O次，生成M×N×O大小的密钥矩阵KM1。

第三步：使用已知的密钥作为线性反馈移位寄存器的初始状态，进行M×N×O次线性反馈移位操作，也生成M×N×O大小的密钥矩阵KM2。

第四步：将第二步中生成的KM1矩阵和第三步中生成的KM2矩阵按位异或生成大小为M×N×O的最终密钥矩阵KM。具体过程如下：

KM=bitxor(KM1,KM2)。

(6)

其中，bitxor()是按位异或函数。

2.3 加密算法

具体的加密步骤如下：

(1)原始图像P使用MD2哈希算法生成Logistic的初值密钥，增大了密钥空间。

(2)Logistic混沌映射使用(1)中生成的密钥、已知密钥作为初值以及控制参数，生成密钥矩阵KM1。

(3)线性反馈移位寄存器将已知密钥作为初始状态，生成密钥矩阵KM2。

(4)KM1和KM2按位异或生成最终密钥矩阵KM，提高了密钥矩阵的随机性。

(5)将原始图像P和最终密钥矩阵KM进行按位异或操作，生成最终加密矩阵C，完成加密。

2.4 解密算法

本算法的解密算法和加密算法是对称的。需要注意解密过程中使用的密钥应该和加密中使用的密钥一致，以便生成的用于解密的密钥矩阵与加密中使用的一致。另外，需要注意加密对应的解密操作的顺序，以便可以准确无误的解密出原始图形。

3 安全性分析

在win10系统下，使用MATLAB R2020a软件对三组不同的彩色图像进行仿真实验。本算法中一部分密钥与明文有关，另一部分密钥是由系统给定的，本次实验中使用的系统给定的密钥具体情况见表1。参与实验的三组不同的彩色图像包括：Lena图像、Peppers图像以及Mario图像，分别如图4a、5a、6a。本算法得到的三组加密图像分别为图4b、5b、6b，得到的解密图像分别如图4c、5c、6c。

表1 密钥表

a) Lena原图 b) Lena密图 c) Lena解密图图4 Lena图的加密、解密效果

a)Peppers原图 b) Peppers密图 c) Peppers解密图图5 Peppers图的加密、解密效果

a)Mario原图 b) Mario密图 c) Mario解密图图6 Mario图的加密、解密效果

从上述的图像可以看出，本算法可以对内容各不相同的三组图像进行正常有效的加密、解密。以下章节以Lena图为例，对算法的安全性、效率方面展开分析。

3.1 方法对比

本节需要进行三组实验进行对比，其中第一组实验只使用Logistic混沌密钥矩阵作为最终密钥矩阵参与加密过程，第二组实验只使用线性反馈移位寄存器生成密钥矩阵作为最终密钥矩阵参与加密过程，第三组实验使用本算法中的最终密钥矩阵参与加密过程。三组实验的原始图像和加密后得到的加密图像具体如图7～9。

a) Lena原始图像 b) 第一组实验密图图7 Logistic混沌密钥矩阵加密效果

a) Lena原始图像 b) 第二组实验密图图8 线性反馈移位寄存器密钥矩阵加密效果

a) Lena原始图像 b) 第三组实验密图图9 本算法密钥矩阵加密效果

从图7可以看出，只使用Logistic密钥矩阵作为最终密钥矩阵进行加密生成的加密图携带一些图像的有效信息。从图8可以看出，只使用线性反馈移位寄存器作为最终密钥矩阵进行加密生成的加密图不是经典的雪花噪声图，可以看出图像的轮廓信息。图9得到的加密图是经典的雪花噪声图，看不出任何图像信息，可以证明本算法使用的最终密钥矩阵随机性极强。

3.2 密钥空间

只有足够大的密钥空间才可以抵抗密钥暴力破解，从文献[21]可以得知，只有当密钥空间大于2100时才能较为有效的避免被暴力破解。

本算法使用的密钥见表1。其中Logistic混沌系统的初值是由MD2算法和明文图像共同产生的，控制参数是由系统给定的。这一部分的密钥空间为2128+1015。线性反馈移位寄存器的初始状态是由系统给定的，是8个二进制位的数据，这一部分的密钥为28。因此，本算法总的密钥空间为2128+1015+28，大于最低标准的2100。假如每次暴力攻击的时间为1微秒，那么想要破解本算法需要花费大量的时间。因此可以说明本算法密钥空间足够大，保障了算法的安全性。

3.3 信息熵

信息熵用来评估信息源的随机性。信息分布越是有序，信息熵值越低；信息分布越是混乱、随机，信息熵值越高[22]。当信息熵值变高的时候，被非法分子窃取统计型信息的难度会增加，发生的几率会减少。信息熵的公式定义如下：

(7)

式中：n表示图像信息；H(n)表示计算得出的信息熵；ni表示图像n的第i个灰度值；P(ni)表示ni出现的概率；L表示图像n的灰度级。理想情况下，当L=8时，混乱图像的信息熵值为8[23]。

使用表2展现本算法的原始图像以及加密图像的信息熵，并且使用本算法的信息熵与其他文献的信息熵值进行了对比，具体数据见表2。

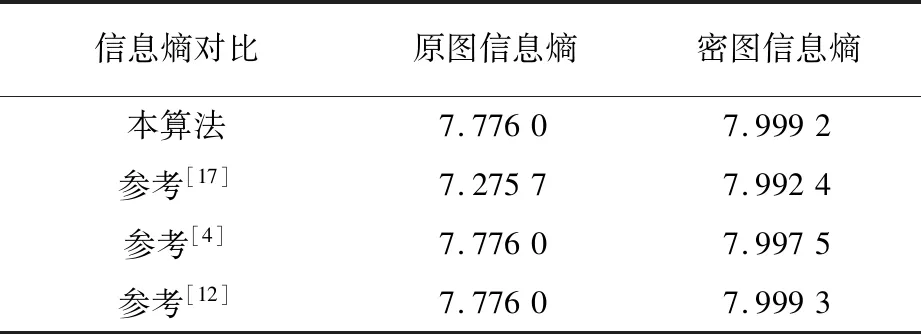
表2 信息熵对比表

本表展示Lena图像的原图的信息熵以及密图的信息熵值。原图的信息熵与理想值有一定的差距，经过加密后的密图的信息熵为7.999 2，该值十分接近于8。其他参考文献的密图的信息熵值也接近于理想值，加密效果良好，但相比本算法的信息熵值略低。因此可以说明本算法可以有效地将图像的信息熵值变高，降低了算法被统计性攻击的风险。

3.4 直方图

图像像素值的分布概率可以用直方图来表示，它描述了一幅图像灰度值的统计相关性[24]。因此判定一个算法的性能好坏是可以从直方图看出的。通常来说，如果图像灰度值分布越均匀，抵抗统计攻击的能力就越强。原始图像Lena的直方图如图10a，加密图像的直方图如图10b，解密图像的直方图如图10c。

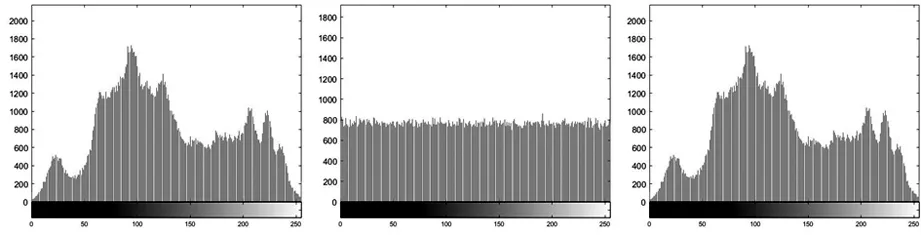
a) 原图直方图 b) 密图直方图 c) 解密图直方图图10 原图、密图、解密图的直方图

从图10可以看出，明文图像的像素点值一般来说是集中分布的，呈现一种高低起伏的状态。而加密图像的直方图则是均匀分布的，这说明通过加密图像直方图是不可能得到任何有用的统计信息的，更进一步说明攻击者是无法通过加密图的直方图获取到明文图像信息的。

3.5 相关性

相关性系数能够反映出相邻像素的相关程度[25]。通常来说，明文图像中相关性较强的是对角线、垂直、水平方向上的相邻像素点，但是这种相关性在加密图像上是没有显著体现的。相关性系数越小，相邻像素的相关性也越低，就越容易抵抗统计分析攻击。相关性系数数学表达式如下：

(8)

9)

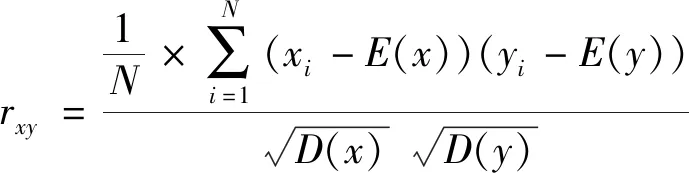
(10)

式中：E(x)是期望值；D(x)是方差；(x,y)都是图像的相邻像素对；rxy是相邻像素对的相关性系数。在理想情况下，希望相邻像素对不存在相关性，也就是理想相关性系数值为0。表3～5分别展示了随机取2 000对相邻像素对进行实验得出的R、G、B通道的水平、垂直、对角线方向的相关性系数情况。各个方向的相关性点图如图11～13。

表3 原图、密图R通道相关性系数表

表4 原图、密图G通道相关性系数表

表5 原图、密图B通道相关性系数表

Lena图加密前后R、G、B通道3个方向的相邻像素相关性结果见表3～5。从表中可以得出，原始图像相邻像素相关性系数接近于1，加密图像相关性系数接近于0，说明本算法可以非常好的降低相邻像素相关性，在抵抗统计攻击方面效果良好。同时在表3～5还给出了与最新文献加密图像相关性系数的对比结果，可以看出本算法在降低相关性方面表现更为突出。另外，从图可以看出原始图像3个通道不同方向的相关性点图中像素分布呈一定的正相关，而密文图像3个通道不同方向的相关性点图像素呈现离散状态，更趋于均匀分布。

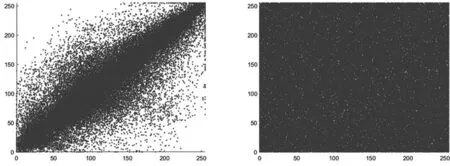
a) 原图水平 b) 密图水平图11 水平方向相关性点图

3.5 时间分析

时间性能是衡量图像加密算法时效性的重要指标[26]。在实际应用中，图像加密算法既要保证具有良好的加密、解密效果，也要保证运行时间在可以接受的范围之内。本实验在个人计算机中使用MATLAB 2020a软件对三组内容不同的彩色图像进行了时间测试，测试结果见表6。

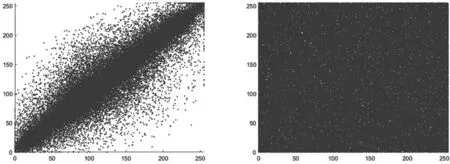
a) 原图垂直 b) 密图垂直图12 垂直方向相关性点图

a) 原图对角线 b) 密图对角线图13 对角线方向相关性点图

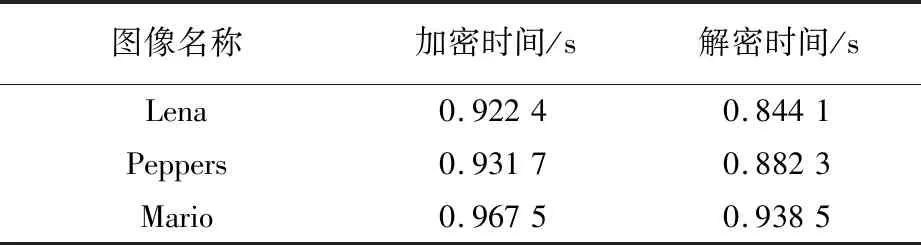
表6 时间性能对比表

从表6可知，三组实验中加密、解密时间较长的为0.967 5 s，也就是三组不同的彩色图像加密和解密时间都控制在1 s之内。因此可以表明本算法在加密、解密的运行时间方面有一定的优势。

4 总 结

本文提出了一种基于混沌和线性反馈移位寄存器的彩色图像加密算法。采用Logistic经典混沌系统与线性反馈移位寄存器相结合的方式生成参与图像加密的密钥矩阵，不仅提高了加密算法的安全性，还保证了算法的随机性。为了提高明文与密钥之间的关联，增强抵抗已知明文攻击的能力，本算法的原始图像使用MD2哈希算法生成密钥。原始图像和密钥图像采用按位异或的方式进行加密，加密结束，得到加密图像。从仿真实验、方法对比以及安全性分析结果可知，本算法的密钥空间足够大，加密、解密效果良好。另外算法在运行时间方面有着一定的优势，适用于彩色图像加密。