基于杂草算法的配电网光伏电源优化研究

李飞

（德州职业技术学院 山东省德州市 253014）

考虑到光伏电源分布较广，进而增加了电网的复杂度。因此，加强配电网光伏电源的优化配置，对提高电网的运行效率具有非常重要的价值和意义。而针对光伏电源配置优化问题，黄炜等从配电网规划的角度，提出在保障电压质量的条件下，对负荷和分布式光伏电源沿10kV 线路接入位置及容量进行了匹配，对其形成的组合进行计算，得到了不同组合下和实际情况更严格的分布式光伏电源接入的容量区域，以此来为后期对光伏电源接入配电网提供了科学的依据[1]。洪坤伟又在对分布式光伏发电规划方案中，有针对性的对电能质量进行了考虑，并且做好了负荷预测和设备的选择，再依据分布式电源容量的原则设计了相应的配置方案，以提升接入电网的质效[2]。王磊等对接入节点的光伏电源的特点以及节点净负荷等进行了相关研究，利用FastUnfolding 聚类算法对光伏电源集群进行划分[3]。上述研究中，对光伏电源的配电网规划做出了正确规划，也分析了光伏电源的一些特点，但是如果要构建出一个可行的光伏电源配置多目标模型，仍然需要进一步的研究和改进。

1 光伏电源配置多目标函数

1.1 目标函数构建

考虑到光伏电源渗透率和配电网损耗问题，也要对配电网的相关要求和光伏电源接入的影响，将这些作为目标优化模型的约束条件。通过权值系数，将多目标优化问题转化成单目标优化问题，公式调整为：

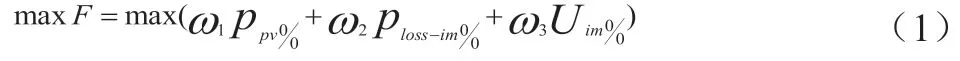
1.2 约束条件

约束条件包括潮流约束、电压约束、电流约束和配网保护约束。其中，

配电网内潮流的约束条件为：

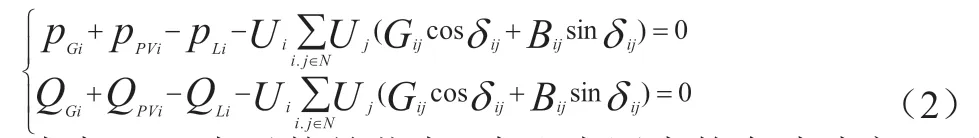
式中，PGi表示的是节点i 在配电网中的有功功率，而QGi表示的则是其无功功率；Ppvj，Qpvj代表了光伏电源为其提供的一个有功和无功功率的大小状况。其中的有功和无功负荷用的是PLi、QLi进行表示，节点电压的一个大小变化值也就是幅度值由Ui和Uj分别进行表示；节点i 和j 之间的相位角之差、导电率、电纳分别用δij、Gij、Bij来进行表示。

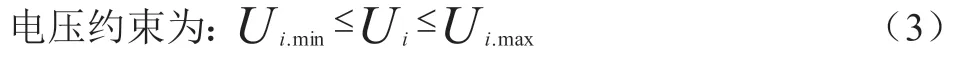
式中，Ui.min是节点i 在此处的一个电压可以允许的最小值， Ui.max则是节点i 在此处的电压可以达到运行的最大值。

馈线允许的最大电流大小为：

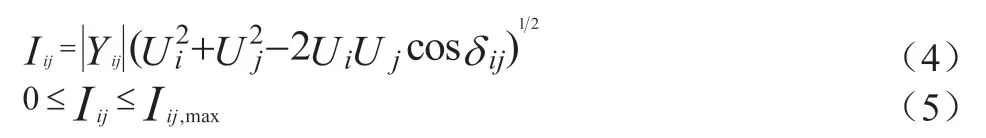
式中，Yij表示的是导电率，Iij是馈线节点i 和节点j 之间的电流，Ui和Uj是对各自节点的一个电压变化幅度的范围，节点i 和节点j 之间的相位角只差在公式中用的是δij来进行表示，而两节点之间的电流最大值用Iij.max进行表示。

光伏电源接入容量约束满足：

式中，第i 个光伏电源接入容量用Ppvi进行表示；最大光伏电源接入容量用Ppvimax进行表示；接入光伏电源的总数用M 表示；Ppvi是第i 个光伏电源接入容量；其中的负荷总数量是用N 表示。

配电继网保护的约束条件为：

2 目标函数的求解

2.1 杂草算法

杂草算法是一种简单而又高效的智能算法，参数少，自适应力强，因此被广泛的运用于解决多目标的优化问题中。杂草算法的具体流程如图1 所示。

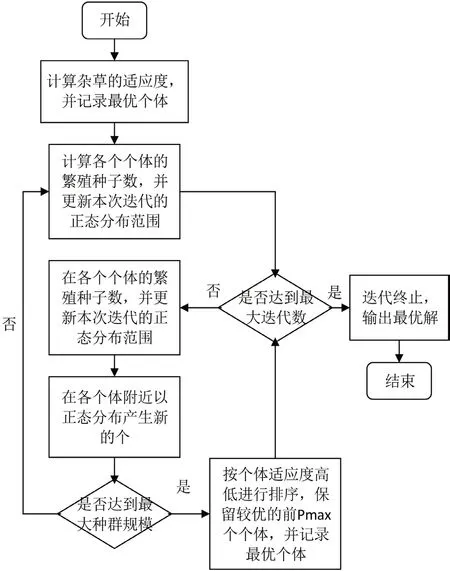
图1：杂草算法流程

2.2 杂草算法的改进

杂草算法仍存在着对于初始参数设置敏感，搜索全局空间能力弱的问题。解决这两个问题可以在杂草算法的初始化状态和扩散的过程中加以改进，进行改进后可以使得杂草算法对于全局空间的搜索能力加强，同时还可以加快收敛速度。

2.2.1 分散播种

经过观察和研究，杂草的生成位置虽然在初始阶段是随机的，但是分布区域是有规律的。如图2 所示，在杂草算法初始时，杂草在1,2,3,4 区域中，种子根据杂草位置扩散后会在各个区域进行分布，使其分布具有多样性。但是，如果只是随机生成杂草，杂草仅分布在1,2,3 区域，那么杂草种子的范围就不会在4 区域上。这样就会在算法执行过程中搜素不到4 区域，便得不到最优解。

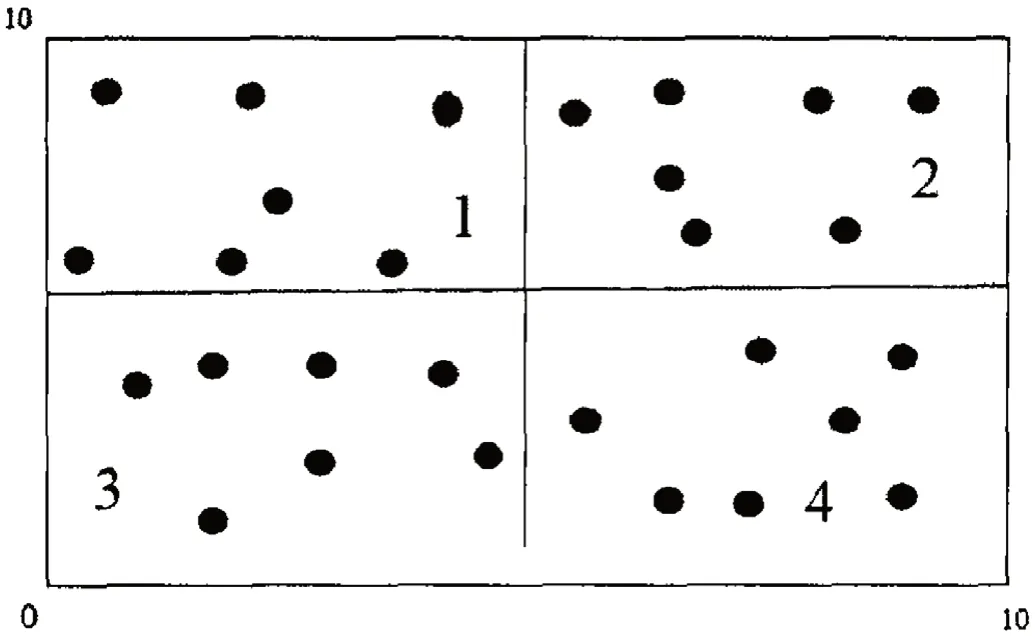
图2：分散播种示意图

要使种子的分布区域呈多样化趋势，使得杂草位置在初始化阶段的分布不能集中在同一个区域，因此需要在算法初始化阶段，就使杂草要在每一个区域都有所分布，就可以使算法在运行中对全局求解空间进行搜索，然后形成最优解。

2.2.2 添加混沌扰动量

杂草算法中的种子扩散范围是由正态方差分布得到的，其范围与杂草的初始位置有较大的关系，而杂草初始位置会集中在同一侧，不跳出这个区域，就不能得到最优解。为解决这问题，需利用种子扩散过程中的启发性信息来对种子扩散进行引导，保障种子的多样性，使算法尽快收敛。在种子扩散范围方差时，加入Logistic 扰动量控制方差变化。因为混沌理论具有随机、非周期和遍历的特性，可解决杂草算法多样性不足的问题。

在加入Logistic 扰动量后，杂扩散公式变为：

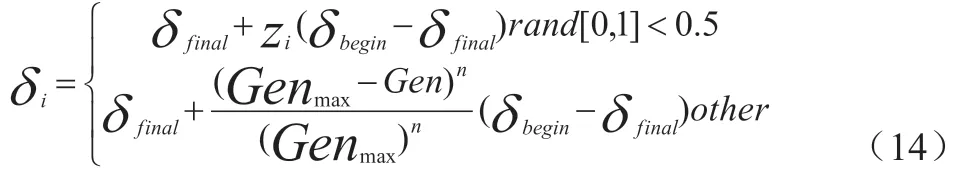
式（10）中，rand[0,1]表示的是产生区间0 到1 的随机数，当这个随机数小于0.5 的时候，就会利用混沌扰动来计算正态分布扩散的方差，而这个随机数大于0.5 的时候，则是利用以前的扩散公式来计算。

2.3 混沌杂草的求解步骤

利用改进的杂草算法求解多目标优化问题，具体的步骤如如图3 所示。

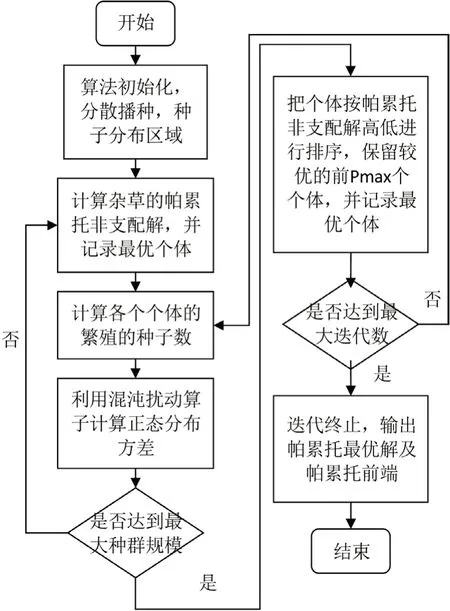
图3：混沌杂草算法求解多目标函数的流程

3 仿真验证

3.1 参数设置

将利用多个函数来对两种算法进行测试，验证改进后的算法是否比杂草算法具有更好的效果。在测试中，两种算法将采用相同的参数来保证测试的公平和准确性。具体参数为迭代次数N=100，初始杂草数P0=10，杂草最大数Pmax=25，种子最大数Smax=10，种子最小数Smin=4，正态分布方差最大值为20，正态分布方差最小值为1。

3.2 测试函数及测试结果

测试过程中使用到的函数是从标准函数库中挑选Fl 和ZDT1。每个函数都会运行30次。最终的测试结果如表1所示。

表1：测试结果

从表2 可知，改进杂草算法的最优值、最差值、平均值都是优于标准杂草算法的。要使得杂草算法对整个求解空间都进行搜索可以通过分散播种和添加混沌扰动量这两个步骤来进行实现，并且增大了杂草算法，使搜索最优值更快速。因此改进杂草算法的搜索能力和收敛精度都是高于标准杂草算法的，收敛速度也更快。从图4 和表2 可知，改进后的杂草算法和标准杂草算法相比，多目标算法的各项性能都得到了一定的提升，在ZDT1 和ZDT2 问题的测试中，可以得到改进后的杂草算法的解更具多样性和稳定性。该实验结果表明，改进杂草算法是具有更高的收敛速度和搜索全局的能力的。

表2：单个光伏电源优化配置结果

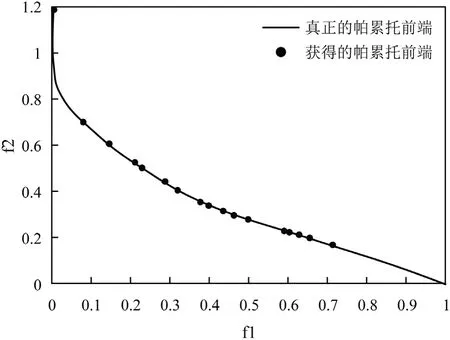
图4：函数ZDT1 的适应度函数进化曲线

3.3 算法应用验证

3.3.1 IEEE33 节点系统

将利用改进杂草算法对配电网优化配置的多目标优化模型进行验证，以此证明优化结果的准确性。

城市里都是采用的以单源辐射状链式结构的配电网，IEEE33 节点的配电网的结构如图5 所示。

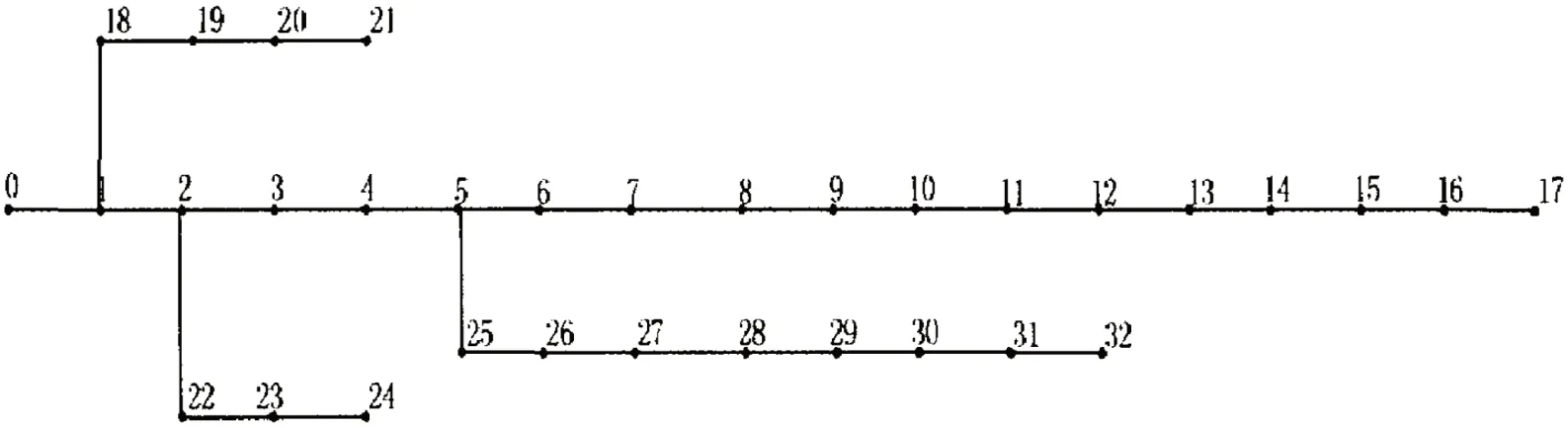
图5：IEEE33 节点结构图

IEEE33 节点的配电网中一共有33 个节点，其中的节点0 是原系统节点。

为了更好的提升配电网的电能质量，在光伏电源接入配电网的位置，应该接近配电负荷的中心。为了使该模型更加简化，将光伏电源假设接在了IEEE33 配电网的负荷节点，控制光伏电源在一个稳定的条件下工作，把工作时的有功输出和无功输出的变化波动不断减小。电源节点是在在配电网潮流计算中，把光伏电源作为负荷节点处理，然后去掉负值。功率因数设置成了0.95，以便简化其中的计算过程。

3.3.2 单个光伏电源优化配置的求解

对接入到配电网中的光伏电源容量进行一个设置，最小值设为100KW，最大值设置为1MW。而光伏电源的接入点也是有选择依据的，要充分的考虑到母线情况和最大负载，并且还要去尽可能的避免反向潮流。改进杂草算法运行的具体参数与上面一致。光伏电源的渗透率的权值系数是0.5，配电网损耗的权值系数是0.25，电压改善率的权值系数是0.25。通过求解，得到单个光伏电源节点的最优配置，具体如表2 所示。

IEEE33 算例是以光伏电源的多目标优化配置模型为基础来进行了建模，然后利用改进杂草算法进行求解，结果如上表所示，通过该表可以得出，改进杂草算法在各个方面都是优于标准杂草算法的，例如渗透率、配电网损耗改善率、电压改善率。

3.3.3 多个光伏电源优化配置的求解

对接入到配电网的光伏电源容量的设置和上文中单个光伏电源优化配置中的设置参数一样。接入的个数为4，每一个的容量不能超过400KW，总容量最大值是1MW。考虑情况和上述的光伏电源的待选接入点同单个光伏电源优化配置一样。通过求解得到最优配置结果如表3。

表3：多个光伏电源优化配置结果

通过表3 可知，对于光伏电源，改进杂草算法的渗透率、配电网损耗改善率、电压改善率等指标的最优值均优于标准杂草算法。优化的最终结果表明，优化配置模型是有一定的准确性的，因此所提出的改进杂草方法在含光伏电源的配电网优化配置问题上具有可行性。

4 结语

综上，为合理的选择光伏电源的容量和接入位置，减少对光伏电源的不利影响，首先提出了光伏电源优化配置的多目标模型，对光伏电源渗透率以及配电网损耗等作了充分的考虑。然后引进了杂草算法并根据实际情况做出了分散播种和添加扰动量的改进，改进后的杂草算法在收敛速度和全局搜索能力上都得到了一定的提升，但仍还存在一些问题，如没有在实际中考虑到配电网的运行指标和光伏电源的暂态特性，并且实际中的配电网结构更为复杂。这些问题都还需要不断的进行研究和改进。