无线传感网络分段线性融合定位算法*
李 锋,魏楚强
(广东交通职业技术学院,广东 广州510650)
0 引言
无线传感网络是一种由大量传感节点构成的无线多跳式自组织网络。由于节点采集到的环境信息通常与其自身位置相关,如何实现对节点的精确定位是其首要解决的关键问题[1]。在三维立体空间中,要实现对未知节点定位,至少需要三个立体空间锚节点坐标[2]。基于此原理,业界提出三维跳段距离向量3D-DVHop算法、基于接收信号强度的RSSI-3D算法、近似球形内点测试APIS-3D算法和近似三角形内点测试APIT-3D算法等。在以上经典算法中,3D-DVHop算法定位原理与二维平面类似,会因相邻节点接力的“绕弯”现象[3]导致平均跳距误差较大,定位精度较低;RSSI-3D算法将未知节点采集到的指纹特征与数据库进行最近匹配以估算节点坐标,但RSSI接收信号强度易受环境信号波动和多径衰减影响[4],定位结果随机性较大;APIS-3D算法利用节点自身存储本地位置信息,定位精度对节点密度依赖过大[5],当节点分布不均时定位精度不高;APIT-3D算法通过计算四面三棱椎体重叠区域质心来计算节点坐标,算法成熟,平均定位精度较高,但容易陷入“In-To-Out”和“Out-To-In”[6]两类内测点测试错误,导致边缘节点定位偏差较大[7]。根据APIT算法,目的节点需要判断是否处于其附近任意三个锚节点所组成的三角形中,“In-To-Out”和“Out-To-In”错误就是目的节点对所处三角形区域的两种误判形式。
由于三维空间定位比传统二维平面复杂很多,算法目前尚属改善阶段[8],无法在移动环境中对节点进行精确定位[9]。然而,传感节点会随机部署在某一三维区域,并会随周围环境变化而变换位置。如何在现有二维平面定位算法基础上,延伸至三维空间,并对其内移动节点精确定位,是目前无线传感网络研究的难点。
有鉴于此,本文提出一种基于APIT-3D的移动节点定位模型和算法,综合3D-DVHop跳段距离和RSSI测距技术,在计算内测点与最近椎面距离基础上,利用与椎体成形体积判断内测点位置,有效避免“In-To-Out”和“Out-To-In”两类错误的产生。在确定椎体重叠区域后,通过最小二乘法结合空间分段线性融合方式计算节点位置,判断运动趋势,描述运动轨迹,实现对移动三维节点的精确定位。
1 分段线性融合定位算法对内测点的判断
在APIT算法中,当邻近节点较疏或不能组成三角形时会导致内测点判断错误,即“In-To-Out”与“Out-To-In”两种错误类 型[10-11]。APIT-3D算 法将传统的二维平面延伸至三维立体空间,同理也会导致上述错误。本文分段线性融合定位算法通过内测点与椎体成形体积判断其位置,从而避免上述两种错误类型的产生,解决方案和步骤如下:
引入RSSI信号衰减模型计算内测点N与四面椎体ABCD之间距离。RSSI衰减模型为:

式中,RSSI(d)为距离源节点d处接收到的信号强度,RSSI(d0)为距离源节点d0处测到的信号强度值,df为内测点与障碍物之间距离,ΣWAF为标准偏差和。
为减少相邻节点因接力“绕弯”导致的误差,采用平均跳距增益η对节点通信距离进行修正,η为平均跳距和节点平均通信半径之比:

利用跳数增益修正内测点与四面椎体顶点之间的参考跳距:
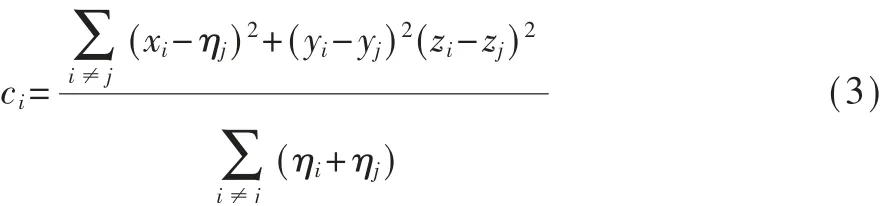
则椎体顶点锚节点i与内测点N之间参考跳距为:

设hopsij为锚节点i到j之间的跳数,则通过未知 节 点N测 得 从 锚 节 点A,B,C,D收 到 的RSSI值,转换为参考跳距为:

在计算出内测点N与四面椎体顶点锚节点参考距离基础上,通过平面夹角三角函数计算N与椎体最近平面的最短距离为:

利用内测点与椎体成形体积判断其位置,见图1所示。若内测点N在四面椎体ABCD内,则其与椎体四面组成的体积与四面椎体ABCD体积相同;若N在四面椎体外,其与椎体四面组成的体积必定大于四面椎体ABCD体积。因此,判断内测点N是否在椎体内部的问题,可以转换为求以ΔACD为底,BH和BN为高的多面体体积上。当BH≤BN时,内测点N在四面椎体内部,反之则在椎体外部,从而避免APIT-3D算法中内测点误判现象。
2 静止节点定位方式
为实现无线传感网络对目的静态节点的定位,内测点判断完成后,通过计算重叠区域质心获得目的节点位置。设邻居节点数量为n,依次与未知节点组成四面椎体,共有种组合。判断所有组合中内测点与四面椎体的位置关系,确定内测点在椎体内部的所有三棱椎体重叠区域,利用网格扫描计算区域质心,如图2(a)所示,则未知节点坐标为:

其 中,X,Y,Z分 别 为 目 的 节 点 在x轴,y轴 和z轴坐标,xa,xb,xc,xd分别为有效三棱锥的四个锚节点的x轴 坐 标,ya,yb,yc,yd分 别 为 有 效 三 棱 锥 的 四 个锚节点的y轴坐标,za,zb,zc,zd分别为有效三棱锥的四个锚节点的z轴坐标,RSSIa,RSSIb,RSSIc,RSSId分别为目的节点接收到的锚节点信号强度。
3 分段线性融合定位算法对移动节点的定位
3.1 定位过程
受环境影响,无线传感节点位置处于不断变化中[12-13]。在确定重叠区域和节点位置后,分段线性融合定位算法利用最小二乘法结合空间分段线性融合方式判断节点运动趋势,即将节点曲线运动看成是多个分段直线运动的叠加,从而描述运动轨迹,如图2(b)所示。设k时刻未知节点(xk,yk,zk)所在的第一段空间直线标准方程为:

式 中,k-1为k时 刻 的 上 一 时 刻,(xk-1,yk-1,zk-1)为目的节点在k-1时刻的坐标。
空间直线在XZ平面投影方程为:


为达到差值最小,将a、b、c、d取值为方程系数,满足关系:

根据式(10)和式(11),有:

其 中,A=[a b]′,X=[x1,x2,…,xm]′,B=[c d]′,Y=[y1,y2,…,ym]′。
求解m组数据点集方程组,得到融合直线参数a、b、c、d值[14]。
同样原理,在k+1,k+2,…,k+n时刻对目的节点测得的三维坐标分别为(xk+1,yk+1,zk+1),(xk+2,yk+2,zk+2),…,(xk+n,yk+n,zk+n),分段线性融合定位算法在三维空间对直线融合并预测节点移动方向和速度,以此更新融合直线参数a、b、c、d值,从而确定曲线方程。
3.2 算法流程图
本文提出的分段线性融合定位算法,通过穷尽各目的节点与邻居节点组合形成的四面椎体,基于测距算法计算目的节点与椎体之间距离,利用与椎体成形体积判断内测点位置,将底高大于距离的三棱锥作为有效三棱锥,计算其质心坐标。最后,在确定椎体重叠区域后,通过最小二乘法结合空间分段线性融合方式计算节点位置,得到所述目的节点运动轨迹,整个流程如图3所示。
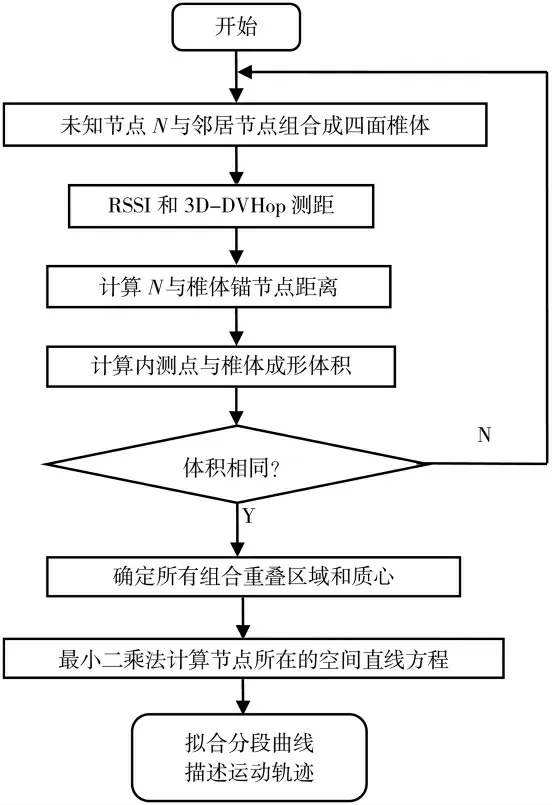
图3 分段线性融合定位算法流程图
3.3 定位误差分析
假设三维空间中,目的节点N距网络锚节点i、n实际距离分别为估算距离分别为di和dn,则:

在式(15)中,将n和n-1分别带入参数n中,求得第n和第n-1项表达式,并计算n项-(n-1)项:

则未知节点定位误差为:

4 仿真测试
4.1 静态节点定位偏差测试
将锚节点随机部署在l00×l00×100三维立体空间内,最大锚节点上限数量为100,节点通信半径为20,为让测试环境更贴近实际工程,随机产生DOI信号扰动系数[0,0.65],利用MATLAB7.0软件对算法仿真比较,如图4所示。从图中可以看出,四种算法定位误差伴随锚节点密度增加而减少。由于节点非均匀分布,3D-DVHop在计算平均跳距时因节点“绕弯”路径复杂,定位偏差最大;RSSI-3D易受电磁环境和信号波动影响,曲线扰动明显,若增大DOI信号扰动系数则会进一步加大定位误差,在复杂电磁环境影响下尤为明显;而本文提出的分段线性融合定位算法能有效避免APIT-3D导致的内测点测试错误现象,根据式(16)、式(17)计算平均定位偏差为1.76%,算法优势明显。
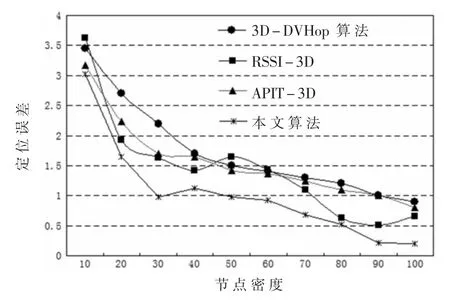
图4 静态节点定位偏差图
4.2 移动节点定位偏差测试
由于其余三种算法不能在三维环境下对移动节点定位,文章只对本文分段线性融合定位算法进行测试,结果如图5。未知节点数量为100,在区间[0,5]随机初始化节点移动速率,根据式(16),节点在百分之25th,50th和75th定位偏差值分别是1.81 m,2.45 m和3.32 m,平均偏差为2.26%,如表1所示。

图5 移动节点定位偏差图

表1 移动节点定位偏差表 (m)
4.3 移动节点轨迹模拟
锚节点数量为100,引入虚拟力场在x、y、z方向随机赋予未知节点牵引力度,时间间隔k=1 s,分段直线运动融合后曲线轨迹如图6所示。

图6 移动节点轨迹模拟图
5 结论
本文提出一种基于APIT-3D的移动节点定位模型和算法,解决无线传感网络中边缘节点定位精度不高的问题,并能判断运动趋势,描绘运动轨迹,为三维环境下节点定位提供算法借鉴和创新。由于多个信号源电磁波在传播时会产生反射、绕射和散射现象,影响定位精度和跟踪准确率,下一步工作将着眼于在复杂电磁环境下实现对目的节点的精确定位。
——以徐州高层小区为例

