基于AHP-熵权法的平原城市河网水系连通性评价——以廊坊市为例

梁霄，巨文慧，孙博闻，胡泽，高学平，张晶，赵进勇

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300350；2.生态环境部环境规划院，北京 100012；3.中国水利水电科学研究院，北京 100089)

城市化进程影响着水系的结构特征和空间分布[1]，由人类活动引起的水系衰减、水面率下降、支流退化以及河网复杂度下降等因素显著影响着城市水系的蓄滞洪能力、水环境健康和水文过程。水系的功能与水系连通程度存在密切联系[2]，具体表现为：水系连通促进物质的迁移转化，为能量流动提供基本场所；水系连通能够维持河湖生态演化功能[3]。目前对水系连通性尚未形成统一定义，依据应用广泛程度采用长江水利委员会在《维护健康长江，促进人水和谐研究报告》中对水系连通性的定义：河流干支流、湖泊及其湿地等水系的连通状况，反映水流的连续性和水系的连通状况[4]。因此，对平原城市河网水系连通性评价展开研究具有重要意义。

国内外已有研究多基于水系形态、图论与水文过程的某些指标进行评价，评价指标包括水系格局、结构连通性和水力连通性3个方面。其中，水系格局与结构连通性两方面指标应用较多，而水力连通性研究相对较少。

在水系格局与结构连通性评价方面的研究有：Cui等[5]基于图论理论从结构连通性方面对比分析高流量和低流量两种城市河网的水系连通性；周振民等[6]从水系格局和结构连通性两方面选取部分特征指标构建城市河网水系结构评价体系，分别对规划前后的郑州市河网水系连通性进行评价；窦明等[7]从水系的结构形态和连通形态两个层面构建了一套描述水系形态演变特征的评价体系，并对郑州市水系进行实例应用；夏敏等[8]对表征河网连通程度的主要指标进行了概括，得到水系格局连通度，在此基础上综合结构连通性指标构建评价体系，对巢湖环湖区水系连通性进行评价；傅春等[9]建立水系格局与结构连通性评价体系，对城市化进程下南昌市城区水系特征变化与河流连通性进行初步探讨；李普林等[10]从水系格局和结构连通性角度出发，选取6项指标建立水系连通性评价体系，对研究区水系规划前后进行连通性评价；马栋等[11]基于图论边连通度方法，从结构连通性方面对扬州市主城区水系结构连通状况进行评价。

在水力连通性评价方面的研究有：孟祥永等[12]在水系格局和结构连通性基础上增加水力连通性评价内容，构建区域尺度下城市水系连通性评价体系；Phillips等[13]建立基于水流阻力及水文过程的城市河流水力连通性评价体系；崔广柏等[14]综合考量平原城市河网的水系特点，从水系格局与水力连通性等方面选取较为关键的指标构建水系连通性评价体系；李景保等[15]从结构连通性方面构建水系连通性评价体系，并以水位为研究对象，增加水力连通性方面评价内容，从结构连通性和水力连通性两方面综合分析研究区水系连通变化过程。

以上对于平原城市河网水系连通性评价的研究，不同学者侧重点均有不同，目前并未系统地构建水系连通性评价体系。由于平原城市河网水系密布，在闸门、水泵等水利工程的控制下，水流运动复杂，水系连通不畅，影响河道自净能力[14]。同时，影响水系连通的因子是多样的，闸坝的调控使其影响更具不确定性。因此，对于平原城市河网的连通性评价在考虑水系格局和结构连通性基础上还需要考虑水力流动性，从而更为科学地分析评价城区水系的连通状况。基于此，本文以廊坊城区水系为例，选取能够代表城区水系连通性的关键因子，从水系格局、结构连通性、水力连通性3个方面构建平原城市河网水系连通性评价体系，定量评价不同水系连通方案的水系连通状况，确定最优水系连通方案。

1 研究区域概况与数据来源

1.1 研究区域

研究区为廊坊市区(广阳区、安次区)，包括整个未来规划区中心城区、都市区北部，总面积942 km2，地处永定河冲积平原，属于平原河网区，以平原和洼地为主，自北向南倾斜，海拔0～20 m，地势平缓。区域多年平均气温11.8 ℃，年平均蒸发量1 909.6 mm，年平均日照2 689 h，日照率为60%。区域内主要河流包括北部的凤河、中部的龙河以及南部的永定河，其中环城河流包括五干渠、六干渠等8条支渠。永定河泛区河流包括天堂河、胜天渠等6条支渠，见图1。区域内水量分布不均，其中北部的凤河水量丰沛，而中部的环城河道、龙河、南部的永定河泛区缺水严重，龙河出境处多年断流，泛区断流30年以上。因此，有必要对该区域制定合适的水系连通方案，通过构建水系连通性评价体系对不同连通方案的水系连通性进行分析评价，以得到该区域水系连通最优方案，从而缓解该区域水资源短缺等问题，提升廊坊城区水资源均衡程度。

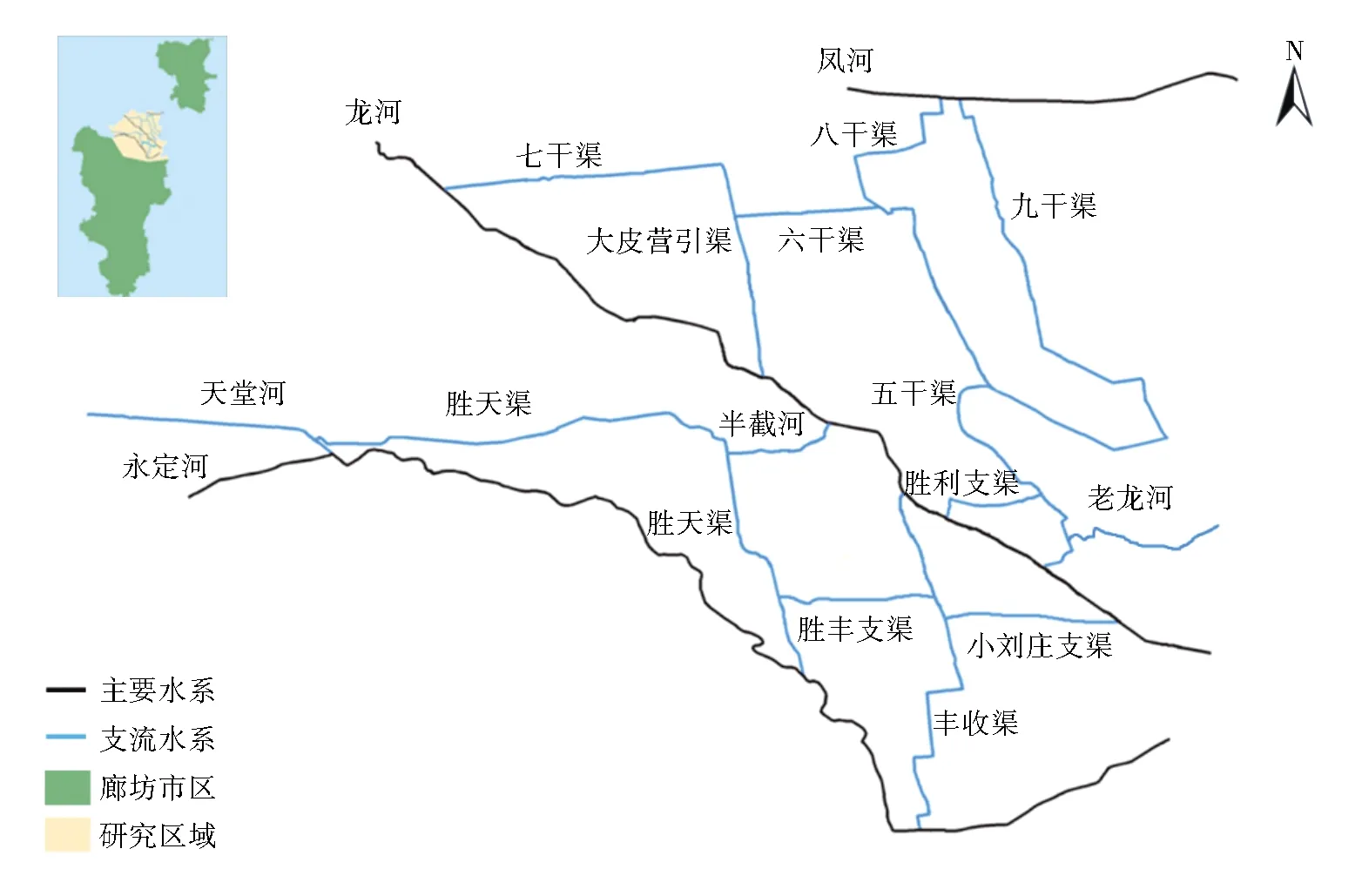
图1 研究区域河流水系

1.2 数据来源

廊坊市河网水系的河道特征、水文参数、水力特性、闸坝过流能力等数据来源于《廊坊水文水资源实用指南》《廊坊市生态水系总体规划(2016—2030)》《2019年廊坊市水资源公报》《廊坊市河道等级分类表》等相关资料。

2 研究方法

2.1 水系连通性评价体系构建方法

城市水系是一个复杂的水网系统，为描述城市水系不同连通方案的水系连通状况，需构建一套评价体系对城市水系连通性进行评价。选取国内近年来几个代表性的城市水系连通性评价研究案例，对其指标选用进行总结，发现对于水系连通性评价指标的选用较为复杂，不同学者侧重点有所不同，详见表1。其中：水系格局方面主要是以河网密度来描述区域水系的河流特征，水面率和河频率的选用也相对较多[6,9,11]；结构连通性方面更多基于景观生态学和图论理论进行评价，主要采用水系连通度指标来评价水系的结构连通性[8,12]，部分学者基于河流分级标准[9]或从定性角度[14]采用能够反映河道自身结构属性的指标，以衡量水系结构连通性强弱；水力连通性方面只有个别学者有所涉及，指标选用也相对欠缺，几乎忽略了水力连通性对城市水系连通的影响。为定量评价平原城市河网的水系连通状况，根据城市水系特点对表1中各准则层相应的指标进行筛选或改进，构建一套适合平原城市河网的水系连通性评价体系。为提高城市水系连通性评价体系适用性、兼顾资料获取难易等情况，将表1中评价指标按照使用频率进行排序后分为必选指标与可选指标，方便在不同研究区域进行评价时能够灵活选取。考虑到水力连通性对河网水系的影响，建议在构建水系连通性评价体系时至少选取一个水力连通性指标。

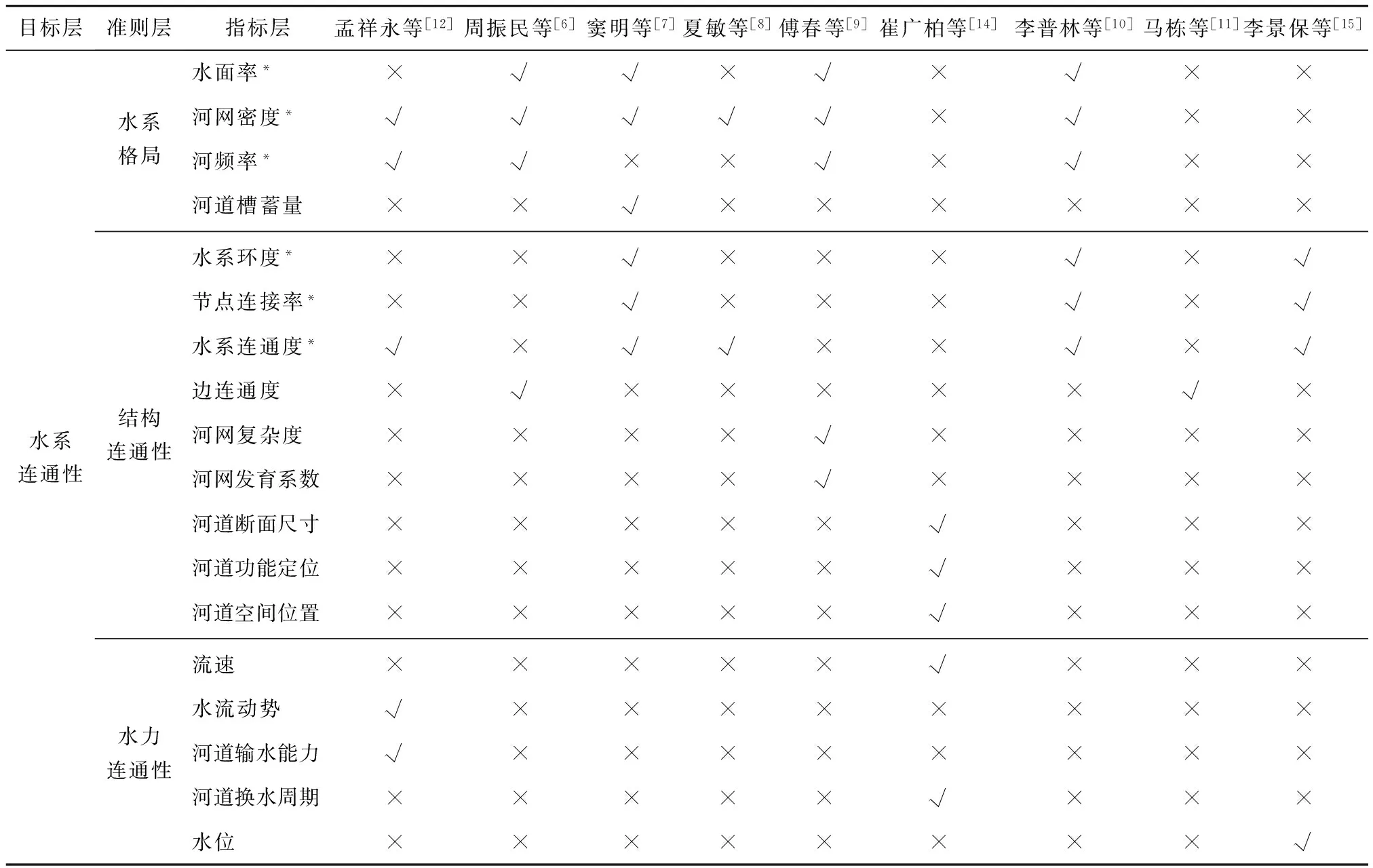
表1 城市水系连通性评价体系指标

2.1.1水系格局评价

现有的水系格局指标主要从河流地貌学等角度出发，采用河网密度、水面率、河频率反映水系的形态特征。河网密度、河频率分别表示单位面积上河流的长度和数量，水面率反映区域水域面积的大小，3项指标虽能表征区域的水系规模，但侧重点均局限于静态的反映水系的发展现状。对于动态评价方面，如河道能否发挥其容蓄洪水的作用等方面有所欠缺，导致目前人们改造城市河流水系对河网产生的负面影响存在很多未知。城市水系不同于一般水系，在城市发展建设的同时应重点兼顾城市水系防洪排涝等问题。河道槽蓄量是评价河道防洪排涝能力的重要指标，可以直接反映河网容蓄洪水量及水资源调度能力[16]。鉴于此，在静态评价基础上增加动态评价，计算河道槽蓄量。综合考虑静态和动态两方面因素，选取水面率、河网密度、河频率和河道槽蓄量[6,8,12]4项指标，更全面地评价城市水系的形态特征。

2.1.2结构连通性评价

平原城市河网水系密布、水流运动复杂，并且地势平坦、河道水流流向不定，加之城市水系人工改造程度高，不符合Horton、Strahler等[17]提出的河流分级规律，而人为根据河流宽度进行水系分级时主观性较强，并且缺乏足够的经验，因此采用基于河流分级准则的河网复杂度、河网发育系数等指标来评价平原城市河网水系结构连通性明显不足。图论理论中边连通度主要适用于分析同一研究区不同年份河网连通性的变化特征[6]；崔广柏等[14]只侧重于从定性角度分析河道级别的高低。为将结构连通性以量化形式体现，引入网络结构连通性，其来源于景观生态学中景观生态网络连接度的概念[18]，依据图论理论[19]对区域河网内水系进行结构连通性评价。目前，多指标评价法是景观生态网络连接度的常用评价方法，依据网络结构中“点-线”的数量关系来评价结构连通性。景观生态网络连接度一般采用节点度数、廊道密度、水系环度、节点连接率和水系连通度等指标，节点度数一般不用于水系连通，廊道密度等同于水系格局准则层下的河网密度[20]，加之城区河网水系复杂，网络结构中点、线数量较多，在选取指标时应将点与点、线与线、点与线之间的关系对网络结构的影响因素都包含其中。鉴于此，选取水系环度(α指数)、节点连接率(β指数)和水系连通度(γ指数)[7-8,21]来进行结构连通性评价。因此，结构连通性评价方法体现了水系图中点、线之间的相互联系，适用于平原城市河网水系结构连通性评价。

2.1.3水力连通性评价

水系连通性应包括水系格局、结构连通性和水力连通性[2]。水力连通性与结构连通性密切相关，结构连通性是水系连通调控的基础，而水力连通性是水系连通的内在目标，良好的结构连通性有利于河网的规划、修建合理的水利工程，从而提高水力连通性[20]。现有研究往往着重于河网结构的特征变化，而忽略水体流动能力的强弱，故本文在结构连通性基础上，充分考虑水体流动能力对水系连通性的影响，采用流速、水流动势、水位3个指标进行水力连通性评价。其中:流速取河网各河段的平均流速，由于平原城市河网地势平坦、流速平缓，因此在一定程度上可认为河道平均流速越大，河网各河段之间水流置换效果越佳，水力连通性越强[14]；水流动势可反映水体流动能力的强弱[12]，与河道坡降、河道断面形态等有关，坡降决定了水体流速，河道断面形态决定了水体体积；对于不同区域水系的地形、地貌、土壤和气候等都有所差异，因此对于水体流动能力的定量计算方法也就有所差异，而本区域属于平原河网区，地势平坦、流速平缓，水位高低直接反映了各水系的水体流动能力，故采用水位来量化水力连通能力。李景保等[15]用两个水位站点之间的水位差来表征水力连通能力，其计算公式为

(1)

式中：C为同一河流上下游水位站点之间的水力连通能力，m-1；ΔZ为两站点之间的水位差，m。但此方法只能计算一条河流内的上下游水力连通能力，对于整个河网则无法计算。为定量计算平原城市河网的水力连通能力，将该方法进行改进为

(2)

式中：Ch为整个河网各河段的平均水力连通能力，m-1；|ΔZi|为第i条河段上下游站点之间的水位差，m；N为整个河网的河段总数，条。

2.1.4水系连通性评价体系构建

为改善城市水资源短缺等问题，通过比选不同水系连通方案的水系连通效果来确定水系连通最优方案，因此以水系连通最优方案为目标层，以水系格局、结构连通性、水力连通性为准则层，以10项评价指标为指标层，构建水系连通性评价体系见表2。

表2 平原城市河网水系连通性评价体系

2.2 水系连通评价指标计算方法

2.2.1图论法

将河网水系中河流交汇点定义为水系图模型中的节点，将连接节点之间的河流定义为水系图模型中的河链，从而将河网水系概化为由节点和河链共同组成的图形[9]。采用图论法可以获取区域水网河流长度、河流数量、节点数及河链数，从而对结构连通性准则层下各指标进行计算。

2.2.2水动力数学模型

采用水动力数学模型计算水力连通性准则层下各指标。由于研究区域河网复杂，河流实测资料有限，选取与本区域类似、同属海河流域的某小运河段进行模型参数率定，小运河段全衬砌段和非衬砌段糙率分别为0.015和0.025，本模型中大皮营引渠为全衬砌段，故糙率取0.015，其他河段为非衬砌段，糙率取0.025。小运河段设计流量50 m3/s，下游设计水位为31.25 m，以此为边界条件对模型进行验证。小运河段计算水深和设计水深对比见图2，其最大误差0.160 m，均方根误差REMS为6.640%，计算水深和设计水深拟合效果好，该水动力模型可以用于河流水动力数值模拟。模型控制方程为非恒定流Saint-Venant方程组，采用加权四点隐格式有限差分法求解。

图2 小运河段计算水深与设计水深对比

连续性方程

(3)

动量方程

(4)

式中:q1为单位长度侧向入流量，m2/s；Q为流量，m3/s；t为时间，s；v为流速，m/s；x为纵轴坐标，m；g为重力加速度，m/s2；A为过水断面面积，m2；Z为水位，m；Sf=Q|Q|/K2，m3/s；K为流量模数。

2.3 水系连通性评价方法

已有水系连通性评价研究多基于某些指标进行水系连通性评价[8]，而仅通过指标值对水系连通性进行评价缺乏综合性可能存在某一方面指标较优，而另一方面指标较劣的现象。为综合评价不同方案的水系连通性，采用综合评价法对10项指标赋权，进而对不同水系连通方案进行综合评价。

2.3.1指标权重计算

目前，层次分析法和熵权法在确定指标权重时应用较为广泛。层次分析法基于个人定性观点，通过建立层次树模型对各层指标进行相对重要程度的比较，从而确定指标权重，属于主观赋权法[22]。熵权法基于指标数值，定量计算各指标对应的熵值，进而得到各指标对应的熵权，属于客观赋权法[23]。主观赋权法人为因素影响较大，主观性较强，而客观赋权法完全依赖数据自有特征，容易忽略指标特性。为解决主、客观权重计算法存在的问题，在确定评价指标权重时采用AHP-熵综合权重法[24]，权重计算过程如下:

AHP权重计算。计算公式为

(5)

(6)

式中：λmax为判断矩阵的最大特征值；m为判断矩阵的阶数；RI为一致性指标标准值。若CR<0.1，则检验通过。借助MATLAB程序计算λmax对应的特征向量，得到各层次元素权重。将各层次元素权重相乘即可得到评价指标相对准则层的权重，即AHP权重。

熵权计算。首先对评价指标数值进行归一化处理，得到归一化矩阵，然后定量计算各评价指标对应的熵值，得到指标对应的熵权。

指标归一化处理。计算公式为

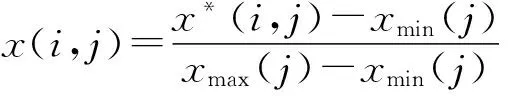
(7)

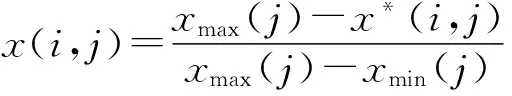
(8)

式中：x(i,j)为第i个评价方案第j个评价指标归一化后的值；xmax(j)和xmin(j)分别为第j个评价指标的最大值和最小值；x*(i,j)为第i个评价方案第j个评价指标的实际值。

熵值计算公式为

(9)

(10)

(11)

式中：Hj为评价指标j的熵值，在此假定当fij=0时，fijlnfij=0；gij为评价指标的归一化矩阵；k为玻尔兹曼常量；N为评价方案的总个数。

熵权计算公式为

(12)

式中：M为评价指标的总个数。

综合权重计算(AHP-熵权法)。将AHP法计算得到的指标权重值记为w*，熵权法计算得到的指标权重记为w′，评价指标的个数记为j(j=1,2,…,M)，计算得出的综合权重

(13)

2.3.2综合评价步骤

通过各方案评价指标数值建立初始决策矩阵X，根据式(14)对矩阵X进行标准化处理得到规范化矩阵Y；由评价指标权重计算结果得到权重矩阵W；通过规范化矩阵Y和权重矩阵W计算得出决策值矩阵V，即V=YW[25-26]。设连通方案有N个，每个待评价方案有M个评价指标，xij代表第i个待评价方案中的第j个指标值，则初始决策矩阵X、规范化矩阵Y、权重矩阵W及决策值矩阵V分别表示为

指标标准化计算公式为

(i=1,2,…,N;j=1,2,…,M)

(14)

2.4 水系连通方案拟定

根据研究区域的相关规划，对污染较严重的胜利支渠、胜丰支渠与小刘庄支渠进行疏通或填埋等改造工程。在3条支渠水流方向为自流的前提下，初拟8种水系连通工况，各工况条件见表3。

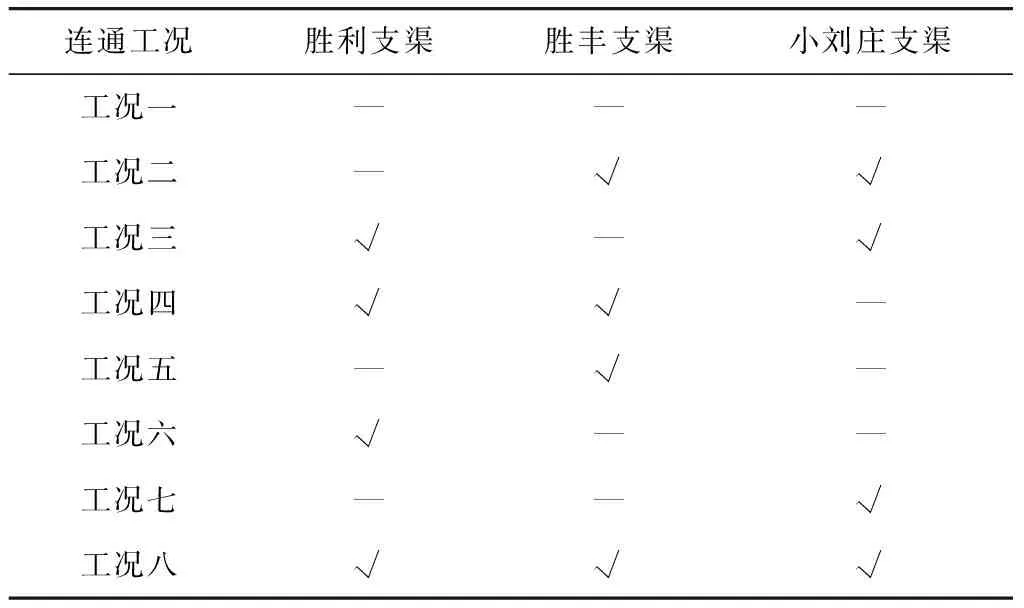
表3 关键支渠不同启闭工况

3 结果与讨论

3.1 水系连通评价指标计算结果

基于GIS平台分别构建8种连通工况的水系图模型，其中工况一的水系模型见图3。采用图论法统计各工况对应河网的河流长度、河流数量、节点数及河链数，对水系格局准则层的河网密度、河频率及结构连通性准则层各指标进行计算。同时，基于研究区域基础数据，对研究区域进行水量平衡分析确定水动力数学模型边界条件，其中工况二水动力模型见图4。在相同流量边界条件下，应用水动力数学模型进行模拟，从而得到各工况河网的水面率及河道槽蓄量，在此基础上进一步统计各河道流速、上下游水位等计算结果并对水力连通性指标进行计算。各工况水系连通性评价指标计算结果见表4。

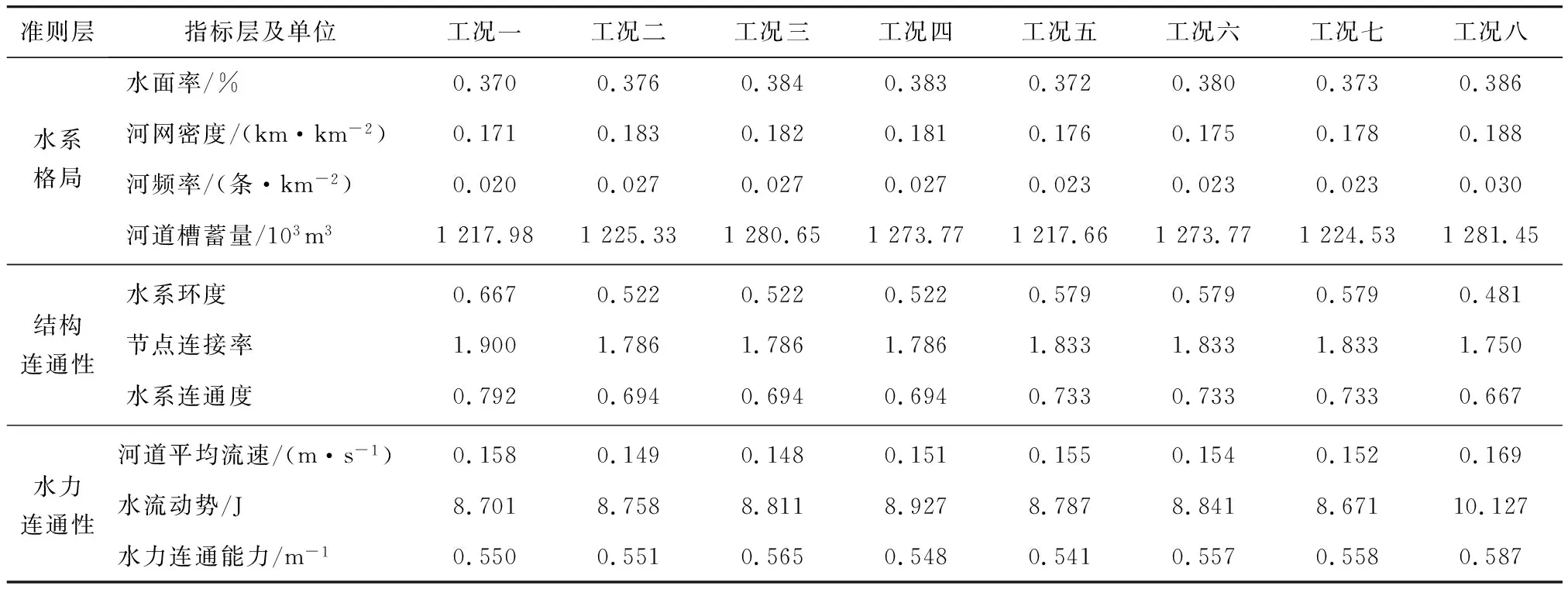
表4 各工况水系连通性评价指标计算结果

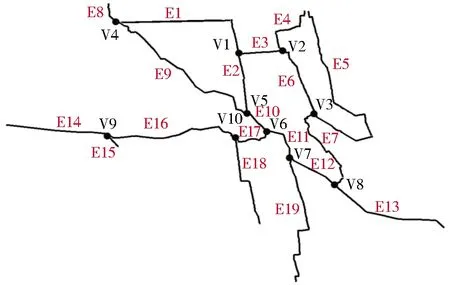
图3 工况一水系模型

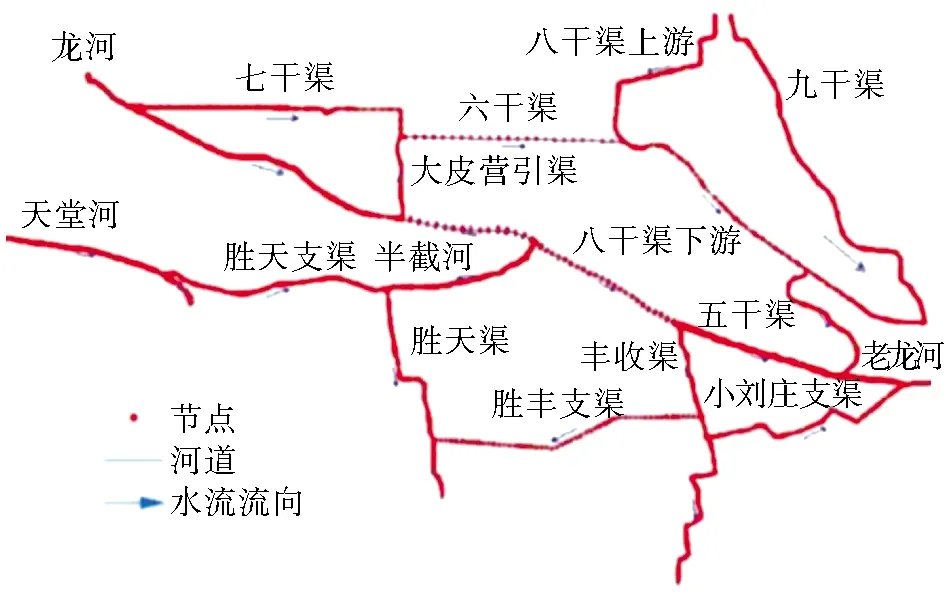
图4 工况二水动力模型

3.2 水系连通方案评价结果

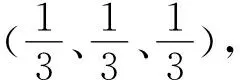
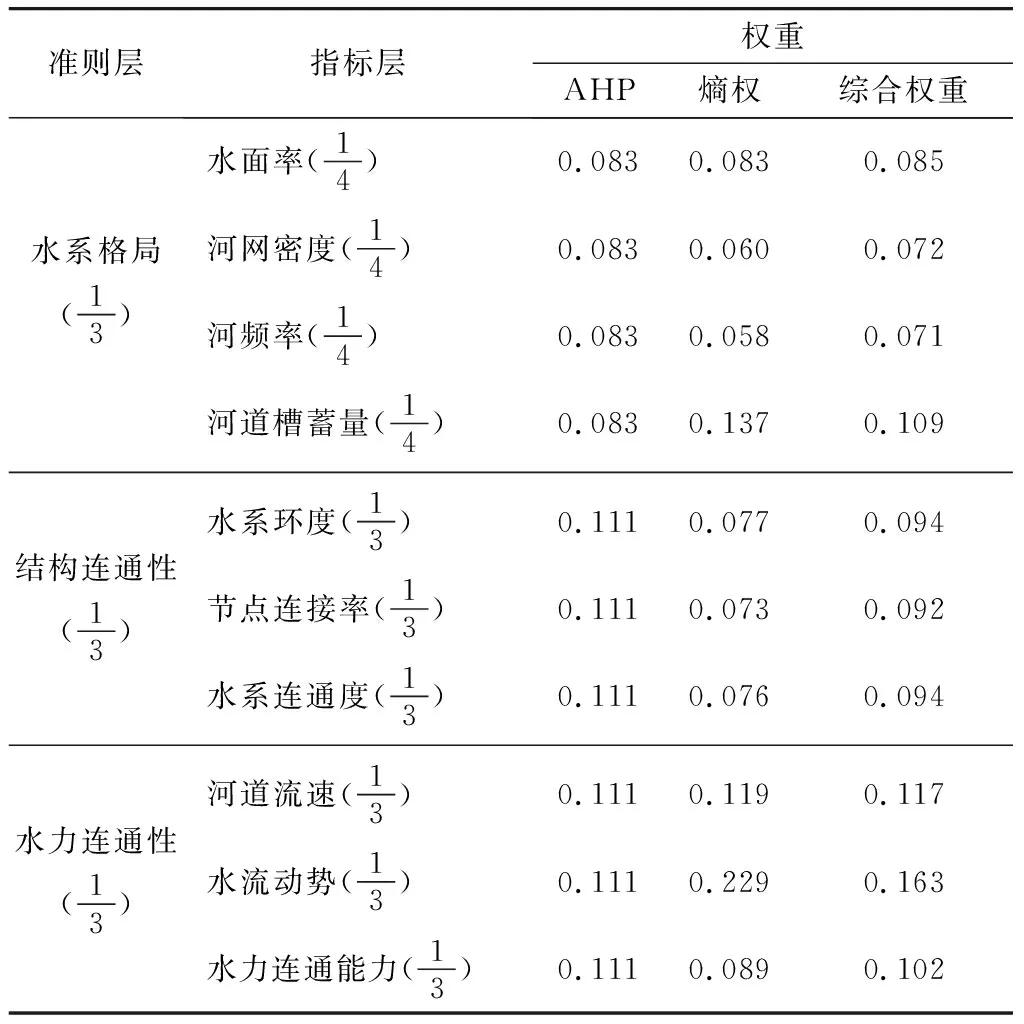
表5 水系连通性评价指标权重计算结果

参考关于水系连通评价指标等级划分的相关研究[21,27-28]，制定适用于本区域的水系连通等级划分标准。根据指标值计算结果将其划分为I～X共10个等级，表示水系连通效果逐渐降低，各指标等级划分标准见表6。将指标等级标准值进行标准化处理，结合评价指标综合权重计算结果，得到适用于本区域的水系连通等级分界线值，其中9项等级分界线值由高到底依次为：0.536、0.527、0.518、0.509、0.500、0.490、0.481、0.472、0.463。对表4指标数值进行标准化处理得到规范化矩阵Y，根据表5得到权重矩阵W，利用规范化矩阵Y、权重矩阵W计算得到决策值矩阵V，见式(15)至(17)。各工况最终的决策值与其对应的评价等级结果见表7。

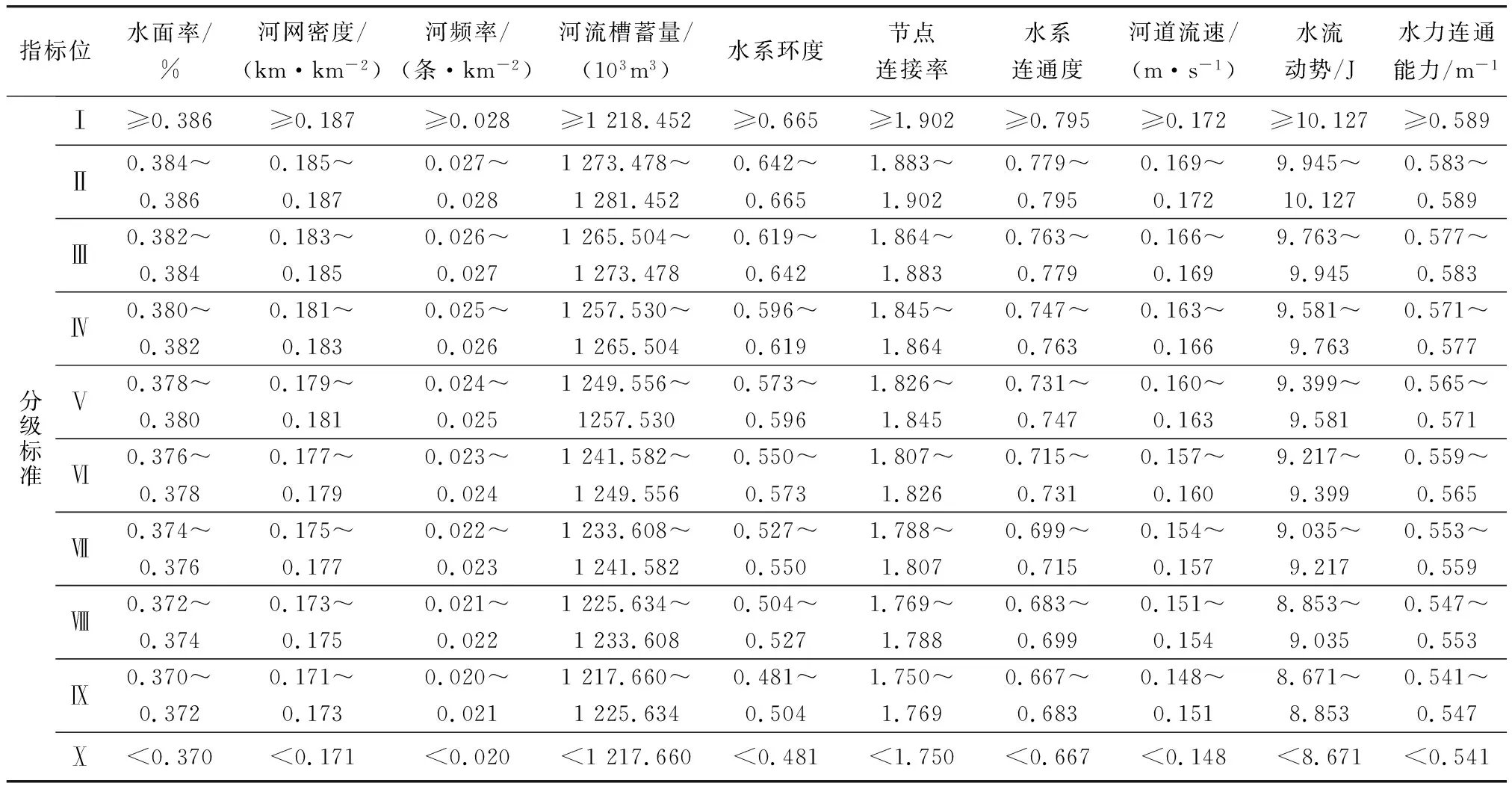
表6 水系连通评价指标体系等级划分标准

表7 各工况决策值与其对应评价等级

Y=(0.490 0.477 0.404 0.487 0.581 0.521 0.543 0.498 0.463 0.488 0.497 0.510 0.532 0.490 0.454 0.489 0.476 0.470 0.466 0.488 0.507 0.508 0.532 0.512 0.454 0.489 0.476 0.467 0.469 0.501 0.506 0.505 0.532 0.510 0.454 0.489 0.503 0.476 0.475 0.486 0.493 0.492 0.468 0.487 0.504 0.502 0.503 0.489 0.467 0.480 0.503 0.490 0.468 0.510 0.504 0.502 0.503 0.486 0.470 0.494 0.494 0.495 0.468 0.490 0.504 0.502 0.503 0.479 0.461 0.495 0.510 0.523 0.596 0.513 0.419 0.479 0.457 0.533 0.539 0.520)T

(15)

W=(0.085 0.072 0.071 0.109 0.094 0.092 0.094 0.117 0.163 0.102)T

(16)

V=YW=(0.495 0.494 0.488 0.488 0.487 0.492 0.487 0.509)T

3.3 最优连通方案分析

对评价体系中水系格局准则层下新增的河道槽蓄量以及水力连通性准则层下改进的水力连通能力两项指标评价结果进行初步分析，利用SPSS软件采用双变量相关分析法分析指标间的相关性，趋势分析结果见图5、图6，相关性分析结果见表8。河道槽蓄量、水力连通能力分别与能反映水系格局和水力连通性的水面率、水流动势变化趋势基本一致，河道槽蓄量与水面率、水力连通能力与水流动势两对指标间的相关系数分别为0.957、0.836，指标间均呈高度相关关系，且显著性系数均小于0.05，表明两对指标间相关关系显著。指标相关性分析结果说明新增的河道槽蓄量和改进的水力连通能力均适用于平原城市河网水系连通性评价体系。

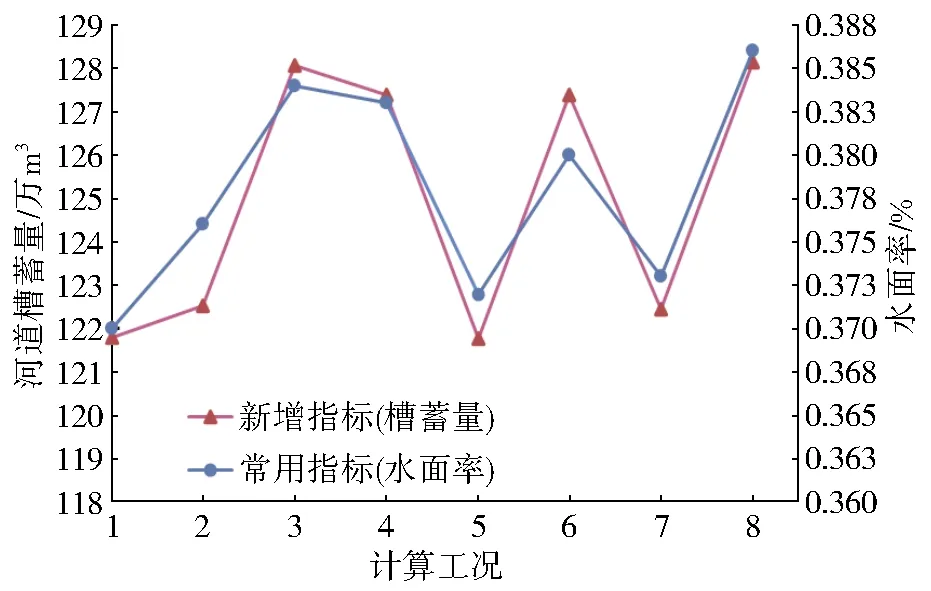
图5 廊坊市水系格局新增指标变化趋势

图6 廊坊市水力连通性改进指标变化趋势

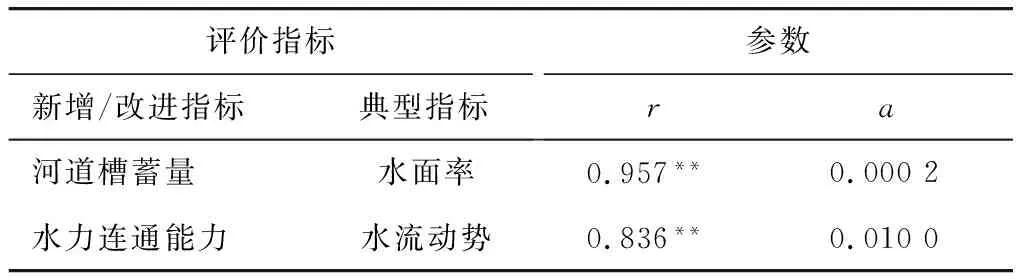
表8 评价指标相关性分析

从水系格局评价结果可以看出：工况八的4项指标均处于最高水平，说明在开启3条支渠后，河网的水系规模最大;其中，河道槽蓄量、水面率分别较关闭3条支渠后提高5.21%、4.32%，河网存储水资源能力增强。表4中结构连通性评价结果表明：工况一在关闭3条支渠后，水系环度、节点连接率、水系连通度最大，分别达到0.667、1.900、0.792，其结构连通性最强；工况八在开启3条支渠后，结构连通性最弱，3项指标分别降低至0.481、1.750、0.667。这是由于结构连通性准则层下指标数值与水系节点数与河链数密切相关，如水系连通度是由水系图的连接河段数与最大可能连接河段数之比计算得到，能够反映河网水系之间连通性强弱和水分输移能力。从结构连通性角度而言，当3条支渠均连通时，水系网状结构相对复杂，在节点增多的同时，其最大可能连接河段数也在增多，导致节点未能充分发挥连接河段的能力。此外，平原城市河网水系人工改造程度高，受人类活动影响显著。新开部分河道后，河流间水流交汇困难，因此结构连通性较差。表4中工况八的河网平均流速最大，为0.169 m3/s，高于其他工况约7%～14.2%，水力连通能力明显增强。其中：水流动势较最低工况提高16.4%，这说明水系连通能够促进河流间的水动力交换，将所有河网支渠进行连通后，水流循环更加通畅，河流间水流置换效果更佳，河网调蓄能力有所增强；同时由于地形等因素影响，连通后的水系具有较好的水动力条件。

由各工况的评价结果可知，不同的工况在水系格局、结构连通性和水力连通性3个准则层均存在差异。以往研究多通过指标值评价方案在某一准则层的连通状况，例如工况一水力连通性较差，但其结构连通性最强，而工况八反之。需要指出的是，并非在所有水系连接的情况下区域河网水系结构连通性最好，而本研究得到的水系连通最优方案其结构连通性也并非最优，这也说明不能仅依靠结构连通性下指标大小决定各方案水系连通情况，需要从多个准则层出发选取相关指标构建河网水系连通性评价体系。因此，为兼顾水系连通性3大准则层，采用综合评价法对各项指标赋权，进而对各工况进行综合评价，结合式(17)中综合评价得分值和等级分界线值可得：工况八得分值为0.509，连通等级为Ⅳ级，连通效果最优；工况五、工况七得分值为0.487，连通等级为Ⅶ级，连通效果最差；其他工况连通等级介于两者之间。可见，由于所有水系连通后河网规模较大，所带来的水系格局与水动力交换优势在一定程度上弥补了水系网状结构复杂造成的结构连通性不足。需要说明，由于区域水系连通目标与关注指标的侧重点不同，在不同研究区域或同一研究区域不同指标赋权结果下，最优连通方案可能会存在差异。

综上，确定工况八为廊坊城区水系连通最优方案，建议河网在输水过程中开启胜利支渠、胜丰支渠和小刘庄支渠，并根据当地实际情况分别对污染严重的3条支渠进行相应的疏通和清淤，以提高整个河网的水系连通性。

4 结 论

围绕平原城市河网水系连通性评价问题，在总结相关研究案例基础上，构建了包含水系格局、结构连通性和水力连通性3大准则层共10项指标的能够反映平原城市河网水系特点的水系连通性评价体系。研究结论如下：

该体系能够较全面地进行平原城市河网水系连通性评价，综合反映不同水系连通方案的水系连通状况。其中水系格局指标反映了城区河网水系的特征，新增的河道槽蓄量与水面率指标间呈显著相关性，其能够较好地反映河网水系存储水资源的能力。

水力连通性指标可反映水系水体流动性，对水力连通性准则层中水力连通能力指标计算方法进行了改进，使其适用于整个河网计算，弥补了以往该项指标只适用于单条河流计算的局限性，但在今后的研究中仍需加强该指标在其他城区水系的应用研究。

针对仅通过指标值评价水系连通状况不能兼顾多因素影响的局限性，基于水系连通性评价体系，采用AHP-熵综合评价法从水系格局、结构连通性和水力连通性3方面对不同水系连通方案进行评价，得到不同水系连通方案的最终评价得分值，以确定水系连通最优方案，并对整个河网提出合理的规划建议。

通过综合评价法确定工况八为廊坊城区水系连通最优方案，即将3条污染严重的河道与其他河道进行连通后河网整体连通效果最优。目前河网内该3条河道已通水，周边水质已有所改善，而本文由于水质资料有限并未对连通前后该区水质情况进行模拟，故今后研究中可进一步分析连通该3条河道后可能会对河网造成的污染扩散风险。