基于降雨时空不确定性的山洪灾害三级预警模式
马细霞,王慧丽,程旭,张溟,肖遥
(1.郑州大学水利科学与工程学院,郑州 450001;2.河南省机场集团有限公司,郑州 450019;3.中水东北勘测设计研究有限责任公司,长春 130021)
山洪灾害指在山区因降雨、融雪等引起的包括洪水、泥石流和滑坡等灾害[1]。受气候和下垫面变化影响,我国山洪灾害频发,严重威胁人民生命财产安全[2]。作为山洪灾害防治重要的非工程措施,山洪预警可预先获取山洪发生的时间、地点和量级等相应灾害信息,进而为组织群众撤离等工作提供决策支持[3-4]。
降雨资料是山洪预警中最重要的信息之一,降雨的时空不确定性严重影响洪峰流量和峰现时间。临界雨量是指导致山洪灾害暴发所对应时段的雨量,是山洪灾害预警的重要指标[5-6]。目前,专家学者针对降雨时空分布的不确定性对临界雨量的影响展开了研究:Yuan等[7]利用概率密度函数表征雨型,分析了不同雨型对临界雨量的影响,结果表明分散雨型的临界雨量明显大于集中雨型的临界雨量;沈天元等[8]以裴河小流域为例,计算流域各种典型雨型的临界雨量,发现不同雨型的临界雨量相差较大;Zhang等[9]评估降雨空间分布变异性,探讨了其对径流模拟的影响,发现随着降雨空间变异性的增加,水文模型的性能降低;闫宝伟等[10]以汉江旬河上游为例,分析了降雨量空间分布与临界雨量的关系,结果表明降雨中心越靠近下游,临界雨量越小。现有研究对临界雨量的计算多侧重于单一的降雨时程分布或者空间分布,缺乏对两种不确定性的综合考虑,而且对于降雨时程分布的随机性和不均匀性的研究较少,同时忽略了总雨量和峰值雨强关系对径流模拟的影响。在山洪灾害临界雨量确定时,考虑降雨不确定性可以获得一系列不同情景下的临界雨量。若将其用于山洪预警,则需逐步查询临界雨量数据集,耗费较多的宝贵时间,不利于快速实时预警,而建立预警模式将会有效简化查询临界雨量的过程。Goodarzi等[11]考虑洪水警报的不确定性因素,基于天气预报模型建立了洪水预警模式。原文林等[12]基于随机雨型的山洪灾害临界雨量计算模型,建立了考虑决策者风险偏好的预警模式。然而,目前综合考虑降雨时空分布不确定性构建山洪预警模式的研究还很少。
针对以上问题,本文在分析流域实测资料的基础上,概化各站点特征雨型,计算风险组合概率的峰量关系,设置降雨空间分布情景,综合考虑降雨时空分布、峰量关系和预警时段等多种不确定性因素,计算不同情景的临界雨量,构建临界雨量数据集合,并建立考虑降雨时空不确定性的三级预警模式,以期为中小流域的山洪预警提供技术参考。研究思路见图1。
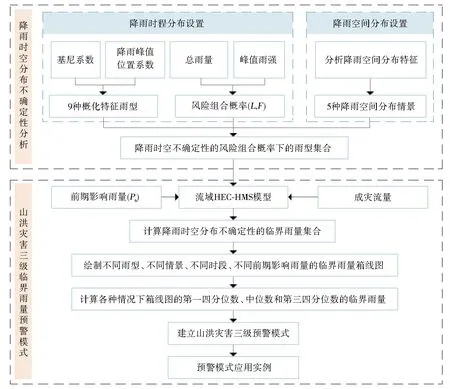
图1 研究思路
1 研究区概况
栾川县栾川流域位于河南省西南部伏牛山区,东经111°11′~112°01′,北纬33°39′~34°11′,属于暖温带大陆性季风气候,年均降水量872.6 mm,多次发生山洪灾害,其中2010年7月22日发生特大暴雨,降雨量超过200 mm,流域内城镇受灾严重,经济损失较大[13]。故选用栾川典型流域为研究区,该流域面积343 km2,河长36.9 km,流域内设有7个雨量监测站及1个水文监测站,各个雨量监测站到流域出口的直线距离见表1。研究区水文监测站及水系情况见图2。
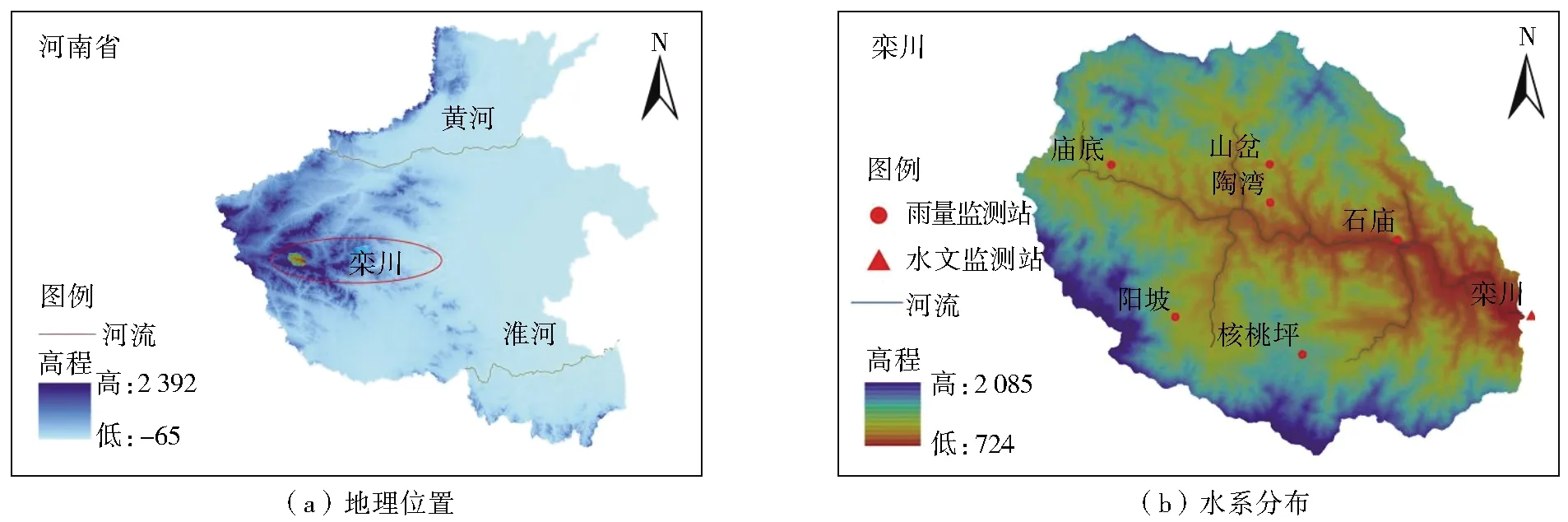
图2 栾川位置及水系分布

表1 雨量监测站到流域出口的直线距离
2 降雨时空分布不确定性
2.1 降雨时程分布设置
2.1.1雨型特征参数
降雨峰值位置对产汇流过程影响显著,采用雨峰位置系数表征降雨雨峰位置[14]。峰值位置系数是指在整场降雨中峰值出现的时段与该场次降雨总历时的比值[15],其计算公式为
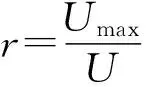
(1)
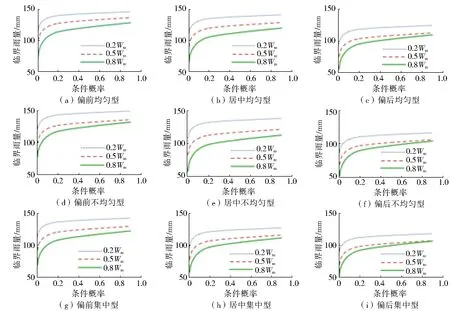
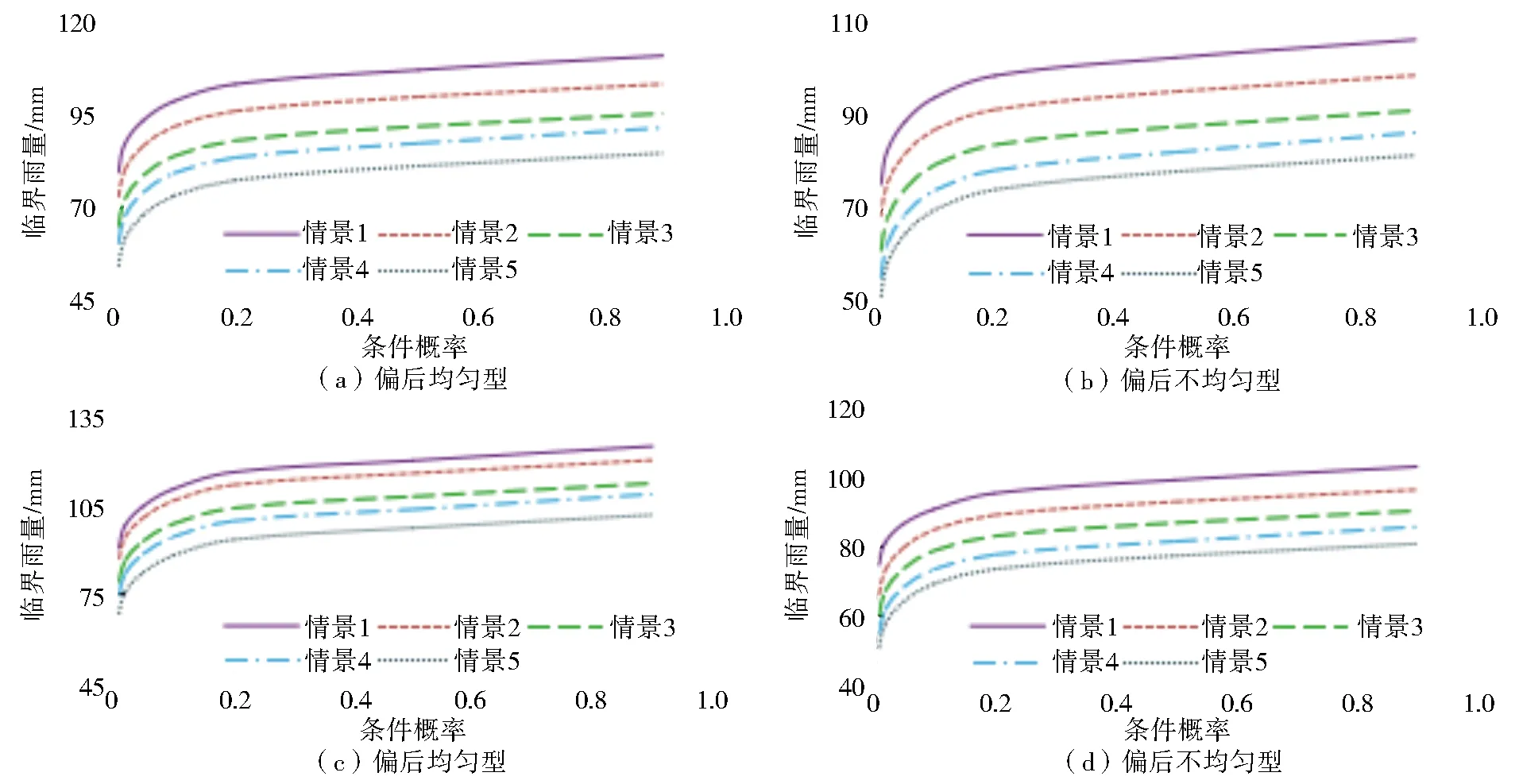
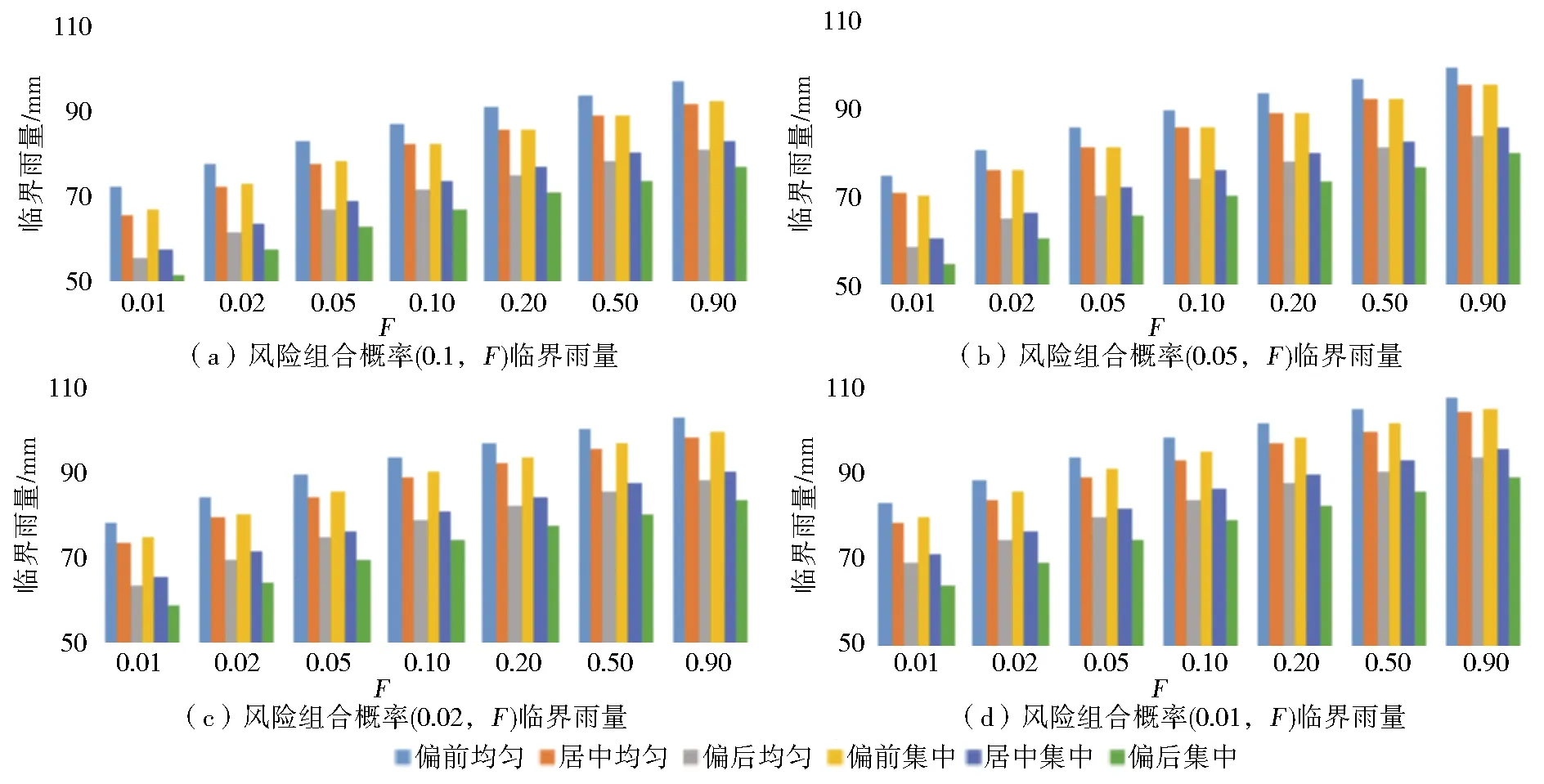
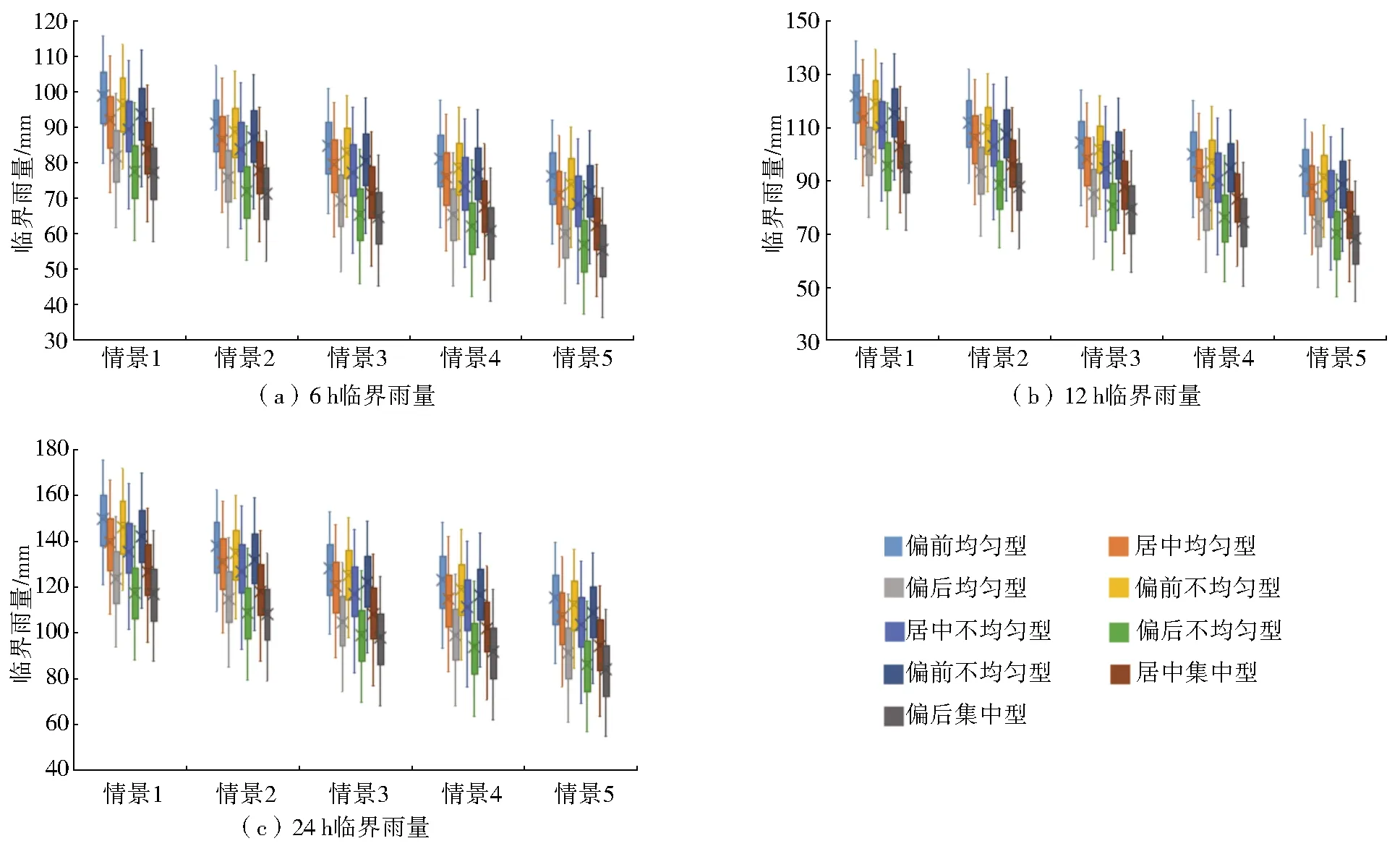
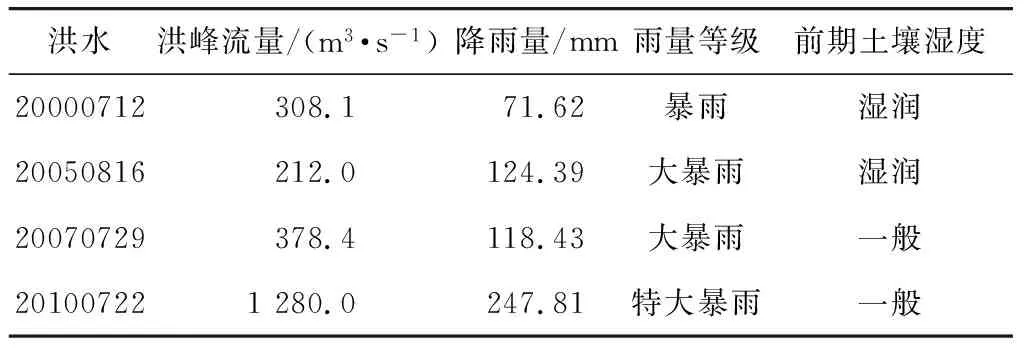
式中:r为雨峰位置系数;Umax为雨峰出现的单位时段,h;U为该场次降雨的总历时,h。根据峰值位置系数可将降雨过程定性划分为偏前(0 为分析降雨时程分布均匀程度对预警指标的影响,采用基于洛伦兹曲线(M)的基尼系数表征降雨时程分布的均匀度。图3为洛伦兹曲线示意图,其中对角线为绝对平均线,纵、横坐标分别为累计降雨百分比和累计时间百分比。基尼系数(G)数学表达式[16]为 图3 洛伦兹曲线 (2) (3) Sa=0.5-Sb,则由上述关系可知 G=1-2Sb (4) 式中:Sa为M与对角线y=x所围成的面积;Sb为M与x轴和x=100%所围成的面积;G∈[0,1],G越接近1,则分配越集中,反之则分配越均匀。 结合雨型实际情况,根据基尼系数将降雨场次划分为均匀型(0.20 2.1.2概化特征雨型 对栾川流域降雨径流资料进行统计分析,将连续最大24 h实际降雨作为雨型分析的资料。根据降雨峰值位置系数和基尼系数将各雨量监测站降雨过程划分为9种类型,把所属类型的降雨场次各时段降雨量的比例取均值作为概化雨型的时段雨量分配比例。以阳坡站概化雨型为例,结果见图4。 图4 阳坡站概化雨型 2.1.3基于Copula函数的峰量关系不确定性分析 在分析雨型对临界雨量影响的研究中,总雨量和峰值雨量的关系往往采用固定的比例,忽视了峰量关系的不确定性。考虑总雨量和峰值雨强的不确定性影响更加契合降雨过程的实际情况[18-19],因此,利用Copula函数构造总雨量和峰值雨强的联合概率分布函数,推求在总雨量一定概率时,多种条件概率下峰值雨强的数值。流域内各雨量监测站总雨量和峰值雨强的条件概率曲线见图5。 图5中的4条线分别代表总雨量重现期T为10、20、50和100 a的条件下峰值雨强对应的条件概率曲线。选取总雨量概率L为0.01、0.02、0.05和0.10,峰值雨强条件概率F为0.01、0.02、0.05、0.10、0.20、0.50和0.90的风险组合概率(L,F)进行峰量关系分析。 图5 各站点Copula函数构建的条件概率分布 假定降雨重心从上游向下游偏移,结合雨量监测站到流域出口的距离,把降雨空间分布设置为情景1至情景5。统计研究区所有场次降雨的7个站点雨量与面雨量的比值,以1.3作为站点降雨比重系数最大值,其他站点根据与降雨重心距离由近到远逐渐减小,最小值设为0.7。不同情景各站点降雨量情况设置见表2。 表2 各站点降雨空间情景设置 对7个站点的9种概化特征雨型、各种风险组合概率的峰量关系以及降雨空间分布情景进行耦合,具体步骤如下:将风险概率组合中的峰值雨强赋值给特征雨型中时程分配比例最大的时段,将总雨量减去峰值雨强的剩余雨量赋值给特征雨型中除了最大比例时段以外的其他时段;计算赋值的各时段雨量占总雨量的百分比,获得各站点降雨的时程分布;按照降雨空间分布情景分配7个雨量监测站的总雨量,即构建了降雨时空分布不确定性的雨型集合。 假设初始时段雨量,根据雨型进行降雨时程分配,将产汇流模型计算的洪峰流量与成灾流量进行对比,若绝对误差满足计算精度要求,此时对应的时段雨量为防灾对象在该预警时段的山洪灾害临界雨量[20]。 HEC-HMS模型是由美国研发的半分布式水文模型,可以根据流域特性选择适宜的模块和计算方法并结合GIS技术推求模型参数,在山丘区有较强的适用性[21]。本文产流、汇流以及河道演算分别采用SCS曲线法、SCS单位线和马斯京根法,该组合原理简单,物理意义明确且参数较少[22-23]。选取1998—2010年降雨和洪水资料作为基础资料,其中10场洪水用于模型参数率定,4场洪水用于模型验证。依据《水文情报预报规范》规定,选用洪量相对误差、洪峰流量相对误差和纳什效率系数3个指标进行评价[24-25]。率定期模拟结果洪峰和径流量合格率均为80%,纳什效率系数合格率为70%,平均合格率为76.67%,精度等级为乙级。验证期模拟结果见表3,结果表明HEC-HMS模型可用于研究区的产汇流计算。 表3 验证期洪水模拟结果统计 选取流域出口附近城关镇大南沟村二组作为防灾对象,其成灾水位747 m,成灾流量83.38 m3/s。综合分析防灾对象所处河段的河谷形态、洪水上涨速率、转移时间和影响人口等因素,确定典型预警时段为6、12和24 h。计算各预警时段不同风险组合概率下9种雨型、5种空间分布情景和3种前期影响雨量Pa情景[干旱,Pa=0.2Wm(Wm为流域最大蓄水量)、一般,Pa=0.5Wm、湿润,Pa=0.8Wm]下的临界雨量。 3.2.1不同雨型对应的临界雨量结果分析 图6展示了降雨空间分布为情景3(降雨重心在中游)、峰量风险组合概率为(0.10,F)、3种前期影响雨量下,不同雨型对应的24 h临界雨量。 图6 各种雨型下的临界雨量 由图6可知,相同前期影响雨量条件,偏前雨型对应的临界雨量比偏后雨型大,均匀雨型对应的临界雨量比集中雨型大。当前期影响雨量为0.2Wm,降雨重心在中游时,偏前均匀雨型比偏后均匀雨型临界雨量大17.52%~23.87%,偏后均匀雨型和偏后集中雨型的临界雨量范围相差5.19%~6.53%。可见,流域降雨时程分布和前期影响雨量对山洪灾害预警影响显著。 3.2.2不同空间分布情景对应的临界雨量结果分析 图7为前期影响雨量为0.5Wm、峰量风险组合概率(0.05,F)的5种降雨空间情景下4种雨型对应的12 h临界雨量。 图7 不同降雨空间分布情景对应的临界雨量 由图7可知,同一个预警对象在不同降雨空间分布情景下,临界雨量差异明显。在风险组合概率(0.05,F)下,情景1对应的临界雨量比情景5大31.61%~48.49%(偏后均匀型)、30.95%~48.84%(偏后不均匀型)、28.39%~44.67%(偏后集中型)、22.77%~32.76%(偏前集中型);当雨型为偏后均匀型时,情景1、情景2、情景3和情景4对应的临界雨量比情景5分别大25.93~26.75 mm、17.87~21.12 mm、10.88~10.98 mm和5.73~5.98 mm。由此可见,降雨空间分布情景不同,其他条件相同时,降雨重心越靠近流域下游,临界雨量就越小,说明流域降雨空间分布对山洪灾害预警影响显著。 3.2.3不同风险组合概率的临界雨量结果分析 图8为前期影响雨量为0.5Wm、降雨空间分布为情景3、不同风险组合概率时6种雨型对应的6 h临界雨量。 由图8可知,在风险组合概率中总雨量的概率L不变时,峰值雨强的条件概率F增大,临界雨量逐渐变大。风险组合概率为(0.10,0.01)偏前集中型的临界雨量为66.85 mm,风险组合概率为(0.10,0.90)偏前集中型的临界雨量为92.02 mm,变化量为25.17 mm,这是因为条件概率F越大意味着峰值雨强越易出现,且其值越小,则在整个降雨时程分配中雨峰的作用被削弱,雨型逐渐变为较均匀的雨型,而均匀型降雨给予流域下垫面较为充足的调蓄时间,导致对应情景的临界雨量变大。 图8 不同风险组合概率下的临界雨量 如上分析,降雨时空分布不确定性对临界雨量影响显著。为此,构建各种不确定条件下临界雨量数据集,用于指导山洪预警。但在具体实施预警过程中,临界雨量数据集数据繁多,查询步骤较多,且实际预警时总雨量重现期和峰值雨强条件概率计算较复杂,为了简化预警过程中查询临界雨量数据集的步骤,将各种情景下不同风险组合概率对应的临界雨量绘制成箱线图。箱线图反映临界雨量数据的分布特征,箱线图下方、中间和上方的线段分别表示第一四分位数(Q1)、中位数(Q2)和第三四分位数(Q3)。 依据临界雨量箱线图特点,将相同前期影响雨量、时空分布情景的临界雨量划分为3个等级:设置Q1为 Ⅰ 级,Q2为 Ⅱ 级,Q3为 Ⅲ 级,构建山洪灾害三级临界雨量预警模式。当临界雨量取Q1时,此时总雨量和峰值雨强的概率均较小,该概率的总雨量和峰值雨强风险组合不易发生,对应的临界雨量比较小,所以在降雨量达到较小的数值时就应该发布预警;当临界雨量取Q3时,此时总雨量和峰值雨强的概率均较大,该概率下的总雨量和峰值雨强风险组合容易发生,对应的临界雨量数值较大,所以在降雨量达到较适中的数值时就应该发布预警。当前期影响雨量为0.5Wm时,临界雨量箱线图见图9。 图9 各预警时段的临界雨量箱线图 基于降雨时空分布不确定性的山洪灾害三级预警模式应用步骤如下: 统计流域内雨量监测站的t时段内的实时降雨数据,并计算降雨开始时的前期影响雨量Pa。 分别计算7个雨量监测站的峰值位置系数和基尼系数,确认降雨雨型。 统计各站点的累计时段降雨总量,判断降雨重心位置。 根据计算的雨型、降雨空间分布情景和前期影响雨量,查询对应雨型、空间分布、前期影响雨量和不同时段的临界雨量数据集,结合天气预报的降雨量级,保守态度的决策者在降雨量达到Q1时发布预警,进取态度的决策者在降雨量达到Q3时发布预警,中立态度的决策者在降雨量达到Q2时发布预警。 以20000712、20050816、20070729和20100722场次降雨为例,进行大南沟村二组山洪灾害预警,详细情况见表4。 表4 场次降雨详细情况 20000712场次的雨型为不均匀偏后型,空间分布为情景4,计算总雨量及峰值雨强,采取进取型态度,发布 Ⅲ 级预警信号,预警信息见图10(a)。滑动比较(t=6、12、24 h)累积雨量与临界雨量线,在7月13日03:00累积雨量超过临界雨量线。根据实测数据可知,该场洪水在7月13日04:00的流量超过成灾流量。 20050816场次的雨型为不均匀偏前型,空间分布为情景2,计算总雨量及峰值雨强,采取进取型态度,发布 Ⅲ 级预警信号。预警信息见图10(b)。滑动比较(t=6、12、24 h)累积雨量与临界雨量线,在8月17日7:00累积雨量超过临界雨量线。根据实测数据可知,该场洪水在8月17日7:00的流量超过成灾流量。 20070729场次的雨型为集中偏后型,降雨空间分布为情景2,计算总雨量及峰值雨强,采取中立型态度,发布 Ⅱ 级预警信号。预警信息见图10(c),滑动比较(t=6、12、24 h)累积雨量与临界雨量线,在7月30日4:00,累积雨量超过临界雨量线。根据实测数据可知,该场洪水在7月30日4:00的流量超过成灾流量。 20100722场次的雨型为不均匀居中型,空间分布为情景4,计算总雨量及峰值雨强,采取保守型态度,发布 Ⅰ 级预警信号,具体预警信息见图10(d)。通过滑动比较(t=6、12、24 h)累积雨量与临界雨量线,在7月24日8:00,累积雨量超过临界雨量线。根据实测数据可知,该场洪水在7月24日10:00的流量超过成灾流量。 图10 场次降雨山洪灾害预警信息 根据山洪灾害三级临界雨量进行预警,四场洪水验证结果均可以在预警对象附近河道内流量达到成灾流量前进行预警,表明所建立的山洪灾害三级临界雨量预警模式效果良好。 以栾川典型流域为研究区,概化了流域特征雨型,构造了基于Copula函数的风险组合概率的峰量关系,设置了降雨重心从上游向下游偏移的降雨空间分布情景,计算了不同情景的临界雨量,探究了降雨时空分布对临界雨量的影响,建立了三级临界雨量预警模式,研究结论如下: 根据基尼系数和峰值雨强位置系数将各站点的实际降雨过程分别概化成了9种特征雨型,基于水文数据的统计特征和Copula函数特性计算了不同风险组合概率的峰量关系,并设置了5种降雨空间分布情景,可有效地表征流域的降雨时空不确定性。 当前期影响雨量为0.2Wm,降雨重心在中游时,偏前均匀雨型比偏后均匀雨型临界雨量大17.52%~23.87%,偏后均匀雨型和偏后集中雨型的临界雨量范围相差5.19%~6.53%,说明雨型对临界雨量影响显著,降雨时程分布越不均匀,雨峰越偏后,临界雨量越小;前期影响雨量为0.5Wm时,在情景1时12 h临界雨量比情景5大31.61%~48.84%,表明降雨中心越靠近下游,临界雨量越小;前期影响雨量为0.5Wm,风险组合概率为(0.10,0.01)对应的临界雨量与风险组合概率为(0.10,0.90)的差值可达25.17 mm,说明在风险组合概率中总雨量概率不变时,峰值雨强条件概率越大,临界雨量逐渐越大。可见不同降雨时空分布情景的临界雨量值相差较大。 构建临界雨量数据集,建立了考虑降雨时空分布不确定性的三级临界雨量预警模式,并以20000712、20050816、20070729、20100722场次降雨为例进行验证,结果表明根据山洪灾害三级临界雨量进行预警,可在预警对象附近河道流量达到成灾流量前进行预警,考虑降雨时空分布不确定性的三级预警模式合理可靠,可为其他中小流域的山洪预警提供技术参考。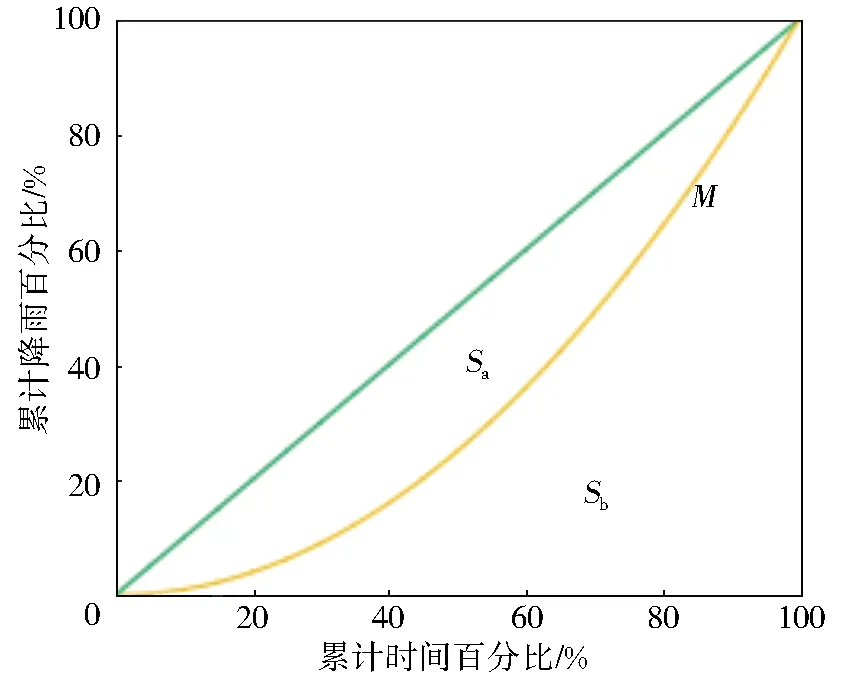


2.2 降雨空间分布设置
3 临界雨量计算及结果分析
3.1 临界雨量计算
3.2 降雨时空不确定性对临界雨量影响分析
4 山洪灾害三级临界雨量预警模式
4.1 预警模式构建
4.2 预警模式应用实例

5 结 论

